2024人教版数学九年级下学期课时练--专项素养综合全练(二)反比例函数中k的几何意义(含解析)
文档属性
| 名称 | 2024人教版数学九年级下学期课时练--专项素养综合全练(二)反比例函数中k的几何意义(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 499.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 09:37:22 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024人教版数学九年级下学期
专项素养综合全练(二)
反比例函数中k的几何意义
类型一 一个象限内运用k的几何意义
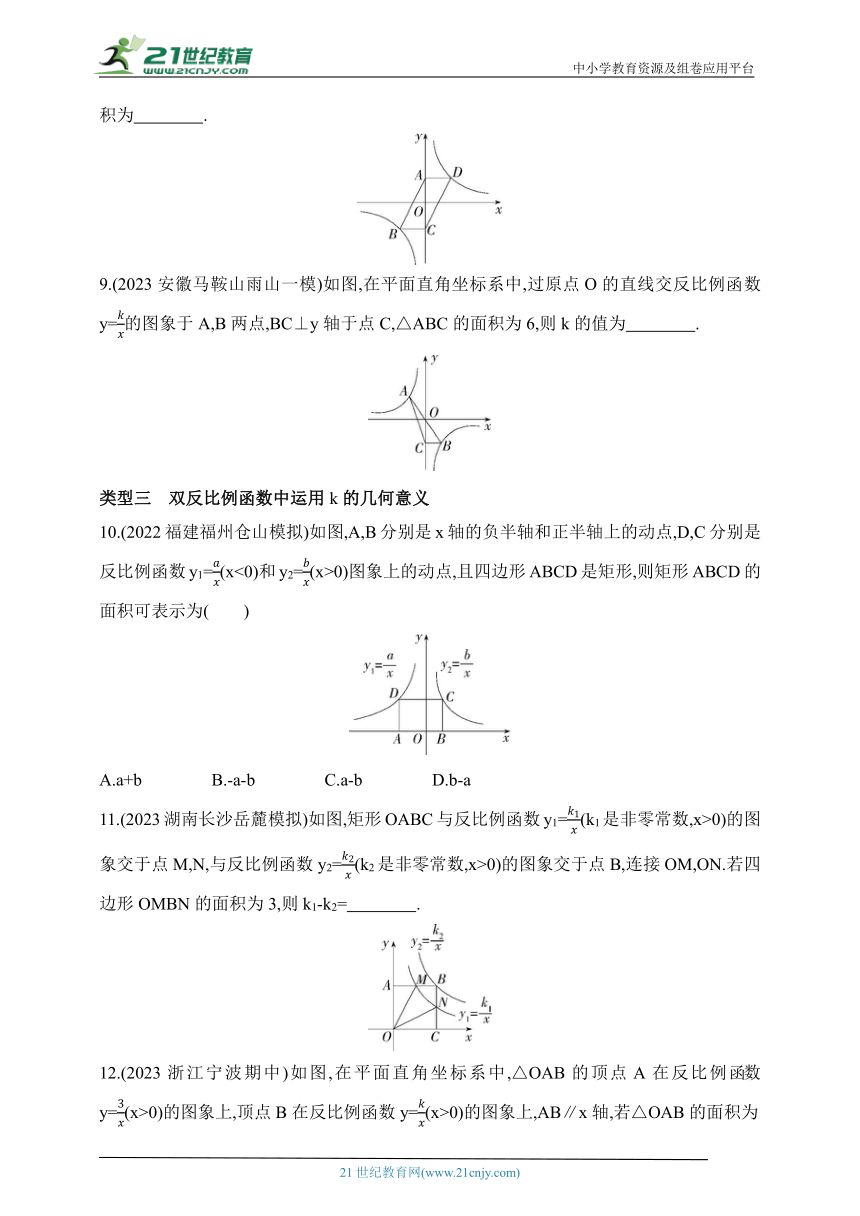
1.(2023河北保定莲池期末)如图,点P是反比例函数y=(x>0)的图象上的任意一点,过点P分别作两坐标轴的垂线,与坐标轴构成矩形OAPB,点D是矩形OAPB内任意一点,连接DA,DB,DP,DO,则图中阴影部分的面积是( )
A.1 B.2 C.3 D.4
2.【等积变换求面积】(2022安徽合肥庐阳模拟)如图,点A在反比例函数y=(k≠0)的图象上,点C在x轴的正半轴上,AC交y轴于点B,若点B是AC中点,△AOB的面积为1,则k的值为( )
A.-2 B.-3 C.-4 D.-6
3.(2023湖南益阳南县月考)如图, OABC的边OA在x轴上,顶点C在反比例函数y=-(x<0)的图象上,BC与y轴相交于点D,且D为BC的中点,则 OABC的面积为 .
4.(2023广东深圳龙岗二模)如图,四边形OABC是面积为4的菱形,∠ABC=60°,点C在y轴正半轴上,若反比例函数y=(x>0)的图象经过点B,则k= .
5.(2023浙江绍兴中考)如图,在平面直角坐标系xOy中,函数y=(k为大于0的常数,x>0)图象上的两点A(x1,y1),B(x2,y2)满足x2=2x1,△ABC的边AC∥x轴,边BC∥y轴,若△OAB的面积为6,则△ABC的面积是 .
类型二 两个象限内运用k的几何意义
6.(2022辽宁沈阳和平期末)如图,点P,点Q都在反比例函数y=的图象上,过点P分别作x轴、y轴的垂线,两条垂线与两坐标轴围成的矩形面积为S1,过点Q作x轴的垂线,交x轴于点A,△OAQ的面积为S2,若S1+S2=3,则k的值为( )
A.2 B.1
C.-1 D.-2
7.【和差法求面积】(2023山东济宁汶上期末)如图,点P(m,1),点Q(-2,n)都在反比例函数y=的图象上.过点P分别向x轴,y轴作垂线,垂足分别为点M,N.连接OP,OQ,PQ.若四边形OMPN的面积记作S1,△POQ的面积记作S2,则( )
A.S1∶S2=2∶3 B.S1∶S2=1∶1
C.S1∶S2=4∶1 D.S1∶S2=4∶3
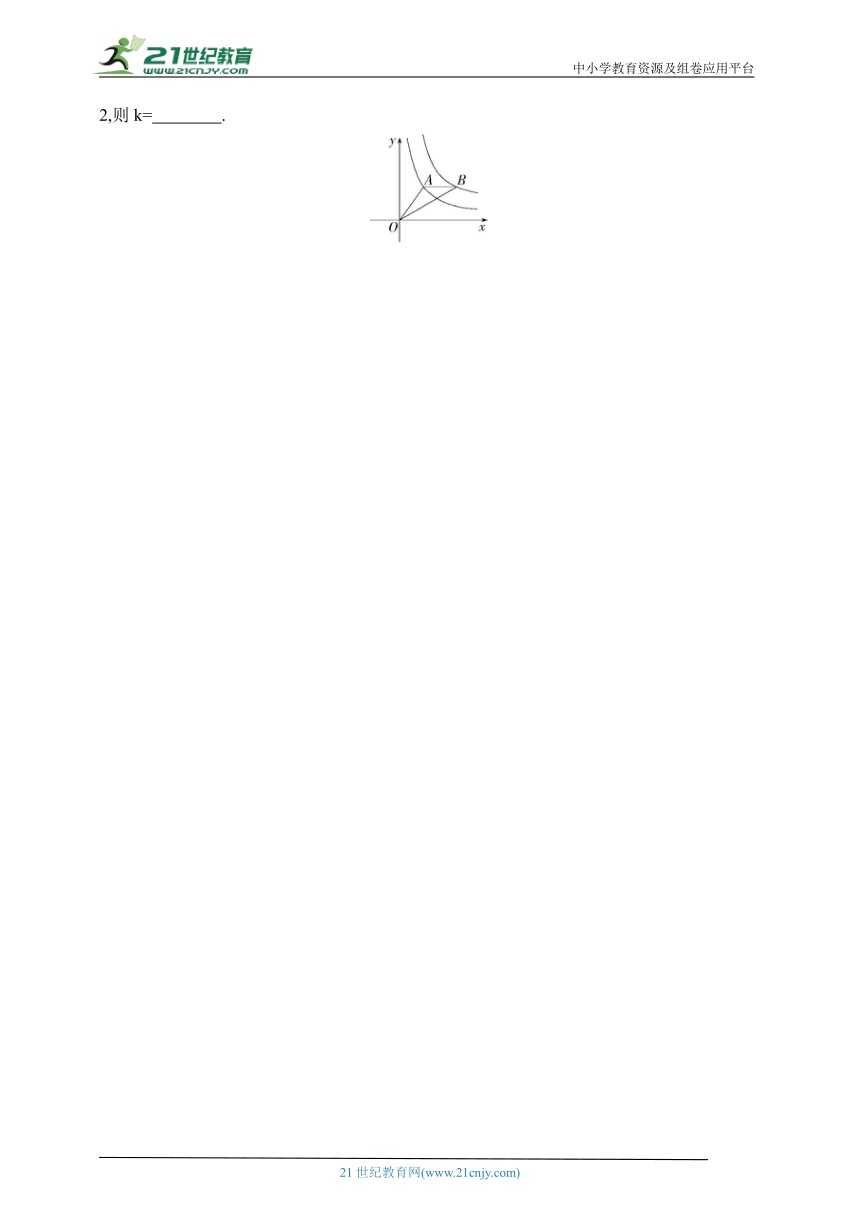
8.【转化与化归思想】(2022江苏南京鼓楼期末)如图, ABCD的对角线AC在y轴上,原点O为AC的中点,点D在第一象限内,AD∥x轴,当双曲线y=经过点D时, ABCD的面积为 .
9.(2023安徽马鞍山雨山一模)如图,在平面直角坐标系中,过原点O的直线交反比例函数y=的图象于A,B两点,BC⊥y轴于点C,△ABC的面积为6,则k的值为 .
类型三 双反比例函数中运用k的几何意义
10.(2022福建福州仓山模拟)如图,A,B分别是x轴的负半轴和正半轴上的动点,D,C分别是反比例函数y1=(x<0)和y2=(x>0)图象上的动点,且四边形ABCD是矩形,则矩形ABCD的面积可表示为( )
A.a+b B.-a-b C.a-b D.b-a
11.(2023湖南长沙岳麓模拟)如图,矩形OABC与反比例函数y1=(k1是非零常数,x>0)的图象交于点M,N,与反比例函数y2=(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1-k2= .
12.(2023浙江宁波期中)如图,在平面直角坐标系中,△OAB的顶点A在反比例函数y=(x>0)的图象上,顶点B在反比例函数y=(x>0)的图象上,AB∥x轴,若△OAB的面积为2,则k= .
答案全解全析
1.B ∵点D是矩形OAPB内任意一点,∴S阴影=S矩形OAPB=×|4|=2.故选B.
2.C 如图,过点A作AD⊥y轴于D,∴∠ADB=∠BOC=90°,在△ADB和△COB中,∴△ADB≌△COB(AAS),∴BD=OB,∴S△ABD=S△AOB=1,∴S△AOD=2=|k|,∴|k|=4,∵k<0,∴k=-4.故选C.
方法解读 等积变换求面积:图形面积不易求出时,可依据“全等三角形的面积相等”“等底等高的三角形的面积相等”等,转化为求另一个图形的面积.
3.8
解析 如图,连接OB,∵四边形OABC是平行四边形,∴BC∥OA,∴BC⊥y轴,∴S△COD=×|-4|=2,∵D为BC的中点,∴S△BOC=2S△COD=4,∴S OABC=2S△BOC=8.
4.6
解析 如图,连接OB,延长BA交x轴于D,∵BD∥OC,∴BD⊥x轴.∵四边形OABC为菱形,∠ABC=60°,∴∠AOC=60°,∴∠AOD=30°,∴AO=AB=2AD,∴AD∶AB=1∶2,∵S菱形OABC=4,∴S△AOB=2,∴S△OAD=1,∴S△OBD=3,∴=3,∴k=±6.∵反比例函数的图象位于第一象限,∴k=6.
5.2
解析 如图,延长CA交y轴于点E,延长CB交x轴于点F,∴CE⊥y轴,CF⊥x轴,∴四边形OECF为矩形,∵x2=2x1,∴点A为CE的中点,由k的几何意义得S△OAE=S△OBF,又OF=2AE,∴OE=2BF,∴点B为CF的中点,∴S△OAB=S矩形-S△AEO-S△BOF-S△ABC=S矩形-S矩形-S矩形-S矩形=S矩形=6,∴S矩形=16,∴S△ABC=×16=2.
6.D 由题意得S1=|k|,S2=|k|,则|k|+|k|=3,解得|k|=2,∵反比例函数的图象在第二、四象限,∴k<0,∴k=-2.故选D.
7.D ∵点P(m,1),点Q(-2,n)都在反比例函数y=的图象上,∴S1=|k|=4,m×1=-2n=4,∴m=4,n=-2,∴P(4,1),Q(-2,-2).如图,作QK⊥PN,交PN的延长线于K,∵PN=4,ON=1,KN=2,PK=6,KQ=3,∴S2=S△PQK-S△PON-S梯形ONKQ=×(1+3)×2=3,∴S1∶S2=4∶3.故选D.
8.8
解析 连接OD(图略),∵双曲线y=经过点D,AD∥x轴,∴S△AOD=|k|=2.
∵O为AC的中点,∴S ABCD=2S△ACD=4S△AOD=8.
9.-6
解析 由对称性可知,OA=OB,∴S△AOC=S△BOC=S△ABC.∵BC⊥y轴,△ABC的面积为6,∴S△BOC=S△ABC=|k|,∵反比例函数的图象位于第二、四象限,∴k<0,∴k=-6.
10.D 如图,记CD与y轴的交点为点E,∵四边形ABCD是矩形,∴四边形AOED和四边形BCEO为矩形,∵点C和点D分别在反比例函数y2=(x>0)和y1=(x<0)的图象上,∴S矩形AOED=|a|=-a,S矩形BCEO=|b|=b,∴S矩形ABCD=S矩形AOED+S矩形BCEO=b-a.故选D.
11.-3
解析 ∵反比例函数y1=(x>0)与y2=(x>0)的图象均在第一象限,∴k1>0,k2>0.∵点M,N均在反比例函数y1=的图象上,∴S△OAM=S△OCN=k1,∵矩形OABC的顶点B在反比例函数y2=的图象上,∴S矩形OABC=k2,∵S四边形OMBN=S矩形OABC-S△OAM-S△OCN=3,∴k2-k1=3,∴k1-k2=-3.
12.7
解析 如图,延长BA交y轴于点M,过点B作BN⊥x轴于点N,AD⊥x轴于点D,∵△OAB的顶点A在反比例函数y=(x>0)的图象上,顶点B在反比例函数y=(x>0)的图象上,∴S矩形BMON=|k|,S矩形ADOM=3,∴S矩形ADNB=|k|-3=2S△OAB=4,∴|k|=7.∵k>0,∴k=7.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版数学九年级下学期
专项素养综合全练(二)
反比例函数中k的几何意义
类型一 一个象限内运用k的几何意义
1.(2023河北保定莲池期末)如图,点P是反比例函数y=(x>0)的图象上的任意一点,过点P分别作两坐标轴的垂线,与坐标轴构成矩形OAPB,点D是矩形OAPB内任意一点,连接DA,DB,DP,DO,则图中阴影部分的面积是( )
A.1 B.2 C.3 D.4
2.【等积变换求面积】(2022安徽合肥庐阳模拟)如图,点A在反比例函数y=(k≠0)的图象上,点C在x轴的正半轴上,AC交y轴于点B,若点B是AC中点,△AOB的面积为1,则k的值为( )
A.-2 B.-3 C.-4 D.-6
3.(2023湖南益阳南县月考)如图, OABC的边OA在x轴上,顶点C在反比例函数y=-(x<0)的图象上,BC与y轴相交于点D,且D为BC的中点,则 OABC的面积为 .
4.(2023广东深圳龙岗二模)如图,四边形OABC是面积为4的菱形,∠ABC=60°,点C在y轴正半轴上,若反比例函数y=(x>0)的图象经过点B,则k= .
5.(2023浙江绍兴中考)如图,在平面直角坐标系xOy中,函数y=(k为大于0的常数,x>0)图象上的两点A(x1,y1),B(x2,y2)满足x2=2x1,△ABC的边AC∥x轴,边BC∥y轴,若△OAB的面积为6,则△ABC的面积是 .
类型二 两个象限内运用k的几何意义
6.(2022辽宁沈阳和平期末)如图,点P,点Q都在反比例函数y=的图象上,过点P分别作x轴、y轴的垂线,两条垂线与两坐标轴围成的矩形面积为S1,过点Q作x轴的垂线,交x轴于点A,△OAQ的面积为S2,若S1+S2=3,则k的值为( )
A.2 B.1
C.-1 D.-2
7.【和差法求面积】(2023山东济宁汶上期末)如图,点P(m,1),点Q(-2,n)都在反比例函数y=的图象上.过点P分别向x轴,y轴作垂线,垂足分别为点M,N.连接OP,OQ,PQ.若四边形OMPN的面积记作S1,△POQ的面积记作S2,则( )
A.S1∶S2=2∶3 B.S1∶S2=1∶1
C.S1∶S2=4∶1 D.S1∶S2=4∶3
8.【转化与化归思想】(2022江苏南京鼓楼期末)如图, ABCD的对角线AC在y轴上,原点O为AC的中点,点D在第一象限内,AD∥x轴,当双曲线y=经过点D时, ABCD的面积为 .
9.(2023安徽马鞍山雨山一模)如图,在平面直角坐标系中,过原点O的直线交反比例函数y=的图象于A,B两点,BC⊥y轴于点C,△ABC的面积为6,则k的值为 .
类型三 双反比例函数中运用k的几何意义
10.(2022福建福州仓山模拟)如图,A,B分别是x轴的负半轴和正半轴上的动点,D,C分别是反比例函数y1=(x<0)和y2=(x>0)图象上的动点,且四边形ABCD是矩形,则矩形ABCD的面积可表示为( )
A.a+b B.-a-b C.a-b D.b-a
11.(2023湖南长沙岳麓模拟)如图,矩形OABC与反比例函数y1=(k1是非零常数,x>0)的图象交于点M,N,与反比例函数y2=(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1-k2= .
12.(2023浙江宁波期中)如图,在平面直角坐标系中,△OAB的顶点A在反比例函数y=(x>0)的图象上,顶点B在反比例函数y=(x>0)的图象上,AB∥x轴,若△OAB的面积为2,则k= .
答案全解全析
1.B ∵点D是矩形OAPB内任意一点,∴S阴影=S矩形OAPB=×|4|=2.故选B.
2.C 如图,过点A作AD⊥y轴于D,∴∠ADB=∠BOC=90°,在△ADB和△COB中,∴△ADB≌△COB(AAS),∴BD=OB,∴S△ABD=S△AOB=1,∴S△AOD=2=|k|,∴|k|=4,∵k<0,∴k=-4.故选C.
方法解读 等积变换求面积:图形面积不易求出时,可依据“全等三角形的面积相等”“等底等高的三角形的面积相等”等,转化为求另一个图形的面积.
3.8
解析 如图,连接OB,∵四边形OABC是平行四边形,∴BC∥OA,∴BC⊥y轴,∴S△COD=×|-4|=2,∵D为BC的中点,∴S△BOC=2S△COD=4,∴S OABC=2S△BOC=8.
4.6
解析 如图,连接OB,延长BA交x轴于D,∵BD∥OC,∴BD⊥x轴.∵四边形OABC为菱形,∠ABC=60°,∴∠AOC=60°,∴∠AOD=30°,∴AO=AB=2AD,∴AD∶AB=1∶2,∵S菱形OABC=4,∴S△AOB=2,∴S△OAD=1,∴S△OBD=3,∴=3,∴k=±6.∵反比例函数的图象位于第一象限,∴k=6.
5.2
解析 如图,延长CA交y轴于点E,延长CB交x轴于点F,∴CE⊥y轴,CF⊥x轴,∴四边形OECF为矩形,∵x2=2x1,∴点A为CE的中点,由k的几何意义得S△OAE=S△OBF,又OF=2AE,∴OE=2BF,∴点B为CF的中点,∴S△OAB=S矩形-S△AEO-S△BOF-S△ABC=S矩形-S矩形-S矩形-S矩形=S矩形=6,∴S矩形=16,∴S△ABC=×16=2.
6.D 由题意得S1=|k|,S2=|k|,则|k|+|k|=3,解得|k|=2,∵反比例函数的图象在第二、四象限,∴k<0,∴k=-2.故选D.
7.D ∵点P(m,1),点Q(-2,n)都在反比例函数y=的图象上,∴S1=|k|=4,m×1=-2n=4,∴m=4,n=-2,∴P(4,1),Q(-2,-2).如图,作QK⊥PN,交PN的延长线于K,∵PN=4,ON=1,KN=2,PK=6,KQ=3,∴S2=S△PQK-S△PON-S梯形ONKQ=×(1+3)×2=3,∴S1∶S2=4∶3.故选D.
8.8
解析 连接OD(图略),∵双曲线y=经过点D,AD∥x轴,∴S△AOD=|k|=2.
∵O为AC的中点,∴S ABCD=2S△ACD=4S△AOD=8.
9.-6
解析 由对称性可知,OA=OB,∴S△AOC=S△BOC=S△ABC.∵BC⊥y轴,△ABC的面积为6,∴S△BOC=S△ABC=|k|,∵反比例函数的图象位于第二、四象限,∴k<0,∴k=-6.
10.D 如图,记CD与y轴的交点为点E,∵四边形ABCD是矩形,∴四边形AOED和四边形BCEO为矩形,∵点C和点D分别在反比例函数y2=(x>0)和y1=(x<0)的图象上,∴S矩形AOED=|a|=-a,S矩形BCEO=|b|=b,∴S矩形ABCD=S矩形AOED+S矩形BCEO=b-a.故选D.
11.-3
解析 ∵反比例函数y1=(x>0)与y2=(x>0)的图象均在第一象限,∴k1>0,k2>0.∵点M,N均在反比例函数y1=的图象上,∴S△OAM=S△OCN=k1,∵矩形OABC的顶点B在反比例函数y2=的图象上,∴S矩形OABC=k2,∵S四边形OMBN=S矩形OABC-S△OAM-S△OCN=3,∴k2-k1=3,∴k1-k2=-3.
12.7
解析 如图,延长BA交y轴于点M,过点B作BN⊥x轴于点N,AD⊥x轴于点D,∵△OAB的顶点A在反比例函数y=(x>0)的图象上,顶点B在反比例函数y=(x>0)的图象上,∴S矩形BMON=|k|,S矩形ADOM=3,∴S矩形ADNB=|k|-3=2S△OAB=4,∴|k|=7.∵k>0,∴k=7.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
