2024人教版数学九年级下学期课时练--专项素养综合全练(六)解直角三角形实际应用的常见类型(含解析)
文档属性
| 名称 | 2024人教版数学九年级下学期课时练--专项素养综合全练(六)解直角三角形实际应用的常见类型(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 472.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 09:38:40 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024人教版数学九年级下学期
专项素养综合全练(六)
解直角三角形实际应用的常见类型
类型一 解一个直角三角形
1.(2023山东泰安东平二模)
某驱逐舰在海上执行任务后刚返回到港口A,接到上级指令,发现在其北偏东30°方向上有一艘可疑船只C,与此同时在港口A北偏东60°方向上且距离10 km处有另一艘驱逐舰B也收到了相关指令,驱逐舰B恰好在可疑船只C的南偏东30°方向上,则可疑船只C与港口A之间的距离为( )
A. km B. km
C. km D.10 km
2.【新素材】(2022广东深圳龙华二模)如图,一名患者体内某重要器官后面有一肿瘤在A处.在接受放射性治疗时,为了最大限度地保证疗效,并且防止伤害器官,射线必须从侧面照射肿瘤.已知射线从肿瘤右侧10 cm的B处进入身体,且射线与皮肤所成的夹角∠CBA=32.7°,则肿瘤在皮下的深度AC约为 cm.(参考数据:sin 32.7°≈0.54,cos 32.7°≈0.84,tan 32.7°≈0.64)
3.(2022湖北襄阳襄城模拟)如图,沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工.从AC上的一点B取∠ABD=140°,沿BD方向前进,取∠BDE=50°,测得BD=520 m,BC=80 m,使A、C、E三点在同一直线上,求公路CE段的长度.(结果保留小数点后一位)(参考数据:sin 50°≈0.77,cos 50°≈0.64,tan 50°≈1.19)
类型二 “背靠背”型
4.(2023山西太原杏花岭模拟)如图,从热气球C上测得两建筑物底部A、B的俯角分别为29.5°和45°,如果这时热气球的高度CD为100米,且点A、D、B在同一直线上,则A、B之间的距离为 .(结果精确到1米)(参考数据:sin 29.5°≈0.49,cos 29.5°≈0.87,tan 29.5°≈0.57)
5.(2023湖北武汉武昌一模)A,B两市相距150 km,分别从A,B处测得某风景区中心C处的方向角如图所示,tan α=1.627,tan β=1.373.已知风景区是以C为圆心,r为半径的圆形区域.为了开发旅游,有关部门设计、修建连接A,B两市的高速公路,则r= km时,高速公路正好经过风景区的边界.
6.(2023山东菏泽中考)无人机在实际生活中的应用越来越广泛.如图所示,某人利用无人机测量大楼的高度BC,无人机在空中点P处,测得点P距地面上的点A 80米,点A处的俯角为60°,楼顶点C处的俯角为30°,已知点A与大楼的距离AB为70米(点A,B,C,P在同一平面内),求大楼的高度BC(结果保留根号).
类型三 “母子”型
7.(2023广西贵港平南模拟)明珠塔是一栋古代工艺与现代工艺完美融合的中式建筑.数学活动课上,老师带领兴趣小组去测量明珠塔的高度.如图,在C处用高0.5米的仪器CE测得塔顶A的仰角为30°,向塔的方向前进46米到达D处,此时测得塔顶A的仰角为60°,则明珠塔的高AB为 米(结果保留根号).
类型四 “拥抱”型
8.【国防科技】(2023湖北武汉江汉模拟)
如图,一枚火箭从地面O处成功发射,当火箭到达点A处时,地面D处的雷达站测得AD=4 000米,仰角为30°,3秒后,火箭竖直上升到达点B处,此时地面C处的雷达站测得B处的仰角为45°.已知点O,C,D在同一直线上,C,D两处相距460米,则火箭从A处上升到B处的平均速度为 米/秒.(结果精确到1米/秒;参考数据:≈1.732,≈1.414)
9.(2022山东烟台牟平一模)如图,一名高山滑雪运动员沿着斜坡FC滑行,他在点D处测得大树顶端A的仰角为30°,从D点再滑行2 米到达坡底的C点,在点C处测得大树顶端A的仰角为45°,若斜坡CF的坡比i=1∶3(点E,C,B在同一水平线上),则大树的高度AB为
米(结果保留根号).
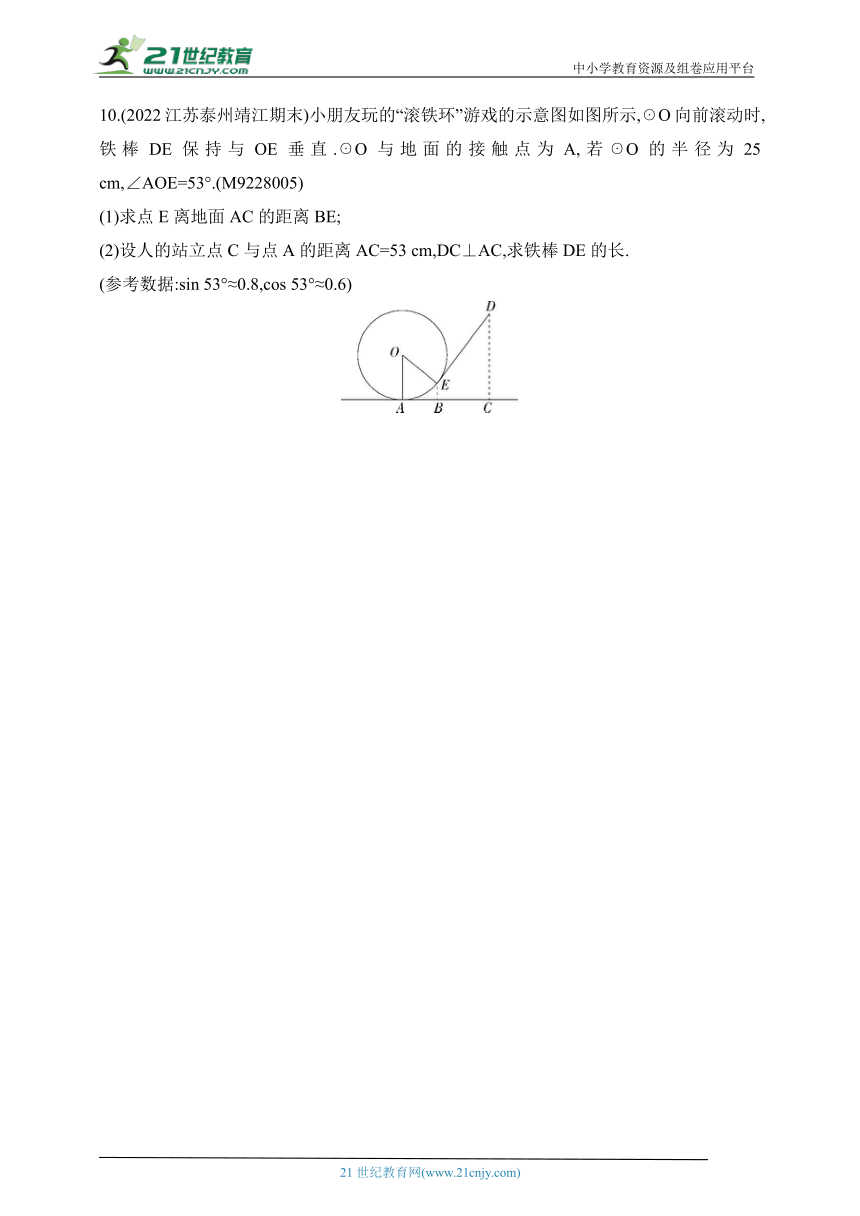
10.(2022江苏泰州靖江期末)小朋友玩的“滚铁环”游戏的示意图如图所示,☉O向前滚动时,铁棒DE保持与OE垂直.☉O与地面的接触点为A,若☉O的半径为25 cm,∠AOE=53°.(M9228005)
(1)求点E离地面AC的距离BE;
(2)设人的站立点C与点A的距离AC=53 cm,DC⊥AC,求铁棒DE的长.
(参考数据:sin 53°≈0.8,cos 53°≈0.6)
答案全解全析
1.C ∵可疑船只C在港口A北偏东30°方向上,驱逐舰B在港口A北偏东60°方向上,∴∠CAB=60°-30°=30°,∵驱逐舰B在可疑船只C的南偏东30°方向上,∴∠ACB=30°+30°=60°,∴∠ABC=180°-30°-60°=90°,∵sin∠ACB=,AB=10 km,∴AC=(km).故选C.
2.6.4
解析 在Rt△ABC中,∠CBA=32.7°,BC=10 cm,∴AC=BC·tan 32.7°≈10×0.64=6.4(cm),∴肿瘤在皮下的深度AC约为6.4 cm.
3.解析 由题知∠D=50°,∠ABD=140°,BD=520 m,BC=80 m,∴∠DBE=40°,
∴∠DEB=180°-∠DBE-∠D=180°-40°-50°=90°,
∴△DEB是直角三角形,
∴sin D=,∴0.77≈,∴BE≈400.4 m,
∴CE=BE-BC=400.4-80=320.4(m),
即公路CE段的长度约为320.4 m.
4.275米
解析 由已知得∠ECA=29.5°,∠FCB=45°,CD=100米,EF∥AB,CD⊥AB,∴∠A=∠ECA=29.5°,∠B=∠FCB=45°,∴△BCD是等腰直角三角形,∴BD=CD=100米.在Rt△ACD中,∠CDA=90°,tan A=≈175.4(米),∴AB=AD+BD=175.4+100≈275(米),即A、B之间的距离约为275米.
5.50
解析 设AB与圆C的切点为D,连接CD,则CD⊥AB.由题意,知CD=r.在Rt△ACD中,∠ACD=α,tan α=1.627,∵tan α=,∴AD=rtan α=1.627r,在Rt△BCD中,∠BCD=β,tan β=1.373,∵tan β=,∴BD=rtan β=1.373r,∵AD+BD=AB,∴1.627r+1.373r=150,∴r=50(km).
6.解析 如图所示,
过P作 PH⊥AB于H,过C作CQ⊥PH于Q,又 CB⊥AB,
则四边形 CQHB是矩形,
∴QH=BC,BH=CQ.
由题意可得AP=80,∠PAH=∠1=60°,∠PCQ=∠2=30°,AB=70,
∴PH=AP·sin 60°=80×,AH=AP·cos 60°=40,
∴CQ=BH=AB-AH=70-40=30,
∴PQ=CQ·tan 30°=10,
∴BC=QH=PH-PQ=40,
∴大楼的高度BC为30 米.
7.(23+0.5)
解析 设AG=x米,在Rt△AFG中,∠AFG=60°,tan∠AFG=x米,在Rt△AEG中,∠AEG=30°,tan∠AEG=x米,∴x=46,解得x=23米,则AB=(23+0.5)米,即明珠塔的高AB为(23+0.5)米.
8.335
解析 由题意,得BO⊥OD,在Rt△AOD中,AD=4 000米,∠ADO=30°,∴AO=AD=2 000(米),OD=OA=2 000(米),∵CD=460米,∴OC=OD-CD=(2 000-460)米,在Rt△BOC中,∠BCO=45°,∴BO=OC·tan 45°=(2 000-460)米,∴AB=BO-AO=2 000-460-2 000≈1 004(米),∴火箭从A处上升到B处的平均速度=≈335(米/秒).
9.(4+6)
解析 如图,过点D作DH⊥BE,垂足为H,过点D作DG⊥AB,垂足为G,则DH=GB,DG=BH,∵斜坡CF的坡比i=1∶3,∴.设DH=a米,则CH=3a米,在Rt△DHC中,DC=a(米),∵DC=2 米,∴,∴a=2,∴DH=GB=2米,CH=3a=6米,设BC=x米,则DG=BH=BC+CH=(x+6)米,在Rt△ABC中,∠ACB=45°,∴AB=BC·tan 45°=x米,∴AG=AB-BG=(x-2)米,在Rt△ADG中,∠ADG=30°,∴tan 30°=,解得x=4+6,经检验,x=4+6是原方程的解,∴AB=(4+6)米.
10.解析 如图,过E作与AC平行的直线,与OA、DC分别相交于H、N.
(1)在Rt△OHE中,∠OHE=90°,OE=25 cm,∠HOE=53°,∴HO=OE·cos 53°≈15 cm,
∴EB=HA=25-15=10(cm),
∴点E离地面AC的距离BE约为10 cm.
(2)∵∠EOH+∠OEH=∠OEH+∠DEN=90°,
∴∠DEN=∠EOH=53°,
∵EH=OE·sin∠HOE≈20 cm,∴EN=HN-HE=AC-HE=53-20=33(cm).在Rt△DEN中,∠DNE=90°,DE==55(cm),
∴铁棒DE的长约为55 cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版数学九年级下学期
专项素养综合全练(六)
解直角三角形实际应用的常见类型
类型一 解一个直角三角形
1.(2023山东泰安东平二模)
某驱逐舰在海上执行任务后刚返回到港口A,接到上级指令,发现在其北偏东30°方向上有一艘可疑船只C,与此同时在港口A北偏东60°方向上且距离10 km处有另一艘驱逐舰B也收到了相关指令,驱逐舰B恰好在可疑船只C的南偏东30°方向上,则可疑船只C与港口A之间的距离为( )
A. km B. km
C. km D.10 km
2.【新素材】(2022广东深圳龙华二模)如图,一名患者体内某重要器官后面有一肿瘤在A处.在接受放射性治疗时,为了最大限度地保证疗效,并且防止伤害器官,射线必须从侧面照射肿瘤.已知射线从肿瘤右侧10 cm的B处进入身体,且射线与皮肤所成的夹角∠CBA=32.7°,则肿瘤在皮下的深度AC约为 cm.(参考数据:sin 32.7°≈0.54,cos 32.7°≈0.84,tan 32.7°≈0.64)
3.(2022湖北襄阳襄城模拟)如图,沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工.从AC上的一点B取∠ABD=140°,沿BD方向前进,取∠BDE=50°,测得BD=520 m,BC=80 m,使A、C、E三点在同一直线上,求公路CE段的长度.(结果保留小数点后一位)(参考数据:sin 50°≈0.77,cos 50°≈0.64,tan 50°≈1.19)
类型二 “背靠背”型
4.(2023山西太原杏花岭模拟)如图,从热气球C上测得两建筑物底部A、B的俯角分别为29.5°和45°,如果这时热气球的高度CD为100米,且点A、D、B在同一直线上,则A、B之间的距离为 .(结果精确到1米)(参考数据:sin 29.5°≈0.49,cos 29.5°≈0.87,tan 29.5°≈0.57)
5.(2023湖北武汉武昌一模)A,B两市相距150 km,分别从A,B处测得某风景区中心C处的方向角如图所示,tan α=1.627,tan β=1.373.已知风景区是以C为圆心,r为半径的圆形区域.为了开发旅游,有关部门设计、修建连接A,B两市的高速公路,则r= km时,高速公路正好经过风景区的边界.
6.(2023山东菏泽中考)无人机在实际生活中的应用越来越广泛.如图所示,某人利用无人机测量大楼的高度BC,无人机在空中点P处,测得点P距地面上的点A 80米,点A处的俯角为60°,楼顶点C处的俯角为30°,已知点A与大楼的距离AB为70米(点A,B,C,P在同一平面内),求大楼的高度BC(结果保留根号).
类型三 “母子”型
7.(2023广西贵港平南模拟)明珠塔是一栋古代工艺与现代工艺完美融合的中式建筑.数学活动课上,老师带领兴趣小组去测量明珠塔的高度.如图,在C处用高0.5米的仪器CE测得塔顶A的仰角为30°,向塔的方向前进46米到达D处,此时测得塔顶A的仰角为60°,则明珠塔的高AB为 米(结果保留根号).
类型四 “拥抱”型
8.【国防科技】(2023湖北武汉江汉模拟)
如图,一枚火箭从地面O处成功发射,当火箭到达点A处时,地面D处的雷达站测得AD=4 000米,仰角为30°,3秒后,火箭竖直上升到达点B处,此时地面C处的雷达站测得B处的仰角为45°.已知点O,C,D在同一直线上,C,D两处相距460米,则火箭从A处上升到B处的平均速度为 米/秒.(结果精确到1米/秒;参考数据:≈1.732,≈1.414)
9.(2022山东烟台牟平一模)如图,一名高山滑雪运动员沿着斜坡FC滑行,他在点D处测得大树顶端A的仰角为30°,从D点再滑行2 米到达坡底的C点,在点C处测得大树顶端A的仰角为45°,若斜坡CF的坡比i=1∶3(点E,C,B在同一水平线上),则大树的高度AB为
米(结果保留根号).
10.(2022江苏泰州靖江期末)小朋友玩的“滚铁环”游戏的示意图如图所示,☉O向前滚动时,铁棒DE保持与OE垂直.☉O与地面的接触点为A,若☉O的半径为25 cm,∠AOE=53°.(M9228005)
(1)求点E离地面AC的距离BE;
(2)设人的站立点C与点A的距离AC=53 cm,DC⊥AC,求铁棒DE的长.
(参考数据:sin 53°≈0.8,cos 53°≈0.6)
答案全解全析
1.C ∵可疑船只C在港口A北偏东30°方向上,驱逐舰B在港口A北偏东60°方向上,∴∠CAB=60°-30°=30°,∵驱逐舰B在可疑船只C的南偏东30°方向上,∴∠ACB=30°+30°=60°,∴∠ABC=180°-30°-60°=90°,∵sin∠ACB=,AB=10 km,∴AC=(km).故选C.
2.6.4
解析 在Rt△ABC中,∠CBA=32.7°,BC=10 cm,∴AC=BC·tan 32.7°≈10×0.64=6.4(cm),∴肿瘤在皮下的深度AC约为6.4 cm.
3.解析 由题知∠D=50°,∠ABD=140°,BD=520 m,BC=80 m,∴∠DBE=40°,
∴∠DEB=180°-∠DBE-∠D=180°-40°-50°=90°,
∴△DEB是直角三角形,
∴sin D=,∴0.77≈,∴BE≈400.4 m,
∴CE=BE-BC=400.4-80=320.4(m),
即公路CE段的长度约为320.4 m.
4.275米
解析 由已知得∠ECA=29.5°,∠FCB=45°,CD=100米,EF∥AB,CD⊥AB,∴∠A=∠ECA=29.5°,∠B=∠FCB=45°,∴△BCD是等腰直角三角形,∴BD=CD=100米.在Rt△ACD中,∠CDA=90°,tan A=≈175.4(米),∴AB=AD+BD=175.4+100≈275(米),即A、B之间的距离约为275米.
5.50
解析 设AB与圆C的切点为D,连接CD,则CD⊥AB.由题意,知CD=r.在Rt△ACD中,∠ACD=α,tan α=1.627,∵tan α=,∴AD=rtan α=1.627r,在Rt△BCD中,∠BCD=β,tan β=1.373,∵tan β=,∴BD=rtan β=1.373r,∵AD+BD=AB,∴1.627r+1.373r=150,∴r=50(km).
6.解析 如图所示,
过P作 PH⊥AB于H,过C作CQ⊥PH于Q,又 CB⊥AB,
则四边形 CQHB是矩形,
∴QH=BC,BH=CQ.
由题意可得AP=80,∠PAH=∠1=60°,∠PCQ=∠2=30°,AB=70,
∴PH=AP·sin 60°=80×,AH=AP·cos 60°=40,
∴CQ=BH=AB-AH=70-40=30,
∴PQ=CQ·tan 30°=10,
∴BC=QH=PH-PQ=40,
∴大楼的高度BC为30 米.
7.(23+0.5)
解析 设AG=x米,在Rt△AFG中,∠AFG=60°,tan∠AFG=x米,在Rt△AEG中,∠AEG=30°,tan∠AEG=x米,∴x=46,解得x=23米,则AB=(23+0.5)米,即明珠塔的高AB为(23+0.5)米.
8.335
解析 由题意,得BO⊥OD,在Rt△AOD中,AD=4 000米,∠ADO=30°,∴AO=AD=2 000(米),OD=OA=2 000(米),∵CD=460米,∴OC=OD-CD=(2 000-460)米,在Rt△BOC中,∠BCO=45°,∴BO=OC·tan 45°=(2 000-460)米,∴AB=BO-AO=2 000-460-2 000≈1 004(米),∴火箭从A处上升到B处的平均速度=≈335(米/秒).
9.(4+6)
解析 如图,过点D作DH⊥BE,垂足为H,过点D作DG⊥AB,垂足为G,则DH=GB,DG=BH,∵斜坡CF的坡比i=1∶3,∴.设DH=a米,则CH=3a米,在Rt△DHC中,DC=a(米),∵DC=2 米,∴,∴a=2,∴DH=GB=2米,CH=3a=6米,设BC=x米,则DG=BH=BC+CH=(x+6)米,在Rt△ABC中,∠ACB=45°,∴AB=BC·tan 45°=x米,∴AG=AB-BG=(x-2)米,在Rt△ADG中,∠ADG=30°,∴tan 30°=,解得x=4+6,经检验,x=4+6是原方程的解,∴AB=(4+6)米.
10.解析 如图,过E作与AC平行的直线,与OA、DC分别相交于H、N.
(1)在Rt△OHE中,∠OHE=90°,OE=25 cm,∠HOE=53°,∴HO=OE·cos 53°≈15 cm,
∴EB=HA=25-15=10(cm),
∴点E离地面AC的距离BE约为10 cm.
(2)∵∠EOH+∠OEH=∠OEH+∠DEN=90°,
∴∠DEN=∠EOH=53°,
∵EH=OE·sin∠HOE≈20 cm,∴EN=HN-HE=AC-HE=53-20=33(cm).在Rt△DEN中,∠DNE=90°,DE==55(cm),
∴铁棒DE的长约为55 cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
