2024人教版数学九年级下学期课时练--专项素养综合全练(九)新定义型试题(含解析)
文档属性
| 名称 | 2024人教版数学九年级下学期课时练--专项素养综合全练(九)新定义型试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 473.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 09:39:26 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024人教版数学九年级下学期
专项素养综合全练(九)
新定义型试题
类型一 定义新运算型
1.【新独家原创】如果规定符号“△”的意义是a△b=,则(-4tan 45°)△(8sin 60°cos 30°)的值是( )
A.-12 B.12 C.2.4 D.-6
2.如果规定符号“ ”的意义为a b=,当a=tan 60°,b=2sin 30°时,a b的值是( )
A.-2+
C.1-
3.定义新运算:对于任意实数m、n都有m@n=m2+.已知,在△ABC中,锐角∠A、∠B满足-2sin A)=0,则△ABC是 三角形.
类型二 定义新概念型
4.【射影模型】设a>0,b>0,称为a,b的“调和平均数”,如图,C为线段AB上的点,且AC=a,BC=b,O是AB的中点,以AB为直径作半圆,过点C作AB的垂线交半圆于D,连接OD,AD,BD,过点C作OD的垂线,垂足为E,若图中的线段OD的长度是a,b的算术平均数,则长度是a,b的“调和平均数”的线段是( )
A.OC B.CE C.DE D.OE
5.【分类讨论思想】(2023江苏盐城东台月考)定义:在直角三角形ABC中,∠C=90°,把∠A的邻边与对边的比叫做∠A的余切,记作cot A.等腰三角形中有两条边长为4和6,则底角的余切值为 .
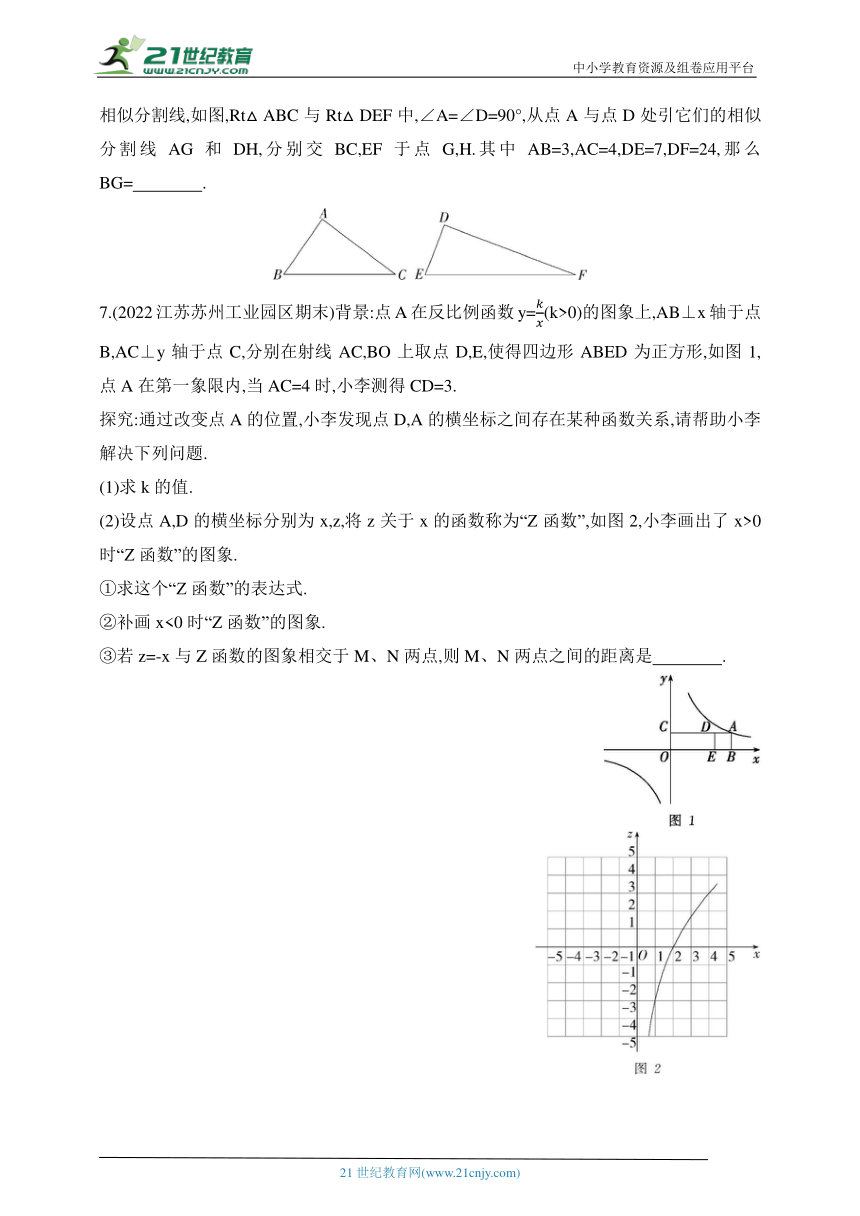
6.(2021上海静安期中)在冲刺中考的日子里,小明更加努力学习,尤其善于总结研究,他发现:即使不相似的两个直角三角形,也可以用直线把它们分割成两对分别相似的三角形.于是他提出以下新定义问题:在两个不相似的直角三角形中,如果第一个直角三角形分割出来的一个小三角形与第二个直角三角形分割出来的一个小三角形相似,且分割出来的另外两个小三角形也相似,那么把这样的分割三角形的两条直线称为这两个直角三角形的相似分割线,如图,Rt△ABC与Rt△DEF中,∠A=∠D=90°,从点A与点D处引它们的相似分割线AG和DH,分别交BC,EF于点G,H.其中AB=3,AC=4,DE=7,DF=24,那么BG= .
7.(2022江苏苏州工业园区期末)背景:点A在反比例函数y=(k>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,分别在射线AC,BO上取点D,E,使得四边形ABED为正方形,如图1,点A在第一象限内,当AC=4时,小李测得CD=3.
探究:通过改变点A的位置,小李发现点D,A的横坐标之间存在某种函数关系,请帮助小李解决下列问题.
(1)求k的值.
(2)设点A,D的横坐标分别为x,z,将z关于x的函数称为“Z函数”,如图2,小李画出了x>0时“Z函数”的图象.
①求这个“Z函数”的表达式.
②补画x<0时“Z函数”的图象.
③若z=-x与Z函数的图象相交于M、N两点,则M、N两点之间的距离是 .
类型三 定义新方法型
8.【新考向·阅读理解试题】阅读材料:
关于三角函数有如下的公式:
sin(α-β)=sin αcos β-cos αsin β;
tan(α-β)=.
利用这些公式可以将一些非特殊角的三角函数转化为特殊角的三角函数来求值.
例:tan 15°=tan(45°-30°)=.
根据以上阅读材料,请选择适当的公式解答下面问题:
(1)计算:sin 15°;
(2)乌蒙铁塔是六盘水市标志性建筑物之一(如图①),小华想用所学知识来测量该铁塔的高度,如图②,小华站在离塔底A 8米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.62米,请帮助小华求出乌蒙铁塔的高度.(精确到0.1米,参考数据:≈1.732,≈1.414)
答案全解全析
1.A ∵tan 45°=1,sin 60°=cos 30°=,a△b=,∴(-4tan 45°)△(8sin 60°cos 30°)=(-4×1)△(8×)=(-4)△6==-12.故选A.
2.B ∵tan 60°=,2sin 30°=2×=1,
∴a b= 1=.故选B.
3.直角
解析 由题意,得=0,
∴tan B--2sin A=0,∴tan B=,sin A=,∴∠B=30°,∠A=60°,∴∠C=180°-(∠A+∠B)=90°,∴△ABC是直角三角形.
4.C ∵AB是半圆的直径,∴∠ADB=90°,∵DC⊥AB,∴∠BCD=90°,易得△ACD∽△DCB,∴,即CD2=AC·BC=ab.∵线段OD的长度是a,b的算术平均数,∴OD=.由DC⊥OC,CE⊥OD易得△OCD∽△CED,∴,即CD2=DE·OD,∴DE=,∴线段DE的长度是a,b的“调和平均数”.故选C.
5.
解析 如图1,其中AB=AC=6,BC=4,过A作AD⊥BC于D,则BD=CD=2,∴AD=,∴cot B=;如图2,其中AB=AC=4,BC=6,过A作AD⊥BC于D,则BD=CD=3,∴AD=,∴cot B=.
6.
解析 ∵AB=3,AC=4,DE=7,DF=24,∠BAC=∠EDF=90°,
∴BC==25.
有两种情形:(1)如图①,当△ABG∽△FDH时,设BG=x,则CG=5-x.∵△ABG∽△FDH,∴,即,∴DH=8x,∵△ABG∽△FDH,∴∠AGB=∠DHF,∠BAG=∠F,∴∠AGC=∠DHE,∵∠BAG+∠CAG=90°,∠F+∠E=90°,∴∠CAG=∠E,∴△CAG∽△DEH,∴,解得x=,即BG=.
(2)如图②,当△ABG∽△EDH时,设BG=y,则CG=5-y.∵△ABG∽△EDH,∴,即y,∵△ABG∽△EDH,∴∠AGB=∠EHD,∠BAG=∠DEH,∴∠AGC=∠DHF,∵∠BAG+∠CAG=90°,∠F+∠E=90°,∴∠CAG=∠F,∴△AGC∽△FHD,∴,解得y=,即BG=.
综上所述,BG=.
7.解析 (1)当AC=4,CD=3时,AD=1,
∵四边形ABED是正方形,
∴AD=AB=1,∴A(4,1),
∵点A在反比例函数y=(k>0)的图象上,
∴k=4×1=4.
(2)①由题意知,A(x,x-z),∴x(x-z)=4,
∴z=x-.
②如图.
③4.
详解:当-x=x-时,x=±,不妨令M(-),则MN==4.
8.解析 (1)sin 15°=sin(45°-30°)
=sin 45°cos 30°-cos 45°sin 30°
=.
(2)在Rt△BDE中,
∵∠BED=90°,∠BDE=75°,∴∠DBE=15°.
又DE=AC=8米,
∴BE=)米.
∴AB=AE+BE=1.62+16+8≈31.5(米).
答:乌蒙铁塔的高度约为31.5米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版数学九年级下学期
专项素养综合全练(九)
新定义型试题
类型一 定义新运算型
1.【新独家原创】如果规定符号“△”的意义是a△b=,则(-4tan 45°)△(8sin 60°cos 30°)的值是( )
A.-12 B.12 C.2.4 D.-6
2.如果规定符号“ ”的意义为a b=,当a=tan 60°,b=2sin 30°时,a b的值是( )
A.-2+
C.1-
3.定义新运算:对于任意实数m、n都有m@n=m2+.已知,在△ABC中,锐角∠A、∠B满足-2sin A)=0,则△ABC是 三角形.
类型二 定义新概念型
4.【射影模型】设a>0,b>0,称为a,b的“调和平均数”,如图,C为线段AB上的点,且AC=a,BC=b,O是AB的中点,以AB为直径作半圆,过点C作AB的垂线交半圆于D,连接OD,AD,BD,过点C作OD的垂线,垂足为E,若图中的线段OD的长度是a,b的算术平均数,则长度是a,b的“调和平均数”的线段是( )
A.OC B.CE C.DE D.OE
5.【分类讨论思想】(2023江苏盐城东台月考)定义:在直角三角形ABC中,∠C=90°,把∠A的邻边与对边的比叫做∠A的余切,记作cot A.等腰三角形中有两条边长为4和6,则底角的余切值为 .
6.(2021上海静安期中)在冲刺中考的日子里,小明更加努力学习,尤其善于总结研究,他发现:即使不相似的两个直角三角形,也可以用直线把它们分割成两对分别相似的三角形.于是他提出以下新定义问题:在两个不相似的直角三角形中,如果第一个直角三角形分割出来的一个小三角形与第二个直角三角形分割出来的一个小三角形相似,且分割出来的另外两个小三角形也相似,那么把这样的分割三角形的两条直线称为这两个直角三角形的相似分割线,如图,Rt△ABC与Rt△DEF中,∠A=∠D=90°,从点A与点D处引它们的相似分割线AG和DH,分别交BC,EF于点G,H.其中AB=3,AC=4,DE=7,DF=24,那么BG= .
7.(2022江苏苏州工业园区期末)背景:点A在反比例函数y=(k>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,分别在射线AC,BO上取点D,E,使得四边形ABED为正方形,如图1,点A在第一象限内,当AC=4时,小李测得CD=3.
探究:通过改变点A的位置,小李发现点D,A的横坐标之间存在某种函数关系,请帮助小李解决下列问题.
(1)求k的值.
(2)设点A,D的横坐标分别为x,z,将z关于x的函数称为“Z函数”,如图2,小李画出了x>0时“Z函数”的图象.
①求这个“Z函数”的表达式.
②补画x<0时“Z函数”的图象.
③若z=-x与Z函数的图象相交于M、N两点,则M、N两点之间的距离是 .
类型三 定义新方法型
8.【新考向·阅读理解试题】阅读材料:
关于三角函数有如下的公式:
sin(α-β)=sin αcos β-cos αsin β;
tan(α-β)=.
利用这些公式可以将一些非特殊角的三角函数转化为特殊角的三角函数来求值.
例:tan 15°=tan(45°-30°)=.
根据以上阅读材料,请选择适当的公式解答下面问题:
(1)计算:sin 15°;
(2)乌蒙铁塔是六盘水市标志性建筑物之一(如图①),小华想用所学知识来测量该铁塔的高度,如图②,小华站在离塔底A 8米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.62米,请帮助小华求出乌蒙铁塔的高度.(精确到0.1米,参考数据:≈1.732,≈1.414)
答案全解全析
1.A ∵tan 45°=1,sin 60°=cos 30°=,a△b=,∴(-4tan 45°)△(8sin 60°cos 30°)=(-4×1)△(8×)=(-4)△6==-12.故选A.
2.B ∵tan 60°=,2sin 30°=2×=1,
∴a b= 1=.故选B.
3.直角
解析 由题意,得=0,
∴tan B--2sin A=0,∴tan B=,sin A=,∴∠B=30°,∠A=60°,∴∠C=180°-(∠A+∠B)=90°,∴△ABC是直角三角形.
4.C ∵AB是半圆的直径,∴∠ADB=90°,∵DC⊥AB,∴∠BCD=90°,易得△ACD∽△DCB,∴,即CD2=AC·BC=ab.∵线段OD的长度是a,b的算术平均数,∴OD=.由DC⊥OC,CE⊥OD易得△OCD∽△CED,∴,即CD2=DE·OD,∴DE=,∴线段DE的长度是a,b的“调和平均数”.故选C.
5.
解析 如图1,其中AB=AC=6,BC=4,过A作AD⊥BC于D,则BD=CD=2,∴AD=,∴cot B=;如图2,其中AB=AC=4,BC=6,过A作AD⊥BC于D,则BD=CD=3,∴AD=,∴cot B=.
6.
解析 ∵AB=3,AC=4,DE=7,DF=24,∠BAC=∠EDF=90°,
∴BC==25.
有两种情形:(1)如图①,当△ABG∽△FDH时,设BG=x,则CG=5-x.∵△ABG∽△FDH,∴,即,∴DH=8x,∵△ABG∽△FDH,∴∠AGB=∠DHF,∠BAG=∠F,∴∠AGC=∠DHE,∵∠BAG+∠CAG=90°,∠F+∠E=90°,∴∠CAG=∠E,∴△CAG∽△DEH,∴,解得x=,即BG=.
(2)如图②,当△ABG∽△EDH时,设BG=y,则CG=5-y.∵△ABG∽△EDH,∴,即y,∵△ABG∽△EDH,∴∠AGB=∠EHD,∠BAG=∠DEH,∴∠AGC=∠DHF,∵∠BAG+∠CAG=90°,∠F+∠E=90°,∴∠CAG=∠F,∴△AGC∽△FHD,∴,解得y=,即BG=.
综上所述,BG=.
7.解析 (1)当AC=4,CD=3时,AD=1,
∵四边形ABED是正方形,
∴AD=AB=1,∴A(4,1),
∵点A在反比例函数y=(k>0)的图象上,
∴k=4×1=4.
(2)①由题意知,A(x,x-z),∴x(x-z)=4,
∴z=x-.
②如图.
③4.
详解:当-x=x-时,x=±,不妨令M(-),则MN==4.
8.解析 (1)sin 15°=sin(45°-30°)
=sin 45°cos 30°-cos 45°sin 30°
=.
(2)在Rt△BDE中,
∵∠BED=90°,∠BDE=75°,∴∠DBE=15°.
又DE=AC=8米,
∴BE=)米.
∴AB=AE+BE=1.62+16+8≈31.5(米).
答:乌蒙铁塔的高度约为31.5米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
