2024人教版数学九年级下学期课时练--专项素养综合全练(七)相似、解直角三角形中的难点模型(含解析)
文档属性
| 名称 | 2024人教版数学九年级下学期课时练--专项素养综合全练(七)相似、解直角三角形中的难点模型(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 519.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 09:40:47 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024人教版数学九年级下学期
专项素养综合全练(七)
相似、解直角三角形中的难点模型
类型一 射影模型
1.(2022福建漳州期末)如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为D,AD=3,CD=4,则BD的长为( )
A. D.2
2.(2023安徽合肥包河期中)如图,在△ABC中,CD⊥AB于点D,有下列条件:①∠A=∠BCD;②∠A+∠BCD=∠ADC;③;④BC2=BD·BA.其中能判定△ABC是直角三角形的有( )
A.0个 B.1个 C.2个 D.3个
3.(2022四川广元中考改编)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的☉O交AB于点D.若AD=4,BD=9,则☉O的半径为 .
类型二 胡不归模型
专题解读 如图,动点P在定直线上,求形如“PA+kPB”(04.(2023安徽合肥一模)如图,△ABC为等边三角形,BD平分∠ABC,AB=2,点E为BD上一动点,连接AE,则AE+BE的最小值为( )
A.1 B. D.2
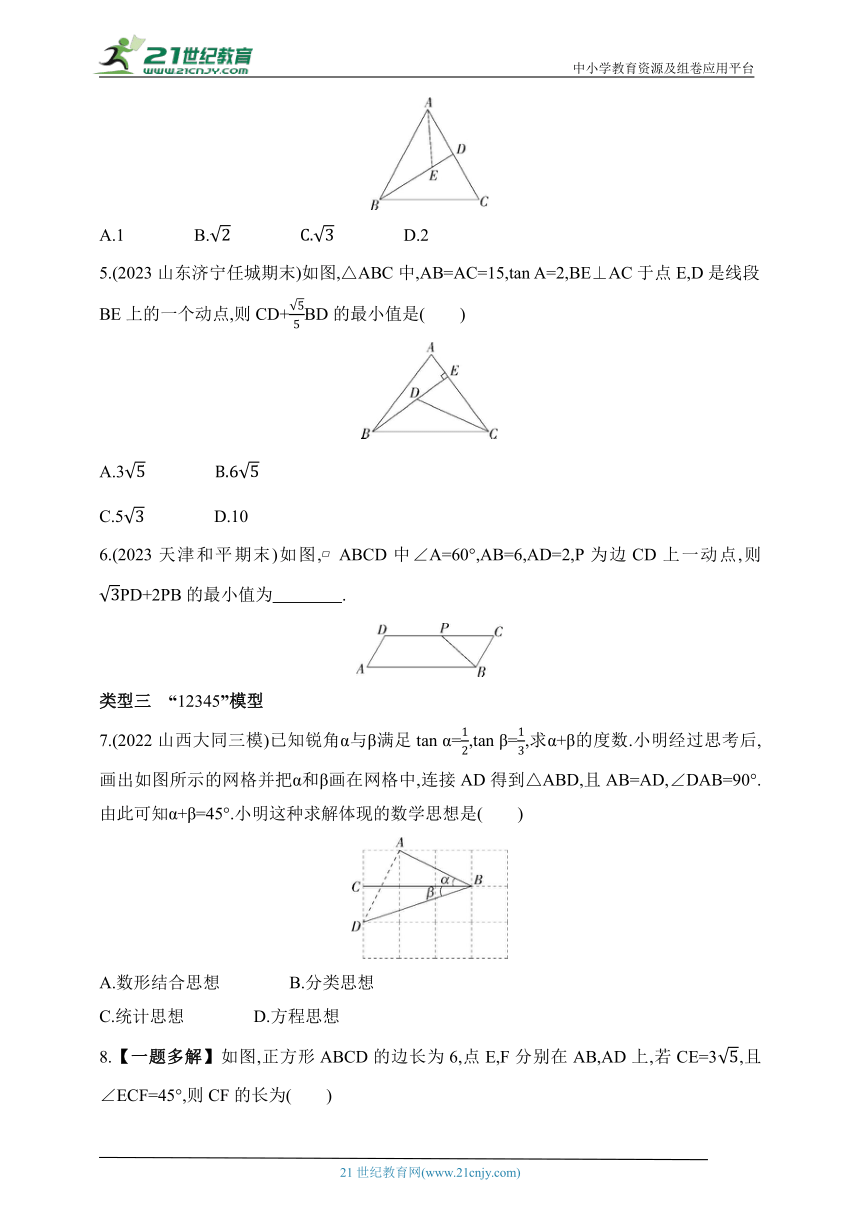
5.(2023山东济宁任城期末)如图,△ABC中,AB=AC=15,tan A=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是( )
A.3
C.5 D.10
6.(2023天津和平期末)如图, ABCD中∠A=60°,AB=6,AD=2,P为边CD上一动点,则PD+2PB的最小值为 .
类型三 “12345”模型
7.(2022山西大同三模)已知锐角α与β满足tan α=,tan β=,求α+β的度数.小明经过思考后,画出如图所示的网格并把α和β画在网格中,连接AD得到△ABD,且AB=AD,∠DAB=90°.由此可知α+β=45°.小明这种求解体现的数学思想是( )
A.数形结合思想 B.分类思想
C.统计思想 D.方程思想
8.【一题多解】如图,正方形ABCD的边长为6,点E,F分别在AB,AD上,若CE=3,且∠ECF=45°,则CF的长为( )
A.2
C.
9.【新考向·阅读理解试题】(2023四川凉山州中考)阅读材料:如图①,四边形ABCD是矩形,△AEF是等腰直角三角形,记∠BAE为α、∠FAD为β,若tan α=,则tan β=.
证明:设BE=k,∵tan α=,∴AB=2k,易证△AEB≌△EFC(AAS),∴EC=2k,CF=k,∴FD=k,AD=3k,∴tan β=,∴当α+β=45°时,若tan α=,则tan β=.
同理,当α+β=45°时,若tan α=,则tan β=.
根据上述材料,完成下列问题:
如图②,直线y=3x-9与反比例函数y=(x>0)的图象交于点A,与x轴交于点B.直线AB绕点A顺时针旋转45°后与y轴交于点E,过点A作AM⊥x轴于点M,过点A作AN⊥y轴于点N,已知OA=5.
(1)求反比例函数的解析式;
(2)直接写出tan∠BAM、tan∠NAE的值;
(3)求直线AE的解析式.
类型四 阿氏圆模型
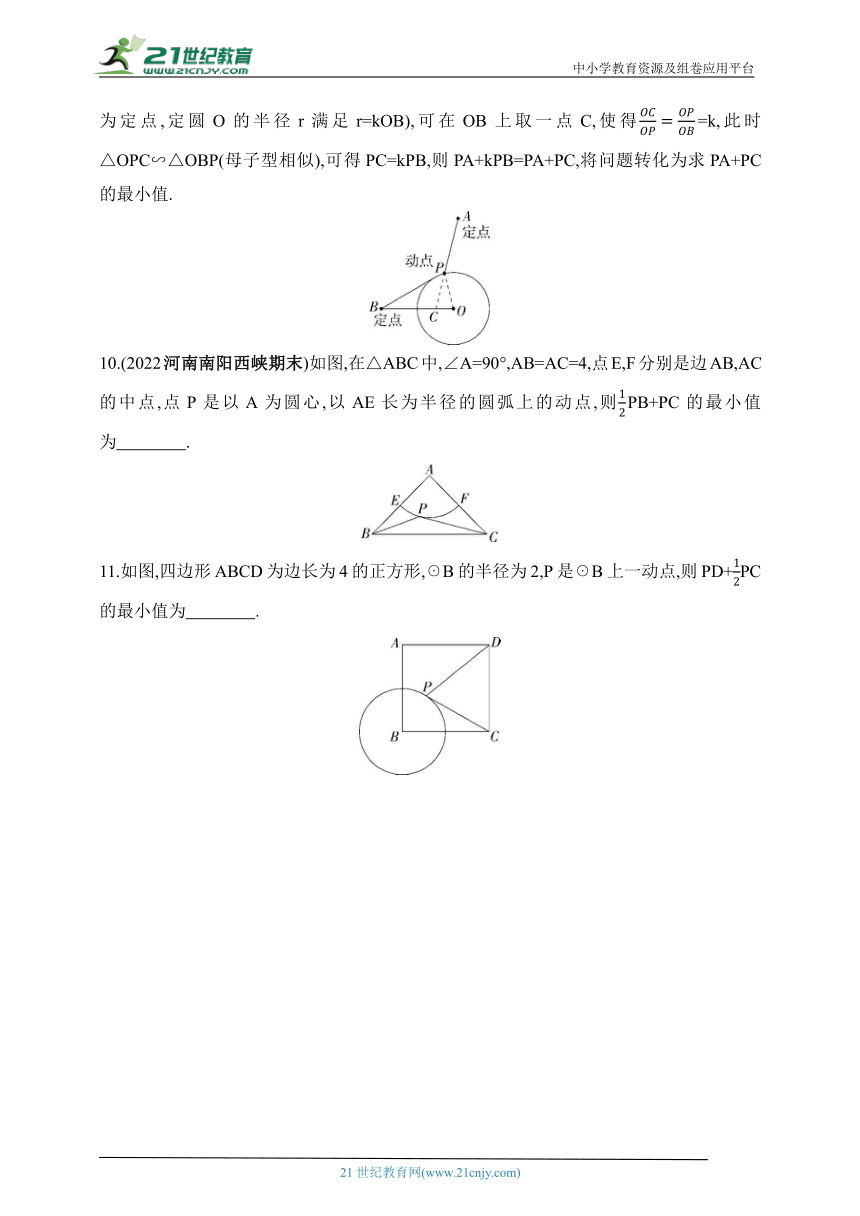
专题解读 如图,动点P在定圆上,求形如“PA+kPB” (010.(2022河南南阳西峡期末)如图,在△ABC中,∠A=90°,AB=AC=4,点E,F分别是边AB,AC的中点,点P是以A为圆心,以AE长为半径的圆弧上的动点,则PB+PC的最小值为 .
11.如图,四边形ABCD为边长为4的正方形,☉B的半径为2,P是☉B上一动点,则PD+PC的最小值为 .
答案全解全析
A ∵∠BAC=90°,∴∠B+∠C=90°.
∵AD⊥BC,∴∠ADB=∠ADC=90°,
∴∠DAC+∠C=90°,∴∠B=∠DAC,
∴△BDA∽△ADC,∴.故选A.
模型归纳 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,那么有:①CD2=AD·BD;②AC2=AB·AD;③BC2=AB·BD.
2.D ①∵∠A=∠BCD,∠A+∠ACD=90°,∴∠BCD+∠ACD=90°,即∠ACB=90°,故①符合题意;②条件不足,无法判定△ABC是直角三角形,故②不符合题意;③∵BD∶CD=BC∶AC,∠ADC=∠CDB=90°,∴Rt△ADC∽Rt△CDB,∴∠ACD=∠B,∵∠B+∠BCD=90°,∴∠ACD+∠BCD=90°,∴∠ACB=90°,故③符合题意;④∵BC2=BD·BA,∴,∵∠B=∠B,∴△ABC∽△CBD,∴∠ACB=90°,故④符合题意.故选D.
3.
解析 如图,连接CD,∵AC是☉O的直径,∴∠ADC=90°,∵AD=4,BD=9,∴AB=AD+BD=4+9=13,∵∠ACB=∠ADC=90°,∠A=∠A,∴△ACB∽△ADC,∴,∴AC2=AD·AB=4×13=52,∴AC=2,∴☉O的半径为.
4.C 如图,过E作EM⊥BC于M,过A作AH⊥BC于H,交BD于E'.∵△ABC为等边三角形,BD平分∠ABC,∴∠EBM=30°,∴EM=BE=AE+EM,当AE+BE最小时,AE+EM最小,此时E与E'重合,M与H重合,则AE+BE的最小值为AH的长度,在Rt△ABH中,AH=AB·sin∠ABH=2×sin 60°=BE的最小值为.故选C.
5.B 如图,作DH⊥AB于H,CM⊥AB于M.∵BE⊥AC,∴∠AEB=90°,∵tan A==2,∴设AE=a,BE=2a,则有152=a2+4a2,∴a2=45,∴a=3(舍负),∴BE=2a=6,∵AB=AC,BE⊥AC,CM⊥AB,∴CM=BE=6,∵∠DBH=∠ABE,∠BHD=∠BEA,∴△BHD∽△BEA,∴BD=CD+DH,∵CD+DH≥CM,∴当点H与M重合时,CD+DH的值最小,∴CD+BD的最小值为线段CM的长,∴CD+BD的最小值为6.故选B.
6.6
解析 如图,过点P作PH⊥AD,交AD的延长线于H,过点B作BN⊥AH于N,∵四边形ABCD是平行四边形,∴AB∥CD,∴∠A=∠CDH=60°.∵HP⊥AD,∴∠DPH=30°,∴DH==2(HP+PB),∴当点H,点P,点B共线时,HP+PB有最小值,即PD+2PB有最小值,且最小值为2BN的值.∵BN⊥AH,∠A=60°,∴∠ABN=30°,∴AN=,则PD+2PB的最小值为2×3.
7.A 本题结合正切的定义,利用几何网格图进行分析,属于数形结合思想.故选A.
模型归纳 α和β是两个锐角,α+β=45°、tan α=、tan β=中,知二可推一.
8.A 解法一(利用“半角”模型):如图,延长FD到G,使DG=BE,连接CG,EF.四边形ABCD为正方形,在△BCE与△DCG中,∴△BCE≌△DCG(SAS),∴CG=CE,∠DCG=∠BCE,∴∠GCF=∠GCD+∠DCF=∠BCE+∠DCF=45°,在△GCF与△ECF中,∴△GCF≌△ECF(SAS),∴GF=EF,∵CE=3=3,∴AE=3,设AF=x,则DF=6-x,GF=3+(6-x)=9-x,EF=,∵GF2=EF2,∴(9-x)2=9+x2,∴x=4,即AF=4,∴DF=2,∴CF=.故选A.
解法二(利用“12345”模型):∵CE=3=3,∴tan∠BCE=.∵∠ECF=45°,∠BCD=90°,∴∠BCE+∠DCF=45°,∴tan∠DCF=,∴DF=2.在Rt△DCF中,CF=.故选A.
9.解析 (1)设A(t,3t-9),则OM=t,AM=3t-9,
∵OA=5,∴t2+(3t-9)2=52,
解得t=4或t=1.4,
∴A(4,3)或A(1.4,-4.8)(不合题意,舍去),
把A(4,3)代入y=,得3=,∴m=12,
∴反比例函数的解析式为y=.
(2)在y=3x-9中,令y=0,得0=3x-9,
解得x=3,∴B(3,0),∴OB=3.
由(1)知A(4,3),∴OM=4,AM=3,
∴BM=OM-OB=4-3=1,
∴tan∠BAM=.
∵∠ANO=∠NOM=∠OMA=90°,∴∠MAN=90°,
∵∠BAE=45°,∴∠BAM+∠NAE=45°.
由当α+β=45°时,若tan α=,则tan β=可得
tan∠NAE=.
(3)由(2)知tan∠NAE=.
∵A(4,3),∴AN=4,ON=3,
∴,∴NE=2,
∴OE=ON-NE=3-2=1,∴E(0,1),
设直线AE的解析式为y=kx+b,
把A(4,3),E(0,1)代入,
得
∴直线AE的解析式为y=x+1.
10.
解析 如图,在AB上截取AQ=1,连接AP,PQ,CQ,∵点E,F分别是边AB,AC的中点,点P是以A为圆心,以AE长为半径的圆弧上的动点,∴,∵∠PAQ=∠BAP,∴△APQ∽△ABP,∴PQ=PB+PC=PQ+PC≥CQ,在Rt△ACQ中,AC=4,AQ=1,∴QC=PB+PC的最小值为.
11.5
解析 如图,连接PB,在BC上取一点E,使得BE=1.∵PB2=4,BE·BC=4,∴PB2=BE·BC,∴,∵∠PBE=∠CBP,∴△PBE∽△CBP,∴PC=PD+PE,∵PE+PD≥DE,在Rt△DCE中,DE=PC的最小值为5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版数学九年级下学期
专项素养综合全练(七)
相似、解直角三角形中的难点模型
类型一 射影模型
1.(2022福建漳州期末)如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为D,AD=3,CD=4,则BD的长为( )
A. D.2
2.(2023安徽合肥包河期中)如图,在△ABC中,CD⊥AB于点D,有下列条件:①∠A=∠BCD;②∠A+∠BCD=∠ADC;③;④BC2=BD·BA.其中能判定△ABC是直角三角形的有( )
A.0个 B.1个 C.2个 D.3个
3.(2022四川广元中考改编)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的☉O交AB于点D.若AD=4,BD=9,则☉O的半径为 .
类型二 胡不归模型
专题解读 如图,动点P在定直线上,求形如“PA+kPB”(0
A.1 B. D.2
5.(2023山东济宁任城期末)如图,△ABC中,AB=AC=15,tan A=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是( )
A.3
C.5 D.10
6.(2023天津和平期末)如图, ABCD中∠A=60°,AB=6,AD=2,P为边CD上一动点,则PD+2PB的最小值为 .
类型三 “12345”模型
7.(2022山西大同三模)已知锐角α与β满足tan α=,tan β=,求α+β的度数.小明经过思考后,画出如图所示的网格并把α和β画在网格中,连接AD得到△ABD,且AB=AD,∠DAB=90°.由此可知α+β=45°.小明这种求解体现的数学思想是( )
A.数形结合思想 B.分类思想
C.统计思想 D.方程思想
8.【一题多解】如图,正方形ABCD的边长为6,点E,F分别在AB,AD上,若CE=3,且∠ECF=45°,则CF的长为( )
A.2
C.
9.【新考向·阅读理解试题】(2023四川凉山州中考)阅读材料:如图①,四边形ABCD是矩形,△AEF是等腰直角三角形,记∠BAE为α、∠FAD为β,若tan α=,则tan β=.
证明:设BE=k,∵tan α=,∴AB=2k,易证△AEB≌△EFC(AAS),∴EC=2k,CF=k,∴FD=k,AD=3k,∴tan β=,∴当α+β=45°时,若tan α=,则tan β=.
同理,当α+β=45°时,若tan α=,则tan β=.
根据上述材料,完成下列问题:
如图②,直线y=3x-9与反比例函数y=(x>0)的图象交于点A,与x轴交于点B.直线AB绕点A顺时针旋转45°后与y轴交于点E,过点A作AM⊥x轴于点M,过点A作AN⊥y轴于点N,已知OA=5.
(1)求反比例函数的解析式;
(2)直接写出tan∠BAM、tan∠NAE的值;
(3)求直线AE的解析式.
类型四 阿氏圆模型
专题解读 如图,动点P在定圆上,求形如“PA+kPB” (0
11.如图,四边形ABCD为边长为4的正方形,☉B的半径为2,P是☉B上一动点,则PD+PC的最小值为 .
答案全解全析
A ∵∠BAC=90°,∴∠B+∠C=90°.
∵AD⊥BC,∴∠ADB=∠ADC=90°,
∴∠DAC+∠C=90°,∴∠B=∠DAC,
∴△BDA∽△ADC,∴.故选A.
模型归纳 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,那么有:①CD2=AD·BD;②AC2=AB·AD;③BC2=AB·BD.
2.D ①∵∠A=∠BCD,∠A+∠ACD=90°,∴∠BCD+∠ACD=90°,即∠ACB=90°,故①符合题意;②条件不足,无法判定△ABC是直角三角形,故②不符合题意;③∵BD∶CD=BC∶AC,∠ADC=∠CDB=90°,∴Rt△ADC∽Rt△CDB,∴∠ACD=∠B,∵∠B+∠BCD=90°,∴∠ACD+∠BCD=90°,∴∠ACB=90°,故③符合题意;④∵BC2=BD·BA,∴,∵∠B=∠B,∴△ABC∽△CBD,∴∠ACB=90°,故④符合题意.故选D.
3.
解析 如图,连接CD,∵AC是☉O的直径,∴∠ADC=90°,∵AD=4,BD=9,∴AB=AD+BD=4+9=13,∵∠ACB=∠ADC=90°,∠A=∠A,∴△ACB∽△ADC,∴,∴AC2=AD·AB=4×13=52,∴AC=2,∴☉O的半径为.
4.C 如图,过E作EM⊥BC于M,过A作AH⊥BC于H,交BD于E'.∵△ABC为等边三角形,BD平分∠ABC,∴∠EBM=30°,∴EM=BE=AE+EM,当AE+BE最小时,AE+EM最小,此时E与E'重合,M与H重合,则AE+BE的最小值为AH的长度,在Rt△ABH中,AH=AB·sin∠ABH=2×sin 60°=BE的最小值为.故选C.
5.B 如图,作DH⊥AB于H,CM⊥AB于M.∵BE⊥AC,∴∠AEB=90°,∵tan A==2,∴设AE=a,BE=2a,则有152=a2+4a2,∴a2=45,∴a=3(舍负),∴BE=2a=6,∵AB=AC,BE⊥AC,CM⊥AB,∴CM=BE=6,∵∠DBH=∠ABE,∠BHD=∠BEA,∴△BHD∽△BEA,∴BD=CD+DH,∵CD+DH≥CM,∴当点H与M重合时,CD+DH的值最小,∴CD+BD的最小值为线段CM的长,∴CD+BD的最小值为6.故选B.
6.6
解析 如图,过点P作PH⊥AD,交AD的延长线于H,过点B作BN⊥AH于N,∵四边形ABCD是平行四边形,∴AB∥CD,∴∠A=∠CDH=60°.∵HP⊥AD,∴∠DPH=30°,∴DH==2(HP+PB),∴当点H,点P,点B共线时,HP+PB有最小值,即PD+2PB有最小值,且最小值为2BN的值.∵BN⊥AH,∠A=60°,∴∠ABN=30°,∴AN=,则PD+2PB的最小值为2×3.
7.A 本题结合正切的定义,利用几何网格图进行分析,属于数形结合思想.故选A.
模型归纳 α和β是两个锐角,α+β=45°、tan α=、tan β=中,知二可推一.
8.A 解法一(利用“半角”模型):如图,延长FD到G,使DG=BE,连接CG,EF.四边形ABCD为正方形,在△BCE与△DCG中,∴△BCE≌△DCG(SAS),∴CG=CE,∠DCG=∠BCE,∴∠GCF=∠GCD+∠DCF=∠BCE+∠DCF=45°,在△GCF与△ECF中,∴△GCF≌△ECF(SAS),∴GF=EF,∵CE=3=3,∴AE=3,设AF=x,则DF=6-x,GF=3+(6-x)=9-x,EF=,∵GF2=EF2,∴(9-x)2=9+x2,∴x=4,即AF=4,∴DF=2,∴CF=.故选A.
解法二(利用“12345”模型):∵CE=3=3,∴tan∠BCE=.∵∠ECF=45°,∠BCD=90°,∴∠BCE+∠DCF=45°,∴tan∠DCF=,∴DF=2.在Rt△DCF中,CF=.故选A.
9.解析 (1)设A(t,3t-9),则OM=t,AM=3t-9,
∵OA=5,∴t2+(3t-9)2=52,
解得t=4或t=1.4,
∴A(4,3)或A(1.4,-4.8)(不合题意,舍去),
把A(4,3)代入y=,得3=,∴m=12,
∴反比例函数的解析式为y=.
(2)在y=3x-9中,令y=0,得0=3x-9,
解得x=3,∴B(3,0),∴OB=3.
由(1)知A(4,3),∴OM=4,AM=3,
∴BM=OM-OB=4-3=1,
∴tan∠BAM=.
∵∠ANO=∠NOM=∠OMA=90°,∴∠MAN=90°,
∵∠BAE=45°,∴∠BAM+∠NAE=45°.
由当α+β=45°时,若tan α=,则tan β=可得
tan∠NAE=.
(3)由(2)知tan∠NAE=.
∵A(4,3),∴AN=4,ON=3,
∴,∴NE=2,
∴OE=ON-NE=3-2=1,∴E(0,1),
设直线AE的解析式为y=kx+b,
把A(4,3),E(0,1)代入,
得
∴直线AE的解析式为y=x+1.
10.
解析 如图,在AB上截取AQ=1,连接AP,PQ,CQ,∵点E,F分别是边AB,AC的中点,点P是以A为圆心,以AE长为半径的圆弧上的动点,∴,∵∠PAQ=∠BAP,∴△APQ∽△ABP,∴PQ=PB+PC=PQ+PC≥CQ,在Rt△ACQ中,AC=4,AQ=1,∴QC=PB+PC的最小值为.
11.5
解析 如图,连接PB,在BC上取一点E,使得BE=1.∵PB2=4,BE·BC=4,∴PB2=BE·BC,∴,∵∠PBE=∠CBP,∴△PBE∽△CBP,∴PC=PD+PE,∵PE+PD≥DE,在Rt△DCE中,DE=PC的最小值为5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
