2024人教版数学九年级下学期课时练--专项素养综合全练(一)反比例函数与一次函数的综合运用(含解析)
文档属性
| 名称 | 2024人教版数学九年级下学期课时练--专项素养综合全练(一)反比例函数与一次函数的综合运用(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 456.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 11:20:14 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024人教版数学九年级下学期
专项素养综合全练(一)
反比例函数与一次函数的综合运用
类型一 图象共存问题
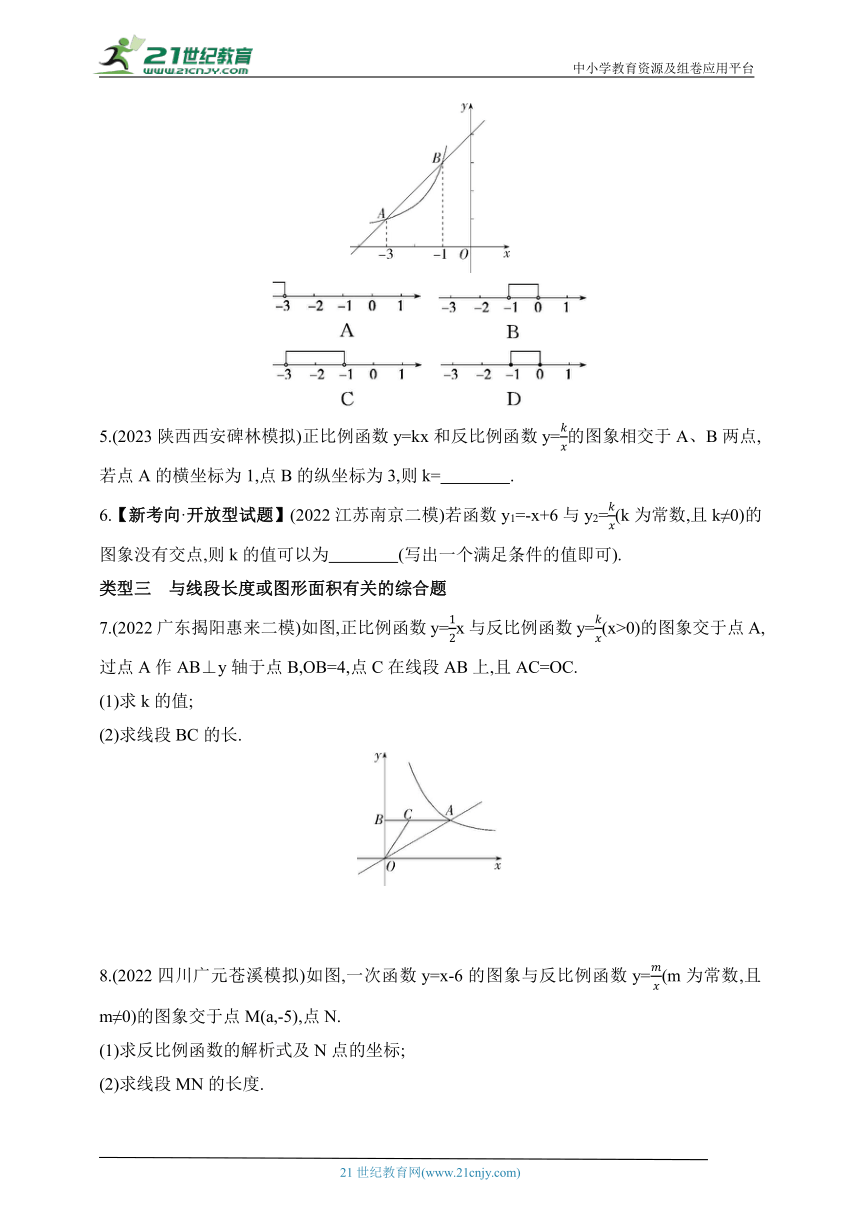
1.(2023福建泉州安溪期中)已知k≠0,函数y=kx-1与y=在同一个平面直角坐标系中的图象可能是( )
2.(2023山东泰安中考)一次函数y=ax+b与反比例函数y=(a,b为常数且均不等于0)在同一坐标系内的图象可能是( )
类型二 图象交点问题
3.(2023福建泉州丰泽期中)点A(a,b)为函数y=与y=x+4的图象的交点,则的值为( )
A.1 B.4 C.-1 D.-4
4.【数形结合思想】(2022云南红河个旧二模)如图,反比例函数y=(x<0)与一次函数y=x+4的图象交于A、B两点,A、B两点的横坐标分别为-3、-1,则关于x的不等式
5.(2023陕西西安碑林模拟)正比例函数y=kx和反比例函数y=的图象相交于A、B两点,若点A的横坐标为1,点B的纵坐标为3,则k= .
6.【新考向·开放型试题】(2022江苏南京二模)若函数y1=-x+6与y2=(k为常数,且k≠0)的图象没有交点,则k的值可以为 (写出一个满足条件的值即可).
类型三 与线段长度或图形面积有关的综合题
7.(2022广东揭阳惠来二模)如图,正比例函数y=x与反比例函数y=(x>0)的图象交于点A,过点A作AB⊥y轴于点B,OB=4,点C在线段AB上,且AC=OC.
(1)求k的值;
(2)求线段BC的长.
8.(2022四川广元苍溪模拟)如图,一次函数y=x-6的图象与反比例函数y=(m为常数,且m≠0)的图象交于点M(a,-5),点N.
(1)求反比例函数的解析式及N点的坐标;
(2)求线段MN的长度.
9.(2023湖北恩施州中考)如图,在平面直角坐标系xOy中,O为坐标原点,直线y=x+2交y轴于点A,交x轴于点B,与双曲线y=(k≠0)在第一、三象限分别交于C、D两点,且AB=BC,连接CO、DO.
(1)求k的值;
(2)求△CDO的面积.
10.【和差法求面积】(2022四川南充中考)如图,直线AB与双曲线交于A(1,6),B(m,-2)两点,直线BO与双曲线在第一象限交于点C,连接AC.
(1)求直线AB与双曲线的解析式;
(2)求△ABC的面积.
答案全解全析
1.D ∵函数y=kx-1的图象必经过点(0,-1),∴排除A、B选项;选项C,由一次函数的图象可知k>0,由反比例函数的图象可知k<0,两结论矛盾,排除C选项;选项D,由一次函数的图象可知k<0,由反比例函数的图象可知k<0,成立.故选D.
2.D 选项A,一次函数y=ax+b的图象经过第一、二、三象限,则a>0,b>0,∴ab>0;反比例函数y=的图象位于第二、四象限,∴ab<0,矛盾.选项B,一次函数y=ax+b的图象经过第一、二、四象限,则a<0,b>0,∴ab<0;反比例函数y=的图象位于第一、三象限,∴ab>0,矛盾.选项C,一次函数y=ax+b的图象经过第一、三、四象限,则a>0,b<0,∴ab<0;反比例函数y=的图象位于第一、三象限,∴ab>0,矛盾.选项D,一次函数y=ax+b的图象经过第一、二、四象限,则a<0,b>0,∴ab<0;反比例函数y=的图象位于第二、四象限,∴ab<0,成立.故选D.
3.A ∵点A(a,b)是反比例函数y=与一次函数y=x+4的图象的交点,∴b==1.故选A.
4.C 由题图可知当-35.-3
解析 ∵正比例函数y=kx与反比例函数y=的图象相交于A、B两点,∴A、B关于原点对称,又∵点A的横坐标为1,点B的纵坐标为3,∴点A的纵坐标是-3,点B的横坐标是-1.∴A(1,-3),B(-1,3).∵反比例函数y=的图象过点A,∴k=1×(-3)=-3.
6.10(答案不唯一,k>9即可)
解析 ∵函数y1=-x+6的图象经过第一、二、四象限,函数y1=-x+6与y2=(k为常数,且k≠0)的图象没有交点,∴反比例函数的图象在第一、三象限,∴k>0,令-x+6=,整理得x2-6x+k=0,两图象无交点,则Δ<0,即(-6)2-4k<0,∴k>9,∴k的值只要是大于9的实数都可以,例如10.
7.解析 (1)∵AB⊥y轴,OB=4,
∴点B的坐标为(0,4),点A的纵坐标是4,
∵点A在正比例函数y=x的图象上,
∴将y=4代入y=x,得x=8,∴A(8,4).
∵点A在反比例函数y=(x>0)的图象上,
∴k=4×8=32.
(2)设C(c,4),
则OC=,AC=AB-BC=8-c,
∵OC=AC,∴=8-c,解得c=3,
∴BC=3.
8.解析 (1)∵一次函数y=x-6的图象经过点M(a,-5),∴-5=a-6,解得a=1,∴M(1,-5).
∵反比例函数y=的图象过点M(1,-5),
∴m=1×(-5)=-5,
∴反比例函数的解析式为y=-.
联立
∴点N的坐标为(5,-1).
(2)如图,过点M作直线平行于y轴,过点N作直线平行于x轴,设两直线交于点P.
∵M(1,-5),N(5,-1),∴PM=4,PN=4.
在Rt△PMN中,MN=.
9.解析 (1)在y=x+2中,令x=0,得y=2,令y=0,得x=-2,∴A(0,2),B(-2,0).
∵AB=BC,∴A为BC的中点,∴C(2,4).
把C(2,4)代入y=,得4=,解得k=8.
∴k的值为8.
(2)解方程组
∴D(-4,-2),
∴S△DOC=S△DOB+S△COB=×2×4=2+4=6,
∴△CDO的面积是6.
10.解析 (1)设双曲线的解析式为y=,
∵点A(1,6)在该双曲线上,∴6=,解得k=6,
∴双曲线的解析式为y=.
∵B(m,-2)在双曲线y=上,∴-2=,
解得m=-3,
∴点B的坐标为(-3,-2).
设直线AB的解析式为y=ax+b,
则
∴直线AB的解析式为y=2x+4.
(2)如图,BE∥y轴∥FG,BG∥x轴∥EF,且EF过点A,FG过点C.
设直线BO的解析式为y=a1x,
∵点B(-3,-2),∴-2=-3a1,解得a1=,
∴直线BO的解析式为y=x,
联立
∴点C的坐标为(3,2),
∵A(1,6),B(-3,-2),C(3,2),
∴EB=8,BG=6,CG=4,CF=4,AF=2,AE=4,
∴S△ABC=S矩形EBGF-S△AEB-S△BGC-S△AFC=8×6-=48-16-12-4=16.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版数学九年级下学期
专项素养综合全练(一)
反比例函数与一次函数的综合运用
类型一 图象共存问题
1.(2023福建泉州安溪期中)已知k≠0,函数y=kx-1与y=在同一个平面直角坐标系中的图象可能是( )
2.(2023山东泰安中考)一次函数y=ax+b与反比例函数y=(a,b为常数且均不等于0)在同一坐标系内的图象可能是( )
类型二 图象交点问题
3.(2023福建泉州丰泽期中)点A(a,b)为函数y=与y=x+4的图象的交点,则的值为( )
A.1 B.4 C.-1 D.-4
4.【数形结合思想】(2022云南红河个旧二模)如图,反比例函数y=(x<0)与一次函数y=x+4的图象交于A、B两点,A、B两点的横坐标分别为-3、-1,则关于x的不等式
5.(2023陕西西安碑林模拟)正比例函数y=kx和反比例函数y=的图象相交于A、B两点,若点A的横坐标为1,点B的纵坐标为3,则k= .
6.【新考向·开放型试题】(2022江苏南京二模)若函数y1=-x+6与y2=(k为常数,且k≠0)的图象没有交点,则k的值可以为 (写出一个满足条件的值即可).
类型三 与线段长度或图形面积有关的综合题
7.(2022广东揭阳惠来二模)如图,正比例函数y=x与反比例函数y=(x>0)的图象交于点A,过点A作AB⊥y轴于点B,OB=4,点C在线段AB上,且AC=OC.
(1)求k的值;
(2)求线段BC的长.
8.(2022四川广元苍溪模拟)如图,一次函数y=x-6的图象与反比例函数y=(m为常数,且m≠0)的图象交于点M(a,-5),点N.
(1)求反比例函数的解析式及N点的坐标;
(2)求线段MN的长度.
9.(2023湖北恩施州中考)如图,在平面直角坐标系xOy中,O为坐标原点,直线y=x+2交y轴于点A,交x轴于点B,与双曲线y=(k≠0)在第一、三象限分别交于C、D两点,且AB=BC,连接CO、DO.
(1)求k的值;
(2)求△CDO的面积.
10.【和差法求面积】(2022四川南充中考)如图,直线AB与双曲线交于A(1,6),B(m,-2)两点,直线BO与双曲线在第一象限交于点C,连接AC.
(1)求直线AB与双曲线的解析式;
(2)求△ABC的面积.
答案全解全析
1.D ∵函数y=kx-1的图象必经过点(0,-1),∴排除A、B选项;选项C,由一次函数的图象可知k>0,由反比例函数的图象可知k<0,两结论矛盾,排除C选项;选项D,由一次函数的图象可知k<0,由反比例函数的图象可知k<0,成立.故选D.
2.D 选项A,一次函数y=ax+b的图象经过第一、二、三象限,则a>0,b>0,∴ab>0;反比例函数y=的图象位于第二、四象限,∴ab<0,矛盾.选项B,一次函数y=ax+b的图象经过第一、二、四象限,则a<0,b>0,∴ab<0;反比例函数y=的图象位于第一、三象限,∴ab>0,矛盾.选项C,一次函数y=ax+b的图象经过第一、三、四象限,则a>0,b<0,∴ab<0;反比例函数y=的图象位于第一、三象限,∴ab>0,矛盾.选项D,一次函数y=ax+b的图象经过第一、二、四象限,则a<0,b>0,∴ab<0;反比例函数y=的图象位于第二、四象限,∴ab<0,成立.故选D.
3.A ∵点A(a,b)是反比例函数y=与一次函数y=x+4的图象的交点,∴b==1.故选A.
4.C 由题图可知当-3
解析 ∵正比例函数y=kx与反比例函数y=的图象相交于A、B两点,∴A、B关于原点对称,又∵点A的横坐标为1,点B的纵坐标为3,∴点A的纵坐标是-3,点B的横坐标是-1.∴A(1,-3),B(-1,3).∵反比例函数y=的图象过点A,∴k=1×(-3)=-3.
6.10(答案不唯一,k>9即可)
解析 ∵函数y1=-x+6的图象经过第一、二、四象限,函数y1=-x+6与y2=(k为常数,且k≠0)的图象没有交点,∴反比例函数的图象在第一、三象限,∴k>0,令-x+6=,整理得x2-6x+k=0,两图象无交点,则Δ<0,即(-6)2-4k<0,∴k>9,∴k的值只要是大于9的实数都可以,例如10.
7.解析 (1)∵AB⊥y轴,OB=4,
∴点B的坐标为(0,4),点A的纵坐标是4,
∵点A在正比例函数y=x的图象上,
∴将y=4代入y=x,得x=8,∴A(8,4).
∵点A在反比例函数y=(x>0)的图象上,
∴k=4×8=32.
(2)设C(c,4),
则OC=,AC=AB-BC=8-c,
∵OC=AC,∴=8-c,解得c=3,
∴BC=3.
8.解析 (1)∵一次函数y=x-6的图象经过点M(a,-5),∴-5=a-6,解得a=1,∴M(1,-5).
∵反比例函数y=的图象过点M(1,-5),
∴m=1×(-5)=-5,
∴反比例函数的解析式为y=-.
联立
∴点N的坐标为(5,-1).
(2)如图,过点M作直线平行于y轴,过点N作直线平行于x轴,设两直线交于点P.
∵M(1,-5),N(5,-1),∴PM=4,PN=4.
在Rt△PMN中,MN=.
9.解析 (1)在y=x+2中,令x=0,得y=2,令y=0,得x=-2,∴A(0,2),B(-2,0).
∵AB=BC,∴A为BC的中点,∴C(2,4).
把C(2,4)代入y=,得4=,解得k=8.
∴k的值为8.
(2)解方程组
∴D(-4,-2),
∴S△DOC=S△DOB+S△COB=×2×4=2+4=6,
∴△CDO的面积是6.
10.解析 (1)设双曲线的解析式为y=,
∵点A(1,6)在该双曲线上,∴6=,解得k=6,
∴双曲线的解析式为y=.
∵B(m,-2)在双曲线y=上,∴-2=,
解得m=-3,
∴点B的坐标为(-3,-2).
设直线AB的解析式为y=ax+b,
则
∴直线AB的解析式为y=2x+4.
(2)如图,BE∥y轴∥FG,BG∥x轴∥EF,且EF过点A,FG过点C.
设直线BO的解析式为y=a1x,
∵点B(-3,-2),∴-2=-3a1,解得a1=,
∴直线BO的解析式为y=x,
联立
∴点C的坐标为(3,2),
∵A(1,6),B(-3,-2),C(3,2),
∴EB=8,BG=6,CG=4,CF=4,AF=2,AE=4,
∴S△ABC=S矩形EBGF-S△AEB-S△BGC-S△AFC=8×6-=48-16-12-4=16.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
