2024人教版数学九年级下学期课时练--专项素养综合全练(三)相似三角形的判定的模型(含解析)
文档属性
| 名称 | 2024人教版数学九年级下学期课时练--专项素养综合全练(三)相似三角形的判定的模型(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 11:21:09 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024人教版数学九年级下学期
专项素养综合全练(三)
相似三角形的判定的模型
模型一 “A”字型
1.(2023湖北恩施州中考)如图,在△ABC中,DE∥BC分别交AC,AB于点D,E,EF∥AC交BC于点F,,BF=8,则DE的长为( )
A. C.2 D.3
2.(2023北京房山二模)如图,△ABC中,CD平分∠ACB,DE∥AC交BC于点E.若AC=5,DE=3,则BE= .
3.(2021广东深圳光明模拟)如图,在平行四边形ABCD中,对角线AC,BD交于点O.过点O作BD的垂线,交BA的延长线于点E,交AD于点F,交BC于点N,若EF=OF,∠CBD=30°,BD=6.
(1)求证:EF=EN;
(2)求AF的长.
模型二 “8”字型
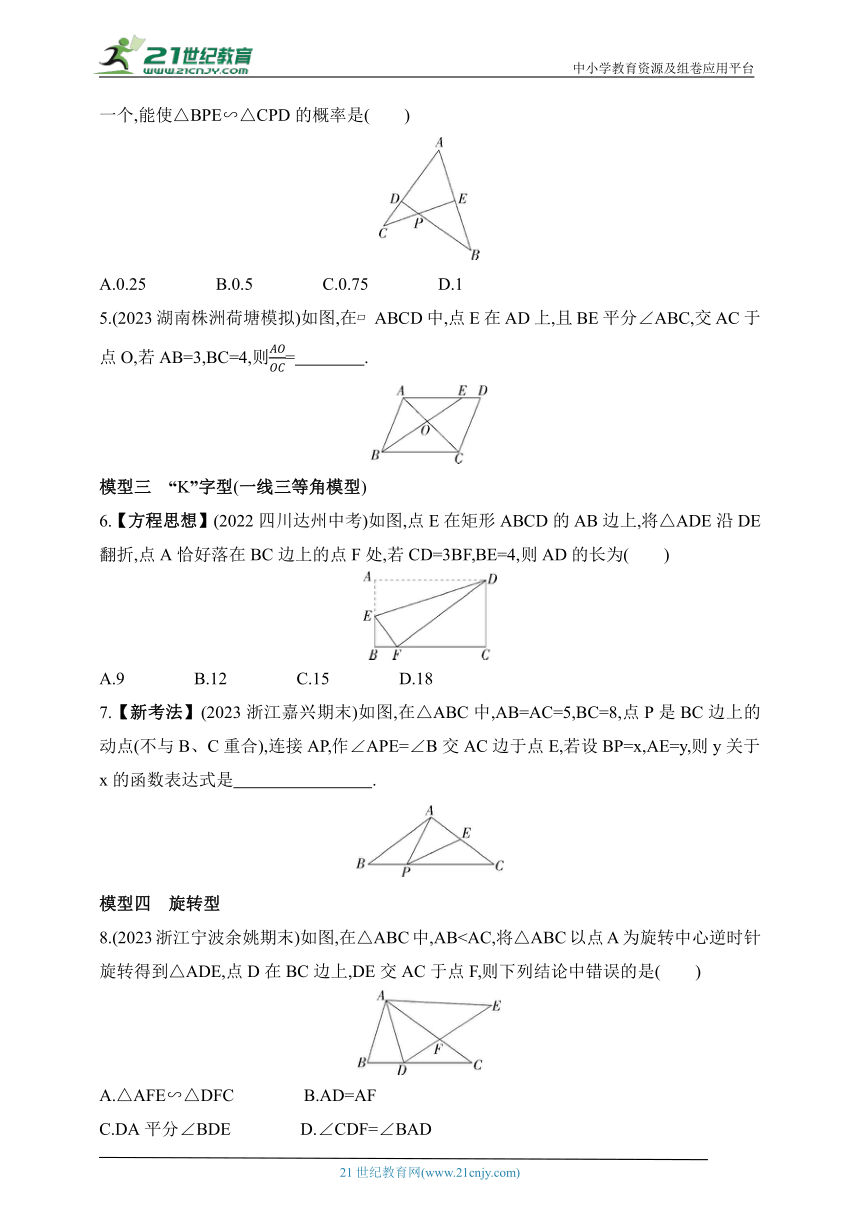
4.【新考法】(2022江苏扬州高邮期末)如图,在下列四个条件:①∠B=∠C,②∠ADB=∠AEC,③AD∶AC=AE∶AB,④PE∶PD=PB∶PC中,随机抽取一个,能使△BPE∽△CPD的概率是( )
A.0.25 B.0.5 C.0.75 D.1
5.(2023湖南株洲荷塘模拟)如图,在 ABCD中,点E在AD上,且BE平分∠ABC,交AC于点O,若AB=3,BC=4,则= .
模型三 “K”字型(一线三等角模型)
6.【方程思想】(2022四川达州中考)如图,点E在矩形ABCD的AB边上,将△ADE沿DE翻折,点A恰好落在BC边上的点F处,若CD=3BF,BE=4,则AD的长为( )
A.9 B.12 C.15 D.18
7.【新考法】(2023浙江嘉兴期末)如图,在△ABC中,AB=AC=5,BC=8,点P是BC边上的动点(不与B、C重合),连接AP,作∠APE=∠B交AC边于点E,若设BP=x,AE=y,则y关于x的函数表达式是 .
模型四 旋转型
8.(2023浙江宁波余姚期末)如图,在△ABC中,ABA.△AFE∽△DFC B.AD=AF
C.DA平分∠BDE D.∠CDF=∠BAD
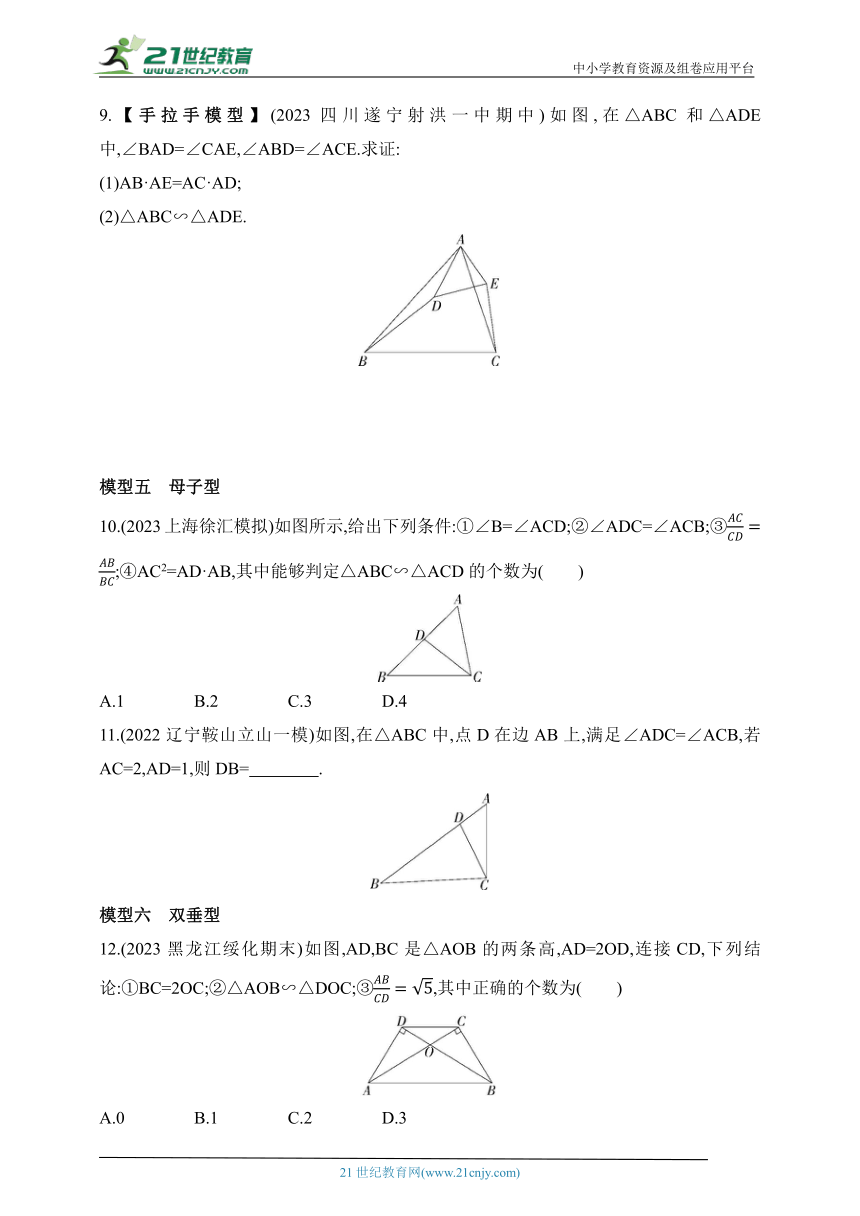
9.【手拉手模型】(2023四川遂宁射洪一中期中)如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABD=∠ACE.求证:
(1)AB·AE=AC·AD;
(2)△ABC∽△ADE.
模型五 母子型
10.(2023上海徐汇模拟)如图所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③;④AC2=AD·AB,其中能够判定△ABC∽△ACD的个数为( )
A.1 B.2 C.3 D.4
11.(2022辽宁鞍山立山一模)如图,在△ABC中,点D在边AB上,满足∠ADC=∠ACB,若AC=2,AD=1,则DB= .
模型六 双垂型
12.(2023黑龙江绥化期末)如图,AD,BC是△AOB的两条高,AD=2OD,连接CD,下列结论:①BC=2OC;②△AOB∽△DOC;③,其中正确的个数为( )
A.0 B.1 C.2 D.3
13.(2021湖南常德汉寿月考)如图,AD为直角三角形ABC斜边上的高,DE⊥AB于点E,图中相似三角形共有 对.
答案全解全析
1.A ∵DE∥BC,EF∥AC,∴四边形EFCD是平行四边形,∴DE=CF,设DE=CF=x,∵BF=8,∴BC=BF+CF=8+x,∵DE∥BC,∴△AED∽△ABC,∴,即,解得x=,即DE的长为,故选A.
2.
解析 ∵CD平分∠ACB,∴∠ACD=∠DCE,∵DE∥AC,∴∠ACD=∠CDE,∴∠CDE=∠DCE,∴DE=CE=3,∵DE∥AC,∴△BDE∽△BAC,∴.
3.解析 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AO=OC,BO=OD,∴∠DAO=∠BCO.
在△AOF与△CON中,
∴△AOF≌△CON(ASA),∴OF=ON.
又∵EF=OF,∴EF=EN.
(2)∵EF⊥BD,∴∠BON=90°.
∵∠OBN=30°,BO=,
∴BN=2ON,根据勾股定理可得ON=3,BN=6.
∵AF∥BN,∴△EAF∽△EBN,
∴,∴AF=2.
4.C 本题综合考查了相似三角形的判定与概率的求解.
①∵∠B=∠C,∠EPB=∠DPC,∴△BPE∽△CPD;
②∵∠ADB=∠AEC,∴∠PDC=∠PEB,
又∵∠DPC=∠EPB,∴△CPD∽△BPE;
③由AD∶AC=AE∶AB和题图中条件无法得出△BPE∽△CPD(由AD∶AB=AE∶AC和题图中条件才能得出△BPE∽△CPD);
④∵PE∶PD=PB∶PC,∠EPB=∠DPC,
∴△BPE∽△CPD,
∴在四个条件中,随机抽取一个,能使△BPE∽△CPD的概率是0.75.故选C.
5.
解析 ∵在 ABCD中,AD∥BC,∴∠AEB=∠CBE,∵BE平分∠ABC,∴∠ABE=∠CBE,∴∠AEB=∠ABE,∴AE=AB=3,∵AD∥BC,∴△AOE∽△COB,∴.
6.C ∵四边形ABCD是矩形,∴AD=BC,∠A=∠B=∠C=90°.∵将矩形ABCD沿DE翻折,∴AD=DF=BC,∠A=∠DFE=90°,∴∠BFE+∠DFC=∠BFE+∠BEF=90°,∴∠BEF=∠CFD,∴△BEF∽△CFD,∴,∵CD=3BF,∴CF=3BE=12,设BF=x,则CD=3x,DF=BC=x+12,∵∠C=90°,∴Rt△CDF中,CD2+CF2=DF2,∴(3x)2+122=(x+12)2,解得x=3(舍去x=0),∴AD=DF=3+12=15.故选C.
7.y=x+5(0解析 本题综合考查相似三角形的判定与性质及确定函数解析式.∵∠APC=∠APE+∠EPC=∠BAP+∠B,∠APE=∠B,∴∠EPC=∠BAP.∵AB=AC,∴∠B=∠C,∴△ABP∽△PCE,∴x+5(08.B ∵将△ABC以点A为旋转中心逆时针旋转得到△ADE,∴∠BAC=∠DAE,∠B=∠ADE,AB=AD,∠E=∠C,∴∠B=∠ADB,∴∠ADB=∠ADE,∴DA平分∠BDE,故C正确;∵∠AFE=∠CFD,∠E=∠C,∴△AFE∽△DFC,故A正确;∵△AFE∽△DFC,∴∠CDF=∠CAE,∵∠BAC=∠DAE,∴∠BAD=∠CAE,∴∠CDF=∠BAD,故D正确;没有条件可以证明∠ADF=∠AFD,即不能判定AD=AF.故选B.
9.证明 (1)∵∠BAD=∠CAE,∠ABD=∠ACE,
∴△ABD∽△ACE,∴,
∴AB·AE=AC·AD.
(2)∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠DAC+∠CAE,
即∠BAC=∠DAE,
∵,
∴△ABC∽△ADE.
模型解读 手拉手模型:顶角相等且顶角的顶点重合的两个等腰三角形组成手拉手全等模型(如图1);一对对应角顶点重合的两个相似三角形组成手拉手相似模型(如图2).
10.C ①∵∠B=∠ACD,∠DAC=∠BAC,∴△ABC∽△ACD,故①符合题意;②∵∠ADC=∠ACB,∠DAC=∠BAC,∴△ABC∽△ACD,故②符合题意;③,但∠ACD和∠ABC不一定相等,因此不能判定△ABC∽△ACD,故③不符合题意;④∵AC2=AD·AB,∴,又∵∠DAC=∠BAC,∴△ABC∽△ACD,故④符合题意.综上所述,能够判定△ABC∽△ACD的条件的个数为3.故选C.
11.3
解析 在△ACD和△ABC中,∵∠ADC=∠ACB,∠A是公共角,∴△ACD∽△ABC,∴,∵AC=2,AD=1,∴AB=4,∴DB=AB-AD=4-1=3.
12.D ∵AD,BC是△AOB的两条高,∴∠ADO=∠BCO=90°,又∵∠AOD=∠BOC,∴△AOD∽△BOC,∴=2,∴BC=2OC,故①正确;∵,又∵∠AOB=∠DOC,∴△AOB∽△DOC,故②正确;∵△AOB∽△DOC,∴,设OD=x,则AD=2x,∴AO=,故③正确.综上所述,正确的个数为3.
故选D.
13.10
解析 ∵AD是Rt△ABC斜边上的高,DE⊥AB,
∴∠AED=∠ADC=∠BED=∠ADB=∠CAB=90°.
∵∠C=∠C,∠B=∠B,∴△ACD∽△BCA∽△BDE∽△BAD,
∵∠DAE=∠BAD,
∴△DAE∽△BAD,
∴△ACD∽△BCA∽△BDE∽△BAD∽△DAE,
∴题图中共有10对相似三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版数学九年级下学期
专项素养综合全练(三)
相似三角形的判定的模型
模型一 “A”字型
1.(2023湖北恩施州中考)如图,在△ABC中,DE∥BC分别交AC,AB于点D,E,EF∥AC交BC于点F,,BF=8,则DE的长为( )
A. C.2 D.3
2.(2023北京房山二模)如图,△ABC中,CD平分∠ACB,DE∥AC交BC于点E.若AC=5,DE=3,则BE= .
3.(2021广东深圳光明模拟)如图,在平行四边形ABCD中,对角线AC,BD交于点O.过点O作BD的垂线,交BA的延长线于点E,交AD于点F,交BC于点N,若EF=OF,∠CBD=30°,BD=6.
(1)求证:EF=EN;
(2)求AF的长.
模型二 “8”字型
4.【新考法】(2022江苏扬州高邮期末)如图,在下列四个条件:①∠B=∠C,②∠ADB=∠AEC,③AD∶AC=AE∶AB,④PE∶PD=PB∶PC中,随机抽取一个,能使△BPE∽△CPD的概率是( )
A.0.25 B.0.5 C.0.75 D.1
5.(2023湖南株洲荷塘模拟)如图,在 ABCD中,点E在AD上,且BE平分∠ABC,交AC于点O,若AB=3,BC=4,则= .
模型三 “K”字型(一线三等角模型)
6.【方程思想】(2022四川达州中考)如图,点E在矩形ABCD的AB边上,将△ADE沿DE翻折,点A恰好落在BC边上的点F处,若CD=3BF,BE=4,则AD的长为( )
A.9 B.12 C.15 D.18
7.【新考法】(2023浙江嘉兴期末)如图,在△ABC中,AB=AC=5,BC=8,点P是BC边上的动点(不与B、C重合),连接AP,作∠APE=∠B交AC边于点E,若设BP=x,AE=y,则y关于x的函数表达式是 .
模型四 旋转型
8.(2023浙江宁波余姚期末)如图,在△ABC中,AB
C.DA平分∠BDE D.∠CDF=∠BAD
9.【手拉手模型】(2023四川遂宁射洪一中期中)如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABD=∠ACE.求证:
(1)AB·AE=AC·AD;
(2)△ABC∽△ADE.
模型五 母子型
10.(2023上海徐汇模拟)如图所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③;④AC2=AD·AB,其中能够判定△ABC∽△ACD的个数为( )
A.1 B.2 C.3 D.4
11.(2022辽宁鞍山立山一模)如图,在△ABC中,点D在边AB上,满足∠ADC=∠ACB,若AC=2,AD=1,则DB= .
模型六 双垂型
12.(2023黑龙江绥化期末)如图,AD,BC是△AOB的两条高,AD=2OD,连接CD,下列结论:①BC=2OC;②△AOB∽△DOC;③,其中正确的个数为( )
A.0 B.1 C.2 D.3
13.(2021湖南常德汉寿月考)如图,AD为直角三角形ABC斜边上的高,DE⊥AB于点E,图中相似三角形共有 对.
答案全解全析
1.A ∵DE∥BC,EF∥AC,∴四边形EFCD是平行四边形,∴DE=CF,设DE=CF=x,∵BF=8,∴BC=BF+CF=8+x,∵DE∥BC,∴△AED∽△ABC,∴,即,解得x=,即DE的长为,故选A.
2.
解析 ∵CD平分∠ACB,∴∠ACD=∠DCE,∵DE∥AC,∴∠ACD=∠CDE,∴∠CDE=∠DCE,∴DE=CE=3,∵DE∥AC,∴△BDE∽△BAC,∴.
3.解析 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AO=OC,BO=OD,∴∠DAO=∠BCO.
在△AOF与△CON中,
∴△AOF≌△CON(ASA),∴OF=ON.
又∵EF=OF,∴EF=EN.
(2)∵EF⊥BD,∴∠BON=90°.
∵∠OBN=30°,BO=,
∴BN=2ON,根据勾股定理可得ON=3,BN=6.
∵AF∥BN,∴△EAF∽△EBN,
∴,∴AF=2.
4.C 本题综合考查了相似三角形的判定与概率的求解.
①∵∠B=∠C,∠EPB=∠DPC,∴△BPE∽△CPD;
②∵∠ADB=∠AEC,∴∠PDC=∠PEB,
又∵∠DPC=∠EPB,∴△CPD∽△BPE;
③由AD∶AC=AE∶AB和题图中条件无法得出△BPE∽△CPD(由AD∶AB=AE∶AC和题图中条件才能得出△BPE∽△CPD);
④∵PE∶PD=PB∶PC,∠EPB=∠DPC,
∴△BPE∽△CPD,
∴在四个条件中,随机抽取一个,能使△BPE∽△CPD的概率是0.75.故选C.
5.
解析 ∵在 ABCD中,AD∥BC,∴∠AEB=∠CBE,∵BE平分∠ABC,∴∠ABE=∠CBE,∴∠AEB=∠ABE,∴AE=AB=3,∵AD∥BC,∴△AOE∽△COB,∴.
6.C ∵四边形ABCD是矩形,∴AD=BC,∠A=∠B=∠C=90°.∵将矩形ABCD沿DE翻折,∴AD=DF=BC,∠A=∠DFE=90°,∴∠BFE+∠DFC=∠BFE+∠BEF=90°,∴∠BEF=∠CFD,∴△BEF∽△CFD,∴,∵CD=3BF,∴CF=3BE=12,设BF=x,则CD=3x,DF=BC=x+12,∵∠C=90°,∴Rt△CDF中,CD2+CF2=DF2,∴(3x)2+122=(x+12)2,解得x=3(舍去x=0),∴AD=DF=3+12=15.故选C.
7.y=x+5(0
9.证明 (1)∵∠BAD=∠CAE,∠ABD=∠ACE,
∴△ABD∽△ACE,∴,
∴AB·AE=AC·AD.
(2)∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠DAC+∠CAE,
即∠BAC=∠DAE,
∵,
∴△ABC∽△ADE.
模型解读 手拉手模型:顶角相等且顶角的顶点重合的两个等腰三角形组成手拉手全等模型(如图1);一对对应角顶点重合的两个相似三角形组成手拉手相似模型(如图2).
10.C ①∵∠B=∠ACD,∠DAC=∠BAC,∴△ABC∽△ACD,故①符合题意;②∵∠ADC=∠ACB,∠DAC=∠BAC,∴△ABC∽△ACD,故②符合题意;③,但∠ACD和∠ABC不一定相等,因此不能判定△ABC∽△ACD,故③不符合题意;④∵AC2=AD·AB,∴,又∵∠DAC=∠BAC,∴△ABC∽△ACD,故④符合题意.综上所述,能够判定△ABC∽△ACD的条件的个数为3.故选C.
11.3
解析 在△ACD和△ABC中,∵∠ADC=∠ACB,∠A是公共角,∴△ACD∽△ABC,∴,∵AC=2,AD=1,∴AB=4,∴DB=AB-AD=4-1=3.
12.D ∵AD,BC是△AOB的两条高,∴∠ADO=∠BCO=90°,又∵∠AOD=∠BOC,∴△AOD∽△BOC,∴=2,∴BC=2OC,故①正确;∵,又∵∠AOB=∠DOC,∴△AOB∽△DOC,故②正确;∵△AOB∽△DOC,∴,设OD=x,则AD=2x,∴AO=,故③正确.综上所述,正确的个数为3.
故选D.
13.10
解析 ∵AD是Rt△ABC斜边上的高,DE⊥AB,
∴∠AED=∠ADC=∠BED=∠ADB=∠CAB=90°.
∵∠C=∠C,∠B=∠B,∴△ACD∽△BCA∽△BDE∽△BAD,
∵∠DAE=∠BAD,
∴△DAE∽△BAD,
∴△ACD∽△BCA∽△BDE∽△BAD∽△DAE,
∴题图中共有10对相似三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
