2024人教版数学九年级下学期课时练--专项素养综合全练(四)相似三角形的判定与性质的综合应用(含解析)
文档属性
| 名称 | 2024人教版数学九年级下学期课时练--专项素养综合全练(四)相似三角形的判定与性质的综合应用(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 463.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 11:21:56 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024人教版数学九年级下学期
专项素养综合全练(四)
相似三角形的判定与性质的综合应用
类型一 求线段长
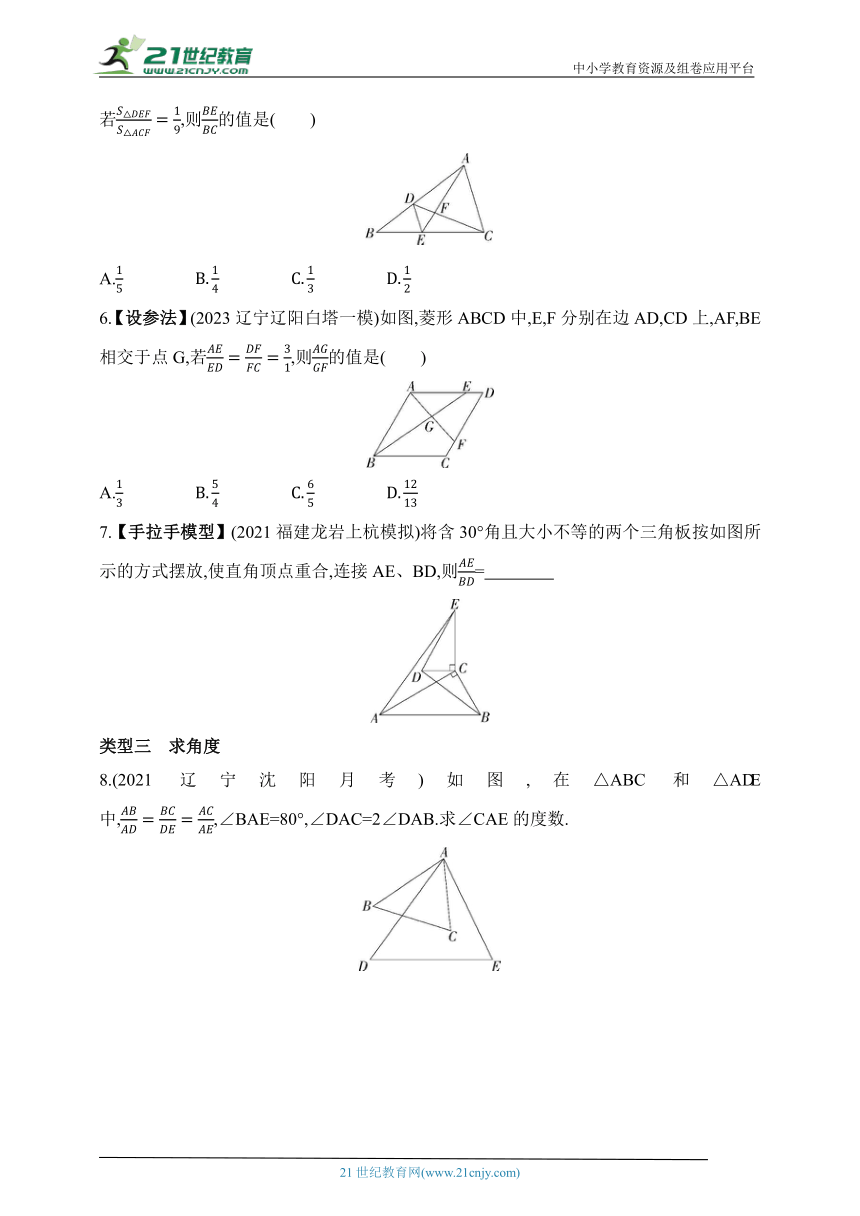
1.【8字模型】(2023陕西中考)如图,DE是△ABC 的中位线,点F在DB上,DF=2BF,连接EF并延长,与CB的延长线相交于点M.若BC=6,则线段CM的长为( )
A. D.8
2.【三垂直模型】(2023安徽淮北月考)如图,在矩形ABCD中,AB=4,BC=6,点E是BC边的中点,连接AE,过点E作EF⊥AE交CD于点F,连接AF,则AF的长为( )
A.
3.(2022甘肃武威中考)如图,在矩形ABCD中,AB=6 cm,BC=9 cm,点E,F分别在边AB,BC上,AE=2 cm,BD,EF交于点G,若G是EF的中点,则BG的长为 cm.
4.(2023山西晋中模拟)如图,在菱形ABCD中,AB=10,对角线BD=16,过点C作CE⊥AD于点E,CE与BD交于点F,则EF的长为 .
类型二 求比值
5.(2023广东广州增城二模)如图,点D,E都是△ABC边上的点,DE∥AC,AE交DC于点F,若,则的值是( )
A.
6.【设参法】(2023辽宁辽阳白塔一模)如图,菱形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若,则的值是( )
A.
7.【手拉手模型】(2021福建龙岩上杭模拟)将含30°角且大小不等的两个三角板按如图所示的方式摆放,使直角顶点重合,连接AE、BD,则=
类型三 求角度
8.(2021辽宁沈阳月考)如图,在△ABC和△ADE中,,∠BAE=80°,∠DAC=2∠DAB.求∠CAE的度数.
9.如图,在△ABC中,AB=AC,AB⊥AC,点D是AC的中点,AE⊥BD于点E.(M9227004)
(1)求证:AD2=DE·BD;
(2)求证:△DEC∽△DCB;
(3)求∠AEC的大小.
类型四 证明比例式或等积式
10.(2022山东滨州中考)如图,已知AC为☉O的直径,直线PA与☉O相切于点A,直线PD经过☉O上的点B且∠CBD=∠CAB,连接OP交AB于点M.
求证:(1)PD是☉O的切线;
(2)AM2=OM·PM.
11.【一题多解】(2023上海杨浦期末)已知等腰△ABC中,AB=AC,点D、E分别是边BC、AC上的点,且CD=3BD,连接AD、BE,交点为F.
(1)若AF=4DF,求的值;
(2)若BD2=DF·AD,求证:BC2=4CE·AC.
答案全解全析
1.C ∵DE是△ABC的中位线,∴DE∥BC,DE=×6=3,∴△DEF∽△BMF,∴.故选C.
2.A ∵四边形ABCD是矩形,AB=4,BC=6,∴AB=CD=4,BC=AD=6,∠D=∠C=∠B=90°,∵点E是BC边的中点,∴BE=EC=3.∵EF⊥AE,∴∠AEF=90°,∴∠AEB+∠FEC=90°,又∵∠EAB+∠AEB=90°,∴∠EAB=∠FEC,∴△ABE∽△ECF,∴.故选A.
3.
解析 ∵四边形ABCD是矩形,∴CD=AB=6 cm,∠ABC=∠C=90°,AB∥CD,∴∠ABD=∠BDC.∵AE=2 cm,∴BE=AB-AE=6-2=4(cm).∵G是EF的中点,∴EG=BG=EF,∴∠BEG=∠ABD,∴∠BEG=∠BDC,∴△EBF∽△DCB,∴,∴BF=6 cm,∴EF=(cm).
4.
解析 如图,连接AC交BD于点O,∵四边形ABCD是菱形,∴AB=AD=CD=10,AC⊥BD,OB=OD==6,∴AC=12.∵CE⊥AD,∴菱形ABCD的面积=AD·CE=AC·BD,∴10CE=,∵∠DEF=∠DOA=90°,∠EDF=∠ODA,∴△EDF∽△ODA,∴.
5.C ∵DE∥AC,∴△DEF∽△CAF,∵.∵点D,E都是△ABC边上的点,DE∥AC,∴△DEB∽△ACB,∴.故选C.
6.D 如图,延长BE交CD延长线于M,∵四边形ABCD是菱形,∴AD=CD=BC=AB,∵,∴AE=DF,DE=FC.设DE=x,则DF=3x,AD=4x,∵ED∥BC,∴△MED∽△MBC,∴MD∶MC=ED∶BC=1∶4,∴x,∵AB∥MF,∴△ABG∽△FMG,∴.故选D.
7.
解析 ∵△EDC与△ACB中,∠DEC=∠BAC=30°,∠ACB=∠ECD=90°,∴AB=2BC,AC=.∵∠ACB+∠DCA=∠ECD+∠DCA,∴∠DCB=∠ECA,∴△ECA∽△DCB,∴.
8.解析 ∵,∴△ABC∽△ADE,
∴∠BAC=∠DAE,∴∠BAD=∠CAE.
∵∠DAC=2∠DAB=2∠CAE,
∴∠BAE=∠BAC+∠CAE=4∠CAE,
∵∠BAE=80°,∴∠CAE=20°.
9.解析 (1)证明:∵AB⊥AC,AE⊥BD,
∴∠BAD=∠AED=90°,
∵∠ADE=∠BDA,∴△AED∽△BAD,
∴,∴AD2=DE·BD.
(2)证明:∵点D为AC的中点,∴AD=CD,
∵AD2=DE·BD,
∴CD2=DE·BD,∴,
∵∠CDE=∠BDC,∴△DEC∽△DCB.
(3)∵AB⊥AC,AB=AC,
∴△ABC为等腰直角三角形,∠ACB=45°,
∵△DEC∽△DCB,∴∠DEC=∠DCB=45°,
∵AE⊥BD,∴∠AED=90°,
∴∠AEC=∠AED+∠DEC=90°+45°=135°.
10.证明 (1)连接OB,如图所示,
∵OB=OC,
∴∠OCB=∠OBC.
∵AC是☉O的直径,
∴∠CBA=90°,
∴∠CAB+∠OCB=90°.
∵∠CBD=∠CAB,
∴∠CBD+∠OBC=90°,
∴∠OBD=90°,
∴PD是☉O的切线.
(2)由(1)知PD是☉O的切线,
又直线PA与☉O相切,∴PO垂直平分AB,
∴∠AMP=∠AMO=90°,
∴∠APM+∠PAM=90°.
∵∠OAP=90°,∴∠PAM+∠OAM=90°,
∴∠APM=∠OAM,∴△OAM∽△APM,
∴,
∴AM2=OM·PM.
11.解析 (1)解法一:作AG∥BC,交BE延长线于G,
∵AG∥BC,∴△AGF∽△DBF,
∵AF=4DF,∴AG=4BD.
∵CD=3BD,∴BC=4BD,∴AG=BC,
∵AG∥BC,∴△AGE∽△CBE,
∴=1.
解法二:作CH∥AD,交BE延长线于H,
∵CH∥AD,∴△BDF∽△BCH,∴.
∵CD=3BD,∴BC=4BD,∴CH=4DF.
∵AF=4DF,∴AF=CH.
∵CH∥AD,∴△AEF∽△CEH,
∴=1.
(2)证明:∵BD2=DF·AD,∴.
∵∠BDF=∠ADB,∴△BDF∽△ADB,
∴∠BAD=∠FBD.
∵AB=AC,∴∠ABD=∠ACB,
∴△ABD∽△BCE,∴,
∴CE·AB=BD·BC.
又∵AB=AC,BC=BD+CD=4BD,
∴CE·AC=BC·BC,
∴BC2=4CE·AC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版数学九年级下学期
专项素养综合全练(四)
相似三角形的判定与性质的综合应用
类型一 求线段长
1.【8字模型】(2023陕西中考)如图,DE是△ABC 的中位线,点F在DB上,DF=2BF,连接EF并延长,与CB的延长线相交于点M.若BC=6,则线段CM的长为( )
A. D.8
2.【三垂直模型】(2023安徽淮北月考)如图,在矩形ABCD中,AB=4,BC=6,点E是BC边的中点,连接AE,过点E作EF⊥AE交CD于点F,连接AF,则AF的长为( )
A.
3.(2022甘肃武威中考)如图,在矩形ABCD中,AB=6 cm,BC=9 cm,点E,F分别在边AB,BC上,AE=2 cm,BD,EF交于点G,若G是EF的中点,则BG的长为 cm.
4.(2023山西晋中模拟)如图,在菱形ABCD中,AB=10,对角线BD=16,过点C作CE⊥AD于点E,CE与BD交于点F,则EF的长为 .
类型二 求比值
5.(2023广东广州增城二模)如图,点D,E都是△ABC边上的点,DE∥AC,AE交DC于点F,若,则的值是( )
A.
6.【设参法】(2023辽宁辽阳白塔一模)如图,菱形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若,则的值是( )
A.
7.【手拉手模型】(2021福建龙岩上杭模拟)将含30°角且大小不等的两个三角板按如图所示的方式摆放,使直角顶点重合,连接AE、BD,则=
类型三 求角度
8.(2021辽宁沈阳月考)如图,在△ABC和△ADE中,,∠BAE=80°,∠DAC=2∠DAB.求∠CAE的度数.
9.如图,在△ABC中,AB=AC,AB⊥AC,点D是AC的中点,AE⊥BD于点E.(M9227004)
(1)求证:AD2=DE·BD;
(2)求证:△DEC∽△DCB;
(3)求∠AEC的大小.
类型四 证明比例式或等积式
10.(2022山东滨州中考)如图,已知AC为☉O的直径,直线PA与☉O相切于点A,直线PD经过☉O上的点B且∠CBD=∠CAB,连接OP交AB于点M.
求证:(1)PD是☉O的切线;
(2)AM2=OM·PM.
11.【一题多解】(2023上海杨浦期末)已知等腰△ABC中,AB=AC,点D、E分别是边BC、AC上的点,且CD=3BD,连接AD、BE,交点为F.
(1)若AF=4DF,求的值;
(2)若BD2=DF·AD,求证:BC2=4CE·AC.
答案全解全析
1.C ∵DE是△ABC的中位线,∴DE∥BC,DE=×6=3,∴△DEF∽△BMF,∴.故选C.
2.A ∵四边形ABCD是矩形,AB=4,BC=6,∴AB=CD=4,BC=AD=6,∠D=∠C=∠B=90°,∵点E是BC边的中点,∴BE=EC=3.∵EF⊥AE,∴∠AEF=90°,∴∠AEB+∠FEC=90°,又∵∠EAB+∠AEB=90°,∴∠EAB=∠FEC,∴△ABE∽△ECF,∴.故选A.
3.
解析 ∵四边形ABCD是矩形,∴CD=AB=6 cm,∠ABC=∠C=90°,AB∥CD,∴∠ABD=∠BDC.∵AE=2 cm,∴BE=AB-AE=6-2=4(cm).∵G是EF的中点,∴EG=BG=EF,∴∠BEG=∠ABD,∴∠BEG=∠BDC,∴△EBF∽△DCB,∴,∴BF=6 cm,∴EF=(cm).
4.
解析 如图,连接AC交BD于点O,∵四边形ABCD是菱形,∴AB=AD=CD=10,AC⊥BD,OB=OD==6,∴AC=12.∵CE⊥AD,∴菱形ABCD的面积=AD·CE=AC·BD,∴10CE=,∵∠DEF=∠DOA=90°,∠EDF=∠ODA,∴△EDF∽△ODA,∴.
5.C ∵DE∥AC,∴△DEF∽△CAF,∵.∵点D,E都是△ABC边上的点,DE∥AC,∴△DEB∽△ACB,∴.故选C.
6.D 如图,延长BE交CD延长线于M,∵四边形ABCD是菱形,∴AD=CD=BC=AB,∵,∴AE=DF,DE=FC.设DE=x,则DF=3x,AD=4x,∵ED∥BC,∴△MED∽△MBC,∴MD∶MC=ED∶BC=1∶4,∴x,∵AB∥MF,∴△ABG∽△FMG,∴.故选D.
7.
解析 ∵△EDC与△ACB中,∠DEC=∠BAC=30°,∠ACB=∠ECD=90°,∴AB=2BC,AC=.∵∠ACB+∠DCA=∠ECD+∠DCA,∴∠DCB=∠ECA,∴△ECA∽△DCB,∴.
8.解析 ∵,∴△ABC∽△ADE,
∴∠BAC=∠DAE,∴∠BAD=∠CAE.
∵∠DAC=2∠DAB=2∠CAE,
∴∠BAE=∠BAC+∠CAE=4∠CAE,
∵∠BAE=80°,∴∠CAE=20°.
9.解析 (1)证明:∵AB⊥AC,AE⊥BD,
∴∠BAD=∠AED=90°,
∵∠ADE=∠BDA,∴△AED∽△BAD,
∴,∴AD2=DE·BD.
(2)证明:∵点D为AC的中点,∴AD=CD,
∵AD2=DE·BD,
∴CD2=DE·BD,∴,
∵∠CDE=∠BDC,∴△DEC∽△DCB.
(3)∵AB⊥AC,AB=AC,
∴△ABC为等腰直角三角形,∠ACB=45°,
∵△DEC∽△DCB,∴∠DEC=∠DCB=45°,
∵AE⊥BD,∴∠AED=90°,
∴∠AEC=∠AED+∠DEC=90°+45°=135°.
10.证明 (1)连接OB,如图所示,
∵OB=OC,
∴∠OCB=∠OBC.
∵AC是☉O的直径,
∴∠CBA=90°,
∴∠CAB+∠OCB=90°.
∵∠CBD=∠CAB,
∴∠CBD+∠OBC=90°,
∴∠OBD=90°,
∴PD是☉O的切线.
(2)由(1)知PD是☉O的切线,
又直线PA与☉O相切,∴PO垂直平分AB,
∴∠AMP=∠AMO=90°,
∴∠APM+∠PAM=90°.
∵∠OAP=90°,∴∠PAM+∠OAM=90°,
∴∠APM=∠OAM,∴△OAM∽△APM,
∴,
∴AM2=OM·PM.
11.解析 (1)解法一:作AG∥BC,交BE延长线于G,
∵AG∥BC,∴△AGF∽△DBF,
∵AF=4DF,∴AG=4BD.
∵CD=3BD,∴BC=4BD,∴AG=BC,
∵AG∥BC,∴△AGE∽△CBE,
∴=1.
解法二:作CH∥AD,交BE延长线于H,
∵CH∥AD,∴△BDF∽△BCH,∴.
∵CD=3BD,∴BC=4BD,∴CH=4DF.
∵AF=4DF,∴AF=CH.
∵CH∥AD,∴△AEF∽△CEH,
∴=1.
(2)证明:∵BD2=DF·AD,∴.
∵∠BDF=∠ADB,∴△BDF∽△ADB,
∴∠BAD=∠FBD.
∵AB=AC,∴∠ABD=∠ACB,
∴△ABD∽△BCE,∴,
∴CE·AB=BD·BC.
又∵AB=AC,BC=BD+CD=4BD,
∴CE·AC=BC·BC,
∴BC2=4CE·AC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
