2024人教版数学九年级下学期课时练--期末素养综合测试(一)(含解析)
文档属性
| 名称 | 2024人教版数学九年级下学期课时练--期末素养综合测试(一)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 09:21:05 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2024人教版数学九年级下学期
期末素养综合测试(一)
(满分120分,限时100分钟)
一、选择题(每小题3分,共30分)
1.【中华优秀传统文化】(2023湖南衡阳中考改编)作为中国非物质文化遗产之一的紫砂壶,成型工艺特别,造型式样丰富,陶器色泽古朴典雅,从一个方面鲜明地反映了中华民族造型审美意识.下图是一把做工精湛的紫砂壶“景舟石瓢”,其主视图的大致形状是( )
2.(2022黑龙江大庆让胡路期末)在一张比例尺为1∶100的建筑图纸上,量得某座楼的长是6分米,这座楼实际的长与宽的比是3∶1,则这座楼实际的宽是( )
A.40米 B.20米 C.30米 D.10米
3.【数学文化】(2023四川乐山中考)我国汉代数学家赵爽在注解《周髀算经》时给出“赵爽弦图”,如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形面积为25,小正方形面积为1,则sin θ=( )
A.
C.
4.【跨学科·物理】(2023山西朔州山阴模拟)公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即阻力×阻力臂=动力×动力臂,小伟欲用撬棍撬动一块石头,已知在某一平衡状态下,阻力和阻力臂分别是1 000 N和0.4 m,若动力F1>F2(单位:N),则动力臂l1与l2(单位:m)的数量关系为( )
A.l1l2
C.l1=l2 D.无法确定
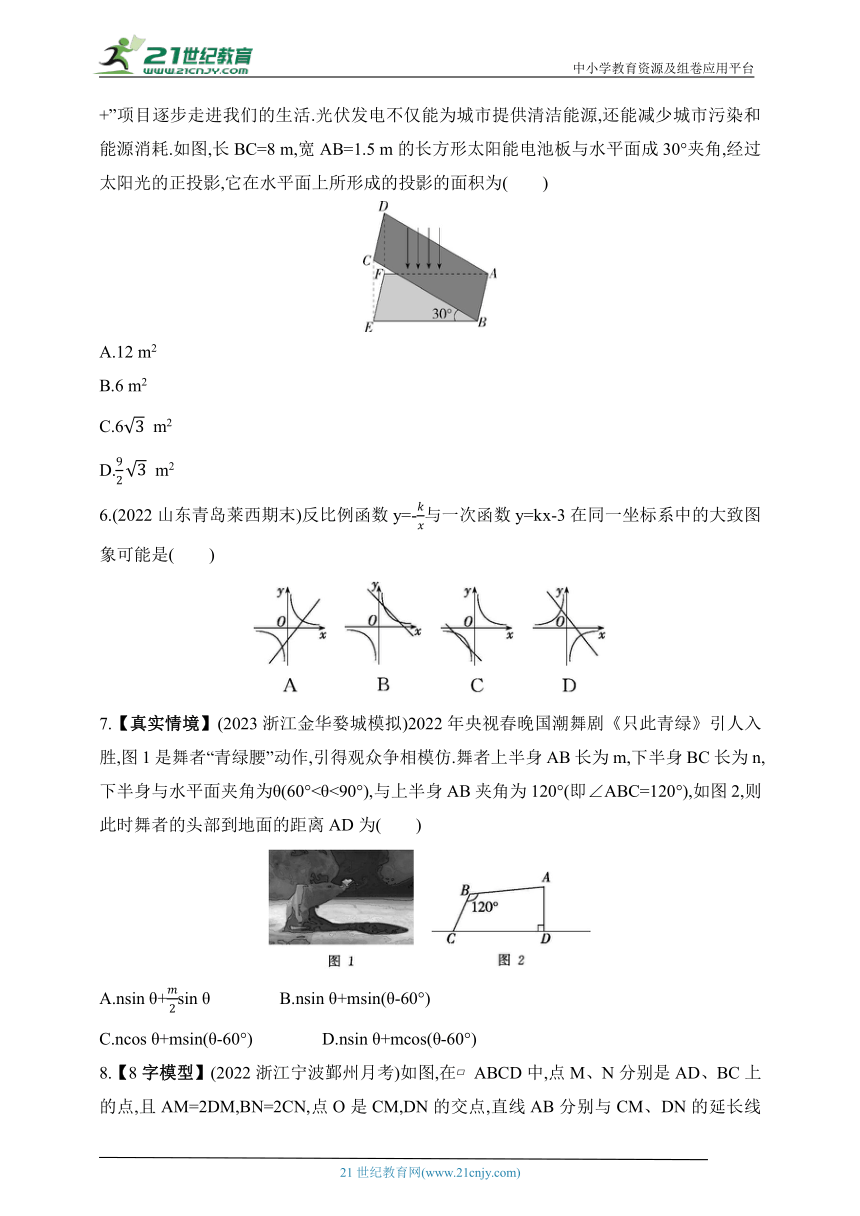
5.【新素材】(2023山东青岛市南期末)随着光伏发电项目投资成本下降,越来越多的“光伏+”项目逐步走进我们的生活.光伏发电不仅能为城市提供清洁能源,还能减少城市污染和能源消耗.如图,长BC=8 m,宽AB=1.5 m的长方形太阳能电池板与水平面成30°夹角,经过太阳光的正投影,它在水平面上所形成的投影的面积为( )
A.12 m2
B.6 m2
C.6 m2
D. m2
6.(2022山东青岛莱西期末)反比例函数y=-与一次函数y=kx-3在同一坐标系中的大致图象可能是( )
7.【真实情境】(2023浙江金华婺城模拟)2022年央视春晚国潮舞剧《只此青绿》引人入胜,图1是舞者“青绿腰”动作,引得观众争相模仿.舞者上半身AB长为m,下半身BC长为n,下半身与水平面夹角为θ(60°<θ<90°),与上半身AB夹角为120°(即∠ABC=120°),如图2,则此时舞者的头部到地面的距离AD为( )
A.nsin θ+sin θ B.nsin θ+msin(θ-60°)
C.ncos θ+msin(θ-60°) D.nsin θ+mcos(θ-60°)
8.【8字模型】(2022浙江宁波鄞州月考)如图,在 ABCD中,点M、N分别是AD、BC上的点,且AM=2DM,BN=2CN,点O是CM,DN的交点,直线AB分别与CM、DN的延长线交于点P、Q.若 ABCD的面积为144,则△POQ的面积为( )
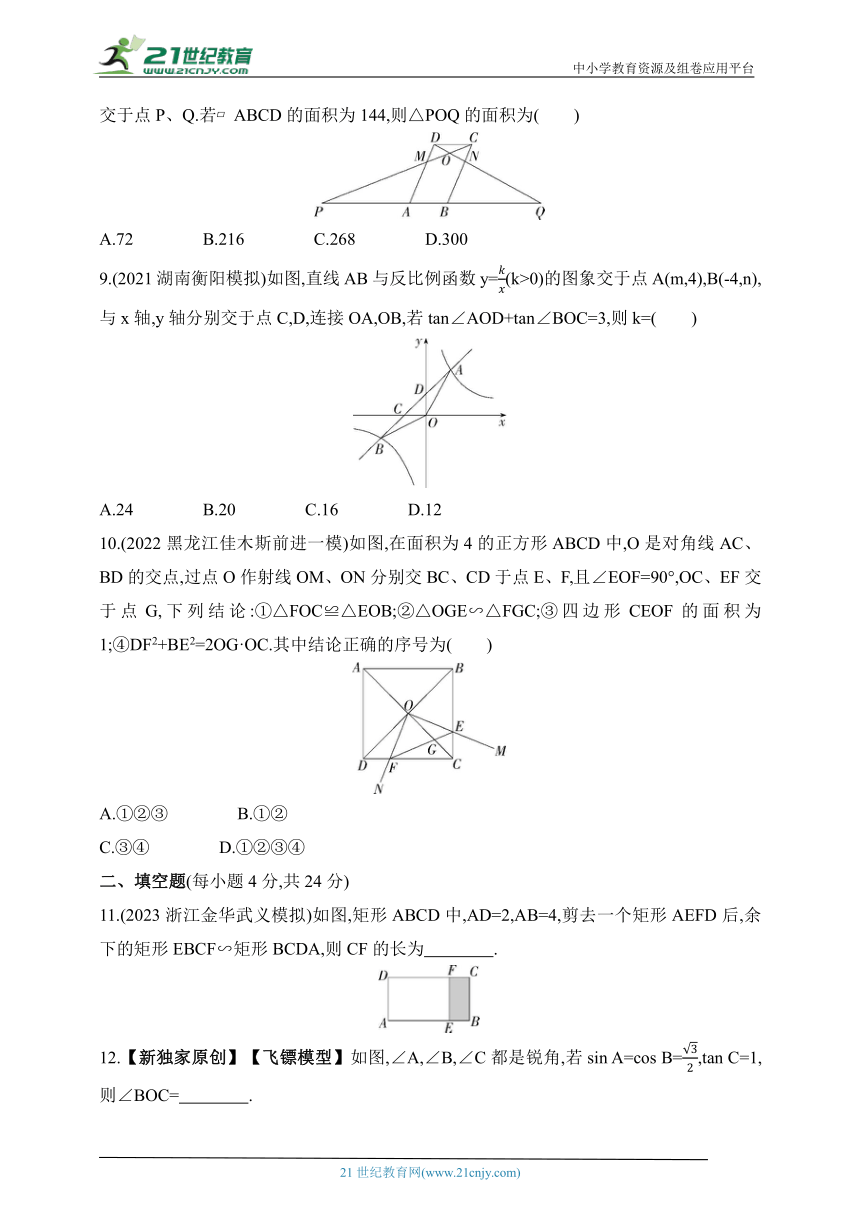
A.72 B.216 C.268 D.300
9.(2021湖南衡阳模拟)如图,直线AB与反比例函数y=(k>0)的图象交于点A(m,4),B(-4,n),与x轴,y轴分别交于点C,D,连接OA,OB,若tan∠AOD+tan∠BOC=3,则k=( )
A.24 B.20 C.16 D.12
10.(2022黑龙江佳木斯前进一模)如图,在面积为4的正方形ABCD中,O是对角线AC、BD的交点,过点O作射线OM、ON分别交BC、CD于点E、F,且∠EOF=90°,OC、EF交于点G,下列结论:①△FOC≌△EOB;②△OGE∽△FGC;③四边形CEOF的面积为1;④DF2+BE2=2OG·OC.其中结论正确的序号为( )
A.①②③ B.①②
C.③④ D.①②③④
二、填空题(每小题4分,共24分)
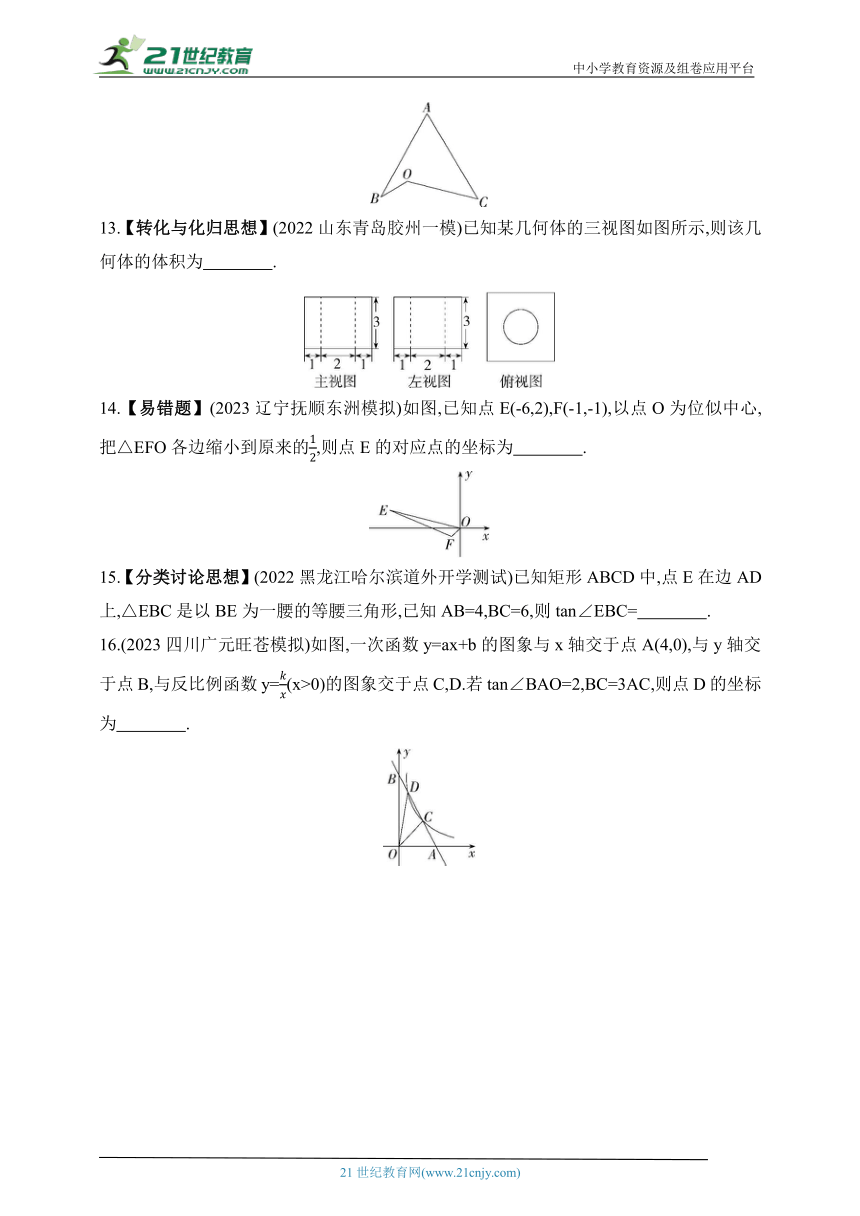
11.(2023浙江金华武义模拟)如图,矩形ABCD中,AD=2,AB=4,剪去一个矩形AEFD后,余下的矩形EBCF∽矩形BCDA,则CF的长为 .
12.【新独家原创】【飞镖模型】如图,∠A,∠B,∠C都是锐角,若sin A=cos B=,tan C=1,则∠BOC= .
13.【转化与化归思想】(2022山东青岛胶州一模)已知某几何体的三视图如图所示,则该几何体的体积为 .
14.【易错题】(2023辽宁抚顺东洲模拟)如图,已知点E(-6,2),F(-1,-1),以点O为位似中心,把△EFO各边缩小到原来的,则点E的对应点的坐标为 .
15.【分类讨论思想】(2022黑龙江哈尔滨道外开学测试)已知矩形ABCD中,点E在边AD上,△EBC是以BE为一腰的等腰三角形,已知AB=4,BC=6,则tan∠EBC= .
16.(2023四川广元旺苍模拟)如图,一次函数y=ax+b的图象与x轴交于点A(4,0),与y轴交于点B,与反比例函数y=(x>0)的图象交于点C,D.若tan∠BAO=2,BC=3AC,则点D的坐标为 .
三、解答题(共66分)
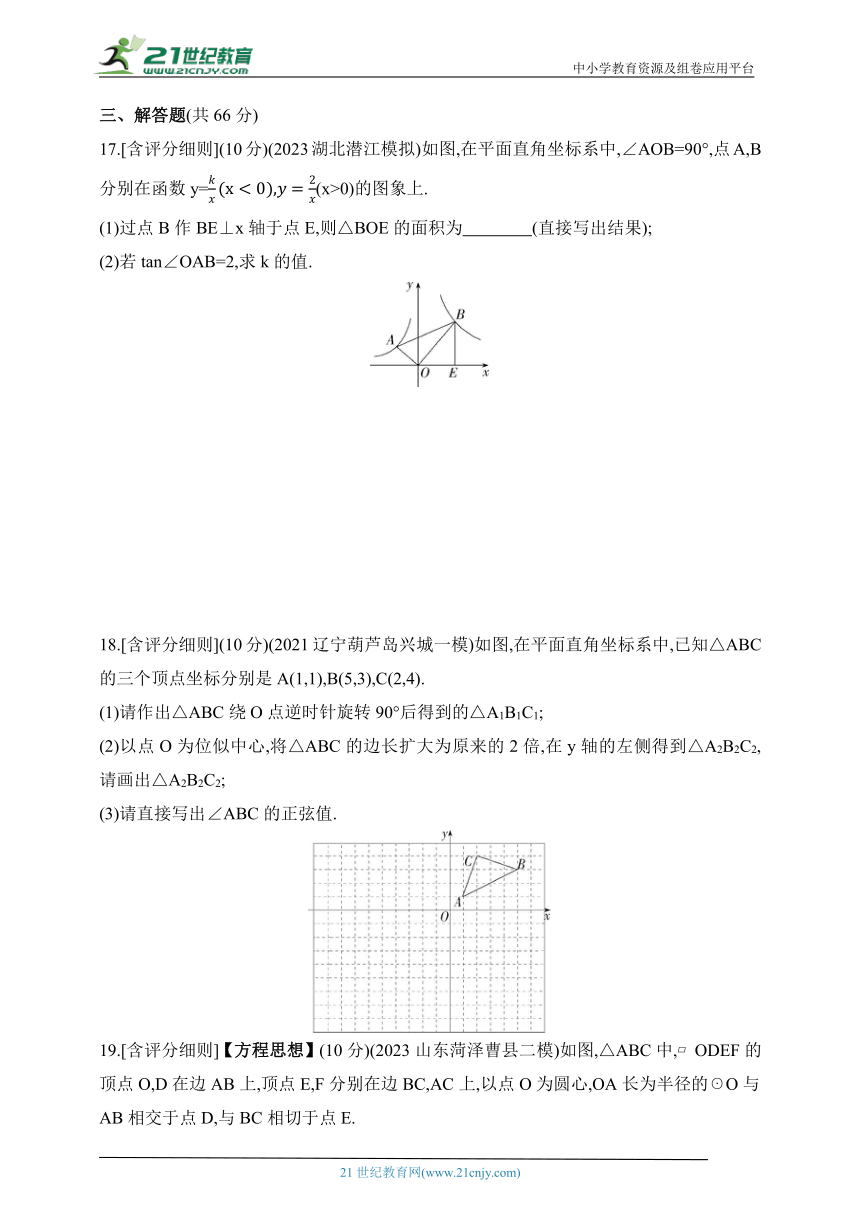
17.[含评分细则](10分)(2023湖北潜江模拟)如图,在平面直角坐标系中,∠AOB=90°,点A,B分别在函数y=(x>0)的图象上.
(1)过点B作BE⊥x轴于点E,则△BOE的面积为 (直接写出结果);
(2)若tan∠OAB=2,求k的值.
18.[含评分细则](10分)(2021辽宁葫芦岛兴城一模)如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(5,3),C(2,4).
(1)请作出△ABC绕O点逆时针旋转90°后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC的边长扩大为原来的2倍,在y轴的左侧得到△A2B2C2,请画出△A2B2C2;
(3)请直接写出∠ABC的正弦值.
19.[含评分细则]【方程思想】(10分)(2023山东菏泽曹县二模)如图,△ABC中, ODEF的顶点O,D在边AB上,顶点E,F分别在边BC,AC上,以点O为圆心,OA长为半径的☉O与AB相交于点D,与BC相切于点E.
(1)求证:△ABC是直角三角形;
(2)若sin∠BAC=,CE=6,求AB的长.
20.[含评分细则](10分)(2022山东聊城中考)聊城市某辖区内的兴国寺有一座宋代仿木楼阁式空心砖塔,塔旁有一棵唐代古槐,称为“宋塔唐槐”.某数学兴趣小组利用无人机测量古槐的高度,如图所示,当无人机从位于塔基B点与古槐底D点之间的地面H点,竖直起飞到正上方45米处的E点时,测得塔AB的顶端A和古槐CD的顶端C的俯角分别为26.6°和76°(点B,H,D三点在同一直线上).已知塔高为39米,塔基B点与树底D点的水平距离为20米,求古槐的高度(结果精确到1米).(参考数据:sin 26.6°≈0.45,cos 26.6°≈0.89,tan 26.6°≈0.50,sin 76°≈0.97,cos 76°≈0.24,tan 76°≈4.01)
21.[含评分细则](12分)(2022河南商丘二模)某医药研究所研制了一种具有缓释功能的新药,在试验药效时发现:成人按规定剂量服用后,药物从第0.5小时开始起效,第2小时达到最高血药浓度,为12微克/毫升,并维持这一最高值直至第4小时结束,接着开始衰退,血液中每毫升含药量y(微克)与时间x(小时)的函数关系如图,并发现衰退时y与x成反比例函数关系.
(1)①当0.5≤x≤2时,y与x之间的函数表达式为 ;
②当x>4时,y与x之间的函数表达式为 .
(2)如果每毫升血液中含药量不低于4微克时有效,求一次服药后的有效时间是多少小时.
22.[含评分细则]【手拉手模型】(14分)(2022山东烟台中考)【问题呈现】如图1,△ABC 和△ADE都是等边三角形,连接BD,CE.求证:BD=CE.
【类比探究】如图2,△ABC 和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°.连接BD,CE.请直接写出的值.
【拓展提升】如图3,△ABC 和△ADE都是直角三角形,∠ABC=∠ADE=90°,且.连接BD,CE.
(1)求的值;
(2)延长CE交BD于点F,交AB于点G.求sin∠BFC的值.
答案全解全析
1.D 从前往后看,所看到的视图是选项D中图形.故选D.
2.B 设这座楼实际的长是x分米,根据题意得1∶100=6∶x,解得x=600,600分米=60米,设这座楼实际的宽是y米,根据题意得3∶1=60∶y,解得y=20.故选B.
3.A 设大正方形的边长为c,直角三角形的短直角边长为a,长直角边长为b,由题意,得c2=25,b-a==1,a2+b2=c2,∴a=3,b=4,c=5,∴sin θ=.故选A.
4.A ∵阻力×阻力臂=动力×动力臂,∴动力F(单位:N)与动力臂l(单位:m)的函数解析式为1 000×0.4=Fl,则l=(F>0),∴动力臂l是动力F的反比例函数,且动力臂l随动力F的增大而减小,∵动力F1>F2,∴动力臂l15.C 在Rt△BCE中,∵∠CBE=30°,BC=8 m,∴BE=BC·cos 30°=8×(m),∵AB=1.5 m,∴太阳能电池板在水平面上所形成的投影的面积=1.5×4 m2.故选C.
6.C 当k>0时,一次函数y=kx-3的图象经过第一、三、四象限,反比例函数y=-的图象位于第二、四象限,无符合选项;当k<0时,一次函数y=kx-3的图象经过第二、三、四象限,反比例函数y=-的图象位于第一、三象限,选项C符合.故选C.
7.B 如图,过点B作BE⊥CD于点E,作BF⊥AD于点F.∵∠BED=∠EDF=∠BFD=90°,∴四边形BEDF为矩形,∴BE=DF,∠EBF=90°,∵∠BCE=θ,∴∠CBE=90°-θ,∵∠ABC=120°,∴∠ABF=120°-90°-(90°-θ)=θ-60°,在Rt△BCE中,BE=BC×sin∠BCE=nsin θ,∴DF=BE=nsin θ,在Rt△ABF中,AF=AB×sin∠ABF=msin(θ-60°),∴AD=DF+AF=nsin θ+msin(θ-60°).故选B.
8.D 如图,连接MN,∵四边形ABCD是平行四边形,∴CD∥AB,AD∥BC,AD=BC.∵AM=2DM,BN=2CN,∴DM=BC,∴DM=CN,∴四边形CDMN是平行四边形,AM=BN.∵AM∥BN,∴四边形AMNB是平行四边形.设S△OMN=x,则S四边形CDMN=4x,∴S四边形ABNM=8x.∵ ABCD的面积为144,∴4x+8x=144,∴x=12,∴S△MCD=2x=24,∵CD∥PA,∴△CDM∽△PAM,∴,∴S△PAM=24×4=96,同理,S△BQN=96,∵S四边形ABNM=8x=96,∴△POQ的面积=S△OMN+S△PAM+S△BQN+S四边形ABNM=12+96+96+96=300.故选D.
9.A 如图,过点A作AE⊥y轴于E,过点B作BF⊥x轴于F.在Rt△AOE中,tan∠AOE=,在Rt△BOF中,tan∠BOF=,又tan∠AOD+tan∠BOC=3,所以=3①,∵A(m,4),B(-4,n)都在反比例函数y=(k>0)的图象上,∴4m=-4n,∴m+n=0②,联立①②,解得m=6,n=-6,则A(6,4),B(-4,-6),将点A的坐标代入反比例函数表达式得k=4×6=24,
故选A.
10.D ①∵四边形ABCD是正方形,∴OC=OB,AC⊥BD,∠OCF=∠OBE=45°.∵∠MON=90°=∠BOC,∴∠BOE=∠COF,∴△BOE≌△COF(ASA),故①正确;
②∵∠EOF=∠ECF=90°,∴O,E,C,F四点共圆,∴∠EOG=∠CFG,∠OEG=∠FCG,∴△OGE∽△FGC,故②正确;
③∵△BOE≌△COF,∴S△BOE=S△COF,∴S四边形CEOF=S△BOC==1,故③正确;
④∵∠OEG=∠FCG=45°=∠OCE,∠EOG=∠COE,
∴△OEG∽△OCE,∴,∴OG·OC=OE2,∵OC=EF,∴OG·AC=EF2,∵△BOE≌△COF,∴BE=CF,∴CE=DF,在Rt△CEF中,CF2+CE2=EF2,∴BE2+DF2=EF2,∴OG·AC=BE2+DF2,∴DF2+BE2=2OG·OC,故④正确.
故选D.
11.1
解析 ∵四边形ABCD是矩形,∴AD=BC=2,AB=DC=4,∵矩形EBCF∽矩形BCDA,∴,即,∴CF=1.
12.135°
解析 ∵∠A,∠B,∠C都是锐角,sin A=cos B=,tan C=1,∴∠A=60°,∠B=30°,∠C=45°.如图,延长BO交AC于D,则∠CDO=∠A+∠B=60°+30°=90°,∴∠BOC=∠CDO+∠C=90°+45°=135°.
13.48-3π
解析 由三视图知,该几何体是由长为4、宽为4、高为3的长方体中间去掉底面直径为2,高为3的圆柱体形成的,∴该几何体的体积为4×4×3-π·12×3=48-3π.
14.(-3,1)或(3,-1)
解析 ∵以点O为位似中心,把△EFO各边缩小到原来的,点E的坐标为(-6,2),∴点E的对应点的坐标为,即(-3,1)或(3,-1).
易错点 易忽略其中一种情况.
15.
解析 根据题意,当BE=CE时(如图1),过点E作EM⊥BC于点M,得BM=CM.∵AB=4,BC=6,∴EM=4,BM=BC=3,∴tan∠EBC=;当BE=BC时(如图2),过点E作EN⊥BC于点N,得BE=BC=6,EN=AB=4,∴BN=,∴tan∠EBC=.
16.(1,6)
解析 在Rt△AOB中,∵tan∠BAO=2,∴BO=2OA.∵A(4,0),∴B(0,8).A、B两点在函数y=ax+b的图象上,将A(4,0)、B(0,8)代入y=ax+b得:∴一次函数的解析式为y=-2x+8.设C(x1,y1),如图,过点C作CE⊥x轴,垂足为E,则CE∥BO,∴△ACE∽△ABO,∴,又∵BC=3AC,∴,即,则CE=2,即y1=2,∴-2x1+8=2,∴x1=3,∴C(3,2),∴k=x1y1=3×2=6,∴反比例函数的解析式为y=.联立∴D(1,6).
17.解析 (1)1.3分
详解:∵点B在y=(x>0)的图象上,且BE⊥x轴,
∴S△BOE==1.
(2)如图,过点A作AF⊥x轴于点F,
则有∠AFO=90°,∴∠FAO+∠AOF=90°,
∵∠AOB=90°,∴∠AOF+∠BOE=90°.4分
∴∠FAO=∠BOE,
∴△AOF∽△OBE,6分
∴=(tan∠OAB)2=4,
∴S△AOF=S△BOE=,8分
∴,又k<0,
∴k=-.10分
18.解析 (1)如图,△A1B1C1即为所作.3分
(2)如图,△A2B2C2即为所作.6分
(3)sin∠ABC=.10分
详解:∵BC=,∴BC2+AC2=AB2,∴△ABC为等腰直角三角形,∴sin∠ABC=sin 45°=.
19.解析 (1)证明:连接OE,
∵☉O与BC相切于点E,∴OE⊥BC.1分
∵四边形ODEF为平行四边形,
∴OD∥EF,OD=EF.2分
∵OA=OD,∴OA=EF,
∴四边形AOEF是平行四边形,3分
∴AC∥OE,∴∠C=∠OEB=90°,
∴△ABC是直角三角形.4分
(2)∵EF∥AB,∴∠CFE=∠BAC,5分
∴sin∠CFE=sin∠BAC=,
∴EF==10,6分
∴CF==8.7分
由(1)知四边形AOEF是平行四边形,又∵OA=OE,∴四边形AOEF是菱形,
∴AF=EF=10,∴AC=AF+CF=18.8分
设BC=3x,则AB=5x,
∴(5x)2=(3x)2+182,∴x=(舍去负值),
∴AB=5×.10分
20.解析 如图,过点A作AM⊥EH于M,过点C作CN⊥EH于N,
由题意知,AM=BH,CN=DH,AB=MH,2分
在Rt△AME中,∠EAM=26.6°,
∵tan∠EAM=,
∴AM==12米,4分
∴BH=AM=12米,
∵BD=20米,∴DH=BD-BH=8米,
∴CN=8米,7分
在Rt△ENC中,∠ECN=76°,
∵tan∠ECN=,
∴EN=CN·tan∠ECN≈8×4.01=32.08米,9分
∴CD=NH=EH-EN=12.92≈13米,
即古槐的高度约为13米.10分
21.解析 (1)①y=8x-4.4分
详解:当0.5≤x≤2时,设y=kx+b,
由图象可知y=kx+b的图象过点(0.5,0)和(2,12),
∴
∴当0.5≤x≤2时,y与x之间的函数表达式为y=8x-4.
②y=.7分
详解:当x≥4时,y与x成反比例函数关系,
设y=,把(4,12)代入得12=,解得m=48,
∴当x>4时,y与x之间的函数表达式为y=.
(2)把y=4代入y=8x-4,得4=8x-4,解得x=1,8分
把y=4代入y=,得x=12,10分
∴有效时间为12-1=11(小时).
答:一次服药后的有效时间是11小时.12分
22.解析 【问题呈现】证明:∵△ABC和△ADE都是等边三角形,
∴AD=AE,AB=AC,∠DAE=∠BAC=60°,2分
∴∠DAE-∠BAE=∠BAC-∠BAE,
∴∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),∴BD=CE.4分
【类比探究】.8分
详解:∵△ABC和△ADE都是等腰直角三角形,
∴,∠DAE=∠BAC=45°,
∴∠DAE-∠BAE=∠BAC-∠BAE,
∴∠BAD=∠CAE,∴△BAD∽△CAE,
∴.
【拓展提升】(1)∵,∠ABC=∠ADE=90°,
∴△ABC∽△ADE,∴∠BAC=∠DAE,,
∴∠CAE=∠BAD,∴△CAE∽△BAD,
∴.10分
由,设AB=3t,BC=4t,
则由勾股定理得AC=5t,∴,
∴.12分
(2)由(1)得:△CAE∽△BAD,∴∠ACE=∠ABD,
又∵∠AGC=∠BGF,∴∠BFC=∠BAC,
∴sin∠BFC=sin∠BAC=.14分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版数学九年级下学期
期末素养综合测试(一)
(满分120分,限时100分钟)
一、选择题(每小题3分,共30分)
1.【中华优秀传统文化】(2023湖南衡阳中考改编)作为中国非物质文化遗产之一的紫砂壶,成型工艺特别,造型式样丰富,陶器色泽古朴典雅,从一个方面鲜明地反映了中华民族造型审美意识.下图是一把做工精湛的紫砂壶“景舟石瓢”,其主视图的大致形状是( )
2.(2022黑龙江大庆让胡路期末)在一张比例尺为1∶100的建筑图纸上,量得某座楼的长是6分米,这座楼实际的长与宽的比是3∶1,则这座楼实际的宽是( )
A.40米 B.20米 C.30米 D.10米
3.【数学文化】(2023四川乐山中考)我国汉代数学家赵爽在注解《周髀算经》时给出“赵爽弦图”,如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形面积为25,小正方形面积为1,则sin θ=( )
A.
C.
4.【跨学科·物理】(2023山西朔州山阴模拟)公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即阻力×阻力臂=动力×动力臂,小伟欲用撬棍撬动一块石头,已知在某一平衡状态下,阻力和阻力臂分别是1 000 N和0.4 m,若动力F1>F2(单位:N),则动力臂l1与l2(单位:m)的数量关系为( )
A.l1
C.l1=l2 D.无法确定
5.【新素材】(2023山东青岛市南期末)随着光伏发电项目投资成本下降,越来越多的“光伏+”项目逐步走进我们的生活.光伏发电不仅能为城市提供清洁能源,还能减少城市污染和能源消耗.如图,长BC=8 m,宽AB=1.5 m的长方形太阳能电池板与水平面成30°夹角,经过太阳光的正投影,它在水平面上所形成的投影的面积为( )
A.12 m2
B.6 m2
C.6 m2
D. m2
6.(2022山东青岛莱西期末)反比例函数y=-与一次函数y=kx-3在同一坐标系中的大致图象可能是( )
7.【真实情境】(2023浙江金华婺城模拟)2022年央视春晚国潮舞剧《只此青绿》引人入胜,图1是舞者“青绿腰”动作,引得观众争相模仿.舞者上半身AB长为m,下半身BC长为n,下半身与水平面夹角为θ(60°<θ<90°),与上半身AB夹角为120°(即∠ABC=120°),如图2,则此时舞者的头部到地面的距离AD为( )
A.nsin θ+sin θ B.nsin θ+msin(θ-60°)
C.ncos θ+msin(θ-60°) D.nsin θ+mcos(θ-60°)
8.【8字模型】(2022浙江宁波鄞州月考)如图,在 ABCD中,点M、N分别是AD、BC上的点,且AM=2DM,BN=2CN,点O是CM,DN的交点,直线AB分别与CM、DN的延长线交于点P、Q.若 ABCD的面积为144,则△POQ的面积为( )
A.72 B.216 C.268 D.300
9.(2021湖南衡阳模拟)如图,直线AB与反比例函数y=(k>0)的图象交于点A(m,4),B(-4,n),与x轴,y轴分别交于点C,D,连接OA,OB,若tan∠AOD+tan∠BOC=3,则k=( )
A.24 B.20 C.16 D.12
10.(2022黑龙江佳木斯前进一模)如图,在面积为4的正方形ABCD中,O是对角线AC、BD的交点,过点O作射线OM、ON分别交BC、CD于点E、F,且∠EOF=90°,OC、EF交于点G,下列结论:①△FOC≌△EOB;②△OGE∽△FGC;③四边形CEOF的面积为1;④DF2+BE2=2OG·OC.其中结论正确的序号为( )
A.①②③ B.①②
C.③④ D.①②③④
二、填空题(每小题4分,共24分)
11.(2023浙江金华武义模拟)如图,矩形ABCD中,AD=2,AB=4,剪去一个矩形AEFD后,余下的矩形EBCF∽矩形BCDA,则CF的长为 .
12.【新独家原创】【飞镖模型】如图,∠A,∠B,∠C都是锐角,若sin A=cos B=,tan C=1,则∠BOC= .
13.【转化与化归思想】(2022山东青岛胶州一模)已知某几何体的三视图如图所示,则该几何体的体积为 .
14.【易错题】(2023辽宁抚顺东洲模拟)如图,已知点E(-6,2),F(-1,-1),以点O为位似中心,把△EFO各边缩小到原来的,则点E的对应点的坐标为 .
15.【分类讨论思想】(2022黑龙江哈尔滨道外开学测试)已知矩形ABCD中,点E在边AD上,△EBC是以BE为一腰的等腰三角形,已知AB=4,BC=6,则tan∠EBC= .
16.(2023四川广元旺苍模拟)如图,一次函数y=ax+b的图象与x轴交于点A(4,0),与y轴交于点B,与反比例函数y=(x>0)的图象交于点C,D.若tan∠BAO=2,BC=3AC,则点D的坐标为 .
三、解答题(共66分)
17.[含评分细则](10分)(2023湖北潜江模拟)如图,在平面直角坐标系中,∠AOB=90°,点A,B分别在函数y=(x>0)的图象上.
(1)过点B作BE⊥x轴于点E,则△BOE的面积为 (直接写出结果);
(2)若tan∠OAB=2,求k的值.
18.[含评分细则](10分)(2021辽宁葫芦岛兴城一模)如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(5,3),C(2,4).
(1)请作出△ABC绕O点逆时针旋转90°后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC的边长扩大为原来的2倍,在y轴的左侧得到△A2B2C2,请画出△A2B2C2;
(3)请直接写出∠ABC的正弦值.
19.[含评分细则]【方程思想】(10分)(2023山东菏泽曹县二模)如图,△ABC中, ODEF的顶点O,D在边AB上,顶点E,F分别在边BC,AC上,以点O为圆心,OA长为半径的☉O与AB相交于点D,与BC相切于点E.
(1)求证:△ABC是直角三角形;
(2)若sin∠BAC=,CE=6,求AB的长.
20.[含评分细则](10分)(2022山东聊城中考)聊城市某辖区内的兴国寺有一座宋代仿木楼阁式空心砖塔,塔旁有一棵唐代古槐,称为“宋塔唐槐”.某数学兴趣小组利用无人机测量古槐的高度,如图所示,当无人机从位于塔基B点与古槐底D点之间的地面H点,竖直起飞到正上方45米处的E点时,测得塔AB的顶端A和古槐CD的顶端C的俯角分别为26.6°和76°(点B,H,D三点在同一直线上).已知塔高为39米,塔基B点与树底D点的水平距离为20米,求古槐的高度(结果精确到1米).(参考数据:sin 26.6°≈0.45,cos 26.6°≈0.89,tan 26.6°≈0.50,sin 76°≈0.97,cos 76°≈0.24,tan 76°≈4.01)
21.[含评分细则](12分)(2022河南商丘二模)某医药研究所研制了一种具有缓释功能的新药,在试验药效时发现:成人按规定剂量服用后,药物从第0.5小时开始起效,第2小时达到最高血药浓度,为12微克/毫升,并维持这一最高值直至第4小时结束,接着开始衰退,血液中每毫升含药量y(微克)与时间x(小时)的函数关系如图,并发现衰退时y与x成反比例函数关系.
(1)①当0.5≤x≤2时,y与x之间的函数表达式为 ;
②当x>4时,y与x之间的函数表达式为 .
(2)如果每毫升血液中含药量不低于4微克时有效,求一次服药后的有效时间是多少小时.
22.[含评分细则]【手拉手模型】(14分)(2022山东烟台中考)【问题呈现】如图1,△ABC 和△ADE都是等边三角形,连接BD,CE.求证:BD=CE.
【类比探究】如图2,△ABC 和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°.连接BD,CE.请直接写出的值.
【拓展提升】如图3,△ABC 和△ADE都是直角三角形,∠ABC=∠ADE=90°,且.连接BD,CE.
(1)求的值;
(2)延长CE交BD于点F,交AB于点G.求sin∠BFC的值.
答案全解全析
1.D 从前往后看,所看到的视图是选项D中图形.故选D.
2.B 设这座楼实际的长是x分米,根据题意得1∶100=6∶x,解得x=600,600分米=60米,设这座楼实际的宽是y米,根据题意得3∶1=60∶y,解得y=20.故选B.
3.A 设大正方形的边长为c,直角三角形的短直角边长为a,长直角边长为b,由题意,得c2=25,b-a==1,a2+b2=c2,∴a=3,b=4,c=5,∴sin θ=.故选A.
4.A ∵阻力×阻力臂=动力×动力臂,∴动力F(单位:N)与动力臂l(单位:m)的函数解析式为1 000×0.4=Fl,则l=(F>0),∴动力臂l是动力F的反比例函数,且动力臂l随动力F的增大而减小,∵动力F1>F2,∴动力臂l1
6.C 当k>0时,一次函数y=kx-3的图象经过第一、三、四象限,反比例函数y=-的图象位于第二、四象限,无符合选项;当k<0时,一次函数y=kx-3的图象经过第二、三、四象限,反比例函数y=-的图象位于第一、三象限,选项C符合.故选C.
7.B 如图,过点B作BE⊥CD于点E,作BF⊥AD于点F.∵∠BED=∠EDF=∠BFD=90°,∴四边形BEDF为矩形,∴BE=DF,∠EBF=90°,∵∠BCE=θ,∴∠CBE=90°-θ,∵∠ABC=120°,∴∠ABF=120°-90°-(90°-θ)=θ-60°,在Rt△BCE中,BE=BC×sin∠BCE=nsin θ,∴DF=BE=nsin θ,在Rt△ABF中,AF=AB×sin∠ABF=msin(θ-60°),∴AD=DF+AF=nsin θ+msin(θ-60°).故选B.
8.D 如图,连接MN,∵四边形ABCD是平行四边形,∴CD∥AB,AD∥BC,AD=BC.∵AM=2DM,BN=2CN,∴DM=BC,∴DM=CN,∴四边形CDMN是平行四边形,AM=BN.∵AM∥BN,∴四边形AMNB是平行四边形.设S△OMN=x,则S四边形CDMN=4x,∴S四边形ABNM=8x.∵ ABCD的面积为144,∴4x+8x=144,∴x=12,∴S△MCD=2x=24,∵CD∥PA,∴△CDM∽△PAM,∴,∴S△PAM=24×4=96,同理,S△BQN=96,∵S四边形ABNM=8x=96,∴△POQ的面积=S△OMN+S△PAM+S△BQN+S四边形ABNM=12+96+96+96=300.故选D.
9.A 如图,过点A作AE⊥y轴于E,过点B作BF⊥x轴于F.在Rt△AOE中,tan∠AOE=,在Rt△BOF中,tan∠BOF=,又tan∠AOD+tan∠BOC=3,所以=3①,∵A(m,4),B(-4,n)都在反比例函数y=(k>0)的图象上,∴4m=-4n,∴m+n=0②,联立①②,解得m=6,n=-6,则A(6,4),B(-4,-6),将点A的坐标代入反比例函数表达式得k=4×6=24,
故选A.
10.D ①∵四边形ABCD是正方形,∴OC=OB,AC⊥BD,∠OCF=∠OBE=45°.∵∠MON=90°=∠BOC,∴∠BOE=∠COF,∴△BOE≌△COF(ASA),故①正确;
②∵∠EOF=∠ECF=90°,∴O,E,C,F四点共圆,∴∠EOG=∠CFG,∠OEG=∠FCG,∴△OGE∽△FGC,故②正确;
③∵△BOE≌△COF,∴S△BOE=S△COF,∴S四边形CEOF=S△BOC==1,故③正确;
④∵∠OEG=∠FCG=45°=∠OCE,∠EOG=∠COE,
∴△OEG∽△OCE,∴,∴OG·OC=OE2,∵OC=EF,∴OG·AC=EF2,∵△BOE≌△COF,∴BE=CF,∴CE=DF,在Rt△CEF中,CF2+CE2=EF2,∴BE2+DF2=EF2,∴OG·AC=BE2+DF2,∴DF2+BE2=2OG·OC,故④正确.
故选D.
11.1
解析 ∵四边形ABCD是矩形,∴AD=BC=2,AB=DC=4,∵矩形EBCF∽矩形BCDA,∴,即,∴CF=1.
12.135°
解析 ∵∠A,∠B,∠C都是锐角,sin A=cos B=,tan C=1,∴∠A=60°,∠B=30°,∠C=45°.如图,延长BO交AC于D,则∠CDO=∠A+∠B=60°+30°=90°,∴∠BOC=∠CDO+∠C=90°+45°=135°.
13.48-3π
解析 由三视图知,该几何体是由长为4、宽为4、高为3的长方体中间去掉底面直径为2,高为3的圆柱体形成的,∴该几何体的体积为4×4×3-π·12×3=48-3π.
14.(-3,1)或(3,-1)
解析 ∵以点O为位似中心,把△EFO各边缩小到原来的,点E的坐标为(-6,2),∴点E的对应点的坐标为,即(-3,1)或(3,-1).
易错点 易忽略其中一种情况.
15.
解析 根据题意,当BE=CE时(如图1),过点E作EM⊥BC于点M,得BM=CM.∵AB=4,BC=6,∴EM=4,BM=BC=3,∴tan∠EBC=;当BE=BC时(如图2),过点E作EN⊥BC于点N,得BE=BC=6,EN=AB=4,∴BN=,∴tan∠EBC=.
16.(1,6)
解析 在Rt△AOB中,∵tan∠BAO=2,∴BO=2OA.∵A(4,0),∴B(0,8).A、B两点在函数y=ax+b的图象上,将A(4,0)、B(0,8)代入y=ax+b得:∴一次函数的解析式为y=-2x+8.设C(x1,y1),如图,过点C作CE⊥x轴,垂足为E,则CE∥BO,∴△ACE∽△ABO,∴,又∵BC=3AC,∴,即,则CE=2,即y1=2,∴-2x1+8=2,∴x1=3,∴C(3,2),∴k=x1y1=3×2=6,∴反比例函数的解析式为y=.联立∴D(1,6).
17.解析 (1)1.3分
详解:∵点B在y=(x>0)的图象上,且BE⊥x轴,
∴S△BOE==1.
(2)如图,过点A作AF⊥x轴于点F,
则有∠AFO=90°,∴∠FAO+∠AOF=90°,
∵∠AOB=90°,∴∠AOF+∠BOE=90°.4分
∴∠FAO=∠BOE,
∴△AOF∽△OBE,6分
∴=(tan∠OAB)2=4,
∴S△AOF=S△BOE=,8分
∴,又k<0,
∴k=-.10分
18.解析 (1)如图,△A1B1C1即为所作.3分
(2)如图,△A2B2C2即为所作.6分
(3)sin∠ABC=.10分
详解:∵BC=,∴BC2+AC2=AB2,∴△ABC为等腰直角三角形,∴sin∠ABC=sin 45°=.
19.解析 (1)证明:连接OE,
∵☉O与BC相切于点E,∴OE⊥BC.1分
∵四边形ODEF为平行四边形,
∴OD∥EF,OD=EF.2分
∵OA=OD,∴OA=EF,
∴四边形AOEF是平行四边形,3分
∴AC∥OE,∴∠C=∠OEB=90°,
∴△ABC是直角三角形.4分
(2)∵EF∥AB,∴∠CFE=∠BAC,5分
∴sin∠CFE=sin∠BAC=,
∴EF==10,6分
∴CF==8.7分
由(1)知四边形AOEF是平行四边形,又∵OA=OE,∴四边形AOEF是菱形,
∴AF=EF=10,∴AC=AF+CF=18.8分
设BC=3x,则AB=5x,
∴(5x)2=(3x)2+182,∴x=(舍去负值),
∴AB=5×.10分
20.解析 如图,过点A作AM⊥EH于M,过点C作CN⊥EH于N,
由题意知,AM=BH,CN=DH,AB=MH,2分
在Rt△AME中,∠EAM=26.6°,
∵tan∠EAM=,
∴AM==12米,4分
∴BH=AM=12米,
∵BD=20米,∴DH=BD-BH=8米,
∴CN=8米,7分
在Rt△ENC中,∠ECN=76°,
∵tan∠ECN=,
∴EN=CN·tan∠ECN≈8×4.01=32.08米,9分
∴CD=NH=EH-EN=12.92≈13米,
即古槐的高度约为13米.10分
21.解析 (1)①y=8x-4.4分
详解:当0.5≤x≤2时,设y=kx+b,
由图象可知y=kx+b的图象过点(0.5,0)和(2,12),
∴
∴当0.5≤x≤2时,y与x之间的函数表达式为y=8x-4.
②y=.7分
详解:当x≥4时,y与x成反比例函数关系,
设y=,把(4,12)代入得12=,解得m=48,
∴当x>4时,y与x之间的函数表达式为y=.
(2)把y=4代入y=8x-4,得4=8x-4,解得x=1,8分
把y=4代入y=,得x=12,10分
∴有效时间为12-1=11(小时).
答:一次服药后的有效时间是11小时.12分
22.解析 【问题呈现】证明:∵△ABC和△ADE都是等边三角形,
∴AD=AE,AB=AC,∠DAE=∠BAC=60°,2分
∴∠DAE-∠BAE=∠BAC-∠BAE,
∴∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),∴BD=CE.4分
【类比探究】.8分
详解:∵△ABC和△ADE都是等腰直角三角形,
∴,∠DAE=∠BAC=45°,
∴∠DAE-∠BAE=∠BAC-∠BAE,
∴∠BAD=∠CAE,∴△BAD∽△CAE,
∴.
【拓展提升】(1)∵,∠ABC=∠ADE=90°,
∴△ABC∽△ADE,∴∠BAC=∠DAE,,
∴∠CAE=∠BAD,∴△CAE∽△BAD,
∴.10分
由,设AB=3t,BC=4t,
则由勾股定理得AC=5t,∴,
∴.12分
(2)由(1)得:△CAE∽△BAD,∴∠ACE=∠ABD,
又∵∠AGC=∠BGF,∴∠BFC=∠BAC,
∴sin∠BFC=sin∠BAC=.14分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
