用配方法解一元二次方程
图片预览

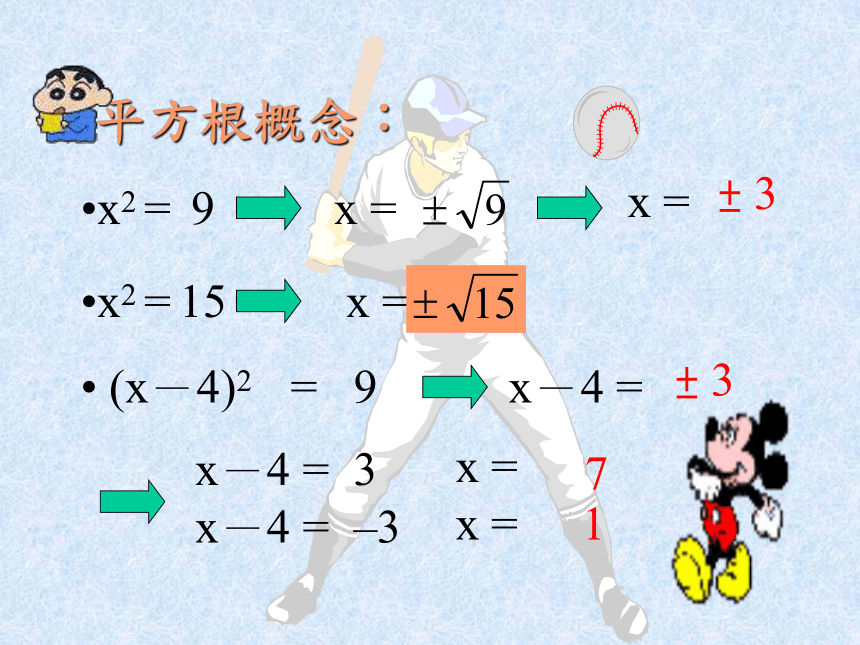


文档简介
课件17张PPT。配方法解一元二次方程式第三冊§3-3平方根概念:x2 = 9 x = x =x2 = 15 x = (x-4)2 = 9 x-4 =± 3x-4 = 3
x-4 = –3 x =
x = 7
± 31背出公式:(a ± b)2
x2 + 2.x.3 + 32 =
(x+3)2
觀 察:=(x+3)2
32a2±2ab+b2 =
計 算:
x2 + 6x+
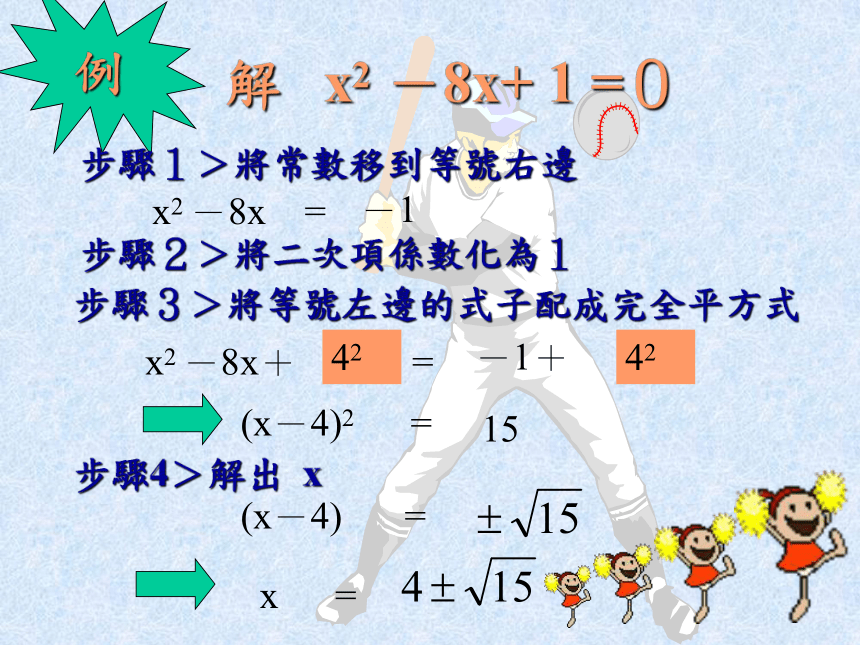
配成完全平方:解 x2 -8x+ 1 =0步驟1>將常數移到等號右邊 (x-4)2 =-1例
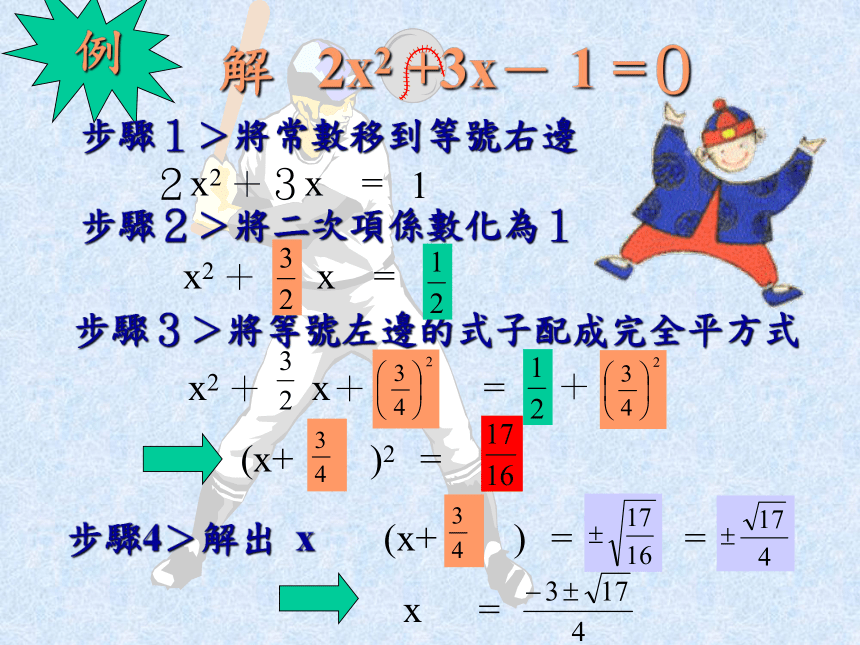
x2 -8x =步驟2>將二次項係數化為1步驟3>將等號左邊的式子配成完全平方式x2 -8x+ =42-1+4215步驟4>解出 x (x-4) = x =解 2x2 +3x- 1 =0步驟1>將常數移到等號右邊 (x+ )2 =1例
2x2 +3x =步驟2>將二次項係數化為1步驟3>將等號左邊的式子配成完全平方式步驟4>解出 x x = x2 + x =x2 + x+ =+ = (x+ ) =練習作業一:求下列方程式之解:
1>X2=49
2> X2-9 =0
3> 5 X2 = 5
4> 4X2 -13 = 12
5>(X -2)2 = 25
6>(3X+2)2 = 2
7>(3X+2)2-49 = 0
8>31(2X-5)2 = 0
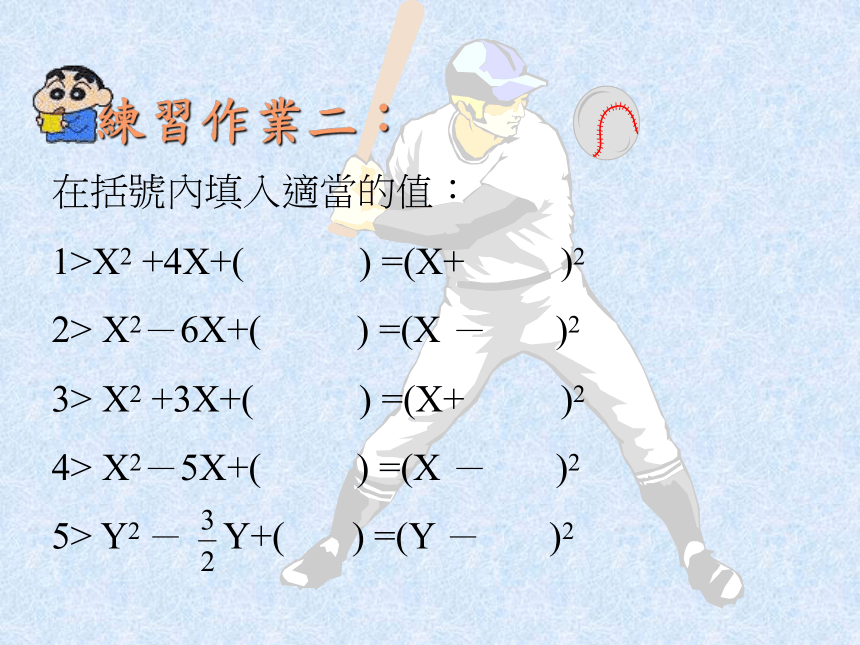
練習作業二:在括號內填入適當的值:
1>X2 +4X+( ) =(X+ )2
2> X2-6X+( ) =(X - )2
3> X2 +3X+( ) =(X+ )2
4> X2-5X+( ) =(X - )2
5> Y2 - Y+( ) =(Y - )2 練習作業三:用配方法求下列方程式之解:
1>X2+2x-399=0
2> X2-6x+2=0
3> X2-22x+4=0
4> x2+x-1=0
5> -x2+x-3=0練習作業三:用配方法求下列方程式之解:
6>x2+5x-3=0
7> x2-4x-9996=0
8> X2-12x - 4=0
9> x2+2x-1=0
10> -x2+3x-3=0練習作業四:用配方法求下列方程式之解:
1>2χ2-5χ+2=0
2>3χ2+4χ+1=0
3>2χ2+5χ+1=0
4>3χ2-2χ-2=0
5>3χ2-18χ-10=0練習作業四:用配方法求下列方程式之解:
6> 9χ2-12χ+1=
7> 2x2-4x-6=0
8> 3X2-12x - 4=0
9> 5x2+2x-1=0
10> -2x2+3x-3=0練習作業一解答:求下列方程式之解:
1>X2=49 ±7
2> X2-9 =0 ±3
3> 5 X2 = 5 ±1
4> 4X2-13=12
5>(X-2)2 = 25 7,-3
6>(3X+2)2 = 2
7>(3X+2)2-49=0
-3,
8>31(2X-5)2 = 0
練習作業二解答:在括號內填入適當的值:
1>X2 +4X+( 4 ) =(X + 2 )2
2> X2-6X+( 9 ) =(X - 3 )2
3> X2 +3X+( ) =(X+ )2
4> X2-5X+( ) =(X - )2
5> Y2 - Y+( ) =(Y - )2 練習作業三解答:用配方法求下列方程式之解:
1>X2+2x-399=0 19,-21
2> X2-6x+5=0 1,5
3> X2-2x-4=0
4> x2+x-1=0
5> -x2+x+3=0練習作業三解答:用配方法求下列方程式之解:
6>x2+4x-5=0 1,-5
7> x2-4x-96=0 12,-8
8> X2-2x-8=0 4,-2
9> x2+2x-1=0
10> -x2+2x+3=0 3,-1練習作業四:用配方法求下列方程式之解:
1>2χ2-5χ+2=0 2,
2>3χ2+4χ+1=0 -1,
3>2χ2+5χ+1=0
4>3χ2-2χ-2=0
5>3χ2-18χ-10=0練習作業四:用配方法求下列方程式之解:
6> 9χ2-12χ+1=0
7> 2x2-4x-6=0 -1,3
8> 3X2-12x - 4=0
9> 5x2+2x-1=0
10> -2x2+3x-1=0 1,
1>X2=49
2> X2-9 =0
3> 5 X2 = 5
4> 4X2 -13 = 12
5>(X -2)2 = 25
6>(3X+2)2 = 2
7>(3X+2)2-49 = 0
8>31(2X-5)2 = 0
練習作業二:在括號內填入適當的值:
1>X2 +4X+( ) =(X+ )2
2> X2-6X+( ) =(X - )2
3> X2 +3X+( ) =(X+ )2
4> X2-5X+( ) =(X - )2
5> Y2 - Y+( ) =(Y - )2 練習作業三:用配方法求下列方程式之解:
1>X2+2x-399=0
2> X2-6x+2=0
3> X2-22x+4=0
4> x2+x-1=0
5> -x2+x-3=0練習作業三:用配方法求下列方程式之解:
6>x2+5x-3=0
7> x2-4x-9996=0
8> X2-12x - 4=0
9> x2+2x-1=0
10> -x2+3x-3=0練習作業四:用配方法求下列方程式之解:
1>2χ2-5χ+2=0
2>3χ2+4χ+1=0
3>2χ2+5χ+1=0
4>3χ2-2χ-2=0
5>3χ2-18χ-10=0練習作業四:用配方法求下列方程式之解:
6> 9χ2-12χ+1=
7> 2x2-4x-6=0
8> 3X2-12x - 4=0
9> 5x2+2x-1=0
10> -2x2+3x-3=0練習作業一解答:求下列方程式之解:
1>X2=49 ±7
2> X2-9 =0 ±3
3> 5 X2 = 5 ±1
4> 4X2-13=12
5>(X-2)2 = 25 7,-3
6>(3X+2)2 = 2
7>(3X+2)2-49=0
-3,
8>31(2X-5)2 = 0
練習作業二解答:在括號內填入適當的值:
1>X2 +4X+( 4 ) =(X + 2 )2
2> X2-6X+( 9 ) =(X - 3 )2
3> X2 +3X+( ) =(X+ )2
4> X2-5X+( ) =(X - )2
5> Y2 - Y+( ) =(Y - )2 練習作業三解答:用配方法求下列方程式之解:
1>X2+2x-399=0 19,-21
2> X2-6x+5=0 1,5
3> X2-2x-4=0
4> x2+x-1=0
5> -x2+x+3=0練習作業三解答:用配方法求下列方程式之解:
6>x2+4x-5=0 1,-5
7> x2-4x-96=0 12,-8
8> X2-2x-8=0 4,-2
9> x2+2x-1=0
10> -x2+2x+3=0 3,-1練習作業四:用配方法求下列方程式之解:
1>2χ2-5χ+2=0 2,
2>3χ2+4χ+1=0 -1,
3>2χ2+5χ+1=0
4>3χ2-2χ-2=0
5>3χ2-18χ-10=0練習作業四:用配方法求下列方程式之解:
6> 9χ2-12χ+1=0
7> 2x2-4x-6=0 -1,3
8> 3X2-12x - 4=0
9> 5x2+2x-1=0
10> -2x2+3x-1=0 1,
同课章节目录
