第13章 三角形中的边角关系 期末复习课件
文档属性
| 名称 | 第13章 三角形中的边角关系 期末复习课件 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 00:00:00 | ||
图片预览



文档简介
(共27张PPT)
第13章 三角形中的边角关系、命题与证明
期末复习(1)
三角形中的边角关系
由不在同一直线上的三条线段首尾
顺次相接所组成的图形叫做三角形.
1.三角形的定义
相邻两边组成的角,叫做三角形的内角,简称三角形的角.
围成三角形的每条线段叫做三角形的边.
每两条线段的交点叫做三角形的顶点.
2.与三角形的有关概念
A
B
C
复习要点
3.三角形的表示
三角形可用符号“△”表示,如下图三角形ABC记作:△ABC. 读作:三角形ABC
复习要点
A
B
C
和垂足的字母.
标明垂直的记号
A
B
C
D
E
F
三角形的高.
复习要点
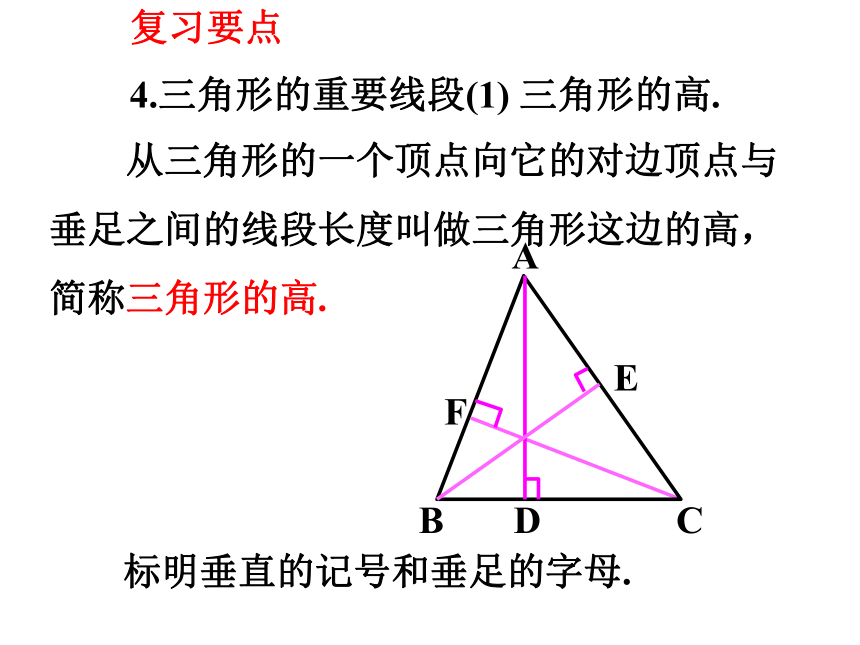
4.三角形的重要线段(1)
从三角形的一个顶点向它的对边顶点与垂足之间的线段长度叫做三角形这边的高,简称三角形的高.
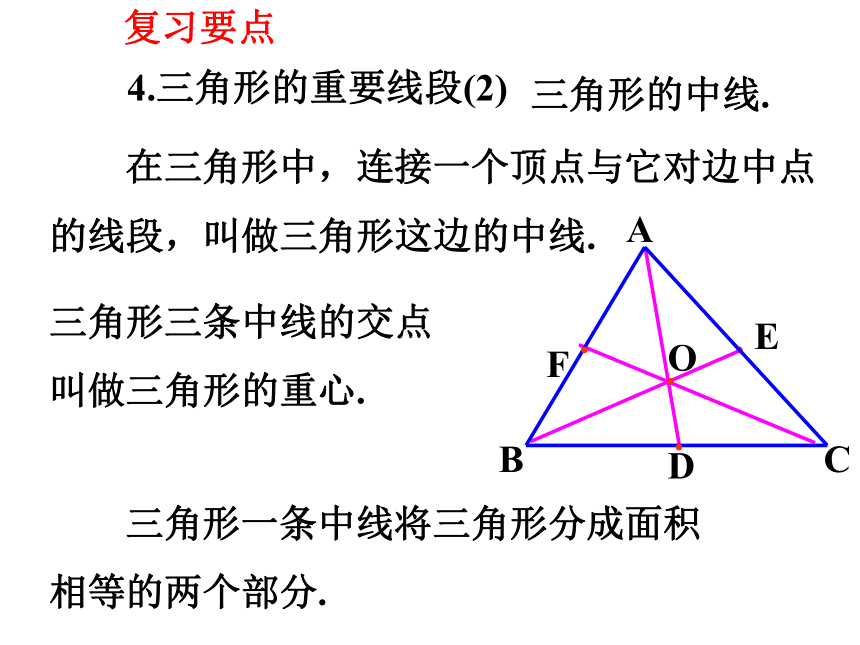
三角形三条中线的交点叫做三角形的重心.
●
A
B
C
D
●
E
F
O
●
●
复习要点
三角形的中线.
4.三角形的重要线段(2)
在三角形中,连接一个顶点与它对边中点的线段,叫做三角形这边的中线.
三角形一条中线将三角形分成面积
相等的两个部分.
A
C
B
F
E
D
O
复习要点
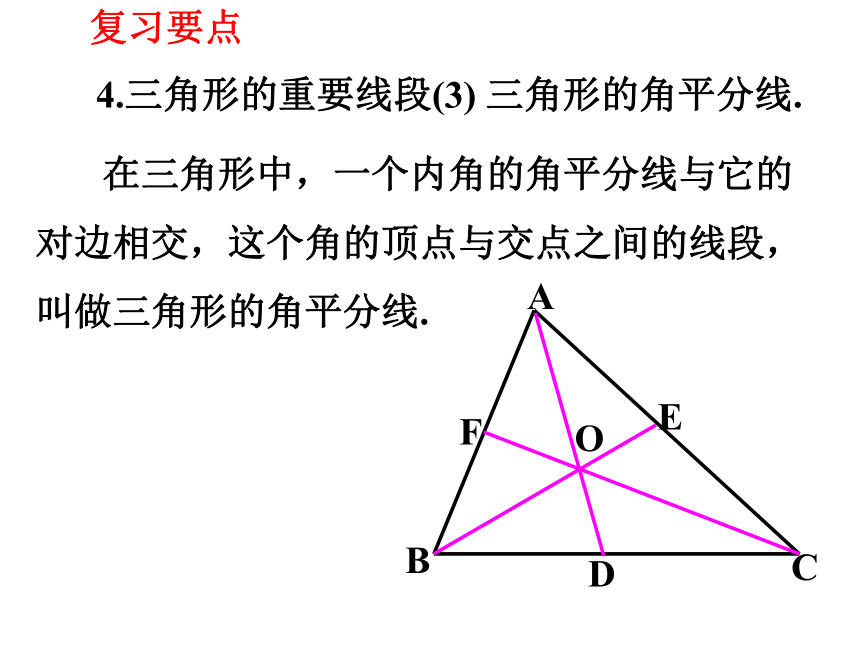
三角形的角平分线.
4.三角形的重要线段(3)
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
A
B
C
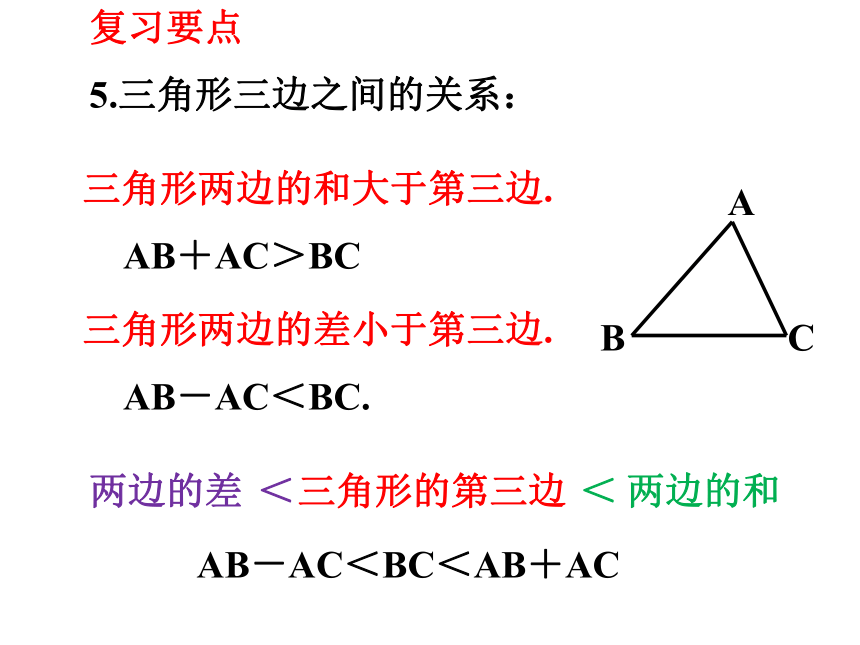
5.三角形三边之间的关系:
三角形两边的差小于第三边.
三角形的第三边
两边的和
两边的差
<
<
复习要点
三角形两边的和大于第三边.
AB+AC>BC
AB-AC<BC.
AB-AC<BC<AB+AC
锐角三角形
直角三角形
钝角三角形
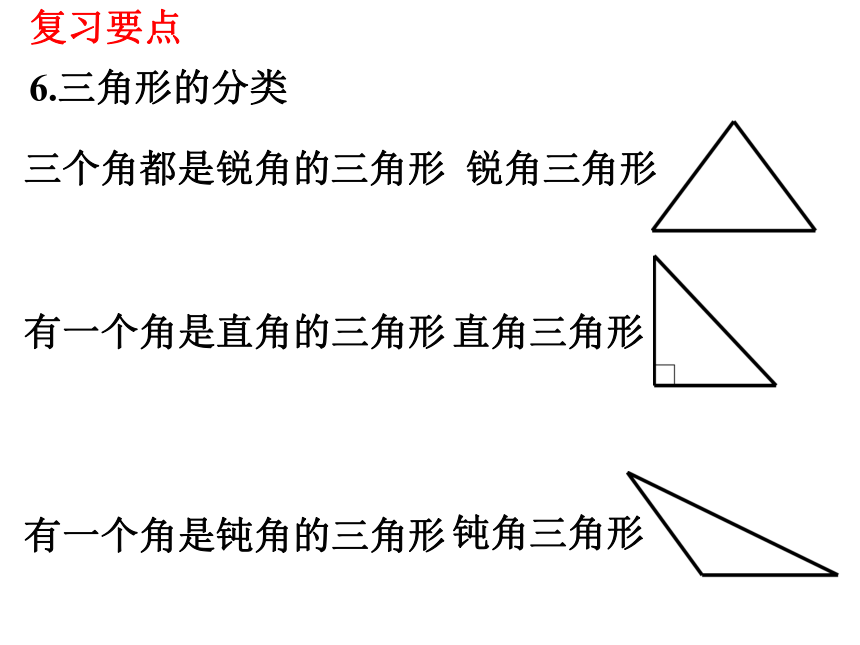
6.三角形的分类
三个角都是锐角的三角形
有一个角是直角的三角形
有一个角是钝角的三角形
复习要点
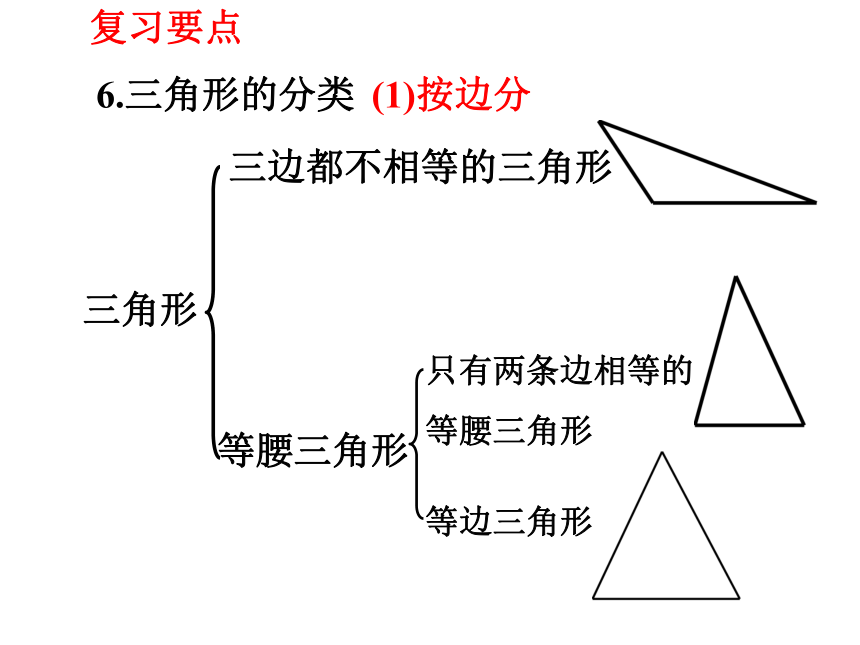
三边都不相等的三角形
等腰三角形
6.三角形的分类
只有两条边相等的等腰三角形
等边三角形
三角形
(1)按边分
复习要点
锐角三角形
直角三角形
钝角三角形
6.三角形的分类
(2)按角分
三角形
斜三角形
复习要点
(1)直角三角形
直角边
AC
直角边BC
斜边AB
直角三角形中夹直角的两边叫做直角边,
直角相对的边叫做斜边.
直角三角形ABC可以写成
Rt△ABC.
A
B
C
复习要点
7.两类重要的三角形
有两条边相等的三角形叫做等腰三角形.
三条边都相等的三角形叫做等边三角形.
在等腰三角形中,相等的两边都叫做腰,
另一边叫做底,
两腰的夹角叫做顶角,
等边三角形是特殊的等腰三角形,
即底边和腰相等的
等腰三角形.
腰
腰
底
顶角
底角
腰和底边的夹角叫底角.
复习要点
(2)等腰三角形
7.两类重要的三角形
A
B
C
8.三角形内角和的结论.
∠A+∠B+∠C=180°.
三角形的内角和等于180°.
复习要点
1.如图,已知△ABC.根据条件画图 ,
并回答问题.
A
B
C
典型例析
(1)画BC边上三的高AD和中线AE.
(2)写出两个以AD为高的三角形.
(3)当AD=5,BE=4时,
△ABC的面积为 .
D
●
E
(2)△ABC,
△AEC.
20
2.如图,AC,BD相交于点O,∠A=54°,∠B=35°, ∠C=42°,求∠D的度数.
A
B
C
D
O
典型例析
∵ ∠A=54°,∠B=35°,
∴∠AOB=
∵∠COD=∠AOB= 91°,
180°- ∠A- ∠B
=180° - 54°-35°
=91°.
解:
∴∠D=
180°- ∠COD- ∠C
=180° -91°-42°
=47°.
3.如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=90°,∠B=32°,
求∠DAE的度数.
A
B
C
D
E
典型例析
∵ ∠BAC=90°,∠B=32°,
∴∠C= 58°.
∵ AD⊥BC,
∴∠ADC= 90°.
∴∠CAD= 32°.
∵ AE是△ABC的角平分线,
∴∠EAC=
∴∠DAE=
∠EAC- ∠CAD
=45°-32°
=13°.
=45°.
∠BAC
1
2
解:
= × 90°
1
2
1.以下列各组线段为边,能组成三角形的是( ).
A. 3 cm ,4 cm,8 cm B. 8 cm,7 cm,15 cm
C. 13 cm,12 cm,20 cm D. 5 cm,5 cm,11 cm
选择题:
2.以长为13cm、10cm、5cm、7cm的四条线段中的
三条线段为边,可以画出三角形的个数是( ).
A.1个 B.2个 C.3个 D.4个
练习巩固
C
C
3.已知三角形的两边长分别为4cm和9cm,则下列
长度的四条线段中能作为第三边的是 ( ).
A.13cm B.6cm C.5cm D.4cm
4.已知等腰三角形的两边长分别为3和6,则它的周长
等于( ).
A. 12 B. 12或15 C. 15 D. 15或18
B
C
5.已知等腰三角形的两边长分别为4和7,则它的周长
等于( ).
A. 11 B. 15 C. 18 D. 15或18
6.等腰三角形的周长为13cm,其中一边长为3cm,则
它的底边长等于( ).
A. 7cm B. 3cm C. 9cm D. 5cm
D
B
7.下面四个图形中,线段BE是△ABC的高的图是( ).
A
B
C
E
A
B
C
E
A
B
C
E
A
B
C
E
A.
B.
C.
D.
8.如图,BD、CE是△ABC的两条高,则∠1与
∠2的大小关系是( ).
A. ∠1 > ∠2 B. ∠1 = ∠2
C. ∠1 < ∠2 D. 不能确定.
A
B
C
E
D
1
2
C
B
9.能将三角形面积平分的线段是三角形的( ).
A. 角平分线 B. 高 C. 中线 D.外角平分线
C
10.如图,在直角三角形ABC中,AC≠AB,AD是斜边上
的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则
图中与∠C(∠C除外)相等的角的个数是( ).
A.3个 B.4个 C.5个 D.6个
A
B
C
E
D
F
A
1.如果一个三角形的三边长度之比是2:3:4,
周长为36cm,则最大的边长为________.
2.在一个直角三角形中,已知一个锐角比另一个锐角
的4倍少15 ,则两个锐角分别为______________.
填空题:
16cm
21
69 、
设较小锐角的度数为x,
较大锐角的度数为y,
x+y =90°
4x-y=15°
3.已知△ABC的两条边长分别为2和5,则第三边长c的
取值范围是 .
4.将长度为a-2,a+5和a+2的三根线段首尾顺次相接
可得到一个三角形,则a的取值范围是 .
3<c<7
a>5
a+5 >
a+2
-(a-2)
a+5 <
a+2
+(a-2)
a>-1
a>5
5.把一副三角板如图所示拼在一起,
那么图中∠AEB是 度.
6.把一副三角板如图所示拼在一起,
则∠AOC+∠BOD是 度.
A
B
C
E
D
A
B
C
D
O
105
180
7.如图,△ABC中,∠A = 30°,∠B = 52°,CE平分
∠ACB,CD⊥AB于D,DF⊥CE,求∠CDF 的度数.
D
A
B
C
E
F
∵ ∠A = 30°,∠B = 52°,
∴ ∠ACB=180°-∠A -∠B = 98°.
∵ CE平分∠ACB,
∴ ∠ECB= ∠ACB = 49°.
∵ CD⊥AB于D,
∵ DF⊥CE,
∴ ∠CDB=90°,
∴ ∠BCD +∠B=90°.
∴ ∠BCD=90° -∠B = 90°-52°=38°.
∴ ∠CFD=90°,
∴ ∠CDF=90° -∠DCE = 90°-11°=79°.
∴ ∠DCE=90° -∠B = 90°-52°=38°.
解:
1
2
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第13章 三角形中的边角关系、命题与证明
期末复习(1)
三角形中的边角关系
由不在同一直线上的三条线段首尾
顺次相接所组成的图形叫做三角形.
1.三角形的定义
相邻两边组成的角,叫做三角形的内角,简称三角形的角.
围成三角形的每条线段叫做三角形的边.
每两条线段的交点叫做三角形的顶点.
2.与三角形的有关概念
A
B
C
复习要点
3.三角形的表示
三角形可用符号“△”表示,如下图三角形ABC记作:△ABC. 读作:三角形ABC
复习要点
A
B
C
和垂足的字母.
标明垂直的记号
A
B
C
D
E
F
三角形的高.
复习要点
4.三角形的重要线段(1)
从三角形的一个顶点向它的对边顶点与垂足之间的线段长度叫做三角形这边的高,简称三角形的高.
三角形三条中线的交点叫做三角形的重心.
●
A
B
C
D
●
E
F
O
●
●
复习要点
三角形的中线.
4.三角形的重要线段(2)
在三角形中,连接一个顶点与它对边中点的线段,叫做三角形这边的中线.
三角形一条中线将三角形分成面积
相等的两个部分.
A
C
B
F
E
D
O
复习要点
三角形的角平分线.
4.三角形的重要线段(3)
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
A
B
C
5.三角形三边之间的关系:
三角形两边的差小于第三边.
三角形的第三边
两边的和
两边的差
<
<
复习要点
三角形两边的和大于第三边.
AB+AC>BC
AB-AC<BC.
AB-AC<BC<AB+AC
锐角三角形
直角三角形
钝角三角形
6.三角形的分类
三个角都是锐角的三角形
有一个角是直角的三角形
有一个角是钝角的三角形
复习要点
三边都不相等的三角形
等腰三角形
6.三角形的分类
只有两条边相等的等腰三角形
等边三角形
三角形
(1)按边分
复习要点
锐角三角形
直角三角形
钝角三角形
6.三角形的分类
(2)按角分
三角形
斜三角形
复习要点
(1)直角三角形
直角边
AC
直角边BC
斜边AB
直角三角形中夹直角的两边叫做直角边,
直角相对的边叫做斜边.
直角三角形ABC可以写成
Rt△ABC.
A
B
C
复习要点
7.两类重要的三角形
有两条边相等的三角形叫做等腰三角形.
三条边都相等的三角形叫做等边三角形.
在等腰三角形中,相等的两边都叫做腰,
另一边叫做底,
两腰的夹角叫做顶角,
等边三角形是特殊的等腰三角形,
即底边和腰相等的
等腰三角形.
腰
腰
底
顶角
底角
腰和底边的夹角叫底角.
复习要点
(2)等腰三角形
7.两类重要的三角形
A
B
C
8.三角形内角和的结论.
∠A+∠B+∠C=180°.
三角形的内角和等于180°.
复习要点
1.如图,已知△ABC.根据条件画图 ,
并回答问题.
A
B
C
典型例析
(1)画BC边上三的高AD和中线AE.
(2)写出两个以AD为高的三角形.
(3)当AD=5,BE=4时,
△ABC的面积为 .
D
●
E
(2)△ABC,
△AEC.
20
2.如图,AC,BD相交于点O,∠A=54°,∠B=35°, ∠C=42°,求∠D的度数.
A
B
C
D
O
典型例析
∵ ∠A=54°,∠B=35°,
∴∠AOB=
∵∠COD=∠AOB= 91°,
180°- ∠A- ∠B
=180° - 54°-35°
=91°.
解:
∴∠D=
180°- ∠COD- ∠C
=180° -91°-42°
=47°.
3.如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=90°,∠B=32°,
求∠DAE的度数.
A
B
C
D
E
典型例析
∵ ∠BAC=90°,∠B=32°,
∴∠C= 58°.
∵ AD⊥BC,
∴∠ADC= 90°.
∴∠CAD= 32°.
∵ AE是△ABC的角平分线,
∴∠EAC=
∴∠DAE=
∠EAC- ∠CAD
=45°-32°
=13°.
=45°.
∠BAC
1
2
解:
= × 90°
1
2
1.以下列各组线段为边,能组成三角形的是( ).
A. 3 cm ,4 cm,8 cm B. 8 cm,7 cm,15 cm
C. 13 cm,12 cm,20 cm D. 5 cm,5 cm,11 cm
选择题:
2.以长为13cm、10cm、5cm、7cm的四条线段中的
三条线段为边,可以画出三角形的个数是( ).
A.1个 B.2个 C.3个 D.4个
练习巩固
C
C
3.已知三角形的两边长分别为4cm和9cm,则下列
长度的四条线段中能作为第三边的是 ( ).
A.13cm B.6cm C.5cm D.4cm
4.已知等腰三角形的两边长分别为3和6,则它的周长
等于( ).
A. 12 B. 12或15 C. 15 D. 15或18
B
C
5.已知等腰三角形的两边长分别为4和7,则它的周长
等于( ).
A. 11 B. 15 C. 18 D. 15或18
6.等腰三角形的周长为13cm,其中一边长为3cm,则
它的底边长等于( ).
A. 7cm B. 3cm C. 9cm D. 5cm
D
B
7.下面四个图形中,线段BE是△ABC的高的图是( ).
A
B
C
E
A
B
C
E
A
B
C
E
A
B
C
E
A.
B.
C.
D.
8.如图,BD、CE是△ABC的两条高,则∠1与
∠2的大小关系是( ).
A. ∠1 > ∠2 B. ∠1 = ∠2
C. ∠1 < ∠2 D. 不能确定.
A
B
C
E
D
1
2
C
B
9.能将三角形面积平分的线段是三角形的( ).
A. 角平分线 B. 高 C. 中线 D.外角平分线
C
10.如图,在直角三角形ABC中,AC≠AB,AD是斜边上
的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则
图中与∠C(∠C除外)相等的角的个数是( ).
A.3个 B.4个 C.5个 D.6个
A
B
C
E
D
F
A
1.如果一个三角形的三边长度之比是2:3:4,
周长为36cm,则最大的边长为________.
2.在一个直角三角形中,已知一个锐角比另一个锐角
的4倍少15 ,则两个锐角分别为______________.
填空题:
16cm
21
69 、
设较小锐角的度数为x,
较大锐角的度数为y,
x+y =90°
4x-y=15°
3.已知△ABC的两条边长分别为2和5,则第三边长c的
取值范围是 .
4.将长度为a-2,a+5和a+2的三根线段首尾顺次相接
可得到一个三角形,则a的取值范围是 .
3<c<7
a>5
a+5 >
a+2
-(a-2)
a+5 <
a+2
+(a-2)
a>-1
a>5
5.把一副三角板如图所示拼在一起,
那么图中∠AEB是 度.
6.把一副三角板如图所示拼在一起,
则∠AOC+∠BOD是 度.
A
B
C
E
D
A
B
C
D
O
105
180
7.如图,△ABC中,∠A = 30°,∠B = 52°,CE平分
∠ACB,CD⊥AB于D,DF⊥CE,求∠CDF 的度数.
D
A
B
C
E
F
∵ ∠A = 30°,∠B = 52°,
∴ ∠ACB=180°-∠A -∠B = 98°.
∵ CE平分∠ACB,
∴ ∠ECB= ∠ACB = 49°.
∵ CD⊥AB于D,
∵ DF⊥CE,
∴ ∠CDB=90°,
∴ ∠BCD +∠B=90°.
∴ ∠BCD=90° -∠B = 90°-52°=38°.
∴ ∠CFD=90°,
∴ ∠CDF=90° -∠DCE = 90°-11°=79°.
∴ ∠DCE=90° -∠B = 90°-52°=38°.
解:
1
2
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
