18.2.3正方形课件

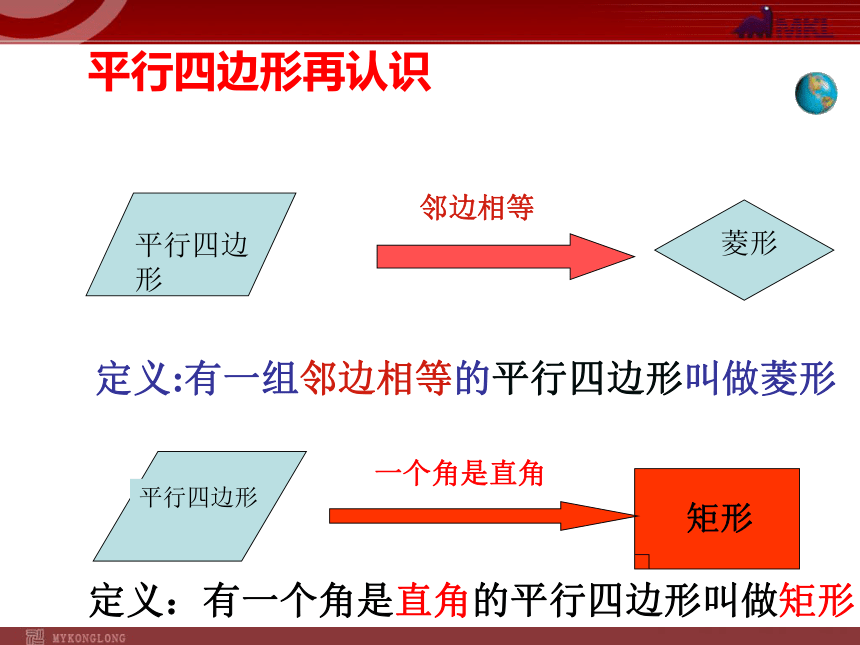
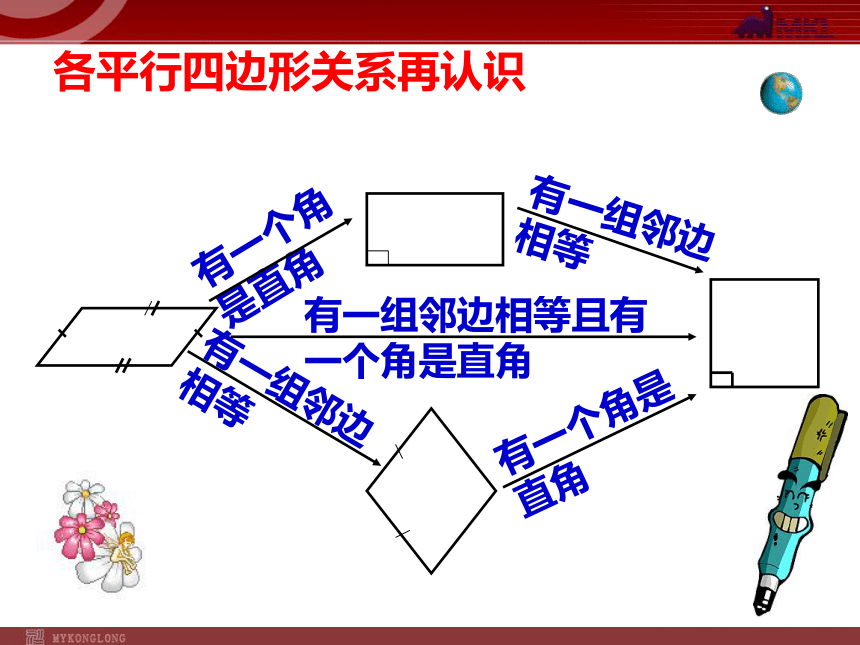
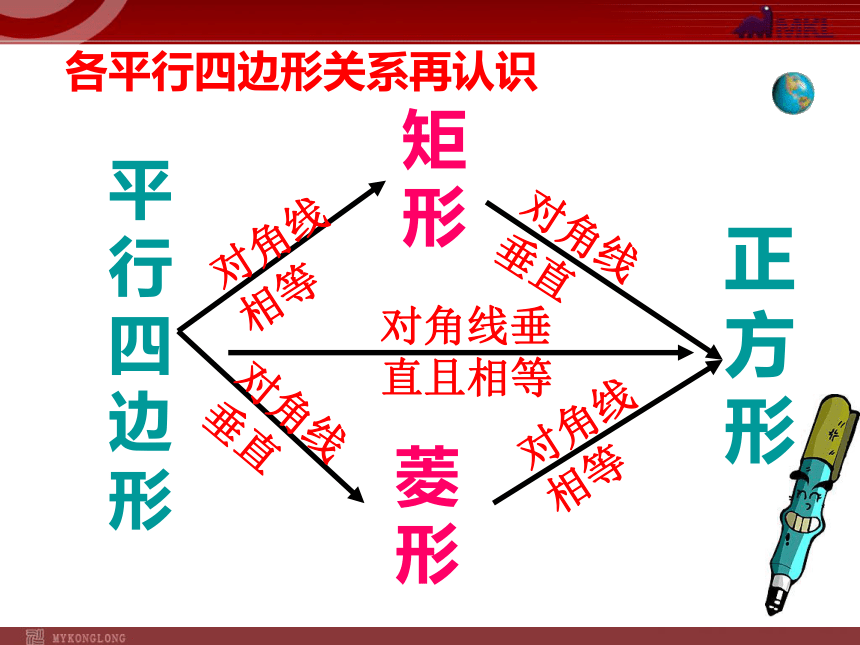
课件20张PPT。18.2特殊的平行四边形18.2.3正方形平行四边形再认识定义:有一组邻边相等的平行四边形叫做菱形一个角是直角定义：有一个角是直角的平行四边形叫做矩形邻边相等平行四边形再认识平行四边形、矩形、菱形、正方形的关系正方形⑴有一组邻边相等的平行四边形（菱形） ⑵并且有一个角是直角的平行四边形（矩形）两层含义正方形换句话：有一组邻边相等并且有一个角是直角的平行四边形 有一组邻边相等的矩形叫做正方形正方形定义:正方形再认识有一个角是直角有一组邻边相等有一组邻边相等有一个角是直角有一组邻边相等且有一个角是直角各平行四边形关系再认识平行四边形矩形菱形正方形对角线相等对角线垂直对角线相等对角线垂直对角线垂直且相等各平行四边形关系再认识正方形的性质边对角线对边平行四边相等对角线相等 互相垂直平分每条对角线平分一组对角四个角相等且都是直角角: 正方形性质所以：正方形不仅是平行四边形、矩形，还是菱形。正方形的性质正方形的判定定理:有一个角是直角的菱形是正方形.求证:四边形ABCD是正方形.分析:要证明四边形ABCD是正方形,可转化为证明有一组邻边相等的矩形即可.证明:∴AB=BC,∠C=∠A=900,∠B=1800-∠A=900.∴∠A=∠B=∠C=900.∴四边形ABCD是矩形.∵四边形ABCD是菱形,∠A=900,∵AB=BC,∴四边形ABCD是正方形.已知:四边形ABCD是菱形,∠A=900.定理:对角线相等的菱形是正方形.求证:四边形ABCD是正方形.分析:要证明四边形ABCD是正方形,可转化为证明有一组邻边相等的矩形(或有一个角是直角的菱形)即可.证明:∴AB=BC,四边形ABCD是平行四边形.∵AC=BD,∴四边形ABCD是矩形.∵AB=BC,∵四边形ABCD是菱形,∴四边形ABCD是正方形.已知:四边形ABCD是菱形,且对角线AC=BD.正方形的判定定理:对角线互相垂直的矩形是正方形.求证:四边形ABCD是正方形.分析:要证明四边形ABCD是正方形,可转化为证明有一角是直角的菱形(或有一组邻边相等的矩形,或对角线相等的菱形)即可.证明:∴∠ABC=900,四边形ABCD是平行四边形.∵AC⊥BD,∴四边形ABCD是菱形.∵∠ABC=900.∵四边形ABCD是矩形,∴四边形ABCD是正方形.已知:四边形ABCD是矩形,且AC⊥BD.正方形的判定(2)若AC=4，则正方形边长 ; 正方形的面积是四边形ABCD是正方形,两条对角线相交于点O,(1)求∠AOB,∠OAB的度数。8解：
（1）∵四边形ABCD是正方形
∴AC⊥BD　∠AOB=900
∠BAC=∠DAC
∴∠OAB=450 4㎝(3)正方形的面积64cm，则对角线交点到正方形一边的距离四边形再认识猜一猜 AC为正方形ABCD的对角线，E为AC上一点，且AB=AE，EF⊥AC交BC于F，求证：EC=EF=FBABCDEF┌证明： ∵ 四边形ABCD是正方形
∴∠B=900 ∠ACB=450
∵∠AEF=900 AB=AE
∴△ABF≌△AFE（HL）
∴BF=EF
又∵∠FEC=900
∴∠EFC=450
∴EC=EF（等角对等边）
∴BF=EF=EC构建与证明OBA如图，分别延长等腰直角三角形OAB的两条直角边AO和BO，使AO=OC，BO=OD
求证：四边形ABCD是正方形。轴对称 在一块正方形的花坛上，欲修建两条直的小路，使得两条直的小路将花坛平均分成面积相等的四部分（不考虑道路的宽度），你有几种方法？（至少说出三种）
思维拓展如何设计花坛？数一数图中正方形的个数，你发现了什么？多多多 （　）个（　）个　　（　）个　　　　 （　）个第n个图中正方形有 个3n-1长见识学习了本节课你有哪些收获？