安徽省黄山市八校联盟2023-2024学年高二上学期期中考试数学试题(含答案)
文档属性
| 名称 | 安徽省黄山市八校联盟2023-2024学年高二上学期期中考试数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 17:37:35 | ||
图片预览




文档简介
“八校联盟”2023-2024学年度第一学期期中考试
高二数学试题
(考试时间:120分钟 满分:150分)
注意事项:
1. 答卷前,考生务必将自己的姓名、准考证号填涂在答题卡上.
2. 选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号.写在试卷上无效.
3. 非选择题必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设点关于坐标原点的对称点是B,则等于
A.6 B. C. D.
2. 设为定点,,动点 满足 ,则动点的轨迹是
A. 线段 B. 直线 C. 圆 D. 椭圆
3. 已知直线l的一个方向向量为,直线l的倾斜角为,则的值为
A. B. 0 C. D. 2
4. 设,则是直线与直线平行的
A. 必要不充分条件 B. 充分不必要条件
C. 充要条件 D. 既不充分也不必要条件
5. 已知点D在△ABC确定的平面内,O是平面ABC外任意一点,实数x,y满足,则的最小值为
A. B. C. 1 D.
6. 已知P是直线l:上一动点,过点P作圆C:的两条切线,切点分别为A、B,则四边形PACB的外接圆的面积的最小值为
A. B. C. D.
7. 已知矩形的四个顶点都在椭圆 上,边和分别经过椭圆的左、右焦点,且,则该椭圆的离心率
A. B. C. D.
8. 《九章算术》是我国古代数学名著。书中将底面为矩形,
且有一条侧棱垂直于底面的四棱锥称为阳马。如图,在
阳马中,PA⊥平面ABCD,底面ABCD是矩形,
E、F分别为PD,PB的中点,,,
,若AG⊥平面EFC,则=
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 下列说法正确的是
A.点关于直线的对称点为
B.过,两点的直线方程为
C.经过点且在轴和轴上截距都相等的直线方程为
D.直线与两坐标轴围成的三角形的面积是2
10. 如图,直三棱柱中,,,D、E分别为、的中点,则下列结论正确的是
A. ∥
B. 直线DE与平面所成角的正弦值为
C. 平面与平面ABC夹角的余弦值为
D. DE与所成角为
11. 已知AC为圆锥SO底面圆O的直径,,,点B为圆O上异于A、C的一点,M为线段SC上的动点(异于端点),则
A. 直线SB与平面SAM所成角的最大值为
B. 圆锥SO内切球的体积为
C. 棱长为的正四面体可以放在圆锥SO内
D. 当M为SC的中点时,满足的点B有2个
12. 如图所示。已知椭圆方程为,
F1、F2为左右焦点,下列命题正确的是
A. P为椭圆上一点,线段PF1中点为Q,则
为定值
B.直线与椭圆交于R , S两点,A是椭圆上异与R , S的点,且、均存在,则
C.若椭圆上存在一点M使,则椭圆离心率的取值范围是
D.四边形ABCD为椭圆内接矩形,则其面积最大值为2ab
三、填空题:本题共4小题,每小题5分,共20分.
13. 已知空间向量,,则向量在向量上的投影向量的坐标是
.
14. 已知P为圆上一点,则点到P点的距离的最大值为 .
15. 若关于的不等式的解集是,则值是________.
16. 半径为R的球面上有A、B、C、D四个点,,则的最大值为
.
四、解答题:本题共6小题,共70分. 解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
如图,三棱锥中,点D、E分别为和的中点,设,,.
(1)试用,,表示向量;
(2)若,,求异面直线AE与CD所成角的余弦值.
18.(本小题满分12分)
已知直线.
①若直线l不经过第二象限,求k的取值范围.
②若直线l与x轴、y轴正半轴分别交于A、B两点,当△AOB的面积为时(O为坐标原点),求此时相应的直线l的方程.
19.(本小题满分12分)
如图,△与△都是边长为2的正三角形,平面ABD平面ABC,EC平面ABC且.
(1)证明:CD平面ABE
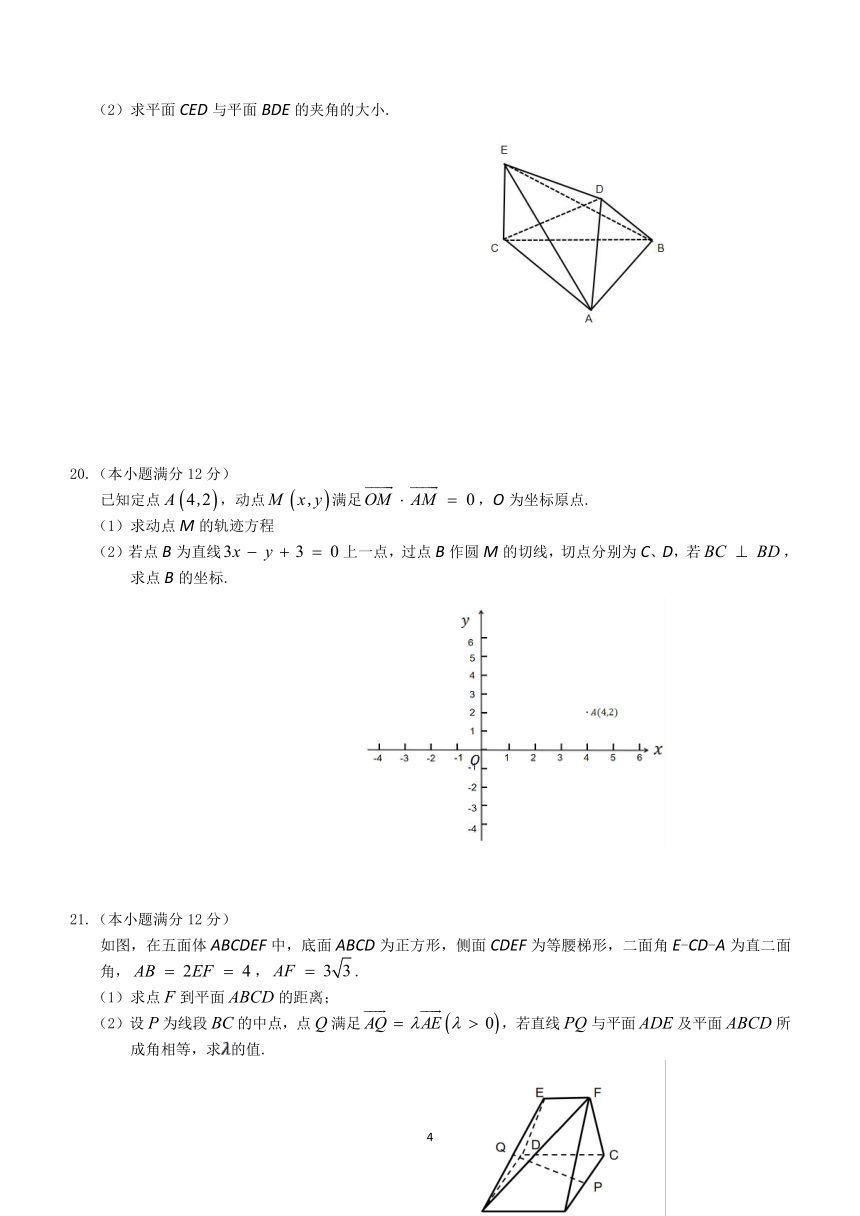
(2)求平面CED与平面BDE的夹角的大小.
20.(本小题满分12分)
已知定点,动点满足,O为坐标原点.
(1)求动点M的轨迹方程
(2)若点B为直线上一点,过点B作圆M的切线,切点分别为C、D,若,求点B的坐标.
21.(本小题满分12分)
如图,在五面体ABCDEF中,底面ABCD为正方形,侧面CDEF为等腰梯形,二面角E-CD-A为直二面角,,.
(1)求点F到平面ABCD的距离;
(2)设P为线段BC的中点,点Q满足,若直线PQ与平面ADE及平面ABCD所成角相等,求的值.
22.(本小题满分12分)
椭圆的左右焦点分别为、,短轴端点分别为、.若四边
形为正方形,且.
(1)求椭圆标准方程;
(2)若、分别是椭圆长轴左、右端点,动点满足,点在椭圆上,且满足,求证定值(为坐标原点);
(3)在(2)条件下,试问在轴上是否存在异于点的定点,使,若存在,求坐标,若不存在,说明理由.
“八校联盟”2023-2024学年度第一学期高二期中考试
数学试题参考答案及评分标准
一、单项选择题:本题共8小题,每小题5分,共40分.
题号 1 2 3 4 5 6 7 8
答案 C A A B D B A C
二、多项选择题:本题共4小题,每小题5分,共20分.
题号 9 10 11 12
答案 AD ABC AC ACD
三、填空题:本题共4小题,每小题5分,共20分.
13. () 14. 8 15. 2 16.
四、解答题:本题共6小题,共70分. 解答应写出文字说明、证明过程或演算步骤.
17.解:(1)
…………………………………………………………………………4分
(2)由题意可得:
………………………………………………………………………………5分
………………………………………………………………………………6分
…………………………………………………………………………………………………8分
………………………9分
∴异面直线AE和CD所成角的余弦值为. …………………………10分
18.解:(1)解:由题意可知直线l:y=kx-2k+1 (k)
y=k(x-2)+1 易知直线l过定点(2,1) ………………………………………………2分
当直线l过原点时,可得k=
当k≥时,直线l不经过第二象限. ……………………………………………………4分
(2)解: 由题意可知k0, ∵直线l:y=kx-2k+1与x轴、y轴正半轴的交点分别是
A(2 , 0),B(0,1-2k) ………………………………………………………6分
SΔAOB=|2-||1-2k|= ……………………………………………………7分
当k0时,由SΔAOB=得:
= [(-4k+)+4]=
即:4k2+5k+1=0
∴k=-1或k= - ………………………………………………………………………10分
即:直线l的方程为y=-x+3或y=-x+ …………………………………………………12分
19.解:证明:取AB中点F,连接CF,DF
∵ΔABC,ΔABD都是正三角形
∴AB⊥CF,AB⊥DF,又CF∩DF=F
∴AB⊥面CDF
∴AB⊥CD …………………………………………………………………………………………2分
又平面ABC⊥平面ABD
∴DF⊥面ABC DF= …………………………………………………………………………………3分
又CE⊥面DBC 且EC=
∵DF∥CE DF =CE DF⊥CF
∵CFDE是正方形 ∴CD⊥EF ………………………………………………………………………5分
又EF∩AB=F ∴CD⊥平面ABE. …………………………………………………………………6分
(2)由(1)知AB、CF,DF两两重直,
如图建立空间直角坐标系由于x轴垂直面CEDF
∴平面CDE的法向量为 ………………7分
又 B(1,0,0) D(0,0, ) E(O, ,)
∴=(-1,0,) =(-1, ,) ………8分
设平面BDE的法向量n=(x,y,z)
则
令x=,n=(,0,1) ……………………………………………………………………10分
∴
∴平面CDE与平面BDE的夹角为 …………………………………………………………………12分
20. 解:(1)由题意得:=(x,y)=(x-4,y-2)
∴
……………………………………………………2分
即
∴M的轨迹方程为 ………………………………………………4分
(2)由题意可知:B为直线3x-y+3=0上一点,又BC、BD分别与圆M相切于点C、D,且BC⊥BD.
连接MC、MD,易知四边形BCMD为正方形. ………………………………………6分
∵四边形BCMD为正方形,且|MC|=|MD|=|BC|=|BD|=
∴|BM|= ………………………8分
设B(x,y),则:
……………9分
解得或 ……………11分
∴B点的坐标为 或 ……………………………………………………12分
21.解:(1) 如图,过点F作FODC于点O,连接OA.
因为二面角ECDA为直二面角,所以平面CDEF平面ABCD,
又平面CDEF平面ABCD=CD,FO平面CDE,所以FO平面ABCD,
因为OA平面ABCD,所以FOOA. ………………………………………………………………2分
因为四边形CDEF为等腰梯形,AB=CD=2EF=4,
所以OD=3,所以AO=5 …………………………………………………………………4分
又AF=3,所以FO=,即点F到平面ABCD的距离为. ………………………………5分
(2) 以O为坐标原点,分别以OD,OF所在直线分别为x,z轴,过点O作平面CDEF的垂线为y轴,建立如图所示的空间直角坐标系.
则A(3,4,0),D(3,0,0),E(2,0,),
F(0,0,),P(-1,2,0), ………………………………6分
由==(-,-4,),得Q(3-,4-4,),
∴=(4-,2-4,), ……………………………7分
设平面ADE的法向量为n=(x,y,),由=(0,4,0),
=(-1,0,),,得,
令z=1,则n=(,0,1). ……………………………………………………………………9分
又易知平面ABCD的一个法向量m=(,0,1). …………………………………………10分
设直线PQ与平面ADE所成角为,与平面ABCD所成角为,
则,∴=, …………………………………………………………11分
整理得=,由=. …………………………………………………………12分
22.解:(1)依题证得且,∴ ………………………………2分
故椭圆方程为 ……………………………………………………………3分
②设方程为
联立方程组可得
解得 ……………………5分
∵ ∴P、C、M三点共线.
∴ ……………………………6分
又由得:.=0 即:MDDC
∴联立方程组可得 …………………………………………………7分
定值 ………………………………………………………9分
③设
…………………………………………………………………………10分
∴得
故 ……………………………………………………………………………………11分
也就是说存在一点满足条件. ……………12分
第8题图
第10题图
第12题图
O
高二数学试题
(考试时间:120分钟 满分:150分)
注意事项:
1. 答卷前,考生务必将自己的姓名、准考证号填涂在答题卡上.
2. 选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号.写在试卷上无效.
3. 非选择题必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设点关于坐标原点的对称点是B,则等于
A.6 B. C. D.
2. 设为定点,,动点 满足 ,则动点的轨迹是
A. 线段 B. 直线 C. 圆 D. 椭圆
3. 已知直线l的一个方向向量为,直线l的倾斜角为,则的值为
A. B. 0 C. D. 2
4. 设,则是直线与直线平行的
A. 必要不充分条件 B. 充分不必要条件
C. 充要条件 D. 既不充分也不必要条件
5. 已知点D在△ABC确定的平面内,O是平面ABC外任意一点,实数x,y满足,则的最小值为
A. B. C. 1 D.
6. 已知P是直线l:上一动点,过点P作圆C:的两条切线,切点分别为A、B,则四边形PACB的外接圆的面积的最小值为
A. B. C. D.
7. 已知矩形的四个顶点都在椭圆 上,边和分别经过椭圆的左、右焦点,且,则该椭圆的离心率
A. B. C. D.
8. 《九章算术》是我国古代数学名著。书中将底面为矩形,
且有一条侧棱垂直于底面的四棱锥称为阳马。如图,在
阳马中,PA⊥平面ABCD,底面ABCD是矩形,
E、F分别为PD,PB的中点,,,
,若AG⊥平面EFC,则=
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 下列说法正确的是
A.点关于直线的对称点为
B.过,两点的直线方程为
C.经过点且在轴和轴上截距都相等的直线方程为
D.直线与两坐标轴围成的三角形的面积是2
10. 如图,直三棱柱中,,,D、E分别为、的中点,则下列结论正确的是
A. ∥
B. 直线DE与平面所成角的正弦值为
C. 平面与平面ABC夹角的余弦值为
D. DE与所成角为
11. 已知AC为圆锥SO底面圆O的直径,,,点B为圆O上异于A、C的一点,M为线段SC上的动点(异于端点),则
A. 直线SB与平面SAM所成角的最大值为
B. 圆锥SO内切球的体积为
C. 棱长为的正四面体可以放在圆锥SO内
D. 当M为SC的中点时,满足的点B有2个
12. 如图所示。已知椭圆方程为,
F1、F2为左右焦点,下列命题正确的是
A. P为椭圆上一点,线段PF1中点为Q,则
为定值
B.直线与椭圆交于R , S两点,A是椭圆上异与R , S的点,且、均存在,则
C.若椭圆上存在一点M使,则椭圆离心率的取值范围是
D.四边形ABCD为椭圆内接矩形,则其面积最大值为2ab
三、填空题:本题共4小题,每小题5分,共20分.
13. 已知空间向量,,则向量在向量上的投影向量的坐标是
.
14. 已知P为圆上一点,则点到P点的距离的最大值为 .
15. 若关于的不等式的解集是,则值是________.
16. 半径为R的球面上有A、B、C、D四个点,,则的最大值为
.
四、解答题:本题共6小题,共70分. 解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
如图,三棱锥中,点D、E分别为和的中点,设,,.
(1)试用,,表示向量;
(2)若,,求异面直线AE与CD所成角的余弦值.
18.(本小题满分12分)
已知直线.
①若直线l不经过第二象限,求k的取值范围.
②若直线l与x轴、y轴正半轴分别交于A、B两点,当△AOB的面积为时(O为坐标原点),求此时相应的直线l的方程.
19.(本小题满分12分)
如图,△与△都是边长为2的正三角形,平面ABD平面ABC,EC平面ABC且.
(1)证明:CD平面ABE
(2)求平面CED与平面BDE的夹角的大小.
20.(本小题满分12分)
已知定点,动点满足,O为坐标原点.
(1)求动点M的轨迹方程
(2)若点B为直线上一点,过点B作圆M的切线,切点分别为C、D,若,求点B的坐标.
21.(本小题满分12分)
如图,在五面体ABCDEF中,底面ABCD为正方形,侧面CDEF为等腰梯形,二面角E-CD-A为直二面角,,.
(1)求点F到平面ABCD的距离;
(2)设P为线段BC的中点,点Q满足,若直线PQ与平面ADE及平面ABCD所成角相等,求的值.
22.(本小题满分12分)
椭圆的左右焦点分别为、,短轴端点分别为、.若四边
形为正方形,且.
(1)求椭圆标准方程;
(2)若、分别是椭圆长轴左、右端点,动点满足,点在椭圆上,且满足,求证定值(为坐标原点);
(3)在(2)条件下,试问在轴上是否存在异于点的定点,使,若存在,求坐标,若不存在,说明理由.
“八校联盟”2023-2024学年度第一学期高二期中考试
数学试题参考答案及评分标准
一、单项选择题:本题共8小题,每小题5分,共40分.
题号 1 2 3 4 5 6 7 8
答案 C A A B D B A C
二、多项选择题:本题共4小题,每小题5分,共20分.
题号 9 10 11 12
答案 AD ABC AC ACD
三、填空题:本题共4小题,每小题5分,共20分.
13. () 14. 8 15. 2 16.
四、解答题:本题共6小题,共70分. 解答应写出文字说明、证明过程或演算步骤.
17.解:(1)
…………………………………………………………………………4分
(2)由题意可得:
………………………………………………………………………………5分
………………………………………………………………………………6分
…………………………………………………………………………………………………8分
………………………9分
∴异面直线AE和CD所成角的余弦值为. …………………………10分
18.解:(1)解:由题意可知直线l:y=kx-2k+1 (k)
y=k(x-2)+1 易知直线l过定点(2,1) ………………………………………………2分
当直线l过原点时,可得k=
当k≥时,直线l不经过第二象限. ……………………………………………………4分
(2)解: 由题意可知k0, ∵直线l:y=kx-2k+1与x轴、y轴正半轴的交点分别是
A(2 , 0),B(0,1-2k) ………………………………………………………6分
SΔAOB=|2-||1-2k|= ……………………………………………………7分
当k0时,由SΔAOB=得:
= [(-4k+)+4]=
即:4k2+5k+1=0
∴k=-1或k= - ………………………………………………………………………10分
即:直线l的方程为y=-x+3或y=-x+ …………………………………………………12分
19.解:证明:取AB中点F,连接CF,DF
∵ΔABC,ΔABD都是正三角形
∴AB⊥CF,AB⊥DF,又CF∩DF=F
∴AB⊥面CDF
∴AB⊥CD …………………………………………………………………………………………2分
又平面ABC⊥平面ABD
∴DF⊥面ABC DF= …………………………………………………………………………………3分
又CE⊥面DBC 且EC=
∵DF∥CE DF =CE DF⊥CF
∵CFDE是正方形 ∴CD⊥EF ………………………………………………………………………5分
又EF∩AB=F ∴CD⊥平面ABE. …………………………………………………………………6分
(2)由(1)知AB、CF,DF两两重直,
如图建立空间直角坐标系由于x轴垂直面CEDF
∴平面CDE的法向量为 ………………7分
又 B(1,0,0) D(0,0, ) E(O, ,)
∴=(-1,0,) =(-1, ,) ………8分
设平面BDE的法向量n=(x,y,z)
则
令x=,n=(,0,1) ……………………………………………………………………10分
∴
∴平面CDE与平面BDE的夹角为 …………………………………………………………………12分
20. 解:(1)由题意得:=(x,y)=(x-4,y-2)
∴
……………………………………………………2分
即
∴M的轨迹方程为 ………………………………………………4分
(2)由题意可知:B为直线3x-y+3=0上一点,又BC、BD分别与圆M相切于点C、D,且BC⊥BD.
连接MC、MD,易知四边形BCMD为正方形. ………………………………………6分
∵四边形BCMD为正方形,且|MC|=|MD|=|BC|=|BD|=
∴|BM|= ………………………8分
设B(x,y),则:
……………9分
解得或 ……………11分
∴B点的坐标为 或 ……………………………………………………12分
21.解:(1) 如图,过点F作FODC于点O,连接OA.
因为二面角ECDA为直二面角,所以平面CDEF平面ABCD,
又平面CDEF平面ABCD=CD,FO平面CDE,所以FO平面ABCD,
因为OA平面ABCD,所以FOOA. ………………………………………………………………2分
因为四边形CDEF为等腰梯形,AB=CD=2EF=4,
所以OD=3,所以AO=5 …………………………………………………………………4分
又AF=3,所以FO=,即点F到平面ABCD的距离为. ………………………………5分
(2) 以O为坐标原点,分别以OD,OF所在直线分别为x,z轴,过点O作平面CDEF的垂线为y轴,建立如图所示的空间直角坐标系.
则A(3,4,0),D(3,0,0),E(2,0,),
F(0,0,),P(-1,2,0), ………………………………6分
由==(-,-4,),得Q(3-,4-4,),
∴=(4-,2-4,), ……………………………7分
设平面ADE的法向量为n=(x,y,),由=(0,4,0),
=(-1,0,),,得,
令z=1,则n=(,0,1). ……………………………………………………………………9分
又易知平面ABCD的一个法向量m=(,0,1). …………………………………………10分
设直线PQ与平面ADE所成角为,与平面ABCD所成角为,
则,∴=, …………………………………………………………11分
整理得=,由=. …………………………………………………………12分
22.解:(1)依题证得且,∴ ………………………………2分
故椭圆方程为 ……………………………………………………………3分
②设方程为
联立方程组可得
解得 ……………………5分
∵ ∴P、C、M三点共线.
∴ ……………………………6分
又由得:.=0 即:MDDC
∴联立方程组可得 …………………………………………………7分
定值 ………………………………………………………9分
③设
…………………………………………………………………………10分
∴得
故 ……………………………………………………………………………………11分
也就是说存在一点满足条件. ……………12分
第8题图
第10题图
第12题图
O
同课章节目录
