11.3 角的平分线的性质自测(含答案)
文档属性
| 名称 | 11.3 角的平分线的性质自测(含答案) |
|
|
| 格式 | rar | ||
| 文件大小 | 93.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-08-29 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
11.3 角的平分线的性质自测
夯实基础
一、耐心选一选,你会开心(每题6分,共30分)
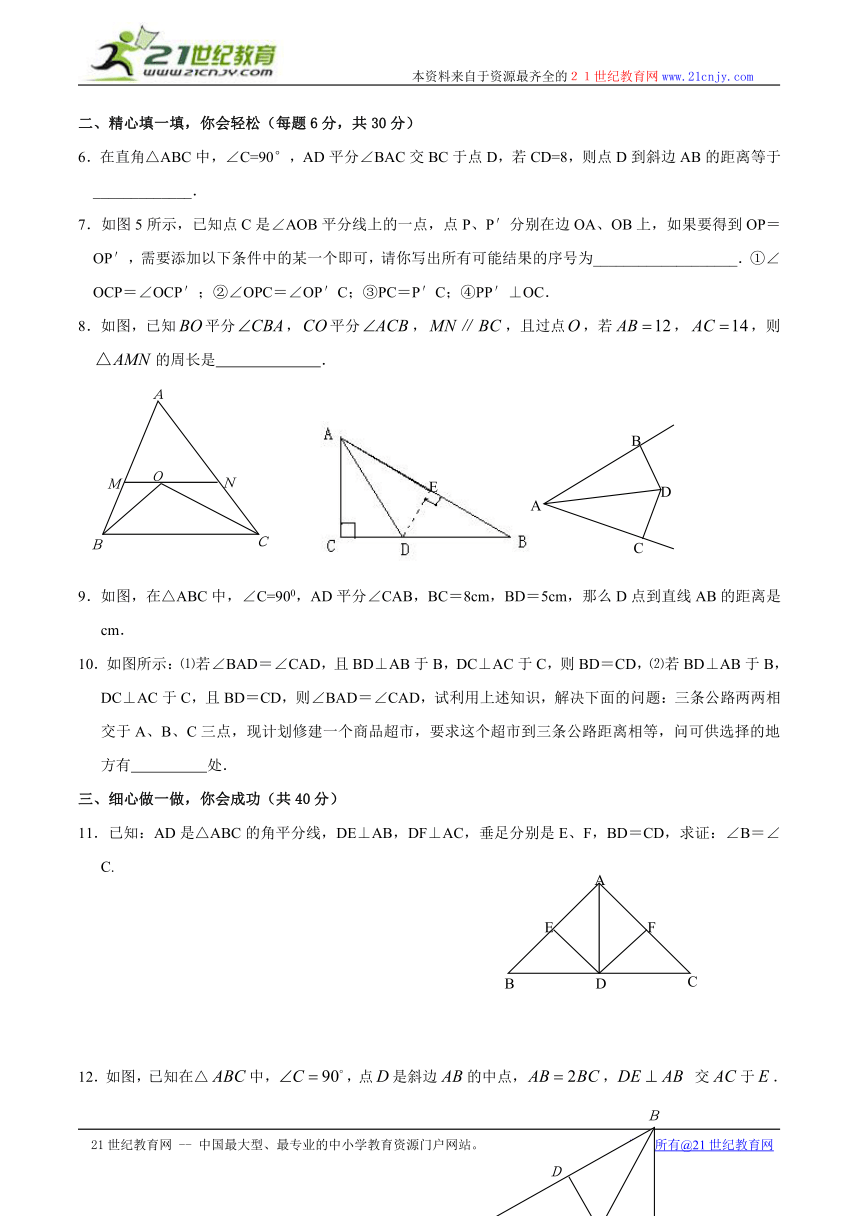
1.如图1所示,AD⊥OB,BC⊥OA,垂足分别为D、C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小是()
A.∠1=∠2 B.∠1>∠2
C.∠1<∠2 D.无法确定
2.△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=12cm,则△DBE的周长为()
A、12cm B、10cm C、14cm D、11cm
3.如图2所示,已知PA、PC分别是△ABC的外角∠DAC、∠ECA的平分线,PM⊥BD,PN⊥BE,垂足分别为M、N,那么PM与PN的关系是()
A.PM>PN B.PM=PN C.PM<PN D.无法确定
4.如图3所示,△ABC中,AB=AC,AD是∠A的平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,下面给出四个结论,其中正确的结论有( )
①AD平分∠EDF; ②AE=AF; ③AD上的点到B、C两点的距离相等
④到AE、AF距离相等的点,到DE、DF的距离也相等
A、1个 B、2个 C、3个 D、4个
5. 如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C.下列结论错误的是( ).
A.AD=CP B.△ABP≌△CBP
C.△ABD≌△CBD D.∠ADB=∠CDB.
二、精心填一填,你会轻松(每题6分,共30分)
6.在直角△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若CD=8,则点D到斜边AB的距离等于_____________.
7.如图5所示,已知点C是∠AOB平分线上的一点,点P、P′分别在边OA、OB上,如果要得到OP=OP′,需要添加以下条件中的某一个即可,请你写出所有可能结果的序号为___________________.①∠OCP=∠OCP′;②∠OPC=∠OP′C;③PC=P′C;④PP′⊥OC.
8.如图,已知平分,平分,,且过点,若,,则的周长是 .
9.如图,在△ABC中,∠C=900,AD平分∠CAB,BC=8cm,BD=5cm,那么D点到直线AB的距离是 cm.
10.如图所示:⑴若∠BAD=∠CAD,且BD⊥AB于B,DC⊥AC于C,则BD=CD,⑵若BD⊥AB于B,DC⊥AC于C,且BD=CD,则∠BAD=∠CAD,试利用上述知识,解决下面的问题:三条公路两两相交于A、B、C三点,现计划修建一个商品超市,要求这个超市到三条公路距离相等,问可供选择的地方有 处.
三、细心做一做,你会成功(共40分)
11.已知:AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,BD=CD,求证:∠B=∠C.
12.如图,已知在△中,,点是斜边的中点,, 交于.
求证:平分.
13. 先作图,再证明.
(1)在所给的图形(如图)中完成下列作图(保留作图痕迹)
①作的平分线,交于点;
②延长到点,使,连结.
(2)求证:.
综合创新
14.如图,△ABC中,P是角平分线AD,BE的交点.
求证:点P在∠C的平分线上.
15.已知:如图,,是的中点,平分.
(1)若连接,则是否平分?请你证明你的结论.
(2)线段与有怎样的位置关系?请说明理由.
中考链接
16.(2007广东茂名)的角平分 线AD交BC于 点D,,则点D到AB的距离是( )
A.1 B.2 C.3 D.4
17. (2007广东)到三角形三条边的距离都相等的点是这个三角形的( )
A.三条中线的交点 B.三条高的交点
C.三条边的垂直平分线的交点 D.三条角平分线的交点
18.(2006年镇江)⑴如图,已知△ABC,∠C=90°.按下列语句作图(尺规作图,保留作图痕迹):
①作∠B的平分线,与AC相交于点D;②在AB边上取一点E,使BE=BC ( http: / / www.1230.org )
③连接ED;⑵根据所作图形,写出一组相等的线段和一组相等的锐角.
(不包括BE=BC,∠EBD=∠CBD)
答:________________________________________________.
参考答案
夯实基础
1.选A,提示:∵AD⊥OB,BC⊥OA,PA=PB,由角平分线的判定可知∠1=∠2.
2.选A;提示:∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,易得△ACD≌△AED,∴CD=DE,AE=AC,∴△DBE的周长=DE+EB+DE=CD+DB+EB=BC+EB=AC+EB=AE+EB=AB=12cm.
3.选B,提示:过P作PT⊥AC于T,因为PA平分∠DAC,PM⊥BD,∴PM=PT,又PC平分∠ACE,PT⊥AC,PN⊥BE,∴PN=PT,∴PM=PN.
4.选D,提示:①②③④都正确.
5.A
6.8,提示:根据角平分线的性质可得D到斜边AB的距离为8.
7.①、②、④
8.26
9.由∠C=90°,AD平分∠CAB,可作DE⊥AB于E,所以D点到直线AB的距离是DE的长,由角平分线的性质可知DE=CD.又BC=8cm,BD=5cm,所以DE=CD=3cm.所以D点到直线AB的距离是3cm.
10.四处.
提示:如图2所示:⑴作出△ABC两内角的平分线,其交点为O1;⑵分别作出△ABC两外角平分线,其交点分别为O2,O3,O4,故满足条件的修建点有四处,即O1,O2,O3,O4.
11.因为AD是△ABC的角平分线,DE⊥AB,DF⊥AC,所以DE=DF,在Rt△DEB与Rt△DFC中,BD=CD,DE=DF,所以Rt△DEB≌Rt△DFC(HL),所以∠B=∠C.
12.是的中点,,
,,.
又,,,
又,(),
,平分.
13.证明:(1)作图略;
(2),,
为等腰直角三角形,.
又平分..
..
综合创新
14.如图,过点P作PM⊥AB,PN⊥BC,PQ⊥AC,垂足分别为M、N、Q.∵P在∠BAC的平分线AD上,∴PM=PQ.P在∠ABC的平分线BE上,∴PM=PN.∴PQ=PN,∴点P在∠C的平分线.
15.(1)平分.
证明:过点作,垂足为.
,,,
(角平分线上的点到角两边的距离相等).
又,.
,,
平分(到角的两边距离相等的点在这个角的平分线上).
(2),理由如下:
,
(垂直于同一条直线的两条直线平行).
(两直线平行,同旁内角互补)
又,(角平分线定义)
,,
.即.
中考链接
16.B
17.D
18.⑴作出∠B的平分线,标出交点D;标出点E,连接ED;
⑵写出DE=DC,∠BDE=∠BDC或∠ADE=∠ABC.
A
C
P
B
D
O
1
2
图1
D
M
A
B
C
N
P
E
图2
D
B
C
A
E
F
图3
A
B
C
D
P
O
A
M
B
C
N
E
B
D
C
A
A
F
C
D
E
B
B
D
A
E
C
B
A
C
A
B
C
D
E
P
2
1
3
4
D
C
M
B
A
A
C
B
A
O3
O2
O1
O4
B
C
图2
2
1
3
4
D
C
M
B
A
E
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
11.3 角的平分线的性质自测
夯实基础
一、耐心选一选,你会开心(每题6分,共30分)
1.如图1所示,AD⊥OB,BC⊥OA,垂足分别为D、C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小是()
A.∠1=∠2 B.∠1>∠2
C.∠1<∠2 D.无法确定
2.△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=12cm,则△DBE的周长为()
A、12cm B、10cm C、14cm D、11cm
3.如图2所示,已知PA、PC分别是△ABC的外角∠DAC、∠ECA的平分线,PM⊥BD,PN⊥BE,垂足分别为M、N,那么PM与PN的关系是()
A.PM>PN B.PM=PN C.PM<PN D.无法确定
4.如图3所示,△ABC中,AB=AC,AD是∠A的平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,下面给出四个结论,其中正确的结论有( )
①AD平分∠EDF; ②AE=AF; ③AD上的点到B、C两点的距离相等
④到AE、AF距离相等的点,到DE、DF的距离也相等
A、1个 B、2个 C、3个 D、4个
5. 如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C.下列结论错误的是( ).
A.AD=CP B.△ABP≌△CBP
C.△ABD≌△CBD D.∠ADB=∠CDB.
二、精心填一填,你会轻松(每题6分,共30分)
6.在直角△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若CD=8,则点D到斜边AB的距离等于_____________.
7.如图5所示,已知点C是∠AOB平分线上的一点,点P、P′分别在边OA、OB上,如果要得到OP=OP′,需要添加以下条件中的某一个即可,请你写出所有可能结果的序号为___________________.①∠OCP=∠OCP′;②∠OPC=∠OP′C;③PC=P′C;④PP′⊥OC.
8.如图,已知平分,平分,,且过点,若,,则的周长是 .
9.如图,在△ABC中,∠C=900,AD平分∠CAB,BC=8cm,BD=5cm,那么D点到直线AB的距离是 cm.
10.如图所示:⑴若∠BAD=∠CAD,且BD⊥AB于B,DC⊥AC于C,则BD=CD,⑵若BD⊥AB于B,DC⊥AC于C,且BD=CD,则∠BAD=∠CAD,试利用上述知识,解决下面的问题:三条公路两两相交于A、B、C三点,现计划修建一个商品超市,要求这个超市到三条公路距离相等,问可供选择的地方有 处.
三、细心做一做,你会成功(共40分)
11.已知:AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,BD=CD,求证:∠B=∠C.
12.如图,已知在△中,,点是斜边的中点,, 交于.
求证:平分.
13. 先作图,再证明.
(1)在所给的图形(如图)中完成下列作图(保留作图痕迹)
①作的平分线,交于点;
②延长到点,使,连结.
(2)求证:.
综合创新
14.如图,△ABC中,P是角平分线AD,BE的交点.
求证:点P在∠C的平分线上.
15.已知:如图,,是的中点,平分.
(1)若连接,则是否平分?请你证明你的结论.
(2)线段与有怎样的位置关系?请说明理由.
中考链接
16.(2007广东茂名)的角平分 线AD交BC于 点D,,则点D到AB的距离是( )
A.1 B.2 C.3 D.4
17. (2007广东)到三角形三条边的距离都相等的点是这个三角形的( )
A.三条中线的交点 B.三条高的交点
C.三条边的垂直平分线的交点 D.三条角平分线的交点
18.(2006年镇江)⑴如图,已知△ABC,∠C=90°.按下列语句作图(尺规作图,保留作图痕迹):
①作∠B的平分线,与AC相交于点D;②在AB边上取一点E,使BE=BC ( http: / / www.1230.org )
③连接ED;⑵根据所作图形,写出一组相等的线段和一组相等的锐角.
(不包括BE=BC,∠EBD=∠CBD)
答:________________________________________________.
参考答案
夯实基础
1.选A,提示:∵AD⊥OB,BC⊥OA,PA=PB,由角平分线的判定可知∠1=∠2.
2.选A;提示:∵AD是∠BAC的平分线,DE⊥AB,∠C=90°,易得△ACD≌△AED,∴CD=DE,AE=AC,∴△DBE的周长=DE+EB+DE=CD+DB+EB=BC+EB=AC+EB=AE+EB=AB=12cm.
3.选B,提示:过P作PT⊥AC于T,因为PA平分∠DAC,PM⊥BD,∴PM=PT,又PC平分∠ACE,PT⊥AC,PN⊥BE,∴PN=PT,∴PM=PN.
4.选D,提示:①②③④都正确.
5.A
6.8,提示:根据角平分线的性质可得D到斜边AB的距离为8.
7.①、②、④
8.26
9.由∠C=90°,AD平分∠CAB,可作DE⊥AB于E,所以D点到直线AB的距离是DE的长,由角平分线的性质可知DE=CD.又BC=8cm,BD=5cm,所以DE=CD=3cm.所以D点到直线AB的距离是3cm.
10.四处.
提示:如图2所示:⑴作出△ABC两内角的平分线,其交点为O1;⑵分别作出△ABC两外角平分线,其交点分别为O2,O3,O4,故满足条件的修建点有四处,即O1,O2,O3,O4.
11.因为AD是△ABC的角平分线,DE⊥AB,DF⊥AC,所以DE=DF,在Rt△DEB与Rt△DFC中,BD=CD,DE=DF,所以Rt△DEB≌Rt△DFC(HL),所以∠B=∠C.
12.是的中点,,
,,.
又,,,
又,(),
,平分.
13.证明:(1)作图略;
(2),,
为等腰直角三角形,.
又平分..
..
综合创新
14.如图,过点P作PM⊥AB,PN⊥BC,PQ⊥AC,垂足分别为M、N、Q.∵P在∠BAC的平分线AD上,∴PM=PQ.P在∠ABC的平分线BE上,∴PM=PN.∴PQ=PN,∴点P在∠C的平分线.
15.(1)平分.
证明:过点作,垂足为.
,,,
(角平分线上的点到角两边的距离相等).
又,.
,,
平分(到角的两边距离相等的点在这个角的平分线上).
(2),理由如下:
,
(垂直于同一条直线的两条直线平行).
(两直线平行,同旁内角互补)
又,(角平分线定义)
,,
.即.
中考链接
16.B
17.D
18.⑴作出∠B的平分线,标出交点D;标出点E,连接ED;
⑵写出DE=DC,∠BDE=∠BDC或∠ADE=∠ABC.
A
C
P
B
D
O
1
2
图1
D
M
A
B
C
N
P
E
图2
D
B
C
A
E
F
图3
A
B
C
D
P
O
A
M
B
C
N
E
B
D
C
A
A
F
C
D
E
B
B
D
A
E
C
B
A
C
A
B
C
D
E
P
2
1
3
4
D
C
M
B
A
A
C
B
A
O3
O2
O1
O4
B
C
图2
2
1
3
4
D
C
M
B
A
E
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
