数学人教A版(2019)必修第一册5.2.1三角函数的概念(共23张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.2.1三角函数的概念(共23张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 18:43:35 | ||
图片预览





文档简介
(共23张PPT)
5.2.1 三角函数的概念
阅读引言
现实世界中的许多运动、变化都有着循环往复、周而复始的规律,这种变化规律称为周期性。例如:地球自转引起的昼夜交替变化和公转引起的四季交替变化,月亮圆缺,潮汐变化,物体做匀速圆周运动时的位置变化,物体做简谐运动时的位移变化,交变电流变化等。这些现象都可以用三角函数刻画。
一、创设情境
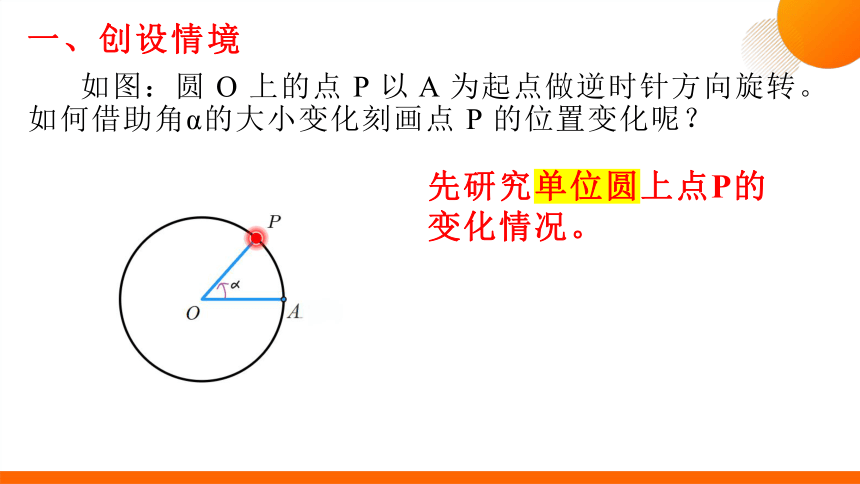
如图:圆 O 上的点 P 以 A 为起点做逆时针方向旋转。如何借助角α的大小变化刻画点 P 的位置变化呢?
先研究单位圆上点P的变化情况。
一、创设情境
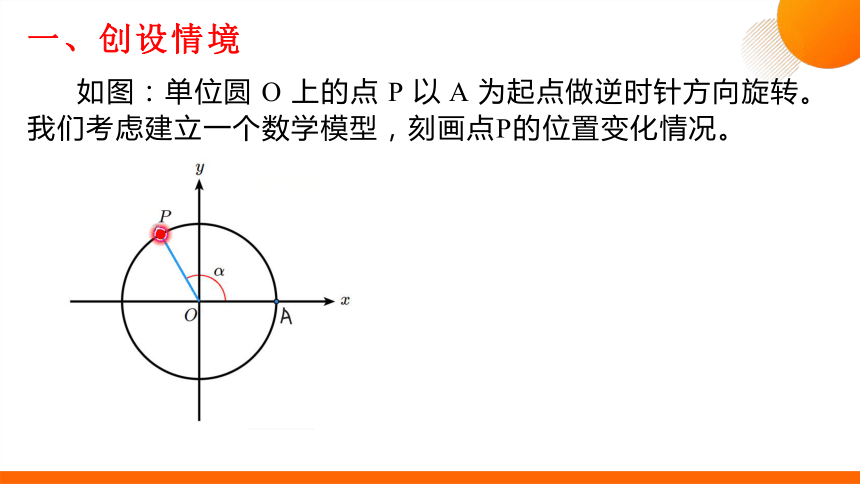
如图:单位圆 O 上的点 P 以 A 为起点做逆时针方向旋转。我们考虑建立一个数学模型,刻画点P的位置变化情况。
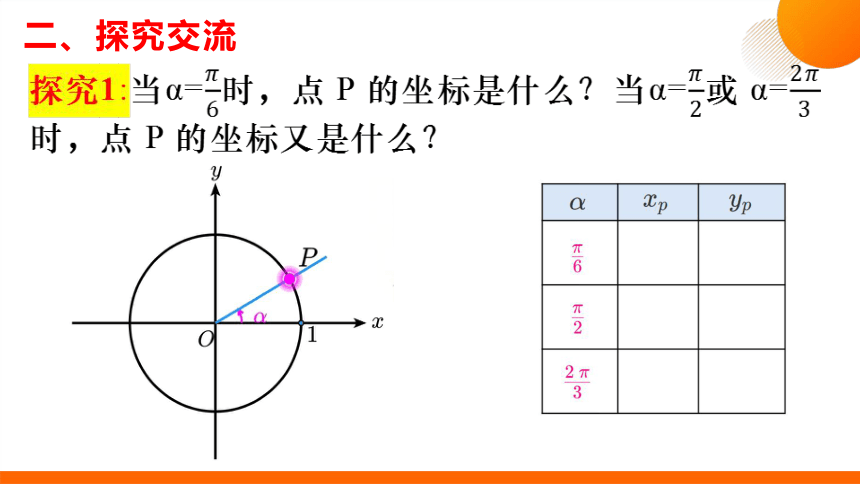
探究1:当α=时,点 P 的坐标是什么?当α=或 α=时,点 P 的坐标又是什么?
二、探究交流
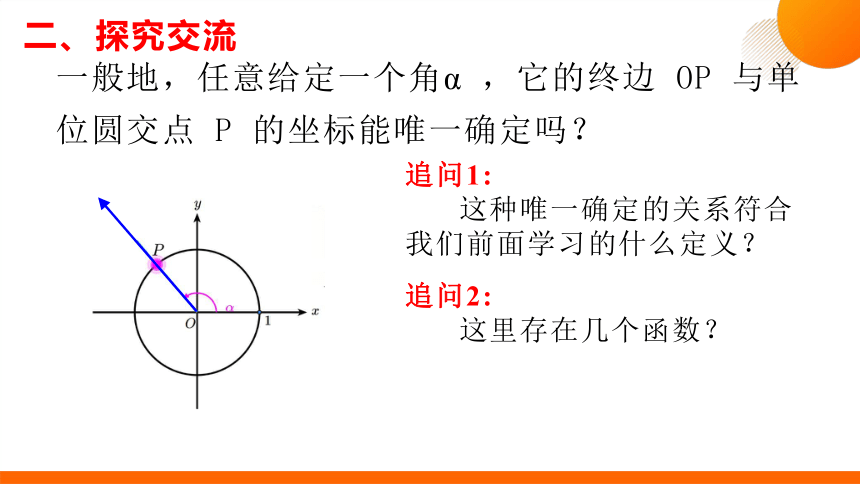
一般地,任意给定一个角α ,它的终边 OP 与单位圆交点 P 的坐标能唯一确定吗?
追问1:
这种唯一确定的关系符合我们前面学习的什么定义?
二、探究交流
追问2:
这里存在几个函数?
三、抽象定义
定义:设 α 是一个任意角, αR ,它的终边 OP 与单位圆相交于点 P ( x , y ).
把点 P 的纵坐标 y 叫做α 的正弦函数,记作 sinα ,即y = sinα ;
把点 P 的横坐标 x 叫做α 的余弦函数,记作 cos α ,即 x = cosα ;
把比值叫做α的正切,记作 tanα 。
定义:设 α 是一个任意角, αR ,它的终边 OP 与单位圆相交于点 P ( x , y ).
(1)把点 P 的纵坐标 y 叫做 α 的正弦函数,记作 sinα ,即
y = sinα ;
(2)把点 P 的横坐标 x 叫做α 的余弦函数,记作 cos α ,即
x = cosα ;
(3)把点 P 的纵坐标与横坐标的比值叫做α的正切函数,记作 tanα ,即 = tan α ( x ≠0).
三、抽象定义
三、抽象定义
我们将正弦函数、余弦函数和正切函数统称为三角函数,通常将它们记为:
正弦函数
余弦函数
正切函数
思考:在初中我们学习的锐角三角函数是如何定义的?两种定义有什么区别和联系?
锐角三角函数
任意角三角函数
四、新旧知识的联系
四、新旧知识的联系
探究2:设 α(0,),把按锐角三角函数定义求得的 α的正弦记为z1,把按本节三角函数定义求得的锐角 α的正弦记为 y1 , y1 与z1相等吗?对于余弦、正切也有相同的结论吗?
四、新旧知识的联系
探究2:设 α(0,),把按锐角三角函数定义求得的 α的正弦记为z1,把按本节三角函数定义求得的锐角 α的正弦记为 y1 , y1 与z1相等吗?对于余弦、正切也有相同的结论吗?
四、新旧知识的联系
探究2:设 α(0,),把按锐角三角函数定义求得的 α的正弦记为z1,把按本节三角函数定义求得的锐角 α的正弦记为 y1 , y1 与z1相等吗?对于余弦、正切也有相同的结论吗?
概念举例 说出α=,,的正弦值、余弦值、正切值。
例1.求的正弦、余弦和正切值.
解:在直角坐标系中,作易知的终边与单位圆的交点坐标为.所以有:
例1.求的正弦、余弦和正切值.
2.求的正弦、余弦和正切值.
课本P180 练习2
例2.如图,设是一个任意角,它的终边上任意一点(不与原点重合)的坐标为,点与原点的距离为.
求证:
证明:如图,设角的终边与单位圆交于交点分别过点,作轴的垂线,垂足分别为则:
,,,,
于是,,即.因为与同号,所以即同理可得,
例2.如图,设是一个任意角,它的终边上任意一点(不与原点重合)的坐标为,点与原点的距离为.
求证:
课本P180 练习3
3.已知角的终边过点P(-12,5),求角的三角函数值。
变式:已知角α的终边过点P(-12a,5a)(a≠0),求角α的三角函数值。
课本P180 练习4
4.已知点P在半径为2的圆上按顺时针方向做匀速圆周运动,角速度为1rad/s,求2s时点P所在的位置。
课堂小结
感谢聆听!
5.2.1 三角函数的概念
阅读引言
现实世界中的许多运动、变化都有着循环往复、周而复始的规律,这种变化规律称为周期性。例如:地球自转引起的昼夜交替变化和公转引起的四季交替变化,月亮圆缺,潮汐变化,物体做匀速圆周运动时的位置变化,物体做简谐运动时的位移变化,交变电流变化等。这些现象都可以用三角函数刻画。
一、创设情境
如图:圆 O 上的点 P 以 A 为起点做逆时针方向旋转。如何借助角α的大小变化刻画点 P 的位置变化呢?
先研究单位圆上点P的变化情况。
一、创设情境
如图:单位圆 O 上的点 P 以 A 为起点做逆时针方向旋转。我们考虑建立一个数学模型,刻画点P的位置变化情况。
探究1:当α=时,点 P 的坐标是什么?当α=或 α=时,点 P 的坐标又是什么?
二、探究交流
一般地,任意给定一个角α ,它的终边 OP 与单位圆交点 P 的坐标能唯一确定吗?
追问1:
这种唯一确定的关系符合我们前面学习的什么定义?
二、探究交流
追问2:
这里存在几个函数?
三、抽象定义
定义:设 α 是一个任意角, αR ,它的终边 OP 与单位圆相交于点 P ( x , y ).
把点 P 的纵坐标 y 叫做α 的正弦函数,记作 sinα ,即y = sinα ;
把点 P 的横坐标 x 叫做α 的余弦函数,记作 cos α ,即 x = cosα ;
把比值叫做α的正切,记作 tanα 。
定义:设 α 是一个任意角, αR ,它的终边 OP 与单位圆相交于点 P ( x , y ).
(1)把点 P 的纵坐标 y 叫做 α 的正弦函数,记作 sinα ,即
y = sinα ;
(2)把点 P 的横坐标 x 叫做α 的余弦函数,记作 cos α ,即
x = cosα ;
(3)把点 P 的纵坐标与横坐标的比值叫做α的正切函数,记作 tanα ,即 = tan α ( x ≠0).
三、抽象定义
三、抽象定义
我们将正弦函数、余弦函数和正切函数统称为三角函数,通常将它们记为:
正弦函数
余弦函数
正切函数
思考:在初中我们学习的锐角三角函数是如何定义的?两种定义有什么区别和联系?
锐角三角函数
任意角三角函数
四、新旧知识的联系
四、新旧知识的联系
探究2:设 α(0,),把按锐角三角函数定义求得的 α的正弦记为z1,把按本节三角函数定义求得的锐角 α的正弦记为 y1 , y1 与z1相等吗?对于余弦、正切也有相同的结论吗?
四、新旧知识的联系
探究2:设 α(0,),把按锐角三角函数定义求得的 α的正弦记为z1,把按本节三角函数定义求得的锐角 α的正弦记为 y1 , y1 与z1相等吗?对于余弦、正切也有相同的结论吗?
四、新旧知识的联系
探究2:设 α(0,),把按锐角三角函数定义求得的 α的正弦记为z1,把按本节三角函数定义求得的锐角 α的正弦记为 y1 , y1 与z1相等吗?对于余弦、正切也有相同的结论吗?
概念举例 说出α=,,的正弦值、余弦值、正切值。
例1.求的正弦、余弦和正切值.
解:在直角坐标系中,作易知的终边与单位圆的交点坐标为.所以有:
例1.求的正弦、余弦和正切值.
2.求的正弦、余弦和正切值.
课本P180 练习2
例2.如图,设是一个任意角,它的终边上任意一点(不与原点重合)的坐标为,点与原点的距离为.
求证:
证明:如图,设角的终边与单位圆交于交点分别过点,作轴的垂线,垂足分别为则:
,,,,
于是,,即.因为与同号,所以即同理可得,
例2.如图,设是一个任意角,它的终边上任意一点(不与原点重合)的坐标为,点与原点的距离为.
求证:
课本P180 练习3
3.已知角的终边过点P(-12,5),求角的三角函数值。
变式:已知角α的终边过点P(-12a,5a)(a≠0),求角α的三角函数值。
课本P180 练习4
4.已知点P在半径为2的圆上按顺时针方向做匀速圆周运动,角速度为1rad/s,求2s时点P所在的位置。
课堂小结
感谢聆听!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
