18.2.1矩形课件
图片预览




文档简介
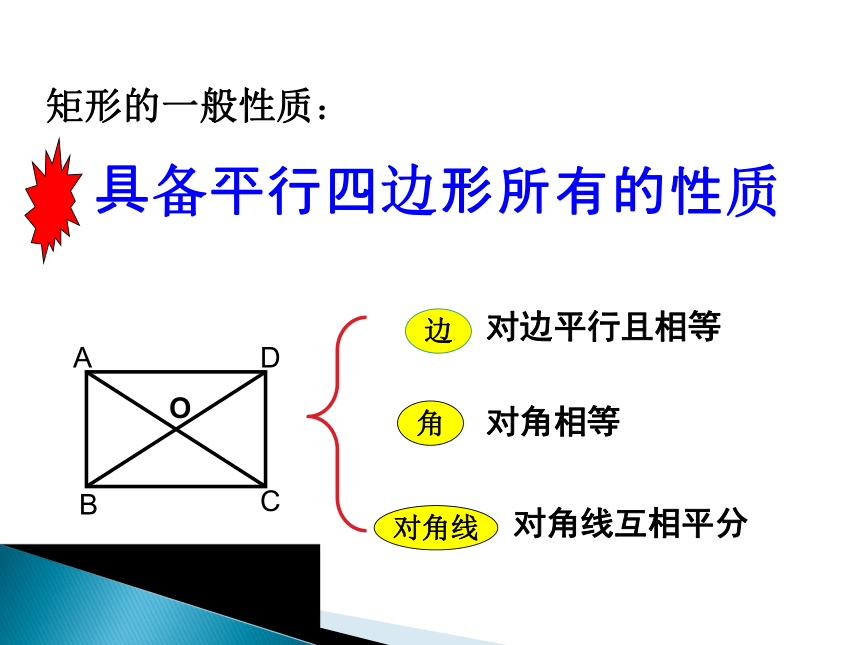
课件43张PPT。18.2 特殊的平行四边形18.2.1 矩形有一个角是直角的平行四边形是矩形矩形的定义:对边平行且相等对角相等对角线互相平分矩形的一般性质:探索新知:
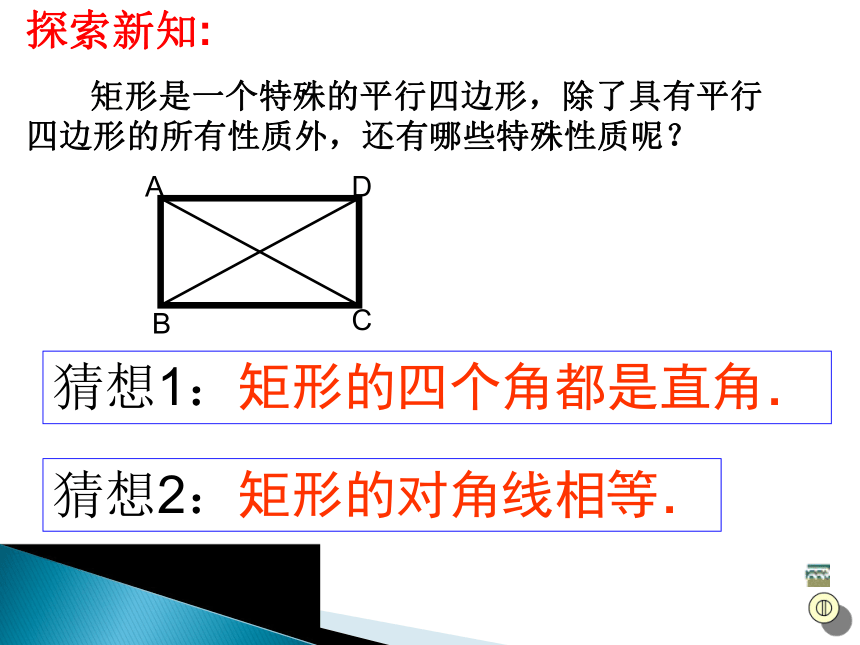
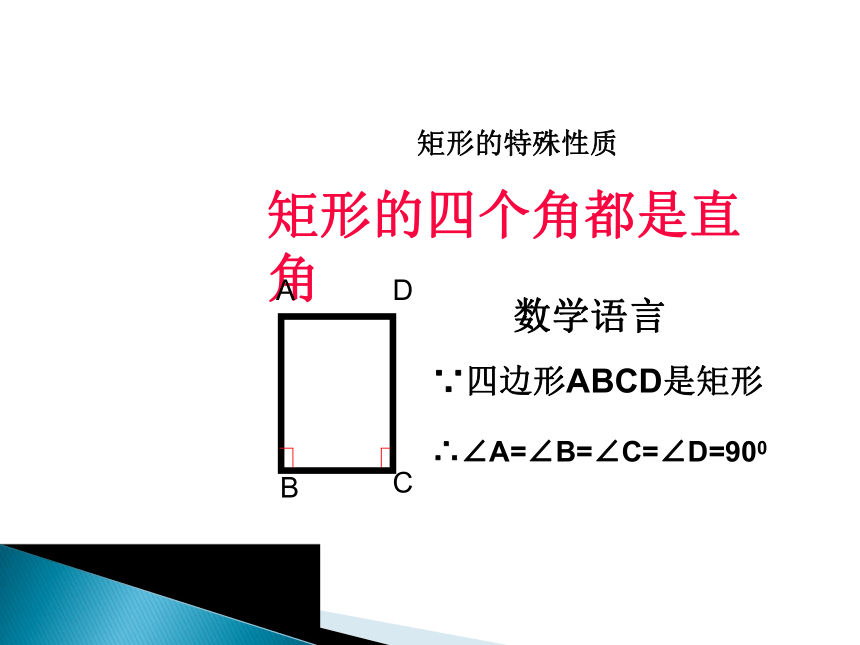
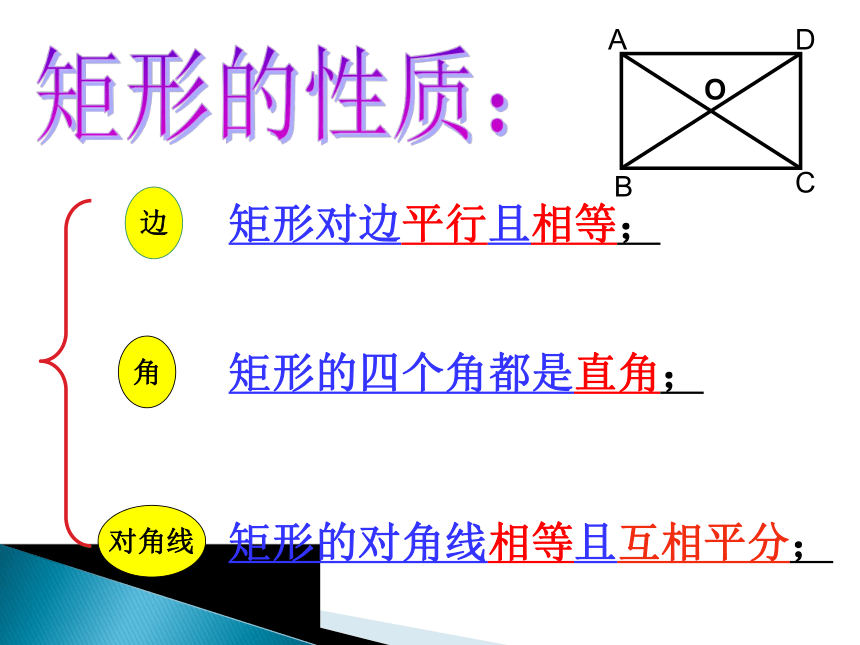
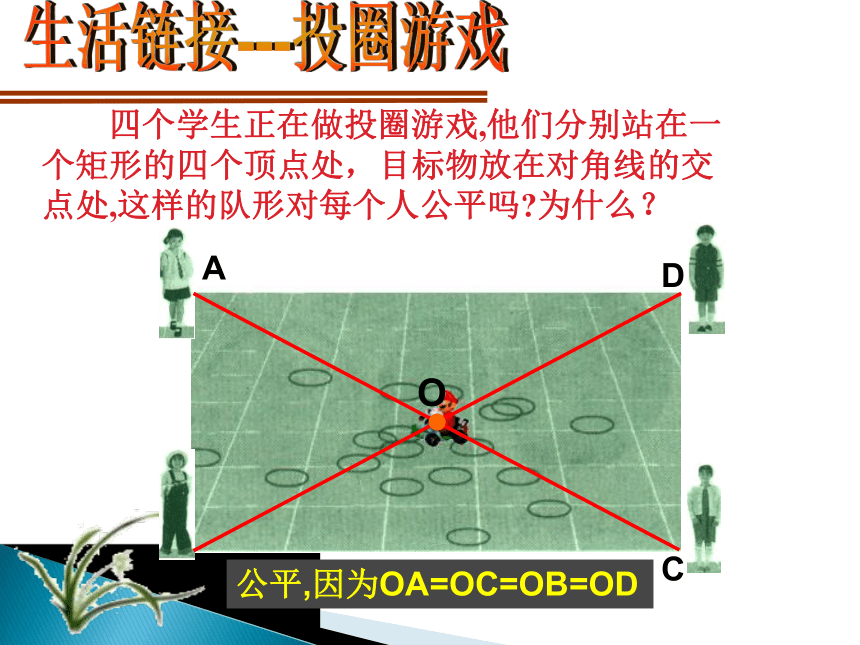
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.ABCD矩形特殊的性质矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:矩形的特殊性质矩形的四个角都是直角数学语言∵四边形ABCD是矩形 ∴∠A=∠B=∠C=∠D=900矩形的特殊性质矩形的对角线相等数学语言∵四边形ABCD是矩形 ∴AC = BD边对角线角矩形的性质:矩形对边平行且相等;矩形的四个角都是直角;矩形的对角线相等且互相平分;OABCD公平,因为OA=OC=OB=OD生活链接---投圈游戏ABCO得到:直角三角形的一个性质
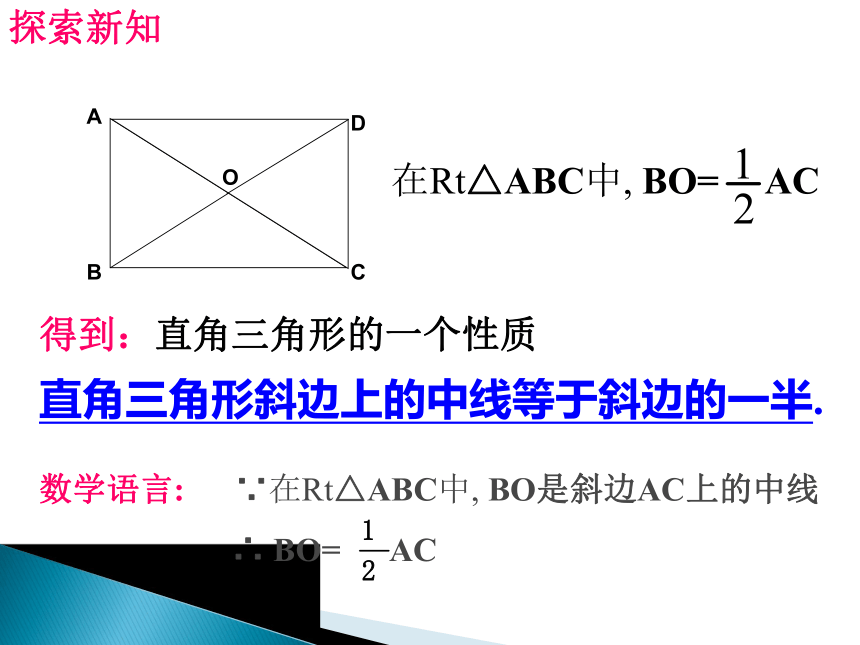
直角三角形斜边上的中线等于斜边的一半.数学语言: ∵在Rt△ABC中, BO是斜边AC上的中线
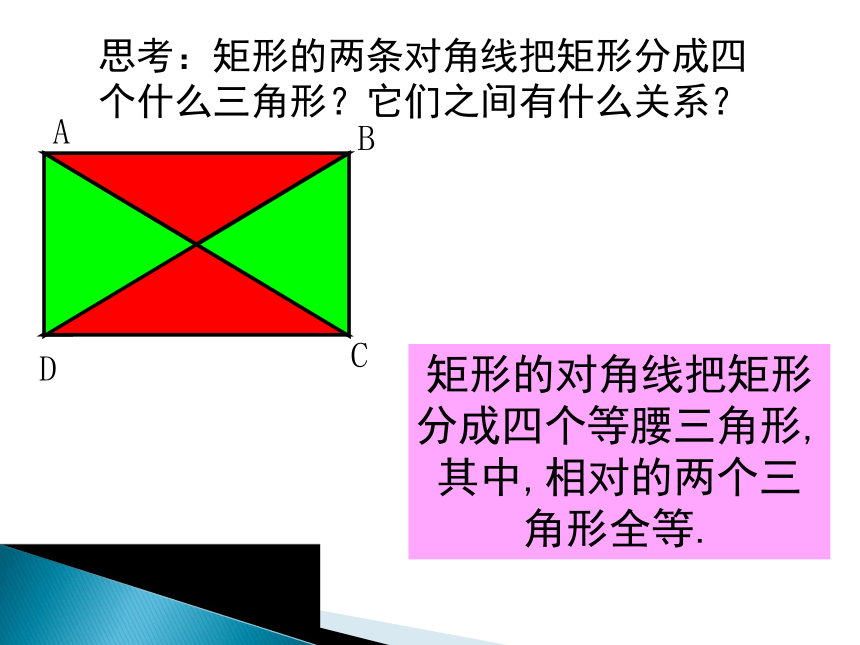
∴ BO= AC在Rt△ABC中, BO= AC探索新知ABCDO矩形的对角线把矩形分成四个等腰三角形,其中,相对的两个三角形全等.思考:矩形的两条对角线把矩形分成四个什么三角形?它们之间有什么关系? 1.矩形具有而一般平行四边形不具有的性质是( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分2.下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等
C.是轴对称图形 D.对角线互相垂直AD练习1:3、如图,在矩形ABCD中,AC与BD相交于点O,AB=3cm,BC=4cm 则AC= cm,BO= cm,
矩形的周长为 cm,
矩形的面积为 cm252.5 练习1:1412矩形的两条边和对角线构成一个 三角形, 是斜边.
求矩形的边长和对角线的问题可转化为直角三角形,利用 解决.直角对角线勾股定理快速回答
1、已知矩形的两边长分别为8和6,则矩形的对角线长为 .
2、已知矩形的对角线长为3cm,一边长为2cm,则另一边长为 .10例: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?方法小结: 如果矩形两对角 线的夹角是60°
或120°, 则其中必有等边三角形. ∴AC与BD相等且互相平分∴ OA=OB∵ ∠AOB=60°∴ △AOB是等边三角形∴ OA=AB=4(㎝)∴ 矩形的对角线长 AC=BD=2OA=8(㎝)解:∵ 四边形ABCD是矩形练习:教材104页练习1 如图,在矩形ABCD中,找出相等的线段与相等的角。小试牛刀成长快乐训练营点击进入 矩形具有而一般平行四边形不
具有的性质是 ( ) B.对边相等C营中热身已知:四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
2.若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm
AB= _____cm5104营中寻宝4.已知△ABC是Rt△,∠ABC=900,
BD是斜边AC上的中线(1)若BD=3㎝ 则AC= ㎝
(2) 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝.6510营中寻宝本课小结矩形的四个角都是直角.※ 矩形的性质定理1矩形的对角线相等.※ 矩形的性质定理2※ 直角三角形的一个性质 直角三角形斜边上的中线等于斜边的一半.反思拓展:1、工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图1),使
AB=CD, EF=GH;
(2)摆放成如图(2)的四边形,则这时窗框的形状是
_____,根据的数学道理是__________;
(3)将直角尺靠紧窗框的一个角(如图3)调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图4),说明窗框合格,这时窗框是____,根据的数学道理是________________。平行四边形两组对边分别相等的四边形是平行四边形矩形有一个角是直角的平行四边形是矩形1.练习第3题
2. 习题18.2 第1; 2; 4 。
课后作业:求证:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形求证:∠A=∠B=∠C=∠D=90°证明: ∵四边形ABCD是矩形∴ ∠A=90°又 矩形ABCD是平行四边形∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 90°∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角已知:如图,四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD 即矩形的对角线相等求证:矩形的对角线相等请多多指教!☆ 矩 形 的 判 定 ☆定义:有一个角是直角的平行四边形叫做矩形推论:直角三角形斜边上的中线等于斜边的一半∵∠ACB=90°AD = BD
∴CD = AB复习与回顾矩形的判定定义:有一个角是直角的平行四边形叫做矩形判定定理1 有三个角是直角的四边形是矩形判定定理2 对角线相等的平行四边形是矩形例如:∠A= ∠B= ∠C=90°四边形ABCD是矩形例如:例1
练习
小结判定定理1 有三个角是直角的四边形是矩形证明:∵ ∠A= ∠B= ∠C=90°
∴ ∠A + ∠B = 180°
∠B + ∠C = 180°
∴AD∥BC, AB∥DC
∴四边形ABCD是平行四边形
∵ ∠A=90°
∴四边形ABCD是矩形判定定理2 对角线相等的平行四边形是矩形例1 已知 ABCD的对角线AC、BD交于O,△AOB是
等边三角形,AB = 4cm,求这个平行四边形的面积.1. 对角线相等且一组对边也相等的四边形是矩形.
2. 两条对角线交点到四个顶点距离相等的四边形为矩形.
3. 有一组对边相等,一组对角是直角的四边形是矩形.
4. 有三个角都相等的四边形是矩形. 5. 具备条件____的四边形是矩形. A.两条对角线相等 B.对角线互相垂直
C.一组对角是直角 D.有三个角是直角 6. 能够判断一个四边形是矩形的条件是 A.对角线相等 B.对角线垂直
C.对角线互相平分且相等 D.对角线垂直且相等
判断题选择题( )( )( )( )[ ][ ]课堂练习×√√×CD如图,在平行四边形ABCD中,AC与BD 交于O,如图,
①若∠1=∠2,则平行四边形
ABCD是矩形吗?为什么?
②若△AOB是正三角形,
则平行四边形ABCD是矩形
是矩形吗?为什么?
巩固练习ADBCO)12(
∟∟∟ABCD命题:有三个角是直角的四边形是矩形证明:∵四边形中有三个角是直角
四边形的内角和为360O
∴第四个角也是直角
∴两组对角分别相等且每个角都是直角
∴这个四边形是矩形
按步骤画“边-直角,边-直角,边-直角,边”这样四步画出一个四边形,判断这个四边形是一个矩形吗?说明理由。
判断下列说法是否正确:
对角线相等的四边形是矩形. ( )
对角线互相平分且相等的四边形是矩形.( )
有一个角是直角的四边形是矩形. ( )
四个角都相等的四边形是矩形.( )
对角线相等且互相垂直的四边形是矩形. ( )
议一议:× √ × √ ×某车间生产矩形工件,如图,若你是质检员:
身边只有直尺,你该如何检验它是否合格。
身边只有直角尺,你该如何检验它是否合格。例题练一练(一)下列各句判定矩形的说法是否正确?为什么?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(4)有四个角是直角的四边形是矩形;
(5)四个角都相等的四边形是矩形;
(6)对角线相等,且有一个角是直角的四边形是矩形;
(7)一组邻边垂直,一组对边平行且相等的四边形是矩形;
(8)对角线相等且互相垂直的四边形是矩形.×√√√√×××(l)所给四边形添加的条件不满足三个的肯定不是矩形;
(2)所给四边形添加的条件是三个独立条件,但若与定
理不同,则需要利用定义和判定定理证明或举反例,
才能下结论.练一练(二)1.已知:矩形ABCD的两条对角线相交于点O,
∠AOD= 120°,AB=4cm.求矩形对角线的长.2.已知平行四边形ABCD的对角线AC和BD相交于
点O,△AOB是等边三角形,AB= 4 cm.求这
个平行四边形的面积.练一练(三)1.已知:四边形ABCD为矩形,PB=PC,求证:PA=PD
2.已知:如图,在平行四边形ABCD中,M为BC中点.
∠MAD=∠MDA.求证:四边形 ABCD是矩形.
MN练一练(三)3.已知:如图,平行四边形ABCD的四个内角平分线相
交于点E,F, G,H.求证:EG=FH.4.已知:如图,在△ABC中,∠C= 90°,CD为中线,
延长CD到点E,使得 DE=CD.连结AE,BE,
则四边形ACBE为矩形.
小 结:矩形的判定方法分两类:
从四边形来判定和从平行四边形来判定.常用的判定方法有三种:
定义和两个判定定理.遇到具体题目,
可根据条件灵活选用恰当的方法.提示:判定一个四边形是矩形,应先认清是任
意四边形,还是平行四边形,然后选择适
当的方法判定。
小结:平行四边形的判定有一个角是直角的平行四边形对角线相等的平行四边形有三个角是直角对角线互相平分且相等
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.ABCD矩形特殊的性质矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:矩形的特殊性质矩形的四个角都是直角数学语言∵四边形ABCD是矩形 ∴∠A=∠B=∠C=∠D=900矩形的特殊性质矩形的对角线相等数学语言∵四边形ABCD是矩形 ∴AC = BD边对角线角矩形的性质:矩形对边平行且相等;矩形的四个角都是直角;矩形的对角线相等且互相平分;OABCD公平,因为OA=OC=OB=OD生活链接---投圈游戏ABCO得到:直角三角形的一个性质
直角三角形斜边上的中线等于斜边的一半.数学语言: ∵在Rt△ABC中, BO是斜边AC上的中线
∴ BO= AC在Rt△ABC中, BO= AC探索新知ABCDO矩形的对角线把矩形分成四个等腰三角形,其中,相对的两个三角形全等.思考:矩形的两条对角线把矩形分成四个什么三角形?它们之间有什么关系? 1.矩形具有而一般平行四边形不具有的性质是( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分2.下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等
C.是轴对称图形 D.对角线互相垂直AD练习1:3、如图,在矩形ABCD中,AC与BD相交于点O,AB=3cm,BC=4cm 则AC= cm,BO= cm,
矩形的周长为 cm,
矩形的面积为 cm252.5 练习1:1412矩形的两条边和对角线构成一个 三角形, 是斜边.
求矩形的边长和对角线的问题可转化为直角三角形,利用 解决.直角对角线勾股定理快速回答
1、已知矩形的两边长分别为8和6,则矩形的对角线长为 .
2、已知矩形的对角线长为3cm,一边长为2cm,则另一边长为 .10例: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?方法小结: 如果矩形两对角 线的夹角是60°
或120°, 则其中必有等边三角形. ∴AC与BD相等且互相平分∴ OA=OB∵ ∠AOB=60°∴ △AOB是等边三角形∴ OA=AB=4(㎝)∴ 矩形的对角线长 AC=BD=2OA=8(㎝)解:∵ 四边形ABCD是矩形练习:教材104页练习1 如图,在矩形ABCD中,找出相等的线段与相等的角。小试牛刀成长快乐训练营点击进入 矩形具有而一般平行四边形不
具有的性质是 ( ) B.对边相等C营中热身已知:四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ OB=_______ ㎝
2.若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm
AB= _____cm5104营中寻宝4.已知△ABC是Rt△,∠ABC=900,
BD是斜边AC上的中线(1)若BD=3㎝ 则AC= ㎝
(2) 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝.6510营中寻宝本课小结矩形的四个角都是直角.※ 矩形的性质定理1矩形的对角线相等.※ 矩形的性质定理2※ 直角三角形的一个性质 直角三角形斜边上的中线等于斜边的一半.反思拓展:1、工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图1),使
AB=CD, EF=GH;
(2)摆放成如图(2)的四边形,则这时窗框的形状是
_____,根据的数学道理是__________;
(3)将直角尺靠紧窗框的一个角(如图3)调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图4),说明窗框合格,这时窗框是____,根据的数学道理是________________。平行四边形两组对边分别相等的四边形是平行四边形矩形有一个角是直角的平行四边形是矩形1.练习第3题
2. 习题18.2 第1; 2; 4 。
课后作业:求证:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形求证:∠A=∠B=∠C=∠D=90°证明: ∵四边形ABCD是矩形∴ ∠A=90°又 矩形ABCD是平行四边形∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 90°∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角已知:如图,四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD 即矩形的对角线相等求证:矩形的对角线相等请多多指教!☆ 矩 形 的 判 定 ☆定义:有一个角是直角的平行四边形叫做矩形推论:直角三角形斜边上的中线等于斜边的一半∵∠ACB=90°AD = BD
∴CD = AB复习与回顾矩形的判定定义:有一个角是直角的平行四边形叫做矩形判定定理1 有三个角是直角的四边形是矩形判定定理2 对角线相等的平行四边形是矩形例如:∠A= ∠B= ∠C=90°四边形ABCD是矩形例如:例1
练习
小结判定定理1 有三个角是直角的四边形是矩形证明:∵ ∠A= ∠B= ∠C=90°
∴ ∠A + ∠B = 180°
∠B + ∠C = 180°
∴AD∥BC, AB∥DC
∴四边形ABCD是平行四边形
∵ ∠A=90°
∴四边形ABCD是矩形判定定理2 对角线相等的平行四边形是矩形例1 已知 ABCD的对角线AC、BD交于O,△AOB是
等边三角形,AB = 4cm,求这个平行四边形的面积.1. 对角线相等且一组对边也相等的四边形是矩形.
2. 两条对角线交点到四个顶点距离相等的四边形为矩形.
3. 有一组对边相等,一组对角是直角的四边形是矩形.
4. 有三个角都相等的四边形是矩形. 5. 具备条件____的四边形是矩形. A.两条对角线相等 B.对角线互相垂直
C.一组对角是直角 D.有三个角是直角 6. 能够判断一个四边形是矩形的条件是 A.对角线相等 B.对角线垂直
C.对角线互相平分且相等 D.对角线垂直且相等
判断题选择题( )( )( )( )[ ][ ]课堂练习×√√×CD如图,在平行四边形ABCD中,AC与BD 交于O,如图,
①若∠1=∠2,则平行四边形
ABCD是矩形吗?为什么?
②若△AOB是正三角形,
则平行四边形ABCD是矩形
是矩形吗?为什么?
巩固练习ADBCO)12(
∟∟∟ABCD命题:有三个角是直角的四边形是矩形证明:∵四边形中有三个角是直角
四边形的内角和为360O
∴第四个角也是直角
∴两组对角分别相等且每个角都是直角
∴这个四边形是矩形
按步骤画“边-直角,边-直角,边-直角,边”这样四步画出一个四边形,判断这个四边形是一个矩形吗?说明理由。
判断下列说法是否正确:
对角线相等的四边形是矩形. ( )
对角线互相平分且相等的四边形是矩形.( )
有一个角是直角的四边形是矩形. ( )
四个角都相等的四边形是矩形.( )
对角线相等且互相垂直的四边形是矩形. ( )
议一议:× √ × √ ×某车间生产矩形工件,如图,若你是质检员:
身边只有直尺,你该如何检验它是否合格。
身边只有直角尺,你该如何检验它是否合格。例题练一练(一)下列各句判定矩形的说法是否正确?为什么?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(4)有四个角是直角的四边形是矩形;
(5)四个角都相等的四边形是矩形;
(6)对角线相等,且有一个角是直角的四边形是矩形;
(7)一组邻边垂直,一组对边平行且相等的四边形是矩形;
(8)对角线相等且互相垂直的四边形是矩形.×√√√√×××(l)所给四边形添加的条件不满足三个的肯定不是矩形;
(2)所给四边形添加的条件是三个独立条件,但若与定
理不同,则需要利用定义和判定定理证明或举反例,
才能下结论.练一练(二)1.已知:矩形ABCD的两条对角线相交于点O,
∠AOD= 120°,AB=4cm.求矩形对角线的长.2.已知平行四边形ABCD的对角线AC和BD相交于
点O,△AOB是等边三角形,AB= 4 cm.求这
个平行四边形的面积.练一练(三)1.已知:四边形ABCD为矩形,PB=PC,求证:PA=PD
2.已知:如图,在平行四边形ABCD中,M为BC中点.
∠MAD=∠MDA.求证:四边形 ABCD是矩形.
MN练一练(三)3.已知:如图,平行四边形ABCD的四个内角平分线相
交于点E,F, G,H.求证:EG=FH.4.已知:如图,在△ABC中,∠C= 90°,CD为中线,
延长CD到点E,使得 DE=CD.连结AE,BE,
则四边形ACBE为矩形.
小 结:矩形的判定方法分两类:
从四边形来判定和从平行四边形来判定.常用的判定方法有三种:
定义和两个判定定理.遇到具体题目,
可根据条件灵活选用恰当的方法.提示:判定一个四边形是矩形,应先认清是任
意四边形,还是平行四边形,然后选择适
当的方法判定。
小结:平行四边形的判定有一个角是直角的平行四边形对角线相等的平行四边形有三个角是直角对角线互相平分且相等
