云南省蒙自市蒙自第一中学2014-2015学年高二下学期开学考试数学(1-21班)试题
文档属性
| 名称 | 云南省蒙自市蒙自第一中学2014-2015学年高二下学期开学考试数学(1-21班)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 223.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-23 14:52:21 | ||
图片预览



文档简介
本试卷分第I卷和第II卷两部分.考试时间:120分钟 满分:150分第Ⅰ卷(选择题)一、选择题:(本大题共12小题,每小题5分,共60分.)
1.集合A=?{x∣},B={x∣x<1},则= ( )
A.{x∣x≥-1} B .{x∣x2} C.{x∣} D.{x∣}
2.若,,与的夹角为,则等于( )
A. B. C. D.
3.不等式组表示的平面区域是( )
A B C D
4.如果偶函数在上是增函数且最小值是2,那么在上是( )
A. 减函数且最小值是 B.. 减函数且最大值是
C. 增函数且最小值是 D. 增函数且最大值是.
5.若数列中,=43-3n,则最大值n =( )
A.13 B.14 C.15 D.14或15
6. 函数的零点个数为 ( )
A. B. C. D.
7.若直线:+与直线: 互相垂直,则的值为( )
A. B. C. 或 D. 1或
8、在下列关于直线、与平面、的命题中,正确的是 ( )
A. 若且,则 , B. 若且,则.
C. 若且,则, D. 若且,则
9.如图所示方格,在每一个方格中填入一个数字,数字可以是中的任何一个,允许重复,则填入方格的数字大于方格的数字的概率为( )
A. B. C. D.
10.已知O是△ABC所在平面内一点,D为BC边中点,且=,那么
A. B. C. D.
11. 已知,,直线和是函数图像的两条相邻的对称轴,则
A. B. C. D.
12.已知且,若恒成立,则实数m的取值范围是
A.(2,4) B.(1, 2) C.(-2,1) D.(-2,4)
第Ⅱ卷(非选择题)
二、填空题:(本大题共4小题,每小题5分,共20分.)
13.一个几何体的三视图如图所示,则该几何体的体积为
14.圆心在原点上与直线相切的圆的方程为 。
15.在△ABC中,若_________。
16.下列命题中正确的有 .
①若是空间三个非零向量,且满足,则;
②回归直线一定过样本中心.
③若将一组样本数据中的每个数据都加上同一个常数后,则样本的方差不变;
④用相关指数R2来刻画回归效果,R2越接近0,说明模型的拟合效果越好;
三、解答题:(本大题共6小题,共70分.解答应写出文字说明、证明过程.)
17、(本小题10分)已知函数.
(I)若,求函数的值; (II)求函数的值域.
18. (本题满分12分)
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.
(I)求的值;
(II)把在前排就坐的高二代表队6人分别记为,现随机从中抽取2人上台抽奖,
求和至少有一人上台抽奖的概率;
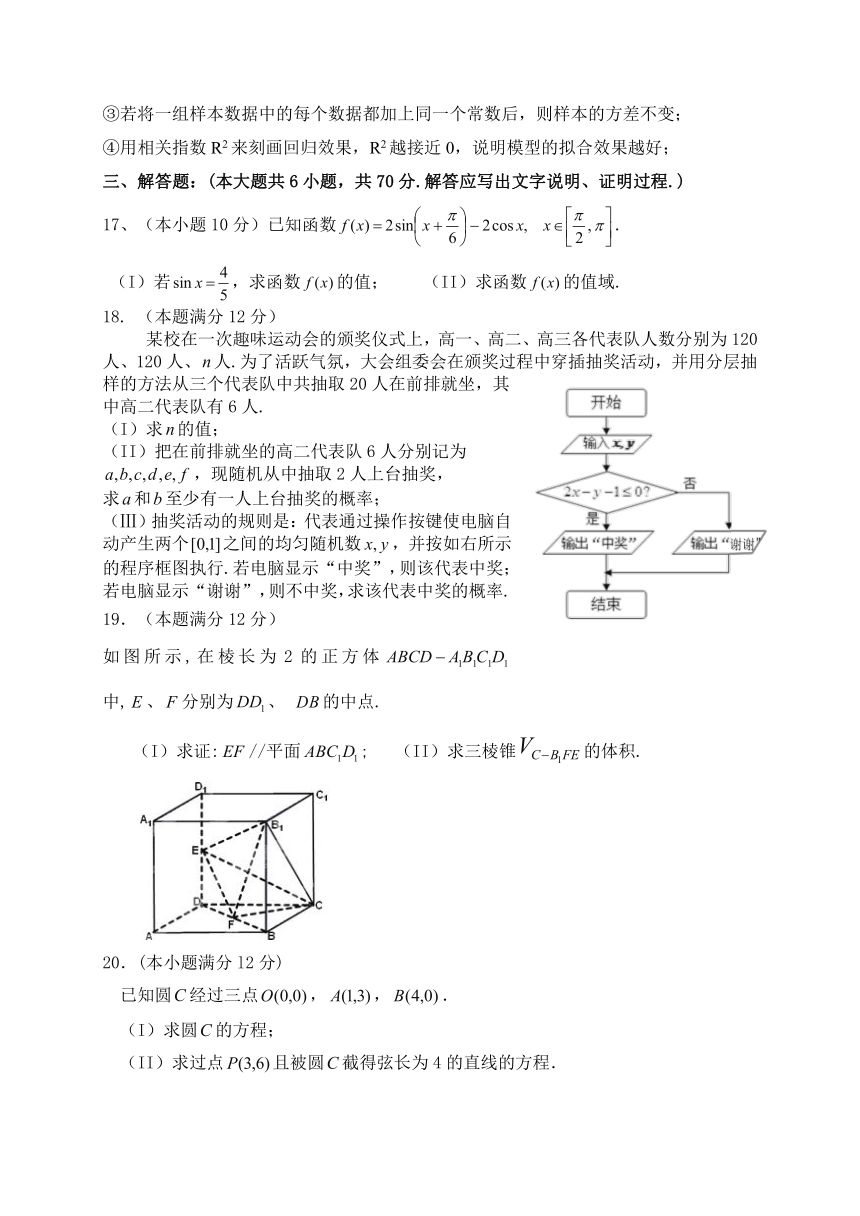
(Ⅲ)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个之间的均匀随机数,并按如右所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
19.(本题满分12分)
如图所示,在棱长为2的正方体中,、分别为、 的中点.
(I)求证://平面; (II)求三棱锥的体积.
20.(本小题满分l2分)
已知圆经过三点,,.
(I)求圆的方程;
(II)求过点且被圆截得弦长为4的直线的方程.
21.(本小题满分12分)在中,所对的边长分别为,设满足条件和, (I)求角A的大小; (II)求的值.
22.(本小题满分12分)
已知数列是首项为1,公比为2的等比数列,数列的前项和.
(I)求数列与的通项公式;
(II)求数列的前项和.
填空题
13. 14. 15. 16.②③
解答题
17. (I)
,
此时. ………………………(5分)
(II),
, , ,
函数的值域为. ………………………(10分)
18.(本小题满分12分)
解:(I)依题意,由,解得………………………2分
(II)记事件为“和至少有一人上台抽奖”, ………………………3分
从高二代表队人中抽取人上台抽奖的所有基本事件列举如下:共15种可能, …………………5分
其中事件包含的基本事件有9种 …………………6分
所以 …………....……7分
(Ⅲ)记事件为“该代表中奖”
如图,所表示的平面区域是以为边的正方形,而中奖所表示的平面区域为阴影部分 ………………………9分
,阴影部分面积……………………11分
所以该代表中奖的概率为………………………12分
19.【答案】 解: (I)连结,在中,、分别为,的中点,则
∵EF为中位线
而面,面
面 ……………………………………………….……4分
(II)
即CF为高 ,
,
∴ 即
∴
=1 .......................12分
20.(I)设圆的方程为,则…3分
解得,,, …………………………………5分
所以圆的方程为. ………………………………6分
(II)①若直线斜率不存在,直线方程为,经检验符合题意; ………8分
②若直线斜率存在,设直线斜率为,则直线方程,
即,则,解得, ………………………10分
所以直线方程为.
综上可知,直线方程为和. …………………12分
21.解:(1)由余弦定理,
又A为三角形大的内角
因此, ……………………………………………(6分)
(II)在△ABC中,∠C=180°-∠A-∠B=120°-∠B.
由已知条件,应用正弦定理
…………………(10分)
tanB…………………(12分)
22.
解:(I)因为数列是首项为1,公比为2的等比数列,
所以数列的通项公式为.………………………(3分)
因为数列的前项和.
所以当时,,
当时,,
所以数列的通项公式为.………………………(6分)
(II)由(1)可知,.
设数列的前项和为,
则 , ①
即 , ②
①-②,得
,
所以.
故数列的前项和为.………………………(12分)
同课章节目录
