两个变量的线性关系

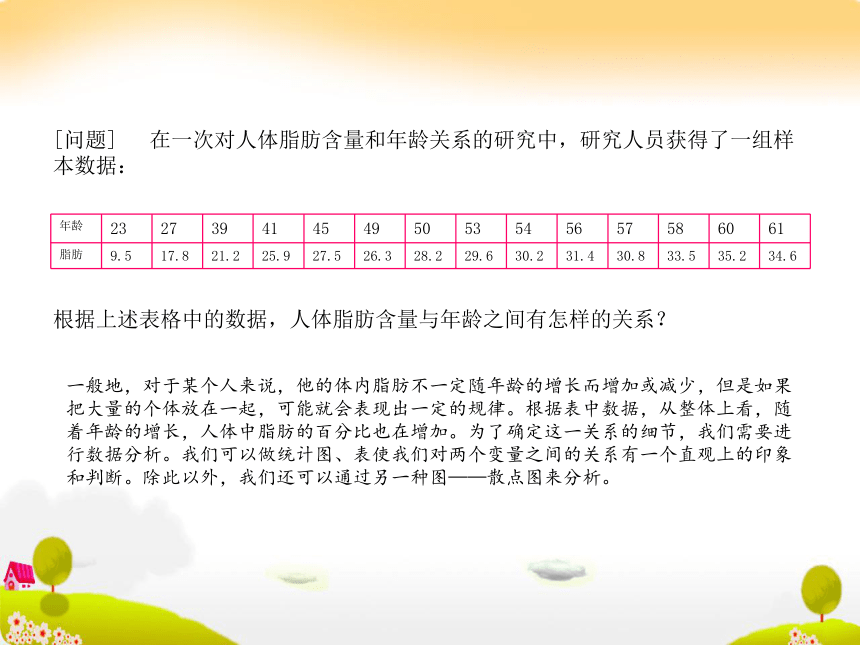
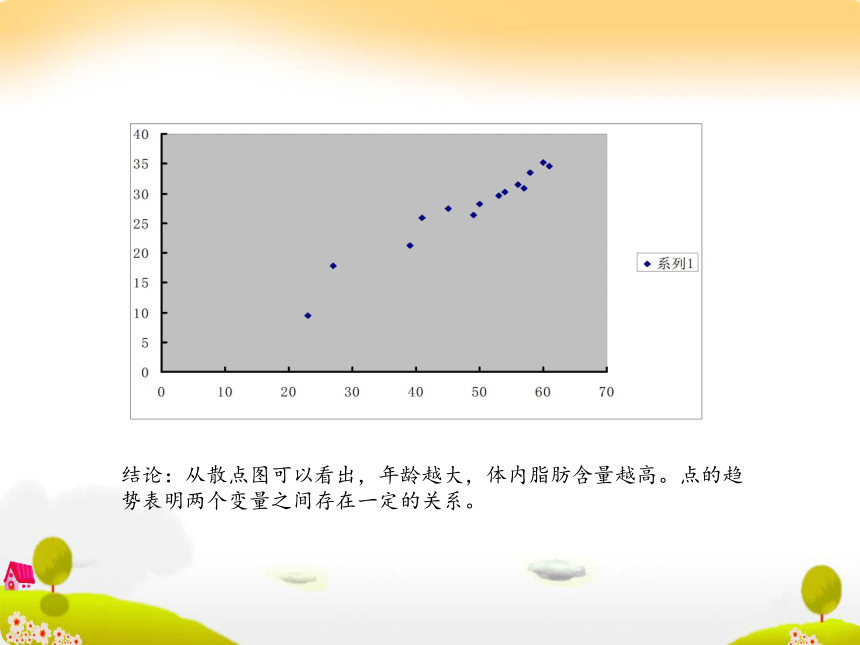
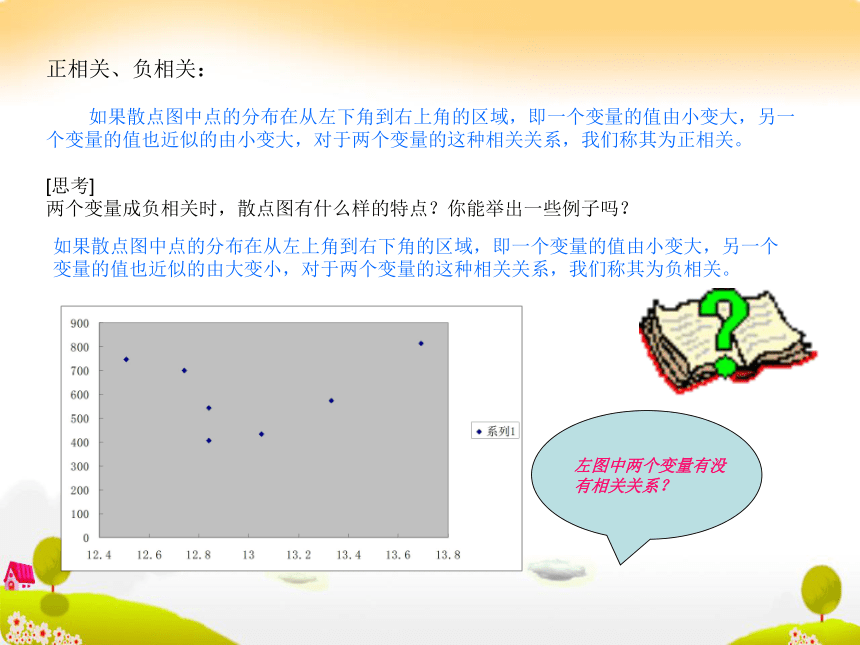
课件12张PPT。两个变量的线性关系[问题] 在一次对人体脂肪含量和年龄关系的研究中，研究人员获得了一组样本数据：根据上述表格中的数据，人体脂肪含量与年龄之间有怎样的关系？一般地，对于某个人来说，他的体内脂肪不一定随年龄的增长而增加或减少，但是如果把大量的个体放在一起，可能就会表现出一定的规律。根据表中数据，从整体上看，随着年龄的增长，人体中脂肪的百分比也在增加。为了确定这一关系的细节，我们需要进行数据分析。我们可以做统计图、表使我们对两个变量之间的关系有一个直观上的印象和判断。除此以外，我们还可以通过另一种图——散点图来分析。结论：从散点图可以看出，年龄越大，体内脂肪含量越高。点的趋势表明两个变量之间存在一定的关系。正相关、负相关： 如果散点图中点的分布在从左下角到右上角的区域，即一个变量的值由小变大，另一个变量的值也近似的由小变大，对于两个变量的这种相关关系，我们称其为正相关。 [思考]两个变量成负相关时，散点图有什么样的特点？你能举出一些例子吗？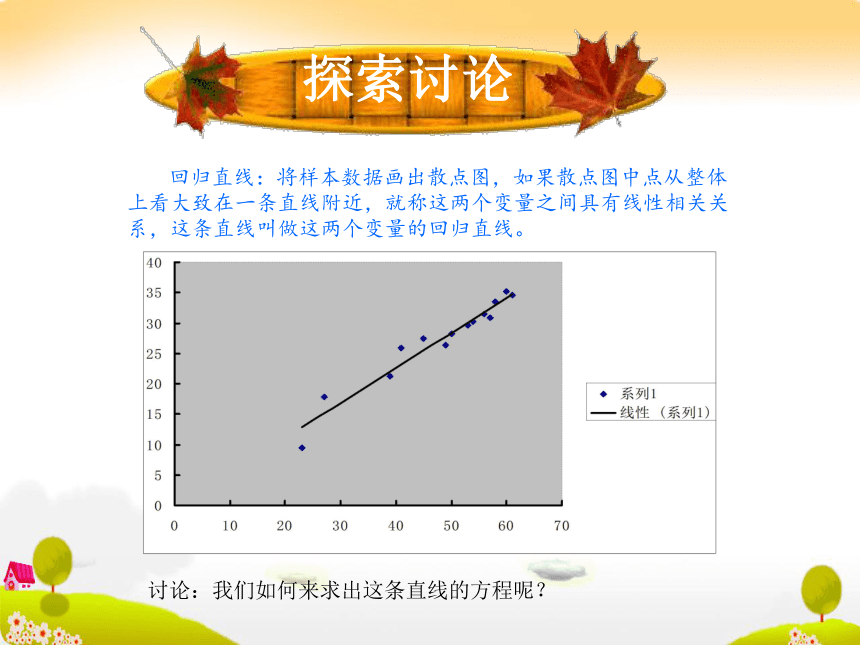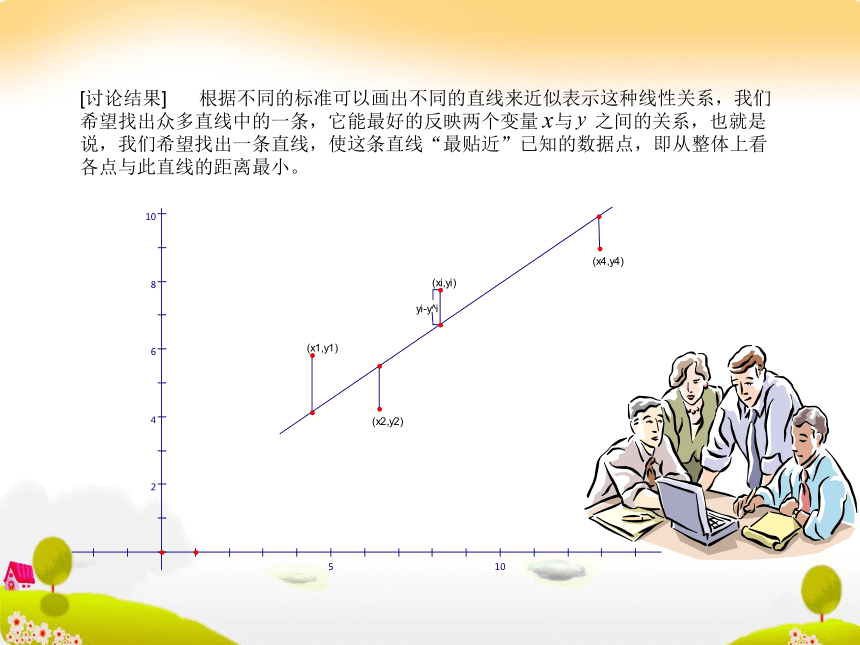 如果散点图中点的分布在从左上角到右下角的区域，即一个变量的值由小变大，另一个变量的值也近似的由大变小，对于两个变量的这种相关关系，我们称其为负相关。左图中两个变量有没有相关关系？ 回归直线：将样本数据画出散点图，如果散点图中点从整体上看大致在一条直线附近，就称这两个变量之间具有线性相关关系，这条直线叫做这两个变量的回归直线。讨论：我们如何来求出这条直线的方程呢？探索讨论[讨论结果] 根据不同的标准可以画出不同的直线来近似表示这种线性关系，我们希望找出众多直线中的一条，它能最好的反映两个变量 与 之间的关系，也就是说，我们希望找出一条直线，使这条直线“最贴近”已知的数据点，即从整体上看各点与此直线的距离最小。 设所求的直线的回归方程为 ，其中 为待定系数，则 ，于是得到各个偏差我们可以用 来表示 个点与回归直线在整体上的接近程度。这样，问题就转化为当 取什么值时 最小。经过运算，可以得到：其中 是回归方程的斜率， 是截距。最小二乘法求回归直线：列表、计算：故可得到：从而得到回归直线方程为：你学会了吗？例1 有一个同学家开了一个小卖部，他为了研究气温对热饮销售的影响，经过统计，得到一个卖出的热饮杯数与当天气温的对比表：（1）画出散点图；
（2）从散点图中发现气温与热饮销售杯数之间的一般规律；
（3）求回归方程；
（4）如果某天的气温是2摄氏度，预测这天卖出的热饮杯数。解：（1）散点图如下：（2）从图中可以看到，各点散布在从左上角到右下角的区域里，因此气温与热饮杯数之间成负相关，即气温越高，卖出的热饮杯数越少。（3）计算可得：因此回归方程为：（4）当时，。因此，某天的气温为2摄氏度时，这天大约可以卖出143杯热饮。练习：课本练习（1）（2）。小结：
（1）两个变量之间的相关关系
（2）用最小二乘法计算回归直线方程作业：
（1）习题2.3
（2）课堂作业：习题2.3 A组3题，B组1题。