第七章 平面直角坐标系复习
文档属性
| 名称 | 第七章 平面直角坐标系复习 |

|
|
| 格式 | zip | ||
| 文件大小 | 228.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-23 00:00:00 | ||
图片预览





文档简介
课件26张PPT。第六章 平面直角坐标系复习课教学目标:
1、掌握本章的各个知识点,并且能够灵活运用;
2、进一步形成数形结合的思想。
重点:
全章知识的归纳与整理。
难点:
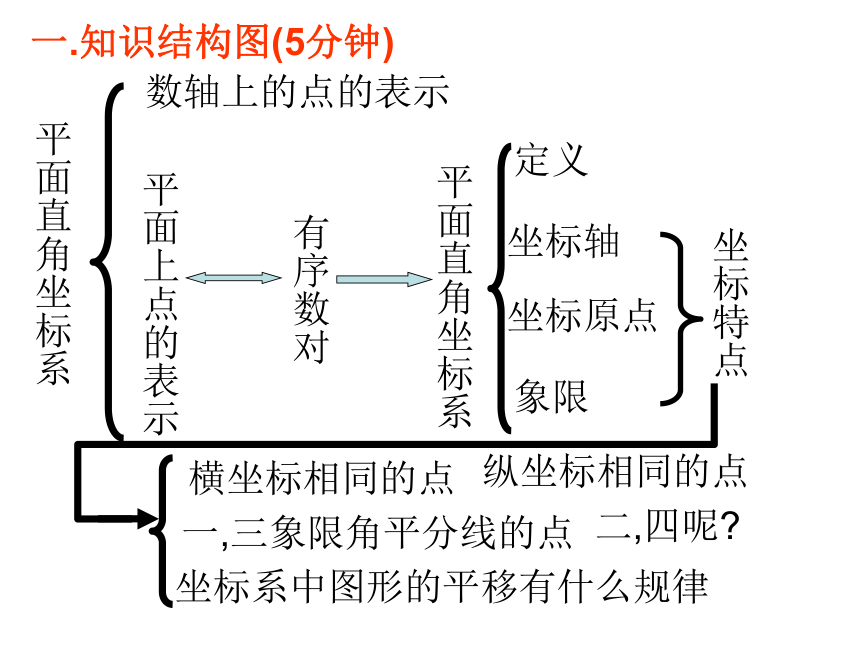
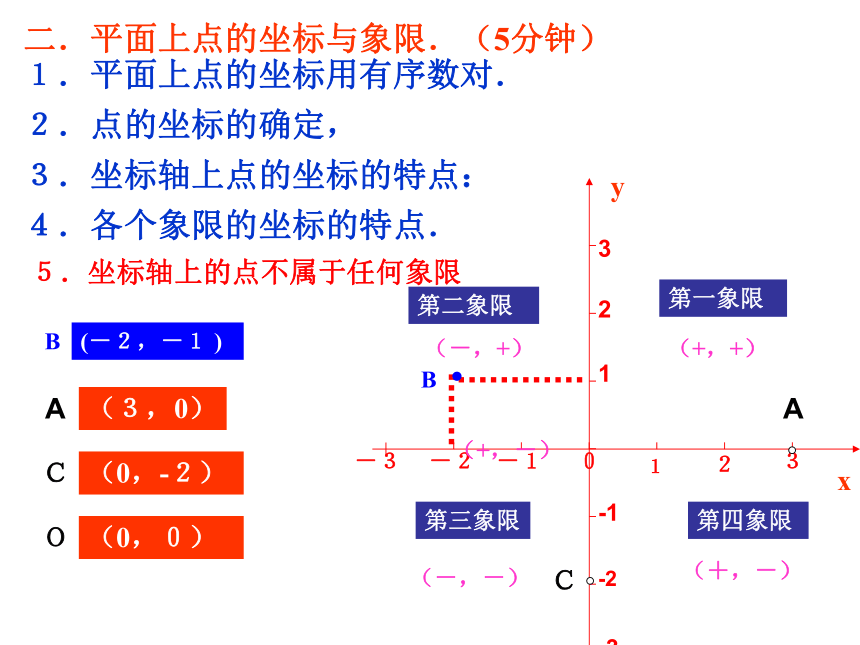
本章知识点的灵活运用。平面直角坐标系数轴上的点的表示平面上点的表示有序数对平面直角坐标系定义坐标轴坐标原点象限坐标特点横坐标相同的点纵坐标相同的点一,三象限角平分线的点二,四呢?坐标系中图形的平移有什么规律一.知识结构图(5分钟)·C2.点的坐标的确定,1.平面上点的坐标用有序数对.3.坐标轴上点的坐标的特点:4.各个象限的坐标的特点.二.平面上点的坐标与象限.(5分钟)AC第一象限第二象限第三象限第四象限(+,+)(-,+)(-,-)(+,-)(+,-)xyB(-2,-1 )(3,0)(0,-2)·BAC5.坐标轴上的点不属于任何象限O(0,0)1.想一想:下列各点分别在坐标平面的什么位置上?A(3,2) B(0,-2)
C(-3,-2) D(-3,0)
E(-1.5,3.5) F(2,-3)第一象限第三象限第二象限第四象限y轴上x轴上2.点P(x,y)的坐标x,y,满足xy=0,则点P在 . 4.甲同学从A(1,0)出发,向东走2个单位,再向北走3个单位到达B( , ) 5.点A(x,y)在第二象限,满足 求A的坐标 . 6.点A(x,y),且x+y>0, 那么点A在第___象限3.点A(1+m,2m+1)在x轴上,则m=___,此时A的坐标_______练一练8.实数 x,y满足 (x-1)2+ ︳y︱ = 0,则点 P( x,y)在【 】. (A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置
9. x,y满足 x2+ y2= 0,则点 P( x,y)在 ( ) (A)原点 (B)x轴正半轴
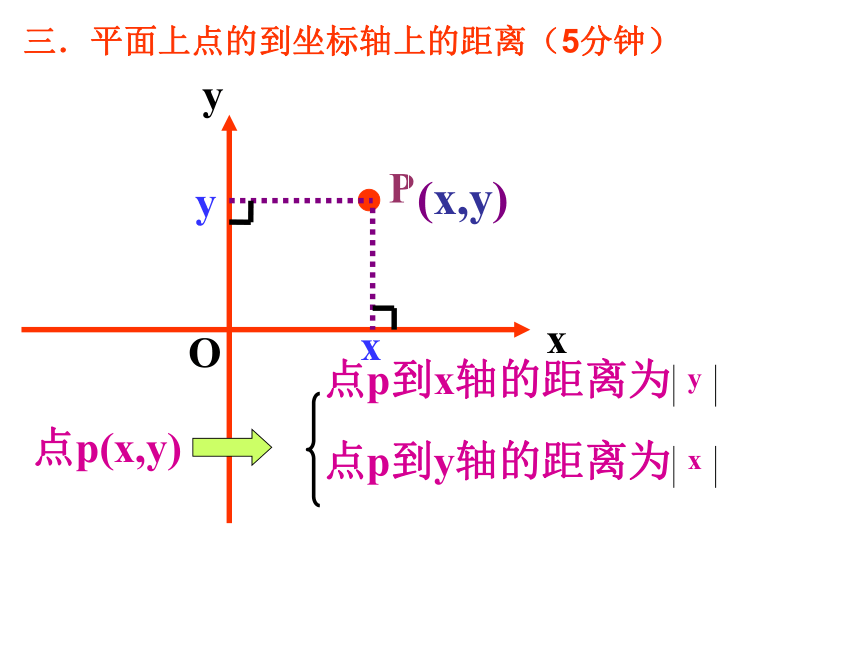
(C)第一象限 (D)任意位置 Axy(x,y)点p(x,y)点p到x轴的距离为点p到y轴的距离为
三.平面上点的到坐标轴上的距离(5分钟) 3.点A在y轴上,距离原点4个单位.则A的坐标是 .4.点A在y轴的右侧,距离y轴4个单位,距离x轴3个单
位,则A的坐标是 .练习:2.点P(a,b)到x轴的距离是 ,到y轴的距离是 .1.点P(1,-4)到x轴的距离是 ,到y轴的距离是 .6、点P(a-2,2a+3)到两坐标轴的距离相等,则a= .5.点P在x轴的下方,距离x轴4个单位;y轴的左侧,距离y轴的距离3个单位,则P的坐标是P( )7、点 A 在第一象限,当 m 为何值( 2.2 )时,
点 A( m + 1,3m - 5)到 x轴的距离是它到
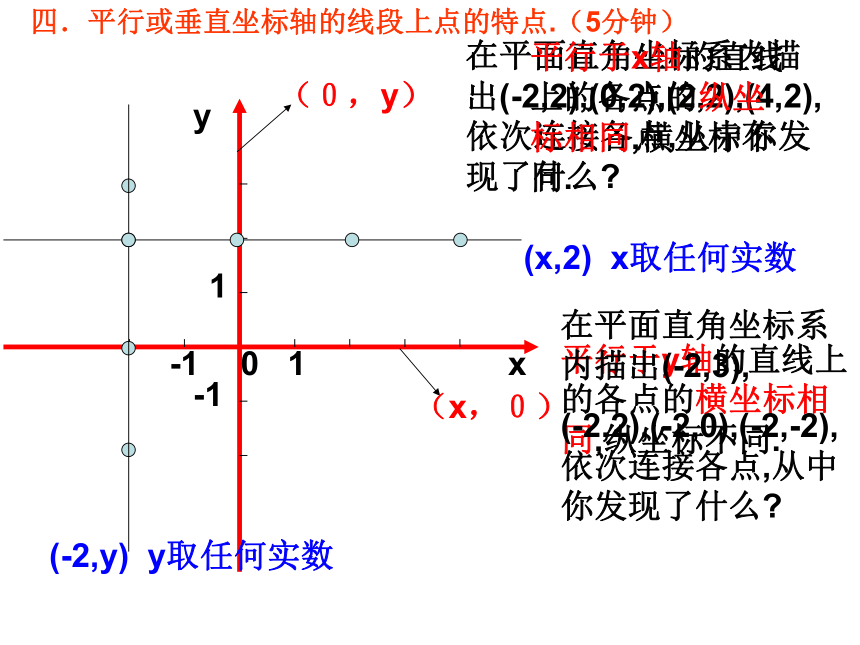
y轴距离的一半 .(x,0)(0,y)在平面直角坐标系内描出(-2,2),(0,2),(2,2),(4,2),依次连接各点,从中你发现了什么?平行于x轴的直线上的各点的纵坐标相同,横坐标不同.平行于y轴的直线上的各点的横坐标相同,纵坐标不同.在平面直角坐标系内描出(-2,3),
(-2,2),(-2,0),(-2,-2),依次连接各点,从中你发现了什么?(x,2) x取任何实数(-2,y) y取任何实数四.平行或垂直坐标轴的线段上点的特点.(5分钟)1.已知A(4,2)、B(4,7),则线段AB的位置特点是 与x轴 .与y轴 .练习:2、若不同的两点A(2,a),B(b,-4), 直线AB与x轴平行,则a= ,b= .3,、若不同的两点A(2,a),B(b,-4), 直线AB与y轴平行,则a= ,b= .4、A(a,-2),B(4,-2)且AB=6,由条件写出a= .5、A(a,b),B(4,-2),线段平行于y轴,且AB=6,由条件写出A的坐标是 .6、如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( ) (A)平行于x轴 (B)平行于y轴
(C)经过原点 (D)以上都不对3.将A(-3,2)向右平移4个单位,再向上平移1个单位得到B的坐标( ).五.点的平移与点坐标的变化.(5分钟)1.将A(-3,2)向左平移2个单位,得点的坐标为 .2.将A(-3,2)向下平移2个单位,得点的坐标为 .5.将A(x,y)通过平移得点的坐标为A/(x+3,y-2),则先A向 平移 个单位,再向 平移 个单位。 4.将点A(2,3)向__平移__个单位,再向__平移__个单位后与点B(-3,5)重合6.A(1,2),B(2,3),将线段AB平移得到CD,点A的对应点C坐标为 (0,4),则点D的坐标为 . 平移前点的坐标+平移方式=平移后点的坐标7.四边形A(-2,1),B(3,-1),C(2,4),D(-1,2)将四边形ABCD向右平移2个单位,再向上平移1个单位。(1)求得到的另一个四边形各顶点的坐标(2)移动后的四边形的面积(3)如果将原四边形的横坐标增加6,纵坐标减少5.求新四边形的面积。(4)如果将原四边形的横、纵坐标都扩大2倍,那么新四边形与原四边形的形状、大小比较有什么变化?
ABCD六.求三角形、四边形的面积(5分钟)A(2,4)BO1、求△AOB的面积ABCDE(2,0)F2.求四边形ABCD的面积A(-4,0)B(-0.5,0)O3、已知△AOB的面积为14,A(-4,0)B(-0.5,0).求点C的坐标。xyC1.矩形ABCD的长为4,宽为3,建立适当的直角坐标系,并写出各点的坐标.ABCD还有其他方法吗xxyy七.建立适当的直角坐标系解题(5分钟)3.第一次将⊿OAB变成⊿OA1B1,第二次将⊿OA1B1变换成⊿OA2B2,再将⊿OA2B2变换成⊿OA3B3,已知A(1,3),A1(2,3),A2(4,3),A3(8,3);B(2,0),B1(4,0),B2(8,0),B3(16,0).A4的坐标 , B4的坐标 . An的坐标 , Bn的坐标 .AA1A2A3BB1B2B33OP(x,y)A(x,-y)B(-x,y)C(-x,-y)补充:八、对称点的坐标特征(5分钟) 已知p1(x1,y1), p2(x2,y2),填表:x1=x2x1= - x2 y1= y2 y1= -y2x1= - x2y1= -y2关于X轴对称关于Y轴对称关于原点对称 基本题: 1.在 y轴上的点的横坐标是( ),在 x轴上的点的纵坐标是( ). 2.点 A(2,- 3)关 于 x 轴 对 称 的 点 的 坐 标 是( ). 3.点 B( - 2,1)关 于 y 轴 对 称 的 点 的 坐 标 是( ). 002,32,131425-2-4-1-3xyA(2,2)B(-3,-3)C(-1,1)D(4,-4)补充:九、象限角平分线上的点的坐标特征(5分钟)象限角平分线上的点的坐标特征已知p(x,y),填表:y = x 或y-x=0y = - x或y+x=0已知点(a,3)在第一象限内两条坐标轴夹角的平分线上,则a= 。3补充:十、与点p(x,y)有关的距离:1、点P到原点的距离为2、连接点A(x1,y1),B(X2,Y2)的线段 的中点p(x,y)的坐标关系是:
2x=x1+y1,2y=X2+Y2小结:本节课中你的收获是什么?
作业:复习题7 第7、8、10题
教学反思:
对于学生易出错的问题,应加以强调和练习。
1、掌握本章的各个知识点,并且能够灵活运用;
2、进一步形成数形结合的思想。
重点:
全章知识的归纳与整理。
难点:
本章知识点的灵活运用。平面直角坐标系数轴上的点的表示平面上点的表示有序数对平面直角坐标系定义坐标轴坐标原点象限坐标特点横坐标相同的点纵坐标相同的点一,三象限角平分线的点二,四呢?坐标系中图形的平移有什么规律一.知识结构图(5分钟)·C2.点的坐标的确定,1.平面上点的坐标用有序数对.3.坐标轴上点的坐标的特点:4.各个象限的坐标的特点.二.平面上点的坐标与象限.(5分钟)AC第一象限第二象限第三象限第四象限(+,+)(-,+)(-,-)(+,-)(+,-)xyB(-2,-1 )(3,0)(0,-2)·BAC5.坐标轴上的点不属于任何象限O(0,0)1.想一想:下列各点分别在坐标平面的什么位置上?A(3,2) B(0,-2)
C(-3,-2) D(-3,0)
E(-1.5,3.5) F(2,-3)第一象限第三象限第二象限第四象限y轴上x轴上2.点P(x,y)的坐标x,y,满足xy=0,则点P在 . 4.甲同学从A(1,0)出发,向东走2个单位,再向北走3个单位到达B( , ) 5.点A(x,y)在第二象限,满足 求A的坐标 . 6.点A(x,y),且x+y>0, 那么点A在第___象限3.点A(1+m,2m+1)在x轴上,则m=___,此时A的坐标_______练一练8.实数 x,y满足 (x-1)2+ ︳y︱ = 0,则点 P( x,y)在【 】. (A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置
9. x,y满足 x2+ y2= 0,则点 P( x,y)在 ( ) (A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置 Axy(x,y)点p(x,y)点p到x轴的距离为点p到y轴的距离为
三.平面上点的到坐标轴上的距离(5分钟) 3.点A在y轴上,距离原点4个单位.则A的坐标是 .4.点A在y轴的右侧,距离y轴4个单位,距离x轴3个单
位,则A的坐标是 .练习:2.点P(a,b)到x轴的距离是 ,到y轴的距离是 .1.点P(1,-4)到x轴的距离是 ,到y轴的距离是 .6、点P(a-2,2a+3)到两坐标轴的距离相等,则a= .5.点P在x轴的下方,距离x轴4个单位;y轴的左侧,距离y轴的距离3个单位,则P的坐标是P( )7、点 A 在第一象限,当 m 为何值( 2.2 )时,
点 A( m + 1,3m - 5)到 x轴的距离是它到
y轴距离的一半 .(x,0)(0,y)在平面直角坐标系内描出(-2,2),(0,2),(2,2),(4,2),依次连接各点,从中你发现了什么?平行于x轴的直线上的各点的纵坐标相同,横坐标不同.平行于y轴的直线上的各点的横坐标相同,纵坐标不同.在平面直角坐标系内描出(-2,3),
(-2,2),(-2,0),(-2,-2),依次连接各点,从中你发现了什么?(x,2) x取任何实数(-2,y) y取任何实数四.平行或垂直坐标轴的线段上点的特点.(5分钟)1.已知A(4,2)、B(4,7),则线段AB的位置特点是 与x轴 .与y轴 .练习:2、若不同的两点A(2,a),B(b,-4), 直线AB与x轴平行,则a= ,b= .3,、若不同的两点A(2,a),B(b,-4), 直线AB与y轴平行,则a= ,b= .4、A(a,-2),B(4,-2)且AB=6,由条件写出a= .5、A(a,b),B(4,-2),线段平行于y轴,且AB=6,由条件写出A的坐标是 .6、如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( ) (A)平行于x轴 (B)平行于y轴
(C)经过原点 (D)以上都不对3.将A(-3,2)向右平移4个单位,再向上平移1个单位得到B的坐标( ).五.点的平移与点坐标的变化.(5分钟)1.将A(-3,2)向左平移2个单位,得点的坐标为 .2.将A(-3,2)向下平移2个单位,得点的坐标为 .5.将A(x,y)通过平移得点的坐标为A/(x+3,y-2),则先A向 平移 个单位,再向 平移 个单位。 4.将点A(2,3)向__平移__个单位,再向__平移__个单位后与点B(-3,5)重合6.A(1,2),B(2,3),将线段AB平移得到CD,点A的对应点C坐标为 (0,4),则点D的坐标为 . 平移前点的坐标+平移方式=平移后点的坐标7.四边形A(-2,1),B(3,-1),C(2,4),D(-1,2)将四边形ABCD向右平移2个单位,再向上平移1个单位。(1)求得到的另一个四边形各顶点的坐标(2)移动后的四边形的面积(3)如果将原四边形的横坐标增加6,纵坐标减少5.求新四边形的面积。(4)如果将原四边形的横、纵坐标都扩大2倍,那么新四边形与原四边形的形状、大小比较有什么变化?
ABCD六.求三角形、四边形的面积(5分钟)A(2,4)BO1、求△AOB的面积ABCDE(2,0)F2.求四边形ABCD的面积A(-4,0)B(-0.5,0)O3、已知△AOB的面积为14,A(-4,0)B(-0.5,0).求点C的坐标。xyC1.矩形ABCD的长为4,宽为3,建立适当的直角坐标系,并写出各点的坐标.ABCD还有其他方法吗xxyy七.建立适当的直角坐标系解题(5分钟)3.第一次将⊿OAB变成⊿OA1B1,第二次将⊿OA1B1变换成⊿OA2B2,再将⊿OA2B2变换成⊿OA3B3,已知A(1,3),A1(2,3),A2(4,3),A3(8,3);B(2,0),B1(4,0),B2(8,0),B3(16,0).A4的坐标 , B4的坐标 . An的坐标 , Bn的坐标 .AA1A2A3BB1B2B33OP(x,y)A(x,-y)B(-x,y)C(-x,-y)补充:八、对称点的坐标特征(5分钟) 已知p1(x1,y1), p2(x2,y2),填表:x1=x2x1= - x2 y1= y2 y1= -y2x1= - x2y1= -y2关于X轴对称关于Y轴对称关于原点对称 基本题: 1.在 y轴上的点的横坐标是( ),在 x轴上的点的纵坐标是( ). 2.点 A(2,- 3)关 于 x 轴 对 称 的 点 的 坐 标 是( ). 3.点 B( - 2,1)关 于 y 轴 对 称 的 点 的 坐 标 是( ). 002,32,131425-2-4-1-3xyA(2,2)B(-3,-3)C(-1,1)D(4,-4)补充:九、象限角平分线上的点的坐标特征(5分钟)象限角平分线上的点的坐标特征已知p(x,y),填表:y = x 或y-x=0y = - x或y+x=0已知点(a,3)在第一象限内两条坐标轴夹角的平分线上,则a= 。3补充:十、与点p(x,y)有关的距离:1、点P到原点的距离为2、连接点A(x1,y1),B(X2,Y2)的线段 的中点p(x,y)的坐标关系是:
2x=x1+y1,2y=X2+Y2小结:本节课中你的收获是什么?
作业:复习题7 第7、8、10题
教学反思:
对于学生易出错的问题,应加以强调和练习。
