第五单元 简易方程思维拓展百分练(试题)人教版五年级上册数学(含解析)
文档属性
| 名称 | 第五单元 简易方程思维拓展百分练(试题)人教版五年级上册数学(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 205.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 21:37:40 | ||
图片预览




文档简介
人教版五年级数学上册第五单元简易方程思维拓展百分练
一、选择题(共16分)
1.郑州市动物园位于郑州市金水区花园路北段,是河南省唯一一座专业性动物园。周末苗苗到动物园参观,发现一片园区里养有单峰骆驼和双峰骆驼,她数了数共有36个头,48个驼峰,那么这个园区内共有( )头双峰骆驼。
A.24 B.12 C.18 D.6
2.数m、n、t按数值大小在直线上的位置如下,与数t最接近的是( )。
A.n×m B.n+m C.n÷m D.n-m
3.小正方形的边长是a厘米,大正方形的边长等于小正方形的周长,大正方形的面积是( )平方厘米。
A. B. C. D.
4.水果店运来15箱苹果和10箱橘子,其重1520kg。已知每箱苹果重25kg,求每箱橘子重多少千克。设每箱橘子重xkg,以下方程不能成立的是( )。
A. B.
C. D.
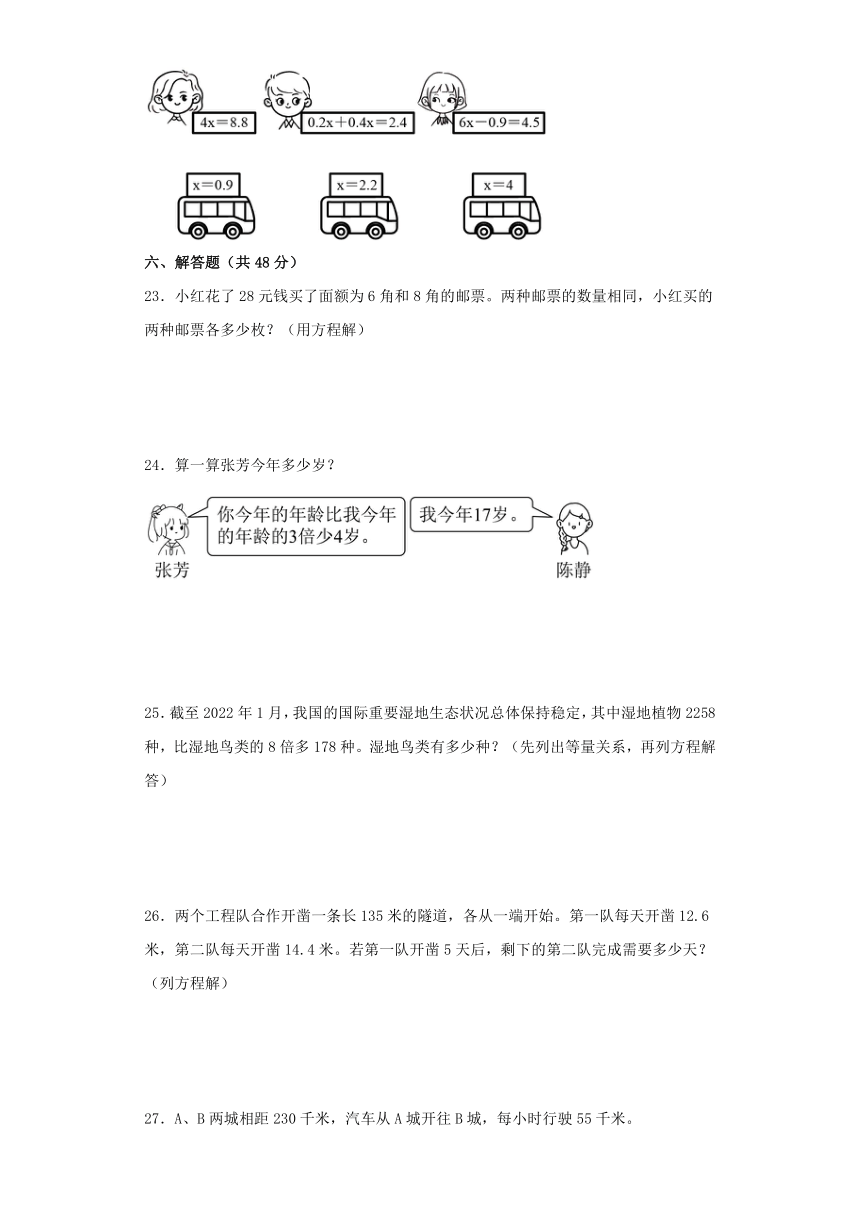
5.小明把5x+0.4错写成了5(x+0.4),结果比原来( )。
A.多0.4 B.少0.4 C.少1.6 D.多1.6
6.有m个馄饨(m为整十数),每碗装10个,可以装( )碗。
A. B. C. D.
7.福州西湖公园至今有一千七百多年的历史,是福州迄今为止保留最完整的一座古典园林,被称为“福建园林明珠”,现占地面积为42.51公顷,其中陆地面积是12.21公顷,水面面积是x公顷。根据其中的数量关系,下列方程正确的是( )。
A. B.
C. D.
8.小明把6(x+4)错写成了6x+4,结果比原来( )。
A.多20 B.多4 C.少20 D.少4
二、填空题(共16分)
9.服装厂的工人每人每天可以生产5件上衣或8条裤子,一件上衣和一条裤子为一套服装。现有104名工人,每天最多能生产( )套服装。
10.根据题意找出等量关系,并且列出方程。
张明买了4本练习本,每本x元,付给售货员10元,找回4元。( )
11.箱子里有同样数量的苹果和梨。小东每次从这个箱子里取出5个苹果和2个梨,取了几次后,苹果没有了,梨还剩18个。箱子里原来有( )个梨。
12.在括号里填上含有字母的式子。
(1)一辆卡车运x吨煤,共运了3次,平均每次运煤( )吨。
(2)五年级学生小丽和爸爸妈妈一起去公园,公园的成人门票是每张a元,学生门票是每张b元。小丽一家三口共需付( )元购买门票。
13.水果店运来a箱橘子,运来的苹果比橘子多5箱,运来苹果( )箱。当a=18时,水果店共运来( )箱水果。
14.定义新运算“ ”,A B=(A-2)×B,如果A 5=30,那么A=( )。
15.小红拿着x元钱买了单价为15元的大枣2千克,应找回( )元;若x=50,应找回( )元。
16.最新研究发现,真空管道中高速列车的时速(即每小时行的路程),比现在高铁时速的3倍还快150千米。高铁时速a千米,真空管道中高速列车的时速是( )千米。
三、判断题(共8分)
17.学校组织研学活动,租用大巴车和小巴车共8辆,大巴车每辆600元,小巴车每辆450元。如果租用的大巴车为a辆,那么租用小巴车的费用是450×(8-a)元。( )
18.有两个数和b,都大于1,两数相乘,它们的积比大。( )
19.甲数比乙数小6,如果甲数是a,则乙数是a-6。( )
20.如果数对(3,)和(,4)表示的位置在同一列,那么=3。( )
四、计算题(共6分)
21.解方程。
6x-2.7=1.5 8(x-1.6)=8.64
7x-4.3×6=9.34 4x+1.6x=16.8
五、连线题(共6分)
22.找出方程的解,连一连。
六、解答题(共48分)
23.小红花了28元钱买了面额为6角和8角的邮票。两种邮票的数量相同,小红买的两种邮票各多少枚?(用方程解)
24.算一算张芳今年多少岁?
25.截至2022年1月,我国的国际重要湿地生态状况总体保持稳定,其中湿地植物2258种,比湿地鸟类的8倍多178种。湿地鸟类有多少种?(先列出等量关系,再列方程解答)
26.两个工程队合作开凿一条长135米的隧道,各从一端开始。第一队每天开凿12.6米,第二队每天开凿14.4米。若第一队开凿5天后,剩下的第二队完成需要多少天?(列方程解)
27.A、B两城相距230千米,汽车从A城开往B城,每小时行驶55千米。
(1)开出t小时后汽车离A城有多远?如果t=2.4,汽车离开A城有多远?
(2)开出t小时后汽车离B城有多远?如果t=3.4,汽车距离B城有多远?
28.近年来,网购的蓬勃发展方便了人们的生活。某快递分派站现有包裹若干件需快递员派送。若每个快递员派送10件,还剩6件;若每个快递员派送12件,还差6件。该分派站现有包裹多少件?快递员多少名?
29.五年级同学乘车去博物馆参观。如果租5辆车,则有10名同学没有座位;如果租6辆车,则多出32个座位。
(1)每辆车上有多少个座位?(列方程解答)
(2)一共有多少名同学去博物馆参观?
30.某市为更有效地利用水资源,制定了居民用水收费标准:如果一户每月用水量不超过15立方米,每立方米按1.8元收费;如果超过15立方米,超过部分按每立方米2.3元收费。另外,每立方米加收污水处理费1元。若某户一月份共支付水费58.5元,求该户一月份用水量。
参考答案
1.B
【分析】设这个园区内共有x头双峰骆驼,则单峰骆驼有(36-x)头,单峰骆驼数量×1+双峰骆驼×2=48,据此列出方程求出x的值即可。
【详解】解:设这个园区内共有x头双峰骆驼。
(36-x)×1+2x=48
36-x+2x=48
36+x=48
36+x-36=48-36
x=12
这个园区内共有12头双峰骆驼。
故答案为:B
【点睛】本题考查鸡兔同笼问题,用方程解决问题的关键是找到等量关系。
2.C
【分析】看图,可以假设n为0.7,m为0.3,从而求出选项中式子的值。t在2和3之间,据此找出与数t最接近的式子。
【详解】令n=0.7,m=0.3,
A.n×m=0.7×0.3=0.21;
B.n+m=0.7+0.3=1;
C.n÷m=0.7÷0.3≈2.33;
D.n-m=0.7-0.3=0.4;
又因为t>2,所以与数t最接近的是n÷m。
故答案为:C
【点睛】本题考查了含有字母式子的求值,有一定计算能力是解题的关键。
3.D
【分析】正方形的周长=边长×4,代入字母表示出大正方形的边长,再代入正方形的面积公式:S=a2计算即可。
【详解】(厘米)
(平方厘米)
大正方形的面积是平方厘米。
故答案为:D。
【点睛】本题主要考查用字母表示数,熟记正方形周长、面积公式是解题的关键。
4.A
【分析】由题意可知,苹果的重量为15×25kg,橘子的重量为10xkg,再根据等量关系:苹果的重量+橘子的重量=1520、苹果的重量=1520-橘子的重量或橘子的重量=1520-苹果的重量,据此列方程即可。
【详解】A.因为橘子的重量≠橘子和苹果的总量+苹果的重量,所以不成立;
B.因为橘子和苹果的总量-苹果的重量=橘子的重量,则可列方程为:,该方程成立;
C.因为苹果的重量+橘子的重量=1520,则可列方程为:,该方程成立;
D.因为苹果的重量=1520-橘子的重量,则可列方程为:,该方程成立。
故答案为:A
【点睛】本题考查用方程解决实际问题,明确等量关系是解题的关键。
5.D
【分析】采用赋值法,假设x=4,将x=4分别代入5x+0.4和5(x+0.4),分别求值,再求差即可。
【详解】假设x=4
5x+0.4
=5×4+0.4
=20+0.4
=20.4
5(x+0.4)
=5×(4+0.4)
=5×4+5×0.4
=20+2
=22
22-20.4=1.6
小明把5x+0.4错写成了5(x+0.4),结果比原来多1.6。
故答案为:D
6.D
【分析】用馄饨的总数量除以每碗装馄饨的数量,即可求出可以装多少碗。
【详解】(m÷10)碗
有m个馄饨(m为整十数),每碗装10个,可以装(m÷10)碗。
故答案为:D
7.A
【分析】根据题意,可知陆地面积+水面面积=占地面积,据此列出方程为。据此选择即可。
【详解】根据其中的数量关系,下列方程正确的是。
故答案为:A
8.C
【分析】先算出6(x+4),展开可知比6x+4大,所以再减去6x+4,即可算出答案。
【详解】6(x+4)
=6x+6×4
=6x+24
6x+24-(6x+4)
=6x-6x+24-4
=20
所以结果比原来少20。
故答案为:C
9.320
【分析】要使每天生产的套装最多,必须使生产的上衣和裤子的数量相等,人员分工合理,据此设生产上衣的人数为x人,则生产裤子的人数为(104-x)人,据此列方程解答。
【详解】解:设生产上衣的人数为x人,则生产裤子的人数为(104-x)人。
5x=8×(104-x)
5x=8×104-8x
5x+8x=8×104-8x+8x
13x=832
13x÷13=832÷13
x=64
5×64=320(套)
则每天最多能生产320套服装。
10.4本练习本的钱数+找回的钱=10元;4+4x=10
【分析】根据题意可知,4本练习本的总价加上找回的钱等于付出的钱,根据总价=单价×数量,每本为x元,则4本是4x元,据此列方程解答。
【详解】等量关系:4本练习本的钱数+找回的钱=10元
列出的方程:4+4x=10
【点睛】此题考查了学生列方程的能力,找准等量关系是解题的关键。
11.30
【分析】根据“箱子里有同样数量的苹果和梨”可得等量关系:每次取出苹果的个数×取的次数=每次取出梨的个数×取的次数+梨还剩下的个数;据此列出方程,并求解。
【详解】解:设取了次。
5=2+18
5-2=2+18-2
3=18
3÷3=18÷3
=6
梨:
2×6+18
=12+18
=30(个)
箱子里原来有30个梨。
【点睛】本题考查列方程解决问题,从题目中找到等量关系,按等量关系列出方程。
12.(1)x÷3
(2)2a+b/b+2a
【分析】(1)将煤的总量x吨除以3次,表示出平均每次运煤多少吨;
(2)将2张成人票票价加上1张儿童票票价,表示出购买门票一共需要付多少元。
【详解】(1)一辆卡车运x吨煤,共运了3次,平均每次运煤(x÷3)吨。
(2)小丽一家三口共需付(2a+b)元购买门票。
【点睛】本题考查了用字母表示数,有一定抽象概括能力是解题的关键,同时要注意数字和字母相乘,中间的乘号省略,数字在前,字母在后。
13. a+5 41
【分析】根据题意可知,橘子的箱数+5箱=苹果的箱数,据此可知,运来的苹果有(a+5)箱,然后把a=18代入a+5计算即可。
【详解】据分析可知,运来的苹果有(a+5)箱;
当a=18时,
苹果:18+5=23(箱)
共:23+18=41(箱)
水果店运来a箱橘子,运来的苹果比橘子多5箱,运来苹果(a+5)箱。当a=18时,水果店共运来41箱水果。
【点睛】本题主要考查了用字母表示数以及含未知数式子的求值,找到相应的数量关系式是解答本题的关键。
14.8
【分析】这道题规定的运算本质是:运算符号前面的数减去2,再乘运算符号后面的数。据此由A 5=30,则有(A-2)×5=30。再解关于A的方程,可求出A的值。
【详解】(A-2)×5=30
解:(A-2)×5÷5=30÷5
A-2=6
A-2+2=6+2
A=8
【点睛】解答定义新运算,关键是要正确地理解新定义的算式含义,然后严格按照新定义的计算程序,将数值代入,转化为常规的四则运算算式进行计算。
15. x-30 20
【分析】根据总价=单价×数量,求出总价,再用x元减去总价,表示出应找回多少元。再把x=50代入式子,计算即可解答。
【详解】x-15×2=x-30
50-30=20(元)
所以,应找回(x-30)元;若x=50,应找回20元。
【点睛】本题考查了用字母表示数,有一定抽象概括能力是解题的关键。
16.3a+150
【分析】根据题意可得出数量关系:高铁的时速×3+150=真空管道中高速列车的时速,据此用含字母的式子表示真空管道中高速列车的时速。
【详解】a×3+150=(3a+150)千米
真空管道中高速列车的时速是(3a+150)千米。
17.√
【分析】根据题意,租用大巴车和小巴车共8辆,其中租用的大巴车为a辆,那么租用小巴车为(8-a)辆;根据“单价×数量=总价”可得出数量关系:租用每辆小巴车的价钱×租用小巴车的数量=租用小巴车的费用,据此用含字母的式子表示租用小巴车的费用。
【详解】每辆小巴车450元,租用小巴车(8-a)辆,那么租用小巴车的费用是450×(8-a)元。
原题说法正确。
故答案为:√
【点睛】本题考查用字母表示式子,根据单价、数量、总价之间的关系得出数量关系,按数量关系写出含字母的式子。
18.√
【分析】根据积与因数的关系可知:当一个数乘一个大于1的数,所得的积比这个数大。据此判断。
【详解】令a=1.1,b=2,
则:1.1×2=2.2
2.2>1.1
原题说法正确。
故答案为:√
【点睛】掌握积与因数的关系是解答的关键。
19.×
【分析】已知甲数比乙数小6,则甲数=乙数-6,甲数+6=乙数,所以如果甲数是a,则乙数是a+6。
【详解】甲数比乙数小6,如果甲数是a,则乙数是a+6。原题干说法错误。
故答案为:×
20.√
【分析】用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行。
数对(3,)表示在第3列第行,数对(,4)表示在第列第4行;如果(3,)和(,4)表示的位置在同一列,由此可得出的值。
【详解】如果数对(3,)和(,4)表示的位置在同一列,那么=3。
原题说法正确。
故答案为:√
21.x=0.7;x=2.68;
x=5.02;x=3
【分析】(1)根据等式的性质,在方程两边同时加上2.7,再同时除以6即可;
(2)根据等式的性质,在方程两边同时除以8,再同时加上1.6即可;
(3)把原方程化简为7x-25.8=9.34,再根据等式的性质,在方程两边同时加上25.8,最后再同时除以7即可;
(4)把原方程化简为5.6x=16.8,再根据等式的性质,在方程两边同时除以5.6即可。
【详解】6x-2.7=1.5
解:6x-2.7+2.7=1.5+2.7
6x=4.2
6x÷6=4.2÷6
x=0.7
8(x-1.6)=8.64
解:8(x-1.6)÷8=8.64÷8
x-1.6=1.08
x-1.6+1.6=1.08+1.6
x=2.68
7x-4.3×6=9.34
解:7x-25.8=9.34
7x-25.8+25.8=9.34+25.8
7x=35.14
7x÷7=35.14÷7
x=5.02
4x+1.6x=16.8
解:5.6x=16.8
5.6x÷5.6=16.8÷5.6
x=3
22.见详解
【分析】先化简方程,然后根据等式的性质,求出方程的解,再连线即可求解。
【详解】4x=8.8
解:4x÷4=8.8÷4
x=2.2
0.2x+0.4x=2.4
解:0.6x=2.4
0.6x÷0.6=2.4÷0.6
x=4
6x-0.9=4.5
解:6x-0.9+0.9=4.5+0.9
6x=5.4
6x÷6=5.4÷6
x=0.9
连线如下:
【点睛】本题也可以把x的值分别带入方程,找出能使方程左右两边相等的数。
23.20枚
【分析】根据“两种邮票的数量相同”,设面额为6角和8角的邮票各有枚;
根据“花了28元钱”可得出等量关系:面额6角的邮票×枚数+面额8角的邮票×枚数=一共花的钱数;据此列出方程,并求解。
注意单位的换算:1元=10角。
【详解】28元=280角
解:设面额为6角和8角的邮票各有枚。
6+8=280
14=280
14÷14=280÷14
=20
答:小红买的两种邮票各20枚。
【点睛】本题考查列方程解决问题,从题目中找到等量关系,按等量关系列出方程。
24.7岁
【分析】根据题意可得出等量关系:张芳今年的年龄×3-4=陈静今年的年龄,据此列出方程,并求出方程的解。
【详解】解:设张芳今年岁。
3-4=17
3-4+4=17+4
3=21
3÷3=21÷3
=7
答:张芳今年7岁。
【点睛】本题考查列方程解决问题,从题目中找到等量关系,按等量关系列出方程。
25.260种
【分析】先设湿地鸟类有x种,可以列出等量关系式为8x+178=2258.据此解答。
【详解】解:设湿地鸟类有x种。
8x+178=2258
8x+178-178=2258-178
8x=2080
8x÷8=2080÷8
x=260
答:湿地鸟类有260种。
【点睛】此题考查了学生对列方程、解方程的熟练掌握程度。关键是找出等量关系式。
26.5天
【分析】本题已知了第一队的工作天数和每天开凿的长度,即总长度=第一队每天开凿的长度×第一队需要开凿的天数+第二队每天开凿的长度×第二队需要开凿的天数,由此列出方程解答即可。
【详解】解:设剩下的第二队完成需要x天。
63+14.4x=135
63+14.4x-63=135-63
14.4x=72
14.4x÷14.4=72÷14.4
答:剩下的第二队完成需要5天。
【点睛】此题主要考查了工程问题的应用,对此类问题要注意把握住基本关系,即:工作量=工作效率×工作时间,工作效率=工作量÷工作时间,工作时间=工作量÷工作效率。
27.(1)55t千米;132千米;
(2)(230-55t)千米;43千米
【分析】(1)根据题意可知,汽车行驶的路程=汽车的速度×汽车行驶的时间,代入数据解答即可,再把t=2.4代入计算即可;
(2)根据题意可知,汽车离B城的距离=AB两地的总路程-汽车行驶的路程,代入数据解答即可,再把t=3.4代入计算即可。
【详解】(1)汽车离A城有55t千米远,
当t=2.4时,
55t
=55×2.4
=132(千米)
答:开出t小时后汽车离A城有55t千米远;如果t=2.4,汽车离开A城有32千米。
(2)汽车离B城有(230-55t)千米远,
当t=3.4时,
230-55t
=230-55×3.4
=230-187
=43(千米)
答:开出t小时后汽车离B城有(230-55t)千米远;如果t=3.4,汽车距离B城有43千米远。
28.快递员:6名;包裹:66件
【分析】可列方程解决盈亏问题。根据题意可知,无论按哪种派送方法,包裹的总件数是一定的。若每个快递员派送10件,还剩6件,则包裹的总件数是10×快递员的人数+6;若每个快递员派送12件,还差6件,则包裹的总件数是12×快递员的人数-6。所以此题的等量关系为“10×快递员的人数+6=12×快递员的人数-6”。设快递员x名,则可列出方程10x+6=12x-6,解方程即可求出快递员的人数;再用10×快递员的人数+6可求出包裹的件数。
【详解】解:设快递员x名。
10x+6=12x-6
10x+6+6=12x-6+6
10x+12=12x
10x+12-10x=12x-10x
12=2x
2x=12
2x÷2=12÷2
x=6
10×6+6
=60+6
=66(件)
答:该分派站现有包裹66件,快递员6名。
【点睛】此题考查了运用抓不变量法列方程解决盈亏问题。根据包裹的总件数不变建立等量关系是解答此题的关键。
29.(1)42个
(2)220名
【分析】(1)根据题意可知,乘车去博物馆参观的总人数一定,等量关系:每辆车可乘坐的人数×5+10=每辆车可乘坐的人数×6-32,据此列出方程,并求解。
(2)把上一题求出的每辆车可乘坐的人数代入方程左边或右边,即可求出总人数。
【详解】(1)解:设每辆车上有个座位。
5+10=6-32
5+10-5=6-32-5
10=-32
-32+32=10+32
=42
答:每辆车上有42个座位。
(2)5×42+10
=210+10
=220(名)
答:一共有220名同学去博物馆参观。
【点睛】本题考查列方程解决问题,从题目中找到等量关系,按等量关系列出方程。
30.20立方米
【分析】由题意得,设该用户一月份用水量为x,根据等量关系“水费=1.8×15+2.3×超出15立方米的部分+污水处理费”列出方程即可求解。
【详解】若某户每月用水量为15立方米,则需支付水费:
15×(1.8+1)
=15×2.8
=42(元)
42<58.5
即该户一月份用水量超过15立方米;
解:设该户一月份用水量为x立方米,根据题意得:
15×1.8+2.3(x-15)+x=58.5
27+(2.3x-34.5)+x=58.5
27+2.3x-34.5+x=58.5
27-34.5+(2.3x+x)=58.5
27-34.5+3.3x=58.5
27-34.5+3.3x+34.5=58.5+34.5
27+3.3x=93
27+3.3x-27=93-27
3.3x=66
3.3x÷3.3=66÷3.3
x=20
答:该户一月份用水量为20立方米。
【点睛】此题为解方程的应用题,同学们应学会运用方程解决实际问题的能力。
一、选择题(共16分)
1.郑州市动物园位于郑州市金水区花园路北段,是河南省唯一一座专业性动物园。周末苗苗到动物园参观,发现一片园区里养有单峰骆驼和双峰骆驼,她数了数共有36个头,48个驼峰,那么这个园区内共有( )头双峰骆驼。
A.24 B.12 C.18 D.6
2.数m、n、t按数值大小在直线上的位置如下,与数t最接近的是( )。
A.n×m B.n+m C.n÷m D.n-m
3.小正方形的边长是a厘米,大正方形的边长等于小正方形的周长,大正方形的面积是( )平方厘米。
A. B. C. D.
4.水果店运来15箱苹果和10箱橘子,其重1520kg。已知每箱苹果重25kg,求每箱橘子重多少千克。设每箱橘子重xkg,以下方程不能成立的是( )。
A. B.
C. D.
5.小明把5x+0.4错写成了5(x+0.4),结果比原来( )。
A.多0.4 B.少0.4 C.少1.6 D.多1.6
6.有m个馄饨(m为整十数),每碗装10个,可以装( )碗。
A. B. C. D.
7.福州西湖公园至今有一千七百多年的历史,是福州迄今为止保留最完整的一座古典园林,被称为“福建园林明珠”,现占地面积为42.51公顷,其中陆地面积是12.21公顷,水面面积是x公顷。根据其中的数量关系,下列方程正确的是( )。
A. B.
C. D.
8.小明把6(x+4)错写成了6x+4,结果比原来( )。
A.多20 B.多4 C.少20 D.少4
二、填空题(共16分)
9.服装厂的工人每人每天可以生产5件上衣或8条裤子,一件上衣和一条裤子为一套服装。现有104名工人,每天最多能生产( )套服装。
10.根据题意找出等量关系,并且列出方程。
张明买了4本练习本,每本x元,付给售货员10元,找回4元。( )
11.箱子里有同样数量的苹果和梨。小东每次从这个箱子里取出5个苹果和2个梨,取了几次后,苹果没有了,梨还剩18个。箱子里原来有( )个梨。
12.在括号里填上含有字母的式子。
(1)一辆卡车运x吨煤,共运了3次,平均每次运煤( )吨。
(2)五年级学生小丽和爸爸妈妈一起去公园,公园的成人门票是每张a元,学生门票是每张b元。小丽一家三口共需付( )元购买门票。
13.水果店运来a箱橘子,运来的苹果比橘子多5箱,运来苹果( )箱。当a=18时,水果店共运来( )箱水果。
14.定义新运算“ ”,A B=(A-2)×B,如果A 5=30,那么A=( )。
15.小红拿着x元钱买了单价为15元的大枣2千克,应找回( )元;若x=50,应找回( )元。
16.最新研究发现,真空管道中高速列车的时速(即每小时行的路程),比现在高铁时速的3倍还快150千米。高铁时速a千米,真空管道中高速列车的时速是( )千米。
三、判断题(共8分)
17.学校组织研学活动,租用大巴车和小巴车共8辆,大巴车每辆600元,小巴车每辆450元。如果租用的大巴车为a辆,那么租用小巴车的费用是450×(8-a)元。( )
18.有两个数和b,都大于1,两数相乘,它们的积比大。( )
19.甲数比乙数小6,如果甲数是a,则乙数是a-6。( )
20.如果数对(3,)和(,4)表示的位置在同一列,那么=3。( )
四、计算题(共6分)
21.解方程。
6x-2.7=1.5 8(x-1.6)=8.64
7x-4.3×6=9.34 4x+1.6x=16.8
五、连线题(共6分)
22.找出方程的解,连一连。
六、解答题(共48分)
23.小红花了28元钱买了面额为6角和8角的邮票。两种邮票的数量相同,小红买的两种邮票各多少枚?(用方程解)
24.算一算张芳今年多少岁?
25.截至2022年1月,我国的国际重要湿地生态状况总体保持稳定,其中湿地植物2258种,比湿地鸟类的8倍多178种。湿地鸟类有多少种?(先列出等量关系,再列方程解答)
26.两个工程队合作开凿一条长135米的隧道,各从一端开始。第一队每天开凿12.6米,第二队每天开凿14.4米。若第一队开凿5天后,剩下的第二队完成需要多少天?(列方程解)
27.A、B两城相距230千米,汽车从A城开往B城,每小时行驶55千米。
(1)开出t小时后汽车离A城有多远?如果t=2.4,汽车离开A城有多远?
(2)开出t小时后汽车离B城有多远?如果t=3.4,汽车距离B城有多远?
28.近年来,网购的蓬勃发展方便了人们的生活。某快递分派站现有包裹若干件需快递员派送。若每个快递员派送10件,还剩6件;若每个快递员派送12件,还差6件。该分派站现有包裹多少件?快递员多少名?
29.五年级同学乘车去博物馆参观。如果租5辆车,则有10名同学没有座位;如果租6辆车,则多出32个座位。
(1)每辆车上有多少个座位?(列方程解答)
(2)一共有多少名同学去博物馆参观?
30.某市为更有效地利用水资源,制定了居民用水收费标准:如果一户每月用水量不超过15立方米,每立方米按1.8元收费;如果超过15立方米,超过部分按每立方米2.3元收费。另外,每立方米加收污水处理费1元。若某户一月份共支付水费58.5元,求该户一月份用水量。
参考答案
1.B
【分析】设这个园区内共有x头双峰骆驼,则单峰骆驼有(36-x)头,单峰骆驼数量×1+双峰骆驼×2=48,据此列出方程求出x的值即可。
【详解】解:设这个园区内共有x头双峰骆驼。
(36-x)×1+2x=48
36-x+2x=48
36+x=48
36+x-36=48-36
x=12
这个园区内共有12头双峰骆驼。
故答案为:B
【点睛】本题考查鸡兔同笼问题,用方程解决问题的关键是找到等量关系。
2.C
【分析】看图,可以假设n为0.7,m为0.3,从而求出选项中式子的值。t在2和3之间,据此找出与数t最接近的式子。
【详解】令n=0.7,m=0.3,
A.n×m=0.7×0.3=0.21;
B.n+m=0.7+0.3=1;
C.n÷m=0.7÷0.3≈2.33;
D.n-m=0.7-0.3=0.4;
又因为t>2,所以与数t最接近的是n÷m。
故答案为:C
【点睛】本题考查了含有字母式子的求值,有一定计算能力是解题的关键。
3.D
【分析】正方形的周长=边长×4,代入字母表示出大正方形的边长,再代入正方形的面积公式:S=a2计算即可。
【详解】(厘米)
(平方厘米)
大正方形的面积是平方厘米。
故答案为:D。
【点睛】本题主要考查用字母表示数,熟记正方形周长、面积公式是解题的关键。
4.A
【分析】由题意可知,苹果的重量为15×25kg,橘子的重量为10xkg,再根据等量关系:苹果的重量+橘子的重量=1520、苹果的重量=1520-橘子的重量或橘子的重量=1520-苹果的重量,据此列方程即可。
【详解】A.因为橘子的重量≠橘子和苹果的总量+苹果的重量,所以不成立;
B.因为橘子和苹果的总量-苹果的重量=橘子的重量,则可列方程为:,该方程成立;
C.因为苹果的重量+橘子的重量=1520,则可列方程为:,该方程成立;
D.因为苹果的重量=1520-橘子的重量,则可列方程为:,该方程成立。
故答案为:A
【点睛】本题考查用方程解决实际问题,明确等量关系是解题的关键。
5.D
【分析】采用赋值法,假设x=4,将x=4分别代入5x+0.4和5(x+0.4),分别求值,再求差即可。
【详解】假设x=4
5x+0.4
=5×4+0.4
=20+0.4
=20.4
5(x+0.4)
=5×(4+0.4)
=5×4+5×0.4
=20+2
=22
22-20.4=1.6
小明把5x+0.4错写成了5(x+0.4),结果比原来多1.6。
故答案为:D
6.D
【分析】用馄饨的总数量除以每碗装馄饨的数量,即可求出可以装多少碗。
【详解】(m÷10)碗
有m个馄饨(m为整十数),每碗装10个,可以装(m÷10)碗。
故答案为:D
7.A
【分析】根据题意,可知陆地面积+水面面积=占地面积,据此列出方程为。据此选择即可。
【详解】根据其中的数量关系,下列方程正确的是。
故答案为:A
8.C
【分析】先算出6(x+4),展开可知比6x+4大,所以再减去6x+4,即可算出答案。
【详解】6(x+4)
=6x+6×4
=6x+24
6x+24-(6x+4)
=6x-6x+24-4
=20
所以结果比原来少20。
故答案为:C
9.320
【分析】要使每天生产的套装最多,必须使生产的上衣和裤子的数量相等,人员分工合理,据此设生产上衣的人数为x人,则生产裤子的人数为(104-x)人,据此列方程解答。
【详解】解:设生产上衣的人数为x人,则生产裤子的人数为(104-x)人。
5x=8×(104-x)
5x=8×104-8x
5x+8x=8×104-8x+8x
13x=832
13x÷13=832÷13
x=64
5×64=320(套)
则每天最多能生产320套服装。
10.4本练习本的钱数+找回的钱=10元;4+4x=10
【分析】根据题意可知,4本练习本的总价加上找回的钱等于付出的钱,根据总价=单价×数量,每本为x元,则4本是4x元,据此列方程解答。
【详解】等量关系:4本练习本的钱数+找回的钱=10元
列出的方程:4+4x=10
【点睛】此题考查了学生列方程的能力,找准等量关系是解题的关键。
11.30
【分析】根据“箱子里有同样数量的苹果和梨”可得等量关系:每次取出苹果的个数×取的次数=每次取出梨的个数×取的次数+梨还剩下的个数;据此列出方程,并求解。
【详解】解:设取了次。
5=2+18
5-2=2+18-2
3=18
3÷3=18÷3
=6
梨:
2×6+18
=12+18
=30(个)
箱子里原来有30个梨。
【点睛】本题考查列方程解决问题,从题目中找到等量关系,按等量关系列出方程。
12.(1)x÷3
(2)2a+b/b+2a
【分析】(1)将煤的总量x吨除以3次,表示出平均每次运煤多少吨;
(2)将2张成人票票价加上1张儿童票票价,表示出购买门票一共需要付多少元。
【详解】(1)一辆卡车运x吨煤,共运了3次,平均每次运煤(x÷3)吨。
(2)小丽一家三口共需付(2a+b)元购买门票。
【点睛】本题考查了用字母表示数,有一定抽象概括能力是解题的关键,同时要注意数字和字母相乘,中间的乘号省略,数字在前,字母在后。
13. a+5 41
【分析】根据题意可知,橘子的箱数+5箱=苹果的箱数,据此可知,运来的苹果有(a+5)箱,然后把a=18代入a+5计算即可。
【详解】据分析可知,运来的苹果有(a+5)箱;
当a=18时,
苹果:18+5=23(箱)
共:23+18=41(箱)
水果店运来a箱橘子,运来的苹果比橘子多5箱,运来苹果(a+5)箱。当a=18时,水果店共运来41箱水果。
【点睛】本题主要考查了用字母表示数以及含未知数式子的求值,找到相应的数量关系式是解答本题的关键。
14.8
【分析】这道题规定的运算本质是:运算符号前面的数减去2,再乘运算符号后面的数。据此由A 5=30,则有(A-2)×5=30。再解关于A的方程,可求出A的值。
【详解】(A-2)×5=30
解:(A-2)×5÷5=30÷5
A-2=6
A-2+2=6+2
A=8
【点睛】解答定义新运算,关键是要正确地理解新定义的算式含义,然后严格按照新定义的计算程序,将数值代入,转化为常规的四则运算算式进行计算。
15. x-30 20
【分析】根据总价=单价×数量,求出总价,再用x元减去总价,表示出应找回多少元。再把x=50代入式子,计算即可解答。
【详解】x-15×2=x-30
50-30=20(元)
所以,应找回(x-30)元;若x=50,应找回20元。
【点睛】本题考查了用字母表示数,有一定抽象概括能力是解题的关键。
16.3a+150
【分析】根据题意可得出数量关系:高铁的时速×3+150=真空管道中高速列车的时速,据此用含字母的式子表示真空管道中高速列车的时速。
【详解】a×3+150=(3a+150)千米
真空管道中高速列车的时速是(3a+150)千米。
17.√
【分析】根据题意,租用大巴车和小巴车共8辆,其中租用的大巴车为a辆,那么租用小巴车为(8-a)辆;根据“单价×数量=总价”可得出数量关系:租用每辆小巴车的价钱×租用小巴车的数量=租用小巴车的费用,据此用含字母的式子表示租用小巴车的费用。
【详解】每辆小巴车450元,租用小巴车(8-a)辆,那么租用小巴车的费用是450×(8-a)元。
原题说法正确。
故答案为:√
【点睛】本题考查用字母表示式子,根据单价、数量、总价之间的关系得出数量关系,按数量关系写出含字母的式子。
18.√
【分析】根据积与因数的关系可知:当一个数乘一个大于1的数,所得的积比这个数大。据此判断。
【详解】令a=1.1,b=2,
则:1.1×2=2.2
2.2>1.1
原题说法正确。
故答案为:√
【点睛】掌握积与因数的关系是解答的关键。
19.×
【分析】已知甲数比乙数小6,则甲数=乙数-6,甲数+6=乙数,所以如果甲数是a,则乙数是a+6。
【详解】甲数比乙数小6,如果甲数是a,则乙数是a+6。原题干说法错误。
故答案为:×
20.√
【分析】用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行。
数对(3,)表示在第3列第行,数对(,4)表示在第列第4行;如果(3,)和(,4)表示的位置在同一列,由此可得出的值。
【详解】如果数对(3,)和(,4)表示的位置在同一列,那么=3。
原题说法正确。
故答案为:√
21.x=0.7;x=2.68;
x=5.02;x=3
【分析】(1)根据等式的性质,在方程两边同时加上2.7,再同时除以6即可;
(2)根据等式的性质,在方程两边同时除以8,再同时加上1.6即可;
(3)把原方程化简为7x-25.8=9.34,再根据等式的性质,在方程两边同时加上25.8,最后再同时除以7即可;
(4)把原方程化简为5.6x=16.8,再根据等式的性质,在方程两边同时除以5.6即可。
【详解】6x-2.7=1.5
解:6x-2.7+2.7=1.5+2.7
6x=4.2
6x÷6=4.2÷6
x=0.7
8(x-1.6)=8.64
解:8(x-1.6)÷8=8.64÷8
x-1.6=1.08
x-1.6+1.6=1.08+1.6
x=2.68
7x-4.3×6=9.34
解:7x-25.8=9.34
7x-25.8+25.8=9.34+25.8
7x=35.14
7x÷7=35.14÷7
x=5.02
4x+1.6x=16.8
解:5.6x=16.8
5.6x÷5.6=16.8÷5.6
x=3
22.见详解
【分析】先化简方程,然后根据等式的性质,求出方程的解,再连线即可求解。
【详解】4x=8.8
解:4x÷4=8.8÷4
x=2.2
0.2x+0.4x=2.4
解:0.6x=2.4
0.6x÷0.6=2.4÷0.6
x=4
6x-0.9=4.5
解:6x-0.9+0.9=4.5+0.9
6x=5.4
6x÷6=5.4÷6
x=0.9
连线如下:
【点睛】本题也可以把x的值分别带入方程,找出能使方程左右两边相等的数。
23.20枚
【分析】根据“两种邮票的数量相同”,设面额为6角和8角的邮票各有枚;
根据“花了28元钱”可得出等量关系:面额6角的邮票×枚数+面额8角的邮票×枚数=一共花的钱数;据此列出方程,并求解。
注意单位的换算:1元=10角。
【详解】28元=280角
解:设面额为6角和8角的邮票各有枚。
6+8=280
14=280
14÷14=280÷14
=20
答:小红买的两种邮票各20枚。
【点睛】本题考查列方程解决问题,从题目中找到等量关系,按等量关系列出方程。
24.7岁
【分析】根据题意可得出等量关系:张芳今年的年龄×3-4=陈静今年的年龄,据此列出方程,并求出方程的解。
【详解】解:设张芳今年岁。
3-4=17
3-4+4=17+4
3=21
3÷3=21÷3
=7
答:张芳今年7岁。
【点睛】本题考查列方程解决问题,从题目中找到等量关系,按等量关系列出方程。
25.260种
【分析】先设湿地鸟类有x种,可以列出等量关系式为8x+178=2258.据此解答。
【详解】解:设湿地鸟类有x种。
8x+178=2258
8x+178-178=2258-178
8x=2080
8x÷8=2080÷8
x=260
答:湿地鸟类有260种。
【点睛】此题考查了学生对列方程、解方程的熟练掌握程度。关键是找出等量关系式。
26.5天
【分析】本题已知了第一队的工作天数和每天开凿的长度,即总长度=第一队每天开凿的长度×第一队需要开凿的天数+第二队每天开凿的长度×第二队需要开凿的天数,由此列出方程解答即可。
【详解】解:设剩下的第二队完成需要x天。
63+14.4x=135
63+14.4x-63=135-63
14.4x=72
14.4x÷14.4=72÷14.4
答:剩下的第二队完成需要5天。
【点睛】此题主要考查了工程问题的应用,对此类问题要注意把握住基本关系,即:工作量=工作效率×工作时间,工作效率=工作量÷工作时间,工作时间=工作量÷工作效率。
27.(1)55t千米;132千米;
(2)(230-55t)千米;43千米
【分析】(1)根据题意可知,汽车行驶的路程=汽车的速度×汽车行驶的时间,代入数据解答即可,再把t=2.4代入计算即可;
(2)根据题意可知,汽车离B城的距离=AB两地的总路程-汽车行驶的路程,代入数据解答即可,再把t=3.4代入计算即可。
【详解】(1)汽车离A城有55t千米远,
当t=2.4时,
55t
=55×2.4
=132(千米)
答:开出t小时后汽车离A城有55t千米远;如果t=2.4,汽车离开A城有32千米。
(2)汽车离B城有(230-55t)千米远,
当t=3.4时,
230-55t
=230-55×3.4
=230-187
=43(千米)
答:开出t小时后汽车离B城有(230-55t)千米远;如果t=3.4,汽车距离B城有43千米远。
28.快递员:6名;包裹:66件
【分析】可列方程解决盈亏问题。根据题意可知,无论按哪种派送方法,包裹的总件数是一定的。若每个快递员派送10件,还剩6件,则包裹的总件数是10×快递员的人数+6;若每个快递员派送12件,还差6件,则包裹的总件数是12×快递员的人数-6。所以此题的等量关系为“10×快递员的人数+6=12×快递员的人数-6”。设快递员x名,则可列出方程10x+6=12x-6,解方程即可求出快递员的人数;再用10×快递员的人数+6可求出包裹的件数。
【详解】解:设快递员x名。
10x+6=12x-6
10x+6+6=12x-6+6
10x+12=12x
10x+12-10x=12x-10x
12=2x
2x=12
2x÷2=12÷2
x=6
10×6+6
=60+6
=66(件)
答:该分派站现有包裹66件,快递员6名。
【点睛】此题考查了运用抓不变量法列方程解决盈亏问题。根据包裹的总件数不变建立等量关系是解答此题的关键。
29.(1)42个
(2)220名
【分析】(1)根据题意可知,乘车去博物馆参观的总人数一定,等量关系:每辆车可乘坐的人数×5+10=每辆车可乘坐的人数×6-32,据此列出方程,并求解。
(2)把上一题求出的每辆车可乘坐的人数代入方程左边或右边,即可求出总人数。
【详解】(1)解:设每辆车上有个座位。
5+10=6-32
5+10-5=6-32-5
10=-32
-32+32=10+32
=42
答:每辆车上有42个座位。
(2)5×42+10
=210+10
=220(名)
答:一共有220名同学去博物馆参观。
【点睛】本题考查列方程解决问题,从题目中找到等量关系,按等量关系列出方程。
30.20立方米
【分析】由题意得,设该用户一月份用水量为x,根据等量关系“水费=1.8×15+2.3×超出15立方米的部分+污水处理费”列出方程即可求解。
【详解】若某户每月用水量为15立方米,则需支付水费:
15×(1.8+1)
=15×2.8
=42(元)
42<58.5
即该户一月份用水量超过15立方米;
解:设该户一月份用水量为x立方米,根据题意得:
15×1.8+2.3(x-15)+x=58.5
27+(2.3x-34.5)+x=58.5
27+2.3x-34.5+x=58.5
27-34.5+(2.3x+x)=58.5
27-34.5+3.3x=58.5
27-34.5+3.3x+34.5=58.5+34.5
27+3.3x=93
27+3.3x-27=93-27
3.3x=66
3.3x÷3.3=66÷3.3
x=20
答:该户一月份用水量为20立方米。
【点睛】此题为解方程的应用题,同学们应学会运用方程解决实际问题的能力。
