苏科版八年级数学下册 9.3.1平行四边形的性质 试题(含答案)
文档属性
| 名称 | 苏科版八年级数学下册 9.3.1平行四边形的性质 试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 108.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 12:44:05 | ||
图片预览




文档简介
9.3.1平行四边形的性质
一、选择题.
1.如图所示,平行四边形ABCD中,AC=4cm,BD=6cm,则边AD的长可以是( )
A.4cm B.5cm C.6cm D.7cm
2.下列特征中,平行四边形不一定具有的是( )
A.邻角互补 B.对角互补
C.对角相等 D.内角和为360
3.如图,在 ABCD中,AD=11,AB=7,AE平分∠BAD,交BC边于点E,则CE的长为( )
A.7 B.6 C.4 D.2
4.在 ABCF中,BC=2AB,CD⊥AB于点D,点E为AF的中点,若∠ADE=50°.则∠B的度数是( )
A.50° B.60° C.70° D.80°
5.如图, ABCD中,∠A比∠D大40°,则∠C等于( )
A.70° B.100° C.110° D.120°
6.在 ABCD中,对角线AC、BD相交于点O,若∠ABC=90°,则下列结论错误的是( )
A.AC=BD B.OA=OB C.AC⊥BD D.AB=CD
7.如图,平行四边形ABCD的对角线交于点O,且AB=8,△OCD的周长为20,则平行四边形ABCD的两条对角线的和是( )
A.40 B.28 C.24 D.12
8.如图,在平面直角坐标系中, ABCD的顶点坐标分别为A(3,a),B(2,2),C(b,3),D(8,6),则a+b的值为( )
A.8 B.9 C.12 D.11
9.在 ABCD中,∠ABC的角平分线交线段AD于点E,DE=1,点F是BE中点,连接CF,过点F作FG⊥BC,垂足为G,设AB=x,若 ABCD的面积为8,FG的长为整数,则整数x的值为( )
A.1 B.2 C.3 D.2或3
10.如图,在四边形ABCD中,AD∥BC,AD=6cm,BC=12cm,点P从A出发以1cm/s的速度向D运动,点Q从C出发以2cm/s的速度向B运动,两点同时出发,当点P运动到点D时,点Q也随之停止运动.若运动时间为t秒时,以A、B、C、D、P、Q任意四个点为顶点的四边形中同时存在两个平行四边形,则t的值是( )
A.1 B.2 C.3 D.4
二、填空题
11. ABCD中,对角线AC和BD相交于O,如果AC=10,BD=6,AB=m,那么m的取值范围是 .
12.在 ABCD中,已知周长为44cm,AB比BC短2cm,则CD=
13.如图,在平行四边形ABCD中,AE平分∠BAD,交CD边于点E,AD=5,EC=3,则AB的长为 .
14.如图,平行四边形中,∠ADC=118°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,则∠BHF= 度.
15.如图,已知E为 ABCD内一点,且AD=DE=CE,若∠DEC=n°,则∠AEB的度数为 °.(用含n的代数式表示).
16.如图,平行四边形ABCD的对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE.若△ABE的周长为10cm,则平行四边形ABCD的周长为 cm.
17.如图,在△ABC中,AC,∠CAB=30°,D为AB上的动点,连接CD,以AD、CD为边作平行四边形ADCE,则DE长的最小值为 .
18.如图, ABCD中,对角线BD的垂直平分线交CD于点E,连接BE.若 ABCD的周长为20cm,则△BCE的周长为 cm.
三、解答题
19.如图,在 ABCD中,点E、F分别在AD、BC边上,且AE=CF.求证:BE∥FD.
20.如图,在 ABCD中,已知E、F分别为边AB、CD的中点.
(1)求证:△ADE≌△CBF;
(2)若AB=2,∠ADB=90°,求四边形BEDF的周长.
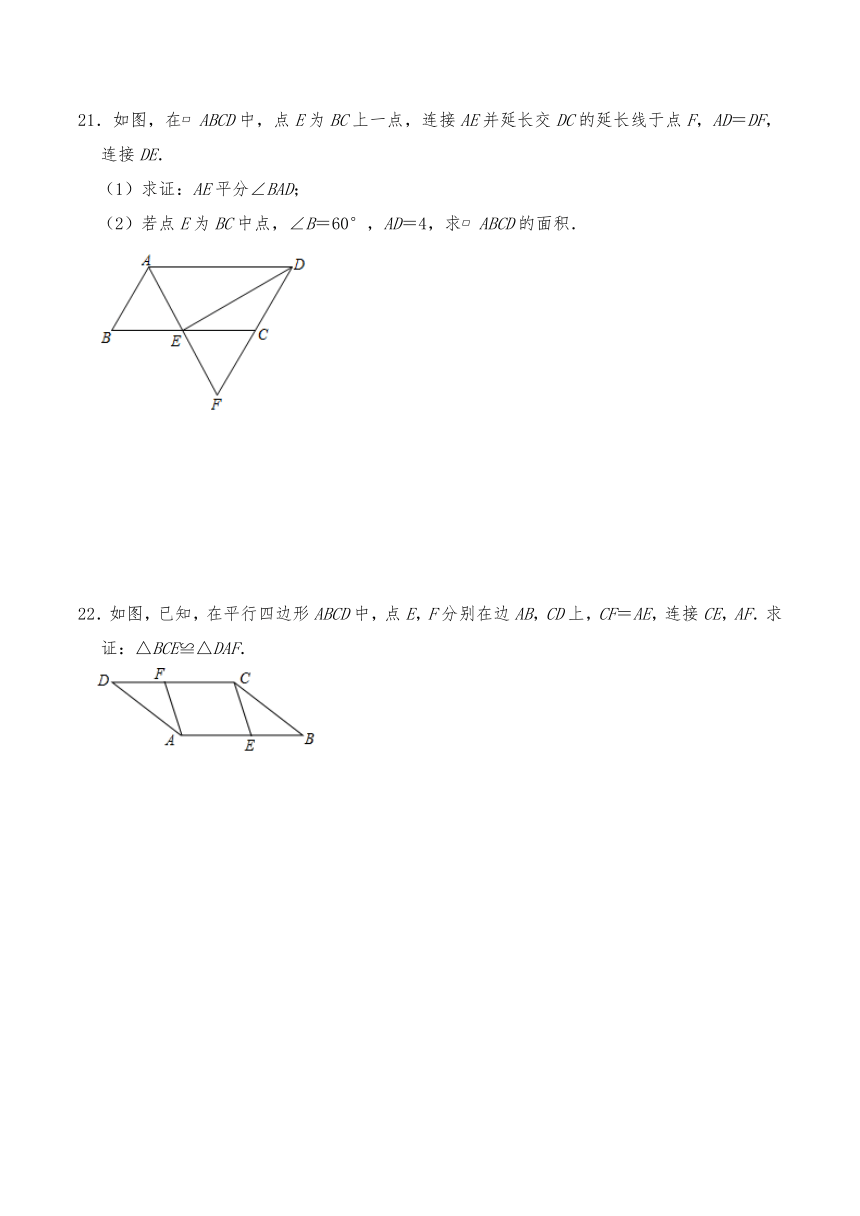
21.如图,在 ABCD中,点E为BC上一点,连接AE并延长交DC的延长线于点F,AD=DF,连接DE.
(1)求证:AE平分∠BAD;
(2)若点E为BC中点,∠B=60°,AD=4,求 ABCD的面积.
22.如图,已知,在平行四边形ABCD中,点E,F分别在边AB,CD上,CF=AE,连接CE,AF.求证:△BCE≌△DAF.
23.如图,平行四边形ABCD中,点E、F分别在边BC、AD上,EA⊥AC,FC⊥AC.
(1)求证:△ABE≌△CDF;
(2)若∠B=30°,∠AEC=45°,求证:AB=AF.
24.如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:△ABE≌△FCE;
(2)过点D作DG⊥AE于点G,H为DG的中点.判断CH与DG的位置关系,并说明理由.
答案
一、选择题.
A.B.C.D.C.C.C.C.C.C.
二、填空题
11.2<m<8.
12.10cm.
13.8.
14.62.
15.(180).
16.20.
17.2.
18.10.
三、解答题
19.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,DE∥BF,
∴四边形DEBF是平行四边形,
∴BE=DF.
20.证明:(1)在 ABCD中,∵AD=CB,AB=CD,∠A=∠C,
又∵E,F分别为边AB,CD的中点,
∴AE=CF,
在△ADE与△CBF中,
,
∴△ADE≌△CBF(SAS).
(2)∵∠ADB=90°,
∴△ABD,△CDB都是直角三角形,
∵AE=EB,CF=DF,
∴DE=BEAB,BF=DFCD,
∴DE=BE=BF=DF=1
∴四边形DEBF是菱形,周长为4.
21.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠BAE=∠AFD,
∵AD=DF,
∴∠DAE=∠AFD,
∴∠BAE=∠DAE,
即AE平分∠BAD;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥DF,AB=DC,AD=BC,
∵点E为BC中点,
∴BE=EC2,
∵AD=DF=4,
∴CD=AB=2,
∵∠B=60°,
∴BC边的高是,
∴ ABCD的面积=4.
22.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD=BC,
∴∠D=∠B,
∵CF=AE,
∴BE=DF,
在△AFD与△CEB中,
∴△BCE≌△DAF(SAS).
23.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,∠B=∠D,AD∥BC,
∴AF∥EC,
∵EA⊥AC,FC⊥AC,
∴EA∥FC,
∴四边形AECF是平行四边形.
∴EC=AF,
∴BE=BC﹣EC=AD﹣AF=DF,
∴在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)过点A作AG⊥EC于点G,如图所示:
∵EA⊥AC,∠AEC=45°,
∴△AEC为等腰直角三角形,
∵AG⊥EC,
∴AGECAF,
∵∠B=30°,
∴AGAB,
∴AFAB,
∴AB=AF.
24.(1)∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∴∠B=∠ECF
∵E为BC的中点,
∴BE=CE,
在△ABE和△FCE中,
∴△ABE≌△FCE.
(2)结论:CH⊥DG.理由如下:
∵△ABE≌△FCE,
∴AB=CF,
∵AB=CD,
∴DC=CF,
∵H为DG的中点,
∴CH∥FG
∵DG⊥AE,
∴CH⊥DG.
一、选择题.
1.如图所示,平行四边形ABCD中,AC=4cm,BD=6cm,则边AD的长可以是( )
A.4cm B.5cm C.6cm D.7cm
2.下列特征中,平行四边形不一定具有的是( )
A.邻角互补 B.对角互补
C.对角相等 D.内角和为360
3.如图,在 ABCD中,AD=11,AB=7,AE平分∠BAD,交BC边于点E,则CE的长为( )
A.7 B.6 C.4 D.2
4.在 ABCF中,BC=2AB,CD⊥AB于点D,点E为AF的中点,若∠ADE=50°.则∠B的度数是( )
A.50° B.60° C.70° D.80°
5.如图, ABCD中,∠A比∠D大40°,则∠C等于( )
A.70° B.100° C.110° D.120°
6.在 ABCD中,对角线AC、BD相交于点O,若∠ABC=90°,则下列结论错误的是( )
A.AC=BD B.OA=OB C.AC⊥BD D.AB=CD
7.如图,平行四边形ABCD的对角线交于点O,且AB=8,△OCD的周长为20,则平行四边形ABCD的两条对角线的和是( )
A.40 B.28 C.24 D.12
8.如图,在平面直角坐标系中, ABCD的顶点坐标分别为A(3,a),B(2,2),C(b,3),D(8,6),则a+b的值为( )
A.8 B.9 C.12 D.11
9.在 ABCD中,∠ABC的角平分线交线段AD于点E,DE=1,点F是BE中点,连接CF,过点F作FG⊥BC,垂足为G,设AB=x,若 ABCD的面积为8,FG的长为整数,则整数x的值为( )
A.1 B.2 C.3 D.2或3
10.如图,在四边形ABCD中,AD∥BC,AD=6cm,BC=12cm,点P从A出发以1cm/s的速度向D运动,点Q从C出发以2cm/s的速度向B运动,两点同时出发,当点P运动到点D时,点Q也随之停止运动.若运动时间为t秒时,以A、B、C、D、P、Q任意四个点为顶点的四边形中同时存在两个平行四边形,则t的值是( )
A.1 B.2 C.3 D.4
二、填空题
11. ABCD中,对角线AC和BD相交于O,如果AC=10,BD=6,AB=m,那么m的取值范围是 .
12.在 ABCD中,已知周长为44cm,AB比BC短2cm,则CD=
13.如图,在平行四边形ABCD中,AE平分∠BAD,交CD边于点E,AD=5,EC=3,则AB的长为 .
14.如图,平行四边形中,∠ADC=118°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,则∠BHF= 度.
15.如图,已知E为 ABCD内一点,且AD=DE=CE,若∠DEC=n°,则∠AEB的度数为 °.(用含n的代数式表示).
16.如图,平行四边形ABCD的对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE.若△ABE的周长为10cm,则平行四边形ABCD的周长为 cm.
17.如图,在△ABC中,AC,∠CAB=30°,D为AB上的动点,连接CD,以AD、CD为边作平行四边形ADCE,则DE长的最小值为 .
18.如图, ABCD中,对角线BD的垂直平分线交CD于点E,连接BE.若 ABCD的周长为20cm,则△BCE的周长为 cm.
三、解答题
19.如图,在 ABCD中,点E、F分别在AD、BC边上,且AE=CF.求证:BE∥FD.
20.如图,在 ABCD中,已知E、F分别为边AB、CD的中点.
(1)求证:△ADE≌△CBF;
(2)若AB=2,∠ADB=90°,求四边形BEDF的周长.
21.如图,在 ABCD中,点E为BC上一点,连接AE并延长交DC的延长线于点F,AD=DF,连接DE.
(1)求证:AE平分∠BAD;
(2)若点E为BC中点,∠B=60°,AD=4,求 ABCD的面积.
22.如图,已知,在平行四边形ABCD中,点E,F分别在边AB,CD上,CF=AE,连接CE,AF.求证:△BCE≌△DAF.
23.如图,平行四边形ABCD中,点E、F分别在边BC、AD上,EA⊥AC,FC⊥AC.
(1)求证:△ABE≌△CDF;
(2)若∠B=30°,∠AEC=45°,求证:AB=AF.
24.如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:△ABE≌△FCE;
(2)过点D作DG⊥AE于点G,H为DG的中点.判断CH与DG的位置关系,并说明理由.
答案
一、选择题.
A.B.C.D.C.C.C.C.C.C.
二、填空题
11.2<m<8.
12.10cm.
13.8.
14.62.
15.(180).
16.20.
17.2.
18.10.
三、解答题
19.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,DE∥BF,
∴四边形DEBF是平行四边形,
∴BE=DF.
20.证明:(1)在 ABCD中,∵AD=CB,AB=CD,∠A=∠C,
又∵E,F分别为边AB,CD的中点,
∴AE=CF,
在△ADE与△CBF中,
,
∴△ADE≌△CBF(SAS).
(2)∵∠ADB=90°,
∴△ABD,△CDB都是直角三角形,
∵AE=EB,CF=DF,
∴DE=BEAB,BF=DFCD,
∴DE=BE=BF=DF=1
∴四边形DEBF是菱形,周长为4.
21.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠BAE=∠AFD,
∵AD=DF,
∴∠DAE=∠AFD,
∴∠BAE=∠DAE,
即AE平分∠BAD;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥DF,AB=DC,AD=BC,
∵点E为BC中点,
∴BE=EC2,
∵AD=DF=4,
∴CD=AB=2,
∵∠B=60°,
∴BC边的高是,
∴ ABCD的面积=4.
22.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD=BC,
∴∠D=∠B,
∵CF=AE,
∴BE=DF,
在△AFD与△CEB中,
∴△BCE≌△DAF(SAS).
23.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,∠B=∠D,AD∥BC,
∴AF∥EC,
∵EA⊥AC,FC⊥AC,
∴EA∥FC,
∴四边形AECF是平行四边形.
∴EC=AF,
∴BE=BC﹣EC=AD﹣AF=DF,
∴在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)过点A作AG⊥EC于点G,如图所示:
∵EA⊥AC,∠AEC=45°,
∴△AEC为等腰直角三角形,
∵AG⊥EC,
∴AGECAF,
∵∠B=30°,
∴AGAB,
∴AFAB,
∴AB=AF.
24.(1)∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∴∠B=∠ECF
∵E为BC的中点,
∴BE=CE,
在△ABE和△FCE中,
∴△ABE≌△FCE.
(2)结论:CH⊥DG.理由如下:
∵△ABE≌△FCE,
∴AB=CF,
∵AB=CD,
∴DC=CF,
∵H为DG的中点,
∴CH∥FG
∵DG⊥AE,
∴CH⊥DG.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
