第五章 圆培优专题 圆与多边形同步练习(含答案)
文档属性
| 名称 | 第五章 圆培优专题 圆与多边形同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 9.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 11:44:42 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
培优专题
圆与多边形
类型一:圆与平行四边形
1.如图,在平行四边形 ABCO中, 点A,B在⊙O 上,点 D 在优弧ADB 上, DB,则 的度数为___________.
2.如图,AB 是半圆的直径,C 为半圆上一点,连接AC,BC,D为弧BC 上一点.连接OD,交 BC于点E,连接AE,若四边形ACDE 为平行四边形, 则AB的长为_________.
类型二:圆与正六边形
3.如图,⊙O 与正六边形ABCDEF 的两边AB和EF 分别相切于点B 和点E,若正六边形的边长是 则⊙O的半径长是( )
A.1 B. C.2 D.3
4.[创新意识]阅读理解:如图①,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点 M 的位置可由∠MOx 的度数θ与OM的长度 m 确定,有序数对(θ,m)称为 M 点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图②的极坐标系下,如果正六边形的边长为2,有一边OA 在射线Ox上,那么正六边形的顶点C 的极坐标应记为( )
类型三:圆与矩形
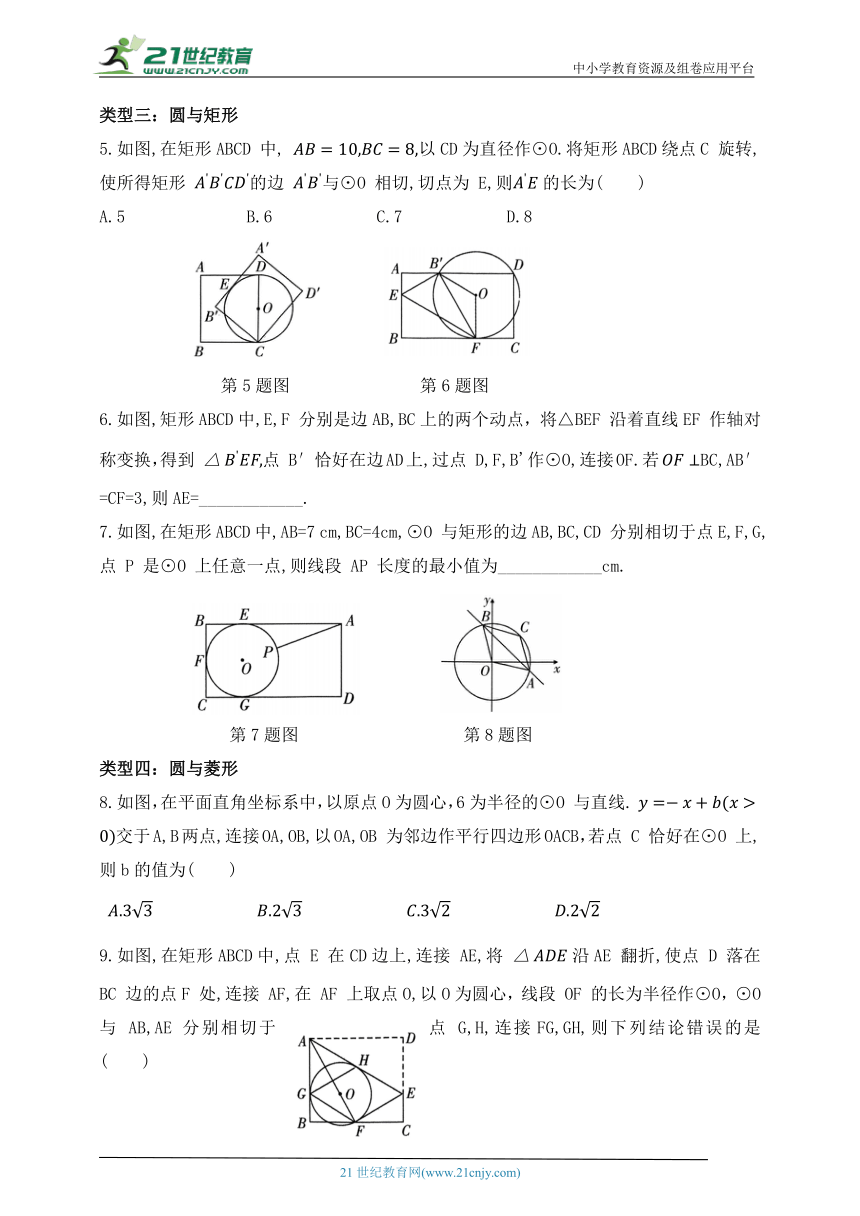
5.如图,在矩形ABCD 中, 以CD为直径作⊙O.将矩形ABCD绕点C 旋转,使所得矩形 的边 与⊙O 相切,切点为 E,则的长为( )
A.5 B.6 C.7 D.8
第5题图 第6题图
6.如图,矩形ABCD中,E,F 分别是边AB,BC上的两个动点,将△BEF 沿着直线EF 作轴对称变换,得到 点 B′恰好在边AD上,过点 D,F,B'作⊙O,连接OF.若BC,AB′=CF=3,则AE=____________.
7.如图,在矩形ABCD中,AB=7 cm,BC=4cm,⊙O 与矩形的边AB,BC,CD 分别相切于点E,F,G,点 P 是⊙O 上任意一点,则线段 AP 长度的最小值为____________cm.
第7题图 第8题图
类型四:圆与菱形
8.如图,在平面直角坐标系中,以原点O为圆心,6为半径的⊙O 与直线. 交于A,B两点,连接OA,OB,以OA,OB 为邻边作平行四边形OACB,若点 C 恰好在⊙O 上,则b的值为( )
9.如图,在矩形ABCD中,点 E 在CD边上,连接 AE,将 沿AE 翻折,使点 D 落在BC 边的点F 处,连接 AF,在 AF 上取点O,以O为圆心,线段 OF 的长为半径作⊙O,⊙O 与 AB,AE 分别相切于点 G,H,连接FG,GH,则下列结论错误的是( )
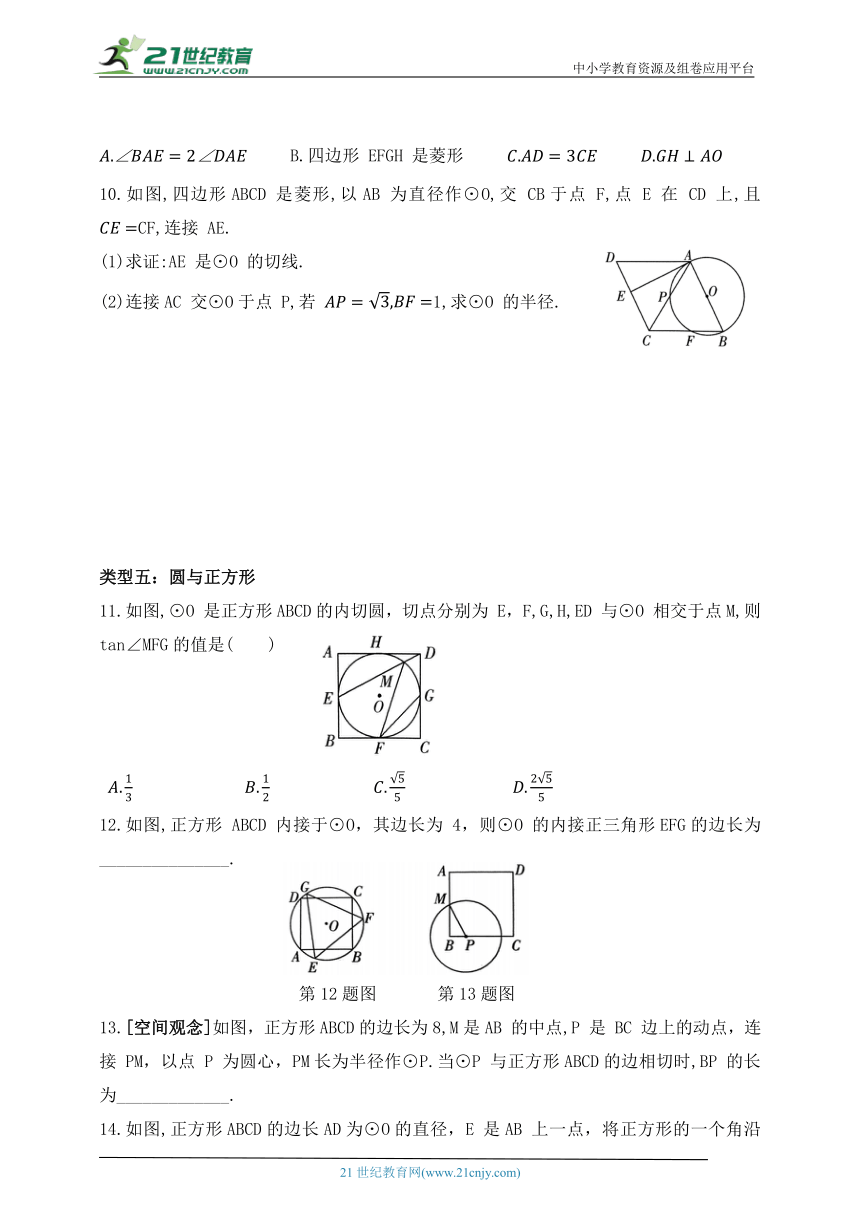
B.四边形 EFGH 是菱形
10.如图,四边形ABCD 是菱形,以AB 为直径作⊙O,交 CB于点 F,点 E 在 CD 上,且 CF,连接 AE.
(1)求证:AE 是⊙O 的切线.
(2)连接AC 交⊙O于点 P,若 1,求⊙O 的半径.
类型五:圆与正方形
11.如图,⊙O 是正方形ABCD的内切圆,切点分别为 E,F,G,H,ED 与⊙O 相交于点M,则 tan∠MFG的值是( )
12.如图,正方形 ABCD 内接于⊙O,其边长为 4,则⊙O 的内接正三角形EFG的边长为_______________.
第12题图 第13题图
13.[空间观念]如图,正方形ABCD的边长为8,M是AB 的中点,P 是 BC 边上的动点,连接 PM,以点 P 为圆心,PM长为半径作⊙P.当⊙P 与正方形ABCD的边相切时,BP 的长为_____________.
14.如图,正方形ABCD的边长AD为⊙O的直径,E 是AB 上一点,将正方形的一个角沿EC 折叠,使得点 B 恰好与圆上的点 F重合.
(1)求证:CF 与⊙O 相切.
(2)若⊙O的半径为 1,求 AE 的长.
参考答案
1.150°
2.6 [解析]如图,连接OC.∵AB 是直径,∴∠ACB=90°.∵四边形 ACDE 是平行四边形,∴AC=DE,CD=AE,AC∥DE,∴∠ACE=∠DEC=90°,∴OD⊥BC,∴EC= 负值舍去),∴AB=6.
3. C [解析]如图,连接OB,OE,BE.∵⊙O 与正六边形ABCDEF 的两边 AB 和EF 分别相切于点 B 和点 E,∴∠ABO=∠FEO =90°.∵∠BAF =∠EFA =120°,∴∠BOE=540°-120°-120°-90°-90°=120°,∴∠OBE=∠OEB=30°,∴∠ABE=∠FEB =60°,∴∠ABE+∠BAF=180°,∴AF∥BE.过点 A 作AM⊥BE于点M,FN⊥BE 于点 N,则四边形AMNF 是矩形,∴MN=AF过点 O 作OH⊥BE 于点 H,则∠OHB =90°,BH= ,∴OB=
4. A
5. B [解析]如图,连接OE,作 于点 H,则∵矩形 ABCD 绕点C 旋转所得矩形为A′B′CD′,∴∠B′=∠B′CD′=90°,AB=CD=10,BC=B′C=8,∴四边形OEB′H 是矩形,OE=OD=OC=5,∴B′H=OE=5,∴CH=B′C-B′H=3,∴B′E=OH则A′E=A′B′-B′E=10=4=6.
[解析]如图,延长FO交AD 于点 J,设AE=x.∵四边形ABCD是矩形,∴∠D=∠C=∠A=∠B=90°,AD∥CB,AD=BC.∵OF⊥BC,∴FJ⊥AD,∴∠AJF=∠FJD=90°,∴四边形ABFJ 是矩形,四边形CDJF 是矩形,∴AB=FJ=CD,CF=DJ=3.∵OJ⊥DB′,∴DJ=JB′=3,∴AD=BC=3+3+3=9,∴BF=BC-CF=6.由翻折的性质可知 在 中,有
[解析]如图,连接OF,OE,OG,AO,AO 交⊙O于点P,此时线段AP 长度最小.∵⊙O 与矩形的边AB,BC,CD分别相切于点E,F,G,∴OE⊥AB,OF⊥BC,OG⊥CD.∵AB∥CD,∴O,E,G三点共线,即 EG 为⊙O的直径,∴四边形 BCGE 为矩形,∴EG=BC=4cm.∵OE=OF=2cm,∴四边形BFOE 为正方形,∴BE=OF=2cm,∴AE = AB - BE = 5cm . 在 Rt△AEO 中,AO=2) cm,∴线段 AP长度的最小值为
8. C [解析]如图,连接OC 交AB于点T,设直线 AB交x轴于点M,交 y轴于点 N.
∵直线 AB的解析式为y=-x+b,∴N(0,b),M(b,0),∴OM=ON,∴∠OMN=45°.
∵四边形 OACB 是平行四边形,OA =OB,∴四边形OACB是菱形,∴OC⊥AB,∴∠COM=45°.∵OC=6,把 T 点坐标代入y=-x+b,可得
9. C [解析]由折叠可得:∠DAE=∠FAE,∠D=∠AFE=90°,EF=ED.∵AB 和AE 都是⊙O 的切线,点 G,H分别是切点,∴AG=AH,∠GAF=∠HAF,∴∠GAF=∠HAF=∠DAE=30°,∴∠BAE=2∠DAE,故 A 正确.如图,分别延长EF,AB 交于点N.∵OF⊥EF,OF 是⊙O的半径,∴EF 是⊙O 的切线,∴HE=EF,NF=NG,∴△ANE 是等边三角形,∴FG∥HE,FG=HE,∠AEF=60°,∴四边形 EFGH 是平行四边形,∠FEC=60°.又∵HE=EF,∴四边形EFGH 是菱形,故 B正确.∵AG=AH,∠GAF =∠HAF,∴GH⊥AO,故 D 正确.在Rt△EFC中,∠C=90°,∠FEC=60°,∴∠EFC=30°,∴EF=2CE,∴DE =2CE.∵∠AED=60°,∴AD=DE,∴AD=2 CE,故C错误.
(1)证明:如图,连接 AF.∵四边形 ABCD 为菱形,∴∠ACF = ∠ACE.
在△ACF与△ACE中, =∠AEC.∵AB 是⊙O 的直径,∴∠AFB=∠AFC=90°,∴∠AEC=90°.∵AB∥DC,∴∠BAE+∠AEC=180°,∴∠BAE=90°,∴OA⊥AE.∵OA 是⊙O 的半径,∴AE 是⊙O 的切线. (2)解:如图,连接 BP.∵AB 是⊙O 的直径,. 设⊙O的半径为 (负值舍去),∴⊙O的半径为
11. B [解析]如图,连接EG.∵E,G 是切点,∴EG 过点O.∵⊙O是正方形ABCD 的内切圆, BC=CD.根据圆周角的性质可得:∠MFG=∠MEG,
13.3或
14.(1)证明:如图,连接 OC,OF,则( ∵四边形ABCD 是正方形,. ∵将正方形的一个角沿EC折叠,使得点 B 恰好与圆上的点F重合, ∠ADC=90°,∴CF 与⊙O 相切.
(2)解:由(1)知∴O,F,E 三点共线.∵四边形ABCD是正方形, 设 则 :
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
培优专题
圆与多边形
类型一:圆与平行四边形
1.如图,在平行四边形 ABCO中, 点A,B在⊙O 上,点 D 在优弧ADB 上, DB,则 的度数为___________.
2.如图,AB 是半圆的直径,C 为半圆上一点,连接AC,BC,D为弧BC 上一点.连接OD,交 BC于点E,连接AE,若四边形ACDE 为平行四边形, 则AB的长为_________.
类型二:圆与正六边形
3.如图,⊙O 与正六边形ABCDEF 的两边AB和EF 分别相切于点B 和点E,若正六边形的边长是 则⊙O的半径长是( )
A.1 B. C.2 D.3
4.[创新意识]阅读理解:如图①,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点 M 的位置可由∠MOx 的度数θ与OM的长度 m 确定,有序数对(θ,m)称为 M 点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图②的极坐标系下,如果正六边形的边长为2,有一边OA 在射线Ox上,那么正六边形的顶点C 的极坐标应记为( )
类型三:圆与矩形
5.如图,在矩形ABCD 中, 以CD为直径作⊙O.将矩形ABCD绕点C 旋转,使所得矩形 的边 与⊙O 相切,切点为 E,则的长为( )
A.5 B.6 C.7 D.8
第5题图 第6题图
6.如图,矩形ABCD中,E,F 分别是边AB,BC上的两个动点,将△BEF 沿着直线EF 作轴对称变换,得到 点 B′恰好在边AD上,过点 D,F,B'作⊙O,连接OF.若BC,AB′=CF=3,则AE=____________.
7.如图,在矩形ABCD中,AB=7 cm,BC=4cm,⊙O 与矩形的边AB,BC,CD 分别相切于点E,F,G,点 P 是⊙O 上任意一点,则线段 AP 长度的最小值为____________cm.
第7题图 第8题图
类型四:圆与菱形
8.如图,在平面直角坐标系中,以原点O为圆心,6为半径的⊙O 与直线. 交于A,B两点,连接OA,OB,以OA,OB 为邻边作平行四边形OACB,若点 C 恰好在⊙O 上,则b的值为( )
9.如图,在矩形ABCD中,点 E 在CD边上,连接 AE,将 沿AE 翻折,使点 D 落在BC 边的点F 处,连接 AF,在 AF 上取点O,以O为圆心,线段 OF 的长为半径作⊙O,⊙O 与 AB,AE 分别相切于点 G,H,连接FG,GH,则下列结论错误的是( )
B.四边形 EFGH 是菱形
10.如图,四边形ABCD 是菱形,以AB 为直径作⊙O,交 CB于点 F,点 E 在 CD 上,且 CF,连接 AE.
(1)求证:AE 是⊙O 的切线.
(2)连接AC 交⊙O于点 P,若 1,求⊙O 的半径.
类型五:圆与正方形
11.如图,⊙O 是正方形ABCD的内切圆,切点分别为 E,F,G,H,ED 与⊙O 相交于点M,则 tan∠MFG的值是( )
12.如图,正方形 ABCD 内接于⊙O,其边长为 4,则⊙O 的内接正三角形EFG的边长为_______________.
第12题图 第13题图
13.[空间观念]如图,正方形ABCD的边长为8,M是AB 的中点,P 是 BC 边上的动点,连接 PM,以点 P 为圆心,PM长为半径作⊙P.当⊙P 与正方形ABCD的边相切时,BP 的长为_____________.
14.如图,正方形ABCD的边长AD为⊙O的直径,E 是AB 上一点,将正方形的一个角沿EC 折叠,使得点 B 恰好与圆上的点 F重合.
(1)求证:CF 与⊙O 相切.
(2)若⊙O的半径为 1,求 AE 的长.
参考答案
1.150°
2.6 [解析]如图,连接OC.∵AB 是直径,∴∠ACB=90°.∵四边形 ACDE 是平行四边形,∴AC=DE,CD=AE,AC∥DE,∴∠ACE=∠DEC=90°,∴OD⊥BC,∴EC= 负值舍去),∴AB=6.
3. C [解析]如图,连接OB,OE,BE.∵⊙O 与正六边形ABCDEF 的两边 AB 和EF 分别相切于点 B 和点 E,∴∠ABO=∠FEO =90°.∵∠BAF =∠EFA =120°,∴∠BOE=540°-120°-120°-90°-90°=120°,∴∠OBE=∠OEB=30°,∴∠ABE=∠FEB =60°,∴∠ABE+∠BAF=180°,∴AF∥BE.过点 A 作AM⊥BE于点M,FN⊥BE 于点 N,则四边形AMNF 是矩形,∴MN=AF过点 O 作OH⊥BE 于点 H,则∠OHB =90°,BH= ,∴OB=
4. A
5. B [解析]如图,连接OE,作 于点 H,则∵矩形 ABCD 绕点C 旋转所得矩形为A′B′CD′,∴∠B′=∠B′CD′=90°,AB=CD=10,BC=B′C=8,∴四边形OEB′H 是矩形,OE=OD=OC=5,∴B′H=OE=5,∴CH=B′C-B′H=3,∴B′E=OH则A′E=A′B′-B′E=10=4=6.
[解析]如图,延长FO交AD 于点 J,设AE=x.∵四边形ABCD是矩形,∴∠D=∠C=∠A=∠B=90°,AD∥CB,AD=BC.∵OF⊥BC,∴FJ⊥AD,∴∠AJF=∠FJD=90°,∴四边形ABFJ 是矩形,四边形CDJF 是矩形,∴AB=FJ=CD,CF=DJ=3.∵OJ⊥DB′,∴DJ=JB′=3,∴AD=BC=3+3+3=9,∴BF=BC-CF=6.由翻折的性质可知 在 中,有
[解析]如图,连接OF,OE,OG,AO,AO 交⊙O于点P,此时线段AP 长度最小.∵⊙O 与矩形的边AB,BC,CD分别相切于点E,F,G,∴OE⊥AB,OF⊥BC,OG⊥CD.∵AB∥CD,∴O,E,G三点共线,即 EG 为⊙O的直径,∴四边形 BCGE 为矩形,∴EG=BC=4cm.∵OE=OF=2cm,∴四边形BFOE 为正方形,∴BE=OF=2cm,∴AE = AB - BE = 5cm . 在 Rt△AEO 中,AO=2) cm,∴线段 AP长度的最小值为
8. C [解析]如图,连接OC 交AB于点T,设直线 AB交x轴于点M,交 y轴于点 N.
∵直线 AB的解析式为y=-x+b,∴N(0,b),M(b,0),∴OM=ON,∴∠OMN=45°.
∵四边形 OACB 是平行四边形,OA =OB,∴四边形OACB是菱形,∴OC⊥AB,∴∠COM=45°.∵OC=6,把 T 点坐标代入y=-x+b,可得
9. C [解析]由折叠可得:∠DAE=∠FAE,∠D=∠AFE=90°,EF=ED.∵AB 和AE 都是⊙O 的切线,点 G,H分别是切点,∴AG=AH,∠GAF=∠HAF,∴∠GAF=∠HAF=∠DAE=30°,∴∠BAE=2∠DAE,故 A 正确.如图,分别延长EF,AB 交于点N.∵OF⊥EF,OF 是⊙O的半径,∴EF 是⊙O 的切线,∴HE=EF,NF=NG,∴△ANE 是等边三角形,∴FG∥HE,FG=HE,∠AEF=60°,∴四边形 EFGH 是平行四边形,∠FEC=60°.又∵HE=EF,∴四边形EFGH 是菱形,故 B正确.∵AG=AH,∠GAF =∠HAF,∴GH⊥AO,故 D 正确.在Rt△EFC中,∠C=90°,∠FEC=60°,∴∠EFC=30°,∴EF=2CE,∴DE =2CE.∵∠AED=60°,∴AD=DE,∴AD=2 CE,故C错误.
(1)证明:如图,连接 AF.∵四边形 ABCD 为菱形,∴∠ACF = ∠ACE.
在△ACF与△ACE中, =∠AEC.∵AB 是⊙O 的直径,∴∠AFB=∠AFC=90°,∴∠AEC=90°.∵AB∥DC,∴∠BAE+∠AEC=180°,∴∠BAE=90°,∴OA⊥AE.∵OA 是⊙O 的半径,∴AE 是⊙O 的切线. (2)解:如图,连接 BP.∵AB 是⊙O 的直径,. 设⊙O的半径为 (负值舍去),∴⊙O的半径为
11. B [解析]如图,连接EG.∵E,G 是切点,∴EG 过点O.∵⊙O是正方形ABCD 的内切圆, BC=CD.根据圆周角的性质可得:∠MFG=∠MEG,
13.3或
14.(1)证明:如图,连接 OC,OF,则( ∵四边形ABCD 是正方形,. ∵将正方形的一个角沿EC折叠,使得点 B 恰好与圆上的点F重合, ∠ADC=90°,∴CF 与⊙O 相切.
(2)解:由(1)知∴O,F,E 三点共线.∵四边形ABCD是正方形, 设 则 :
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
