5.9 弧长及扇形的面积同步练习(含答案)
文档属性
| 名称 | 5.9 弧长及扇形的面积同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 11:42:35 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章 圆
9 弧长及扇形的面积
基础闯关
知识点一:弧长公式及应用
1.如图,折扇的骨柄长为 27 cm,折扇张开的角度为图中 的长为___________cm.(结果保留π)
2.如图,已知 AB 是⊙O的一条直径,延长AB 至C点,使 CD 与⊙O 相切于 D 点.若 则劣弧AD 的长为___________.
3.在如图所示的正方形网格中,O,A,B,C,D均是网格线交点,若 与 所在圆的圆心都为点O,则 与 的长度之比为_____________.
知识点二:扇形面积公式及应用
4.如图,一扇形纸扇完全打开后,外侧两竹条AB 和AC 的夹角为 长均为 25cm,贴纸部分的宽 BD 为 15 cm,若纸扇两面贴纸,则贴纸的面积为( )
5.[一题多辨](1)如图①,在半径为 6 的⊙O中,点A,B,C 都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )
A.6π D.2π
(2)如图②,扇形纸片 AOB 的半径为 2,沿AB 折叠扇形纸片,点 O 恰好落在 上的点C 处,则图中阴影部分的面积为___________.
知识点三:求弓形的面积
6.如图,内接于⊙O,若∠A=⊙O的半径为 4,则阴影部分的面积为( )
A.4π-8 B.2π C.4π D.8π-8
7.[几何直观]如图,在 的正方形网格中有一半径为5 的圆,一条折线将它分成甲、乙两部分. S甲表示甲的面积,则
知识点四:求阴影部分的面积
8.如图,在 Rt△ABC中,. 以 BC 为直径作半圆,交AB 于点D,则阴影部分的面积是( )
A.π-1 D.2
9.如图, 中, AB 与⊙O 相切于点C,则图中阴影部分的面积为_____________.(结果保留π)
10.如图,在平行四边形中, 以点A 为圆心,AD 的长为半径画弧交AB 于点E,连接CE,则图中阴影部分的面积是____________.(结果保留π)
能力提升
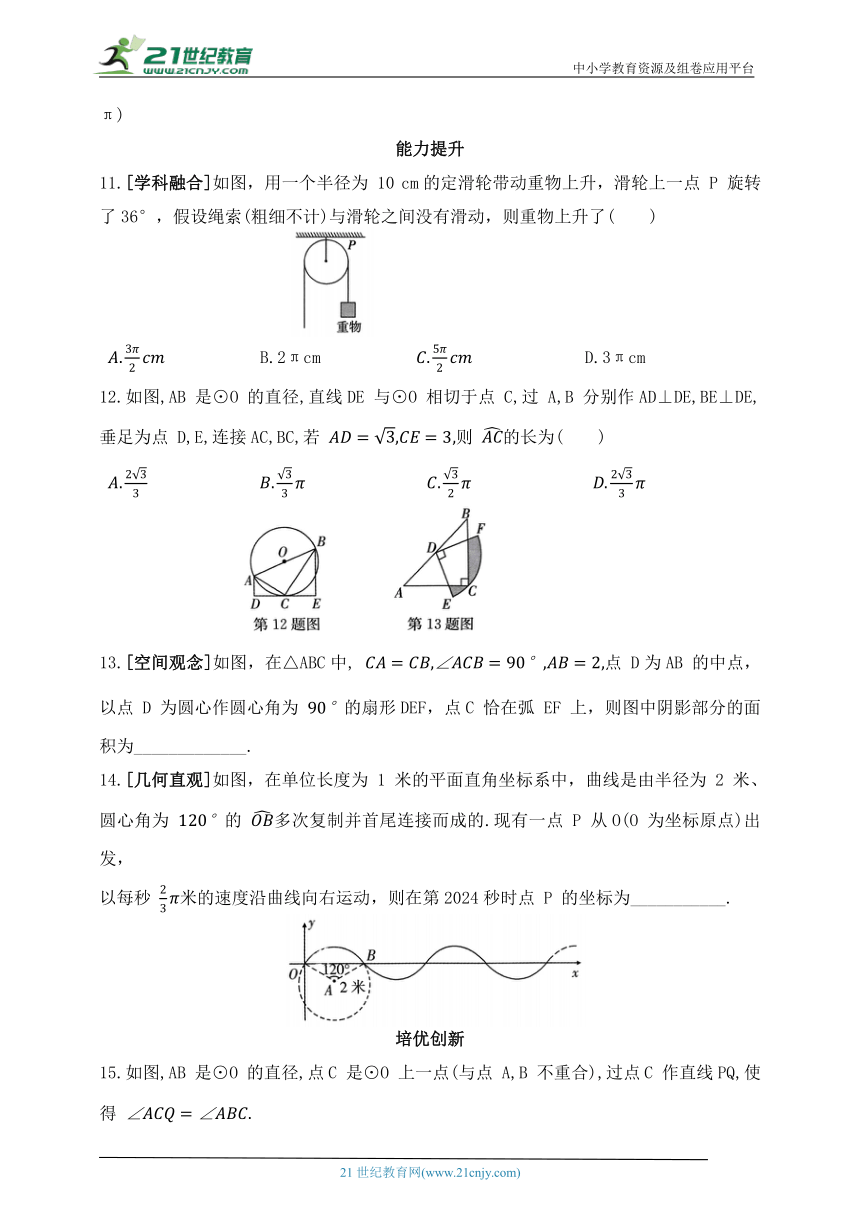
11.[学科融合]如图,用一个半径为 10 cm的定滑轮带动重物上升,滑轮上一点 P 旋转了36°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
B.2πcm D.3πcm
12.如图,AB 是⊙O 的直径,直线DE 与⊙O 相切于点 C,过 A,B 分别作AD⊥DE,BE⊥DE,垂足为点 D,E,连接AC,BC,若 则 的长为( )
13.[空间观念]如图,在△ABC中, 点 D为AB 的中点,以点 D 为圆心作圆心角为 的扇形DEF,点C 恰在弧 EF 上,则图中阴影部分的面积为_____________.
14.[几何直观]如图,在单位长度为 1 米的平面直角坐标系中,曲线是由半径为 2 米、圆心角为 的 多次复制并首尾连接而成的.现有一点 P 从O(O 为坐标原点)出发,
以每秒 米的速度沿曲线向右运动,则在第2024秒时点 P 的坐标为___________.
培优创新
15.如图,AB 是⊙O 的直径,点C 是⊙O 上一点(与点 A,B 不重合),过点C 作直线PQ,使得
(1)求证:直线 PQ 是⊙O 的切线.
(2)过点 A 作 于点 D,交⊙O 于点E,若⊙O的半径为 2, 求图
中阴影部分的面积.
参考答案
1.18π 4. B 5.(1)A 6. A
8. D 11. B 12. D
[解析]过点A 作 垂足为C,则在 中, 米, (米), 米, 的长为 (米), (米),∴点 P 的坐标为
15.(1)证明:连接OC.∵AB 是⊙O的直径,∴即∴直线 PQ 是⊙O 的切线.
(2)解:连接OE. 又为等边三角形, ∴图中阴影部分的面积为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
9 弧长及扇形的面积
基础闯关
知识点一:弧长公式及应用
1.如图,折扇的骨柄长为 27 cm,折扇张开的角度为图中 的长为___________cm.(结果保留π)
2.如图,已知 AB 是⊙O的一条直径,延长AB 至C点,使 CD 与⊙O 相切于 D 点.若 则劣弧AD 的长为___________.
3.在如图所示的正方形网格中,O,A,B,C,D均是网格线交点,若 与 所在圆的圆心都为点O,则 与 的长度之比为_____________.
知识点二:扇形面积公式及应用
4.如图,一扇形纸扇完全打开后,外侧两竹条AB 和AC 的夹角为 长均为 25cm,贴纸部分的宽 BD 为 15 cm,若纸扇两面贴纸,则贴纸的面积为( )
5.[一题多辨](1)如图①,在半径为 6 的⊙O中,点A,B,C 都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )
A.6π D.2π
(2)如图②,扇形纸片 AOB 的半径为 2,沿AB 折叠扇形纸片,点 O 恰好落在 上的点C 处,则图中阴影部分的面积为___________.
知识点三:求弓形的面积
6.如图,内接于⊙O,若∠A=⊙O的半径为 4,则阴影部分的面积为( )
A.4π-8 B.2π C.4π D.8π-8
7.[几何直观]如图,在 的正方形网格中有一半径为5 的圆,一条折线将它分成甲、乙两部分. S甲表示甲的面积,则
知识点四:求阴影部分的面积
8.如图,在 Rt△ABC中,. 以 BC 为直径作半圆,交AB 于点D,则阴影部分的面积是( )
A.π-1 D.2
9.如图, 中, AB 与⊙O 相切于点C,则图中阴影部分的面积为_____________.(结果保留π)
10.如图,在平行四边形中, 以点A 为圆心,AD 的长为半径画弧交AB 于点E,连接CE,则图中阴影部分的面积是____________.(结果保留π)
能力提升
11.[学科融合]如图,用一个半径为 10 cm的定滑轮带动重物上升,滑轮上一点 P 旋转了36°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
B.2πcm D.3πcm
12.如图,AB 是⊙O 的直径,直线DE 与⊙O 相切于点 C,过 A,B 分别作AD⊥DE,BE⊥DE,垂足为点 D,E,连接AC,BC,若 则 的长为( )
13.[空间观念]如图,在△ABC中, 点 D为AB 的中点,以点 D 为圆心作圆心角为 的扇形DEF,点C 恰在弧 EF 上,则图中阴影部分的面积为_____________.
14.[几何直观]如图,在单位长度为 1 米的平面直角坐标系中,曲线是由半径为 2 米、圆心角为 的 多次复制并首尾连接而成的.现有一点 P 从O(O 为坐标原点)出发,
以每秒 米的速度沿曲线向右运动,则在第2024秒时点 P 的坐标为___________.
培优创新
15.如图,AB 是⊙O 的直径,点C 是⊙O 上一点(与点 A,B 不重合),过点C 作直线PQ,使得
(1)求证:直线 PQ 是⊙O 的切线.
(2)过点 A 作 于点 D,交⊙O 于点E,若⊙O的半径为 2, 求图
中阴影部分的面积.
参考答案
1.18π 4. B 5.(1)A 6. A
8. D 11. B 12. D
[解析]过点A 作 垂足为C,则在 中, 米, (米), 米, 的长为 (米), (米),∴点 P 的坐标为
15.(1)证明:连接OC.∵AB 是⊙O的直径,∴即∴直线 PQ 是⊙O 的切线.
(2)解:连接OE. 又为等边三角形, ∴图中阴影部分的面积为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
