5.10 圆锥的侧面积同步练习(含答案)
文档属性
| 名称 | 5.10 圆锥的侧面积同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 11:43:42 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第五章 圆
10 圆锥的侧面积
基础闯关
知识点一:圆锥及其侧面展开图相关量的计算
命题角度1:求圆锥底面圆的半径
1.一个圆锥的侧面展开图是半径为6 的半圆,则这个圆锥的底面半径为( )
A.1.5 B.2 C.2.5 D.3
2.如图,在扇形OAB 中,半径OA与OB 的夹角为 点A 与点 B 的距离为,若扇形OAB 恰好是一个圆锥的侧面展开图,则该圆锥的底面半径为____________.
命题角度2:求圆锥的高
3.将弧长为 2πcm、圆心角为 的扇形围成一个圆锥的侧面,则这个圆锥的高是( )
4.如图,工人师傅准备从一块斜边AB长为 40 cm的等腰直角 材料上裁出一块以直角顶点O 为圆心的面积最大的扇形,然后用这块扇形材料做成无底的圆锥(接缝处忽略),则圆锥的高为__________cm.
命题角度3:求侧面展开图圆心角的度数
如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是 4:5,那么所需扇形铁皮的圆心角应为( )
知识点二:圆锥的侧面积和全面积的计算
命题角度1:求圆锥的侧面积
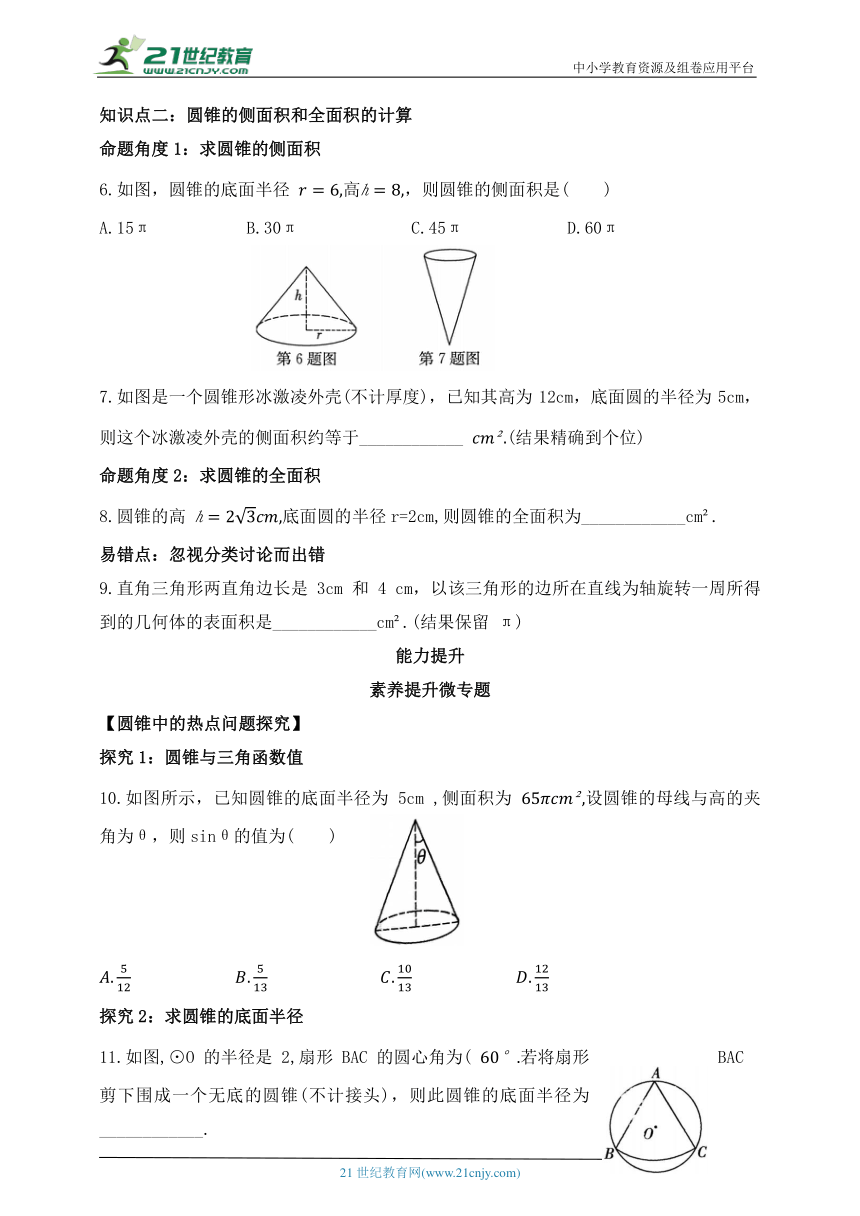
6.如图,圆锥的底面半径 高,则圆锥的侧面积是( )
A.15π B.30π C.45π D.60π
7.如图是一个圆锥形冰激凌外壳(不计厚度),已知其高为12cm,底面圆的半径为5cm,则这个冰激凌外壳的侧面积约等于____________ (结果精确到个位)
命题角度2:求圆锥的全面积
8.圆锥的高 底面圆的半径r=2cm,则圆锥的全面积为____________cm .
易错点:忽视分类讨论而出错
9.直角三角形两直角边长是 3cm 和 4 cm,以该三角形的边所在直线为轴旋转一周所得到的几何体的表面积是____________cm .(结果保留 π)
能力提升
素养提升微专题
【圆锥中的热点问题探究】
探究1:圆锥与三角函数值
10.如图所示,已知圆锥的底面半径为 5cm ,侧面积为 设圆锥的母线与高的夹角为θ,则sinθ的值为( )
探究2:求圆锥的底面半径
11.如图,⊙O 的半径是 2,扇形BAC的圆心角为( 若将扇形 BAC 剪下围成一个无底的圆锥(不计接头),则此圆锥的底面半径为____________.
探究3:圆锥与最短路径
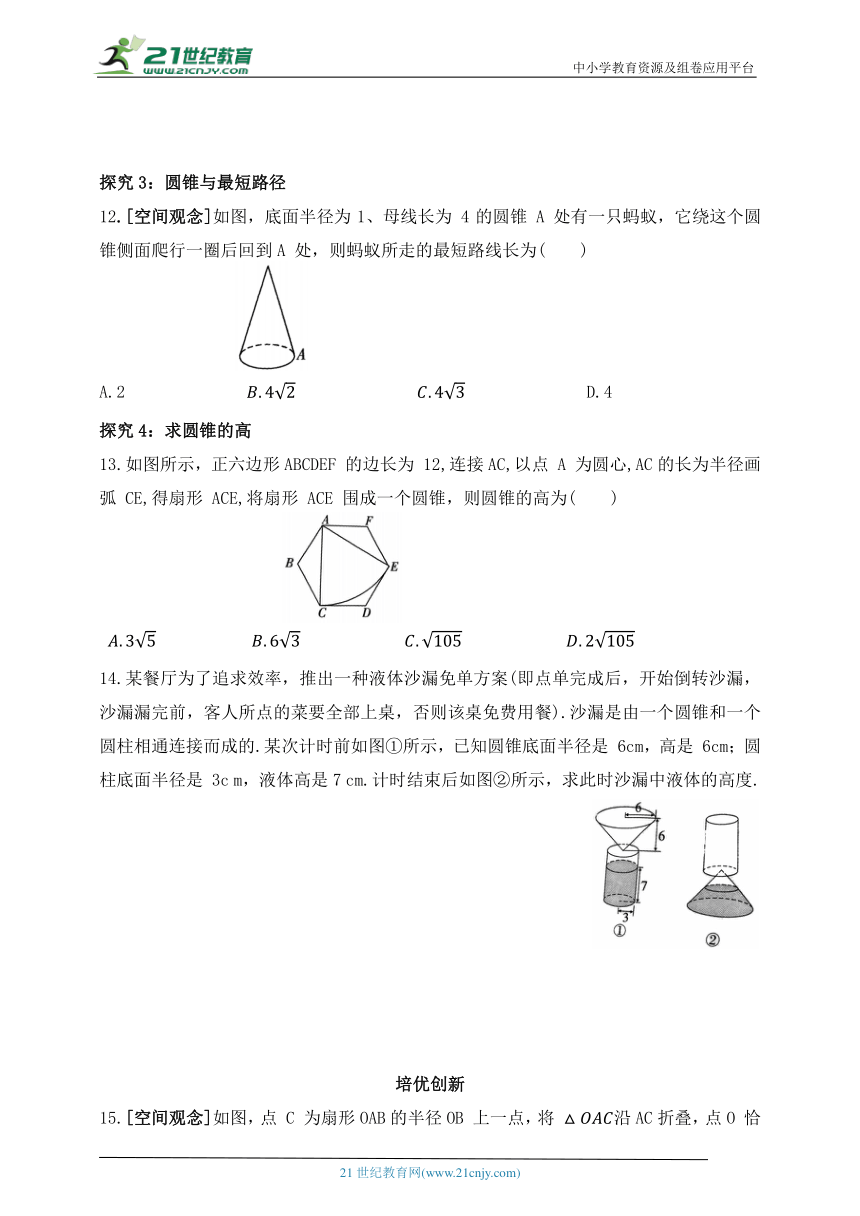
12.[空间观念]如图,底面半径为1、母线长为 4的圆锥 A 处有一只蚂蚁,它绕这个圆锥侧面爬行一圈后回到A 处,则蚂蚁所走的最短路线长为( )
A.2 D.4
探究4:求圆锥的高
13.如图所示,正六边形ABCDEF 的边长为 12,连接AC,以点 A 为圆心,AC的长为半径画弧 CE,得扇形 ACE,将扇形 ACE 围成一个圆锥,则圆锥的高为( )
14.某餐厅为了追求效率,推出一种液体沙漏免单方案(即点单完成后,开始倒转沙漏,沙漏漏完前,客人所点的菜要全部上桌,否则该桌免费用餐).沙漏是由一个圆锥和一个圆柱相通连接而成的.某次计时前如图①所示,已知圆锥底面半径是 6cm,高是 6cm;圆柱底面半径是 3c m,液体高是7 cm.计时结束后如图②所示,求此时沙漏中液体的高度.
培优创新
15.[空间观念]如图,点 C 为扇形OAB的半径OB 上一点,将 沿AC折叠,点O 恰好落在 上的点 D 处,且表示 的长, 表示 的长),若将此扇形OAB 围成一个圆锥,求圆锥的底面半径与母线长的比.
参考答案
1. D 2.
3. B [解析]设圆锥的底面半径为rcm,则2πr=2π,解得r=1.设圆锥的母线长为 l cm,则 解得 l=3,所以圆锥的高 故选 B.
5. A 6 . D 7 .204 8 .12π
9.36π 或24π或 [解析]由题意得该直角三角形的斜边当以3cm的边所在直线为轴旋转一周时,其所得到的几何体的表面积 当以4 c m的边所在直线为轴旋转一周时,其所得到的几何体的表面积 ;当以5cm的边所在直线为轴旋转一周时,其所得到的几何体为共底面的两个圆锥,易得其底面圆的半径为 所以此几何体的表面积
10. B
[解析]连接OA,作OD⊥AB于点D.在Rt△OAD中, 则 ∴扇形的弧长是设底面圆的半径是 r,则 解得
12. B [解析]∵底面圆的半径为1,∴底面周长等于2π.设圆锥的侧面展开后的扇形圆心角为 则 解得∴展开图的圆心角为 90°,∴蚂蚁所走的最短路线长为 故选 B.
13. D [解析]如图,过点 B 作 于点 P,连接CE.∵正六边形的每个内角都是 ∵AC=AE=CE,∴△ACE是等边三角形, .弧CE 的圆心角为60°,∴弧长=圆锥的底面半径 圆锥的高
14.解:如图,∵圆锥底面半径是 6cm,高是6cm,∴△ABC是等腰直角三角形,∴△CDE 也是等腰直角三角形,即CD= DE.由已知得,液体的体积为 圆锥的体积为 ∴计时结束后,圆锥中没有液体的部分体积为72π-63π=设计时结束后,沙漏中液体的高度 AD为x cm,则 解得 x=3,∴计时结束后,沙漏中液体的高度为 3cm.
15.解:如图,连接OD 交AC 于点M.由折叠的知识,得OM设圆锥的底面半径为r,母线长为 2 :9.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
10 圆锥的侧面积
基础闯关
知识点一:圆锥及其侧面展开图相关量的计算
命题角度1:求圆锥底面圆的半径
1.一个圆锥的侧面展开图是半径为6 的半圆,则这个圆锥的底面半径为( )
A.1.5 B.2 C.2.5 D.3
2.如图,在扇形OAB 中,半径OA与OB 的夹角为 点A 与点 B 的距离为,若扇形OAB 恰好是一个圆锥的侧面展开图,则该圆锥的底面半径为____________.
命题角度2:求圆锥的高
3.将弧长为 2πcm、圆心角为 的扇形围成一个圆锥的侧面,则这个圆锥的高是( )
4.如图,工人师傅准备从一块斜边AB长为 40 cm的等腰直角 材料上裁出一块以直角顶点O 为圆心的面积最大的扇形,然后用这块扇形材料做成无底的圆锥(接缝处忽略),则圆锥的高为__________cm.
命题角度3:求侧面展开图圆心角的度数
如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是 4:5,那么所需扇形铁皮的圆心角应为( )
知识点二:圆锥的侧面积和全面积的计算
命题角度1:求圆锥的侧面积
6.如图,圆锥的底面半径 高,则圆锥的侧面积是( )
A.15π B.30π C.45π D.60π
7.如图是一个圆锥形冰激凌外壳(不计厚度),已知其高为12cm,底面圆的半径为5cm,则这个冰激凌外壳的侧面积约等于____________ (结果精确到个位)
命题角度2:求圆锥的全面积
8.圆锥的高 底面圆的半径r=2cm,则圆锥的全面积为____________cm .
易错点:忽视分类讨论而出错
9.直角三角形两直角边长是 3cm 和 4 cm,以该三角形的边所在直线为轴旋转一周所得到的几何体的表面积是____________cm .(结果保留 π)
能力提升
素养提升微专题
【圆锥中的热点问题探究】
探究1:圆锥与三角函数值
10.如图所示,已知圆锥的底面半径为 5cm ,侧面积为 设圆锥的母线与高的夹角为θ,则sinθ的值为( )
探究2:求圆锥的底面半径
11.如图,⊙O 的半径是 2,扇形BAC的圆心角为( 若将扇形 BAC 剪下围成一个无底的圆锥(不计接头),则此圆锥的底面半径为____________.
探究3:圆锥与最短路径
12.[空间观念]如图,底面半径为1、母线长为 4的圆锥 A 处有一只蚂蚁,它绕这个圆锥侧面爬行一圈后回到A 处,则蚂蚁所走的最短路线长为( )
A.2 D.4
探究4:求圆锥的高
13.如图所示,正六边形ABCDEF 的边长为 12,连接AC,以点 A 为圆心,AC的长为半径画弧 CE,得扇形 ACE,将扇形 ACE 围成一个圆锥,则圆锥的高为( )
14.某餐厅为了追求效率,推出一种液体沙漏免单方案(即点单完成后,开始倒转沙漏,沙漏漏完前,客人所点的菜要全部上桌,否则该桌免费用餐).沙漏是由一个圆锥和一个圆柱相通连接而成的.某次计时前如图①所示,已知圆锥底面半径是 6cm,高是 6cm;圆柱底面半径是 3c m,液体高是7 cm.计时结束后如图②所示,求此时沙漏中液体的高度.
培优创新
15.[空间观念]如图,点 C 为扇形OAB的半径OB 上一点,将 沿AC折叠,点O 恰好落在 上的点 D 处,且表示 的长, 表示 的长),若将此扇形OAB 围成一个圆锥,求圆锥的底面半径与母线长的比.
参考答案
1. D 2.
3. B [解析]设圆锥的底面半径为rcm,则2πr=2π,解得r=1.设圆锥的母线长为 l cm,则 解得 l=3,所以圆锥的高 故选 B.
5. A 6 . D 7 .204 8 .12π
9.36π 或24π或 [解析]由题意得该直角三角形的斜边当以3cm的边所在直线为轴旋转一周时,其所得到的几何体的表面积 当以4 c m的边所在直线为轴旋转一周时,其所得到的几何体的表面积 ;当以5cm的边所在直线为轴旋转一周时,其所得到的几何体为共底面的两个圆锥,易得其底面圆的半径为 所以此几何体的表面积
10. B
[解析]连接OA,作OD⊥AB于点D.在Rt△OAD中, 则 ∴扇形的弧长是设底面圆的半径是 r,则 解得
12. B [解析]∵底面圆的半径为1,∴底面周长等于2π.设圆锥的侧面展开后的扇形圆心角为 则 解得∴展开图的圆心角为 90°,∴蚂蚁所走的最短路线长为 故选 B.
13. D [解析]如图,过点 B 作 于点 P,连接CE.∵正六边形的每个内角都是 ∵AC=AE=CE,∴△ACE是等边三角形, .弧CE 的圆心角为60°,∴弧长=圆锥的底面半径 圆锥的高
14.解:如图,∵圆锥底面半径是 6cm,高是6cm,∴△ABC是等腰直角三角形,∴△CDE 也是等腰直角三角形,即CD= DE.由已知得,液体的体积为 圆锥的体积为 ∴计时结束后,圆锥中没有液体的部分体积为72π-63π=设计时结束后,沙漏中液体的高度 AD为x cm,则 解得 x=3,∴计时结束后,沙漏中液体的高度为 3cm.
15.解:如图,连接OD 交AC 于点M.由折叠的知识,得OM设圆锥的底面半径为r,母线长为 2 :9.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
