苏科版八年级数学下册 9.4.2菱形的性质与判定 专练(含答案)
文档属性
| 名称 | 苏科版八年级数学下册 9.4.2菱形的性质与判定 专练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 321.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 13:00:37 | ||
图片预览




文档简介
9.4.2菱形的性质与判定专练
一.解答题
1.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG,如图1所示.
(1)证明平行四边形ECFG是菱形;
(2)若∠ABC=120°,连结BG、CG、DG,如图2所示,
①求证:△DGC≌△BGE;
②求∠BDG的度数;
(3)若∠ABC=90°,AB=8,AD=14,M是EF的中点,如图3所示,求DM的长.
2.如图,在四边形ABCD中,对角线AC、BD交于点O,AB∥DC,AB=BC,BD平分∠ABC,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=2,BD=4,求OE的长.
3.已知:如图,在 ABCD中,G、H分别是AD、BC的中点,E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F.
(1)求证:四边形GEHF是平行四边形;
(2)当 ABCD满足 条件时,四边形GEHF是菱形;
(3)若BD=2AB,
①探究四边形GEHF的形状,并说明理由;
②当AB=2,∠ABD=120°时,直接写出四边形GEHF的面积.
4.已知:如图,在四边形ABCD中,AD∥BC,∠B=90°,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.
(1)求证:四边形AFCE是菱形;
(2)若AB=6,BC=8,求EF的长.
5.如图,在 ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.
(1)求证:四边形AECF是菱形.
(2)若AB=6,BC=10,F为BC中点,求四边形AECF的面积.
6.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=OC,连接 CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为6,∠ABC=60°,求AE的长.
7.如图,在菱形ABCD中,∠B=60°.
(1)如图①,若点E、F分别在边AB、AD上,且BE=AF.求证:△CEF是等边三角形;
(2)小明发现若点E、F分别在边AB、AD上,且∠CEF=60°时△CEF也是等边三角形,并通过画图验证了猜想;小丽通过探索,认为应该以CE=EF为突破口构造两个三角形全等;小倩受到小丽的启发,尝试在BC上截取BM=BE,连接ME,如图②,很快就证明了△CEF是等边三角形,请你根据小倩的方法,写出完整的证明过程.
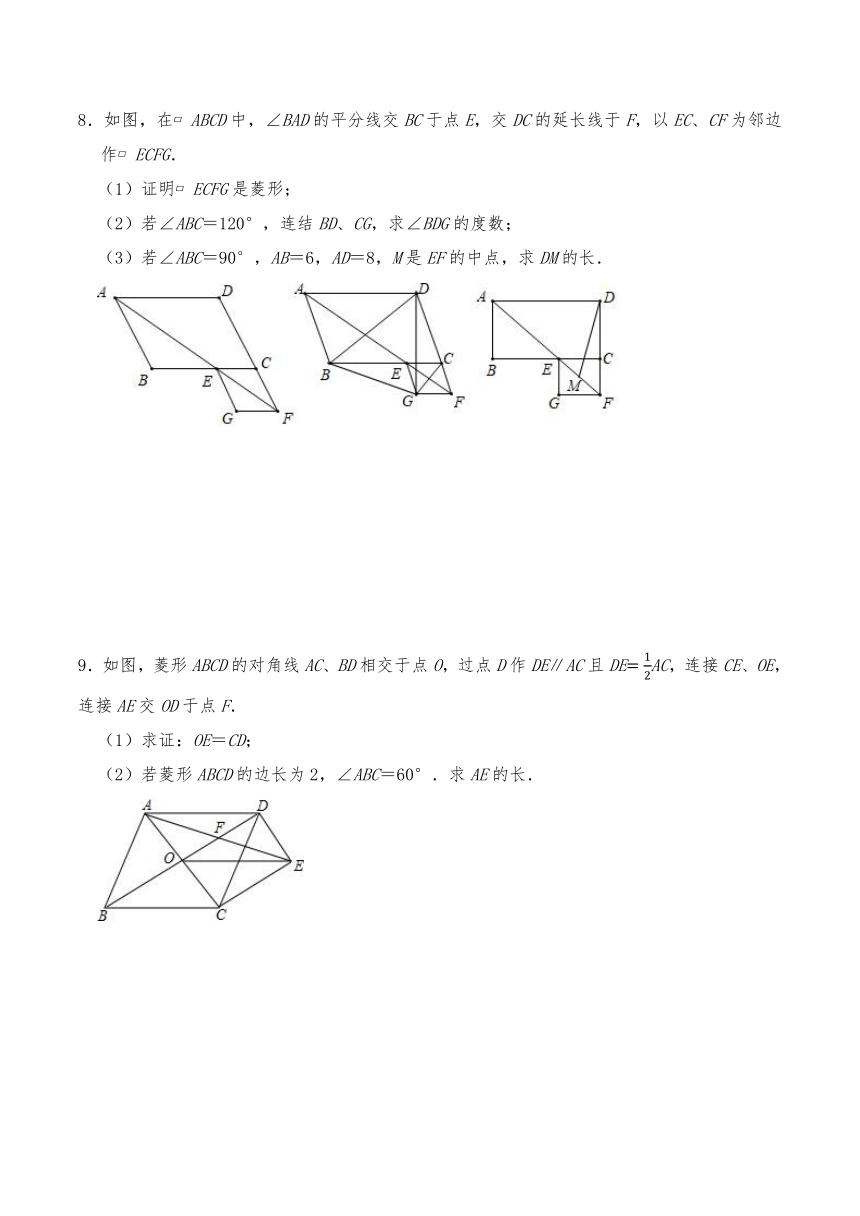
8.如图,在 ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作 ECFG.
(1)证明 ECFG是菱形;
(2)若∠ABC=120°,连结BD、CG,求∠BDG的度数;
(3)若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.
9.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DEAC,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°.求AE的长.
10.已知:如图,Rt△ABC中,∠B=90°,AB=8,BC=6,D是AB边上一个动点,连接CD,作CE∥AB,作AE∥CD交CE于点E,连接DE与AC交于点O.
(1)求证:OD=OE;
(2)若四边形ADCE是菱形,求菱形ADCE的面积.
11.如图,在菱形ABCD中,对角线AC和BD交于点O,E为AB上一动点,过点E作EF∥BD交AD于点F,连接BF、DE.
(1)若∠ABD=40°,求∠CAD的度数;
(2)求证:BF=DE.
12.如图,四边形ABCD是菱形,DE⊥AB交BA的延长线于点E,DF⊥BC交BC的延长线于点F.
(1)求证:DE=DF;
(2)若BE=8cm,DF=4cm,求菱形ABCD的面积.
13.如图,菱形ABCD中,E,F分别为AD,AB上的点,且AE=AF,连接EF并延长,交CB的延长线于点G,连接BD.
(1)求证:四边形EGBD是平行四边形;
(2)连接AG,若∠FGB=30°,GB=AE=3,求AG的长.
14.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD.过点C作CE⊥AB交AB的延长线于点E连接OE.
(1)求证;四边形ABCD是菱形;
(2)若AB,BD=4,求OE的长.
15.已知:如图,在菱形ABCD中,E,F分别是BC,CD上的点,
(1)如图1,若CE=CF;求证:AE=AF;
(2)如图2,若∠B=∠EAF=60°,∠BAE=20°,求∠CEF的度数.
16.如图,菱形ABCD的边长是10厘米,对角线AC,BD相交于点O,且AC=12厘米,点P,N分别在BD,AC上,点P从点D出发,以每秒2厘米的速度向终点B运动,点N从点C出发,以每秒1厘米的速度向点A运动,点P移动到点B后,点P,N停止运动.
(1)当运动多少秒时,△PON的面积是8平方厘米;
(2)如果△PON的面积为y,请你写出y关于时间t的函数表达式.
17.如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.
(1)证明不论E、F在BC、CD上如何滑动,总有BE=CF;
(2)当点E、F在BC、CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.
18.如图,在菱形ABCD中,∠A=60°,AB=4,E是AD边上的动点,作∠BEF=60°交CD于点F,在AB上取点G使AG=AE,连结EG.
(1)求∠EGB的度数;
(2)求证:EF=BE;
(3)若P是EF的中点,当AE为何值时,△EGP是等腰三角形.
19.如图,已知菱形ABCD的对角线AC,BD相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:四边形BECD是平行四边形;
(2)若∠E=60°,AB=6,求菱形ABCD的面积.
20.如图,在菱形ABCD中,点E、F分别在边AB、CD上,DF=BE,连接AF、CE.
(1)求证:∠AFD=∠CEB;
(2)点H、G分别是AF、CE上的点,若AH=CG,∠AEH+∠AFD=90°,试判断四边形HEGF是什么图形,并证明你的结论.
21.如图,在菱形ABCD中,∠A=60°,点E、F分别在边AB、BC上,△DEF是等边三角形.
(1)求证:BE=CF;
(2)若DG⊥AB,AD=6,AE=4,求EF的长.
22.如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC;
(2)若∠E=68°,求∠BAD的度数.
23.已知:在菱形ABCD中,点E是CD边上一点,过点E作EF⊥AC于点F,交BC边于点G,交AB延长线于点H.
(1)如图1,求证:BH=DE;
(2)如图2,当点E是CD边中点时,连接对角线BD交对角线AC于点O,连接OG、OE,在不添加任何辅助线和字母的情况下,请直接写出图2中所有的平行四边形(菱形除外).
24.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE:AC=1:2,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
25.已知:在菱形ABCD中,∠B=60°,点E和点F分别在BC边和CD边上,连接AE、AF、AC,∠EAF=60°.
(1)如图1,求证:BE=CF;
(2)如图2,当点E是BC边中点时,连接对角线BD分别交AE、AC、AF于点M、O、N,连接EF交对角线AC于点P,在不添加任何辅助线和字母的情况下,请直接写出图2中面积等于△PEC面积3倍的三角形或四边形.
26.菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图1,若E是BC的中点,∠AEF=60°,求证:F是CD的中点.
(2)如图2,若∠EAF=60°,∠BAE=20°,求∠FEC的度数.
27.已知,四边形ABCD是菱形,∠B=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.
(1)如图1,当点E是线段CB上任意一点时(点E不与B,C重合),求证:BE=CF;
(2)如图2,当点E在线段CB的延长线上,连接AC,在不添加任何辅助线的情况下,直接写出图2中三对相等的线段(菱形ABCD相等的边除外).
28.【猜想】如图1,在平行四边形ABCD中,点O是对角线AC的中点,过点O的直线分别交AD.BC于点E.F.若平行四边形ABCD的面积是8,则四边形CDEF的面积是 .
【探究】如图2,在菱形ABCD中,对角线相交于点O,过点O的直线分别交AD,BC于点E,F,若AC=5,BD=10,求四边形ABFE的面积.
【应用】如图3,在Rt△ABC中,∠BAC=90°,延长BC到点D,使DC=BC,连结AD,若AC=3,AD=2,则△ABD的面积是 .
答案
一.解答题
1.(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)①∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△DGC≌△BGE(SAS);
②∵△DGC≌△BGE,
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)方法一:如图3中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=8,AD=14,
∴BD=2,
∴DMBD.
方法二:过M作MH⊥DF于H,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形,
∴∠CEF=45°,
∴∠AEB=∠CEF=45°,
∴BE=AB=8,
∴CE=CF=14﹣8=6,
∵MH∥CE,EM=FM,
∴CH=FHCF=3,
∴MHCE=3,
∴DH=11,
∴DM.
2.(1)∵AB∥CD,
∴∠ABD=∠CDB,
∵BD平分∠ABC,
∴∠ABD=∠CBD
∴∠CDB=∠CBD,
∴BC=CD,且AB=BC
∴CD=AB,且AB∥CD
∴四边形ABCD是平行四边形,且AB=BC
∴四边形ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,BO=DO=2
∵AO4
∵CE⊥AB,AO=CO
∴EO=AO=CO=4
3.(1)证明:连接AC,如图1所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴BD的中点在AC上,
∵E、O、F分别是对角线BD上的四等分点,
∴E、F分别为OB、OD的中点,
∵G是AD的中点,
∴GF为△AOD的中位线,
∴GF∥OA,GFOA,
同理:EH∥OC,EHOC,
∴EH=GF,EH∥GF,
∴四边形GEHF是平行四边形;
(2)解:当 ABCD满足AB⊥BD条件时,四边形GEHF是菱形;理由如下:
连接GH,如图2所示:
则AG=BH,AG∥BH,
∴四边形ABHG是平行四边形,
∴AB∥GH,
∵AB⊥BD,
∴GH⊥BD,
∴GH⊥EF,
∴四边形GEHF是菱形;
故答案为:AB⊥BD;
(3)解:①四边形GEHF是矩形;理由如下:
由(2)得:四边形GEHF是平行四边形,
∴GH=AB,
∵BD=2AB,
∴ABBD=EF,
∴GH=EF,
∴四边形GEHF是矩形;
②作AM⊥BD于M,GN⊥BD于N,如图3所示:
则AM∥GN,
∵G是AD的中点,
∴GN是△ADM的中位线,
∴GNAM,
∵∠ABD=120°,
∴∠ABM=60°,
∴∠BAM=30°,
∴BMAB=1,AMBM,
∴GN,
∵BD=2AB=4,
∴EFBD=2,
∴△EFG的面积EF×GN2,
∴四边形GEHF的面积=2△EFG的面积.
4.证明:(1)∵EF是对角线AC的垂直平分线,
∴AO=CO,AC⊥EF,
∵AD∥BC,
∴∠AEO=∠CFO,
在△AEO和△CFO中,
,
∴△AEO≌△CFO(AAS),
∴AE=CF,
∴四边形AFCE是平行四边形,
又∵AC⊥EF,
∴四边形AFCE是菱形;
(2)∵∠B=90°,AB=6,BC=8,
∴AC,
∵四边形AFCE是菱形,
∴AF=FC,
在Rt△ABF中,设AF=FC=x,则BF=8﹣x
∴AB2+BF2=AF2,
∴62+(8﹣x)2=x2,
∴x,
∴OF,
∴EF=2OF.
5.证明:(1)如图,
∵四边形ABCD是平行四边形,AD=BC,且AD∥BC,DE=BF,
∴AE=CF,且AE∥CF,
∴四边形AECF为平行四边形,
∵AC⊥EF,
∴四边形AECF为菱形;
(2)∵四边形AECF是菱形,
∴AO=CO,
∵F为BC中点,
∴FO∥AB,FOAB=3,
∴∠BAC=∠FOC=90°,EF=6,
∵AB=6,BC=10,
∴AC=8,
∴S菱形AECF=24.
6.(1)证明:∵四边形ABCD是菱形,DEAC,
∴AC⊥BD,DE=OC.
∵DE∥AC,
∴四边形OCED是平行四边形,
∵AC⊥BD,四边形OCED是平行四边形,
∴四边形OCED是矩形,
∴OE=CD.
(2)解:∵菱形ABCD的边长为6,
∴AB=BC=CD=AD=6,BD⊥AC,AO=COAC.
∵∠ABC=60°,AB=BC,
∴△ABC是等边三角形,
∴AC=AB=6,
∵△AOD中BD⊥AC,AD=6,AO=3,
∴OD3,
∵四边形OCED是矩形,
∴CE=OD=3,
∵在Rt△ACE中,AC=6,CE=3,
∴AE3.
7.(1)证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵∠B=60°,
∴△ABC,△ADC都是等边三角形,
∴∠B=∠CAF=∠ACB=60°,
∵BC=AC,BE=AF,
∴△BEC≌△AFC(SAS),
∴CE=CF,∠BCE=∠ACF,
∴∠ECF=∠BCA=60°,
∴△ECF是等边三角形.
(2)证明:∵BE=BM,∠B=60°,
∴△BEM是等边三角形,
∴∠EMB=∠BEM=60°,∠EMC=∠AEM=120°,
∵AB=BC,∠EAF=120°,
∴AE=CM,∠EAF=∠EMC,
∵∠FEC=60°,
∴∠AEF+∠CEM=60°,
∵∠CEM+∠ECM=60°,
∴∠AEF=∠ECM,
∴△ECM≌△FEA(ASA),
∴EF=EC,∵∠FEC=60°,
∴△EFC是等边三角形.
8.解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△BEG≌△DCG(SAS),
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)如图2中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=6,AD=8,
∴BD=10,
∴DMBD=5.
9.(1)证明:在菱形ABCD中,OCAC.
∴DE=OC.
∵DE∥AC,
∴四边形OCED是平行四边形.
∵AC⊥BD,
∴平行四边形OCED是矩形.
∴OE=CD.
(2)在菱形ABCD中,∠ABC=60°,
∴AC=AB=2.
∴在矩形OCED中,
CE=OD.
在Rt△ACE中,
AE.
10.(1)证明:∵CE∥AB,AE∥CD,
∴四边形ADCE是平行四边形,
∴OD=OE;
(2)解:∵四边形ADCE是菱形,
∴AC⊥DE,AD=CD,
设AD=CD=x,则BD=8﹣x,
在Rt△BCD中,由勾股定理得:62+(8﹣x)2=x2,
解得:x,
∴AD,
∴菱形ADCE的面积=AD×BC6.
11.(1)解:∵四边形ABCD是菱形,
∴∠ABC=2∠ABD=80°,∠CAD∠BAD,AD∥BC,
∴∠BAD+∠ABC=180°,
∴∠BAD=180°﹣80°=100°,
∴∠CAD∠BAD=50°;
(2)证明:∵四边形ABCD是菱形,
∴AB=AD,
∴∠ABD=∠ADB,
∵EF∥BD,
∴∠AEF=∠ABD,∠AFE=∠ADB,
∴∠AEF=∠AFE,
∴AE=AF,
∴BE=DF,
在△BDF和△DBE中,
,
∴△BDF≌△DBE(SAS),
∴BF=DE.
12.(1)∵四边形ABCD是菱形,
∴BD是∠ABC的平分线,
又∵DE⊥AB,DF⊥BC,
∴DE=DF.
(2)设AB=AD=xcm,则AE=(8﹣x)cm,
∵∠E=90°,DE=DF=4,
∴Rt△ADE中,AE2+DE2=AD2,
即(8﹣x)2+42=x2,
解得x=5,
∴AB=5cm,
∴菱形ABCD的面积=AB×DE=5×4=20(cm2).
13.(1)证明:连接AC,如图1:
∵四边形ABCD是菱形,
∴AC平分∠DAB,且AC⊥BD,
∵AF=AE,
∴AC⊥EF,
∴EG∥BD.
又∵菱形ABCD中,ED∥BG,
∴四边形EGBD是平行四边形.
(2)解:过点A作AH⊥BC于H.
∵∠FGB=30°,
∴∠DBC=30°,
∴∠ABH=2∠DBC=60°,
∵GB=AE=3,
∴AB=AD=6,
在Rt△ABH中,∠AHB=90°,
∴AH=3,BH=3.
∴GH=6,
在Rt△AGH中,
根据勾股定理得,AG3.
14.(1)证明:∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴ ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=4,
∴OBBD=2,
在Rt△AOB中,AB,OB=2,
∴OA3,
∴AC=2OA=6,
∵CE⊥AB,
∴∠AEC=90°,
∴OEAC=3.
15.(1)证明:∵四边形ABCD为菱形,
∴∠B=∠D,AB=BC=CD=DA,
又∵CE=CF,
∴BE=DF,
在△ABE和△ADF中,,
∴△ABE≌△ADF(SAS),
∴AE=AF.
(2)解:连接AC,如图2所示:
∵四边形ABCD为菱形,
∴∠B=∠D=60°,AB=BC=CD=DA.
∴△ABC与△CDA为等边三角形,
∴AB=AC,∠B=∠ACD=∠BAC=60°,
∵∠EAF=60°,
∴∠BAE=∠CAF,
在△ABE和△ACF中,,
∴△ABE≌△ACF(ASA),
∴AE=AF,
∵∠EAF=60°,
∴△EAF为等边三角形,
∴∠AEF=60°,
∵∠AEC=∠B+∠BAE=∠AEF+∠CEF,
∴60°+20°=60°+∠CEF,
∴∠CEF=20°.
16.(1)∵菱形ABCD的边长是10厘米,AC=12厘米,
∴OC=6厘米,OD=8厘米,
设运动t秒时,△PON的面积是8平方厘米,根据题意,得
DP=2t,CN=t,
∴OP=8﹣2t,ON=6﹣t,
∴S△PONOP ON,
∴(8﹣2t)(6﹣t)=8,
解方程得,t1=2,t2=8,均符合题意,
答:当运动2秒或8秒时,△PON的面积是8平方厘米;
(2)根据题意,得
①当0<t≤4时,y(8﹣2t)(6﹣t);
②当4<t<6时,y(2t﹣8)(6﹣t);
③当6<t≤8时,y(2t﹣8)(t﹣6).
17.(1)如图,连接AC,
∵四边形ABCD为菱形,∠BAD=120°,
∴∠BAC=60°,
∵△AEF是等边三角形,
∴∠EAF=60°,
∴∠1+∠EAC=60°,∠3+∠EAC=60°,
∴∠1=∠3,
∵∠BAD=120°,
∴∠ABC=60°,
∴△ABC和△ACD为等边三角形,
∴∠4=60°,AC=AB,
∴在△ABE和△ACF中,
,
∴△ABE≌△ACF(ASA).
∴BE=CF;
(2)四边形AECF的面积不变,△CEF的周长发生变化.理由如下:
由(1)得△ABE≌△ACF,
则S△ABE=S△ACF,
故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,是定值,
作AH⊥BC于H点,则BH=2,
S四边形AECF=S△ABC.
△CEF的周长=CE+CF+EF=CE+BE+EF=BC+EF=BC+AE
由“垂线段最短”可知:当正三角形AEF的边AE与BC垂直时,边AE最短.
故△AEF的周长会随着AE的变化而变化,且当AE最短时,△CEF的周长会最小=4.
18.(1)解:∵∠A=60°,AG=AE,
∴△AGE是等边三角形,
∴∠AGE=60°,
∴∠EGB=120°;
(2)证明:由(1)知,∠EGB=120°,
∵四边形ABCD为菱形,
∴AB∥CD,AB=AD,
∴∠A+∠D=180°,
∵∠A=60°,
∴∠D=120°,
∴∠DEF+∠DFE=60°,
∴∠D=∠EGB,
∵△AGE是等边三角形,
∴AE=AG,∠AEG=60°,
∴DE=GB,
∵∠BEF=60°,
∴∠DEF+∠GEB=60°,
∴∠DFE=∠GEB,
∴△DFE≌△GEB(ASA),
∴EF=BE;
(3)解:∵△DFE≌△GEB,
∴DF=GE,
当EG=EP时,过E作EM⊥AB 垂足为M,
设AE=x,
∵△AGE是等边三角形,
∴AMx,EMx,
∴BM=4x,
∵P为EF的中点,
∴EF=2EP,
由(2)知EF=BE,
∴EB=2EG=2AE=2x,
在Rt△EBM中,EM2+BM2=EB2,
即(x)2+(4x)2=(2x)2,
解得,(舍去),
即AE;
当EG=GP时,过G作GQ⊥EF,垂足为Q,过B作BH⊥CD垂足为H,连接BF,设AE=x,
∵△AGE是等边三角形,
∴EG=x,
∵EF=EB,∠BEF=60°,
∴△BEF为等边三角形,
∴∠EFB=∠BEF=60°,EF=BF,
∵△BEG≌△EFD,
∴∠BEG=∠EFD,DF=EG,
∴∠GEQ=∠BFH,CF=4﹣x,
∵∠EQG=∠FHB=90°,
∴△EGQ∽△FBH,
∴EG:BF=EQ:FH,
设△BEF的边长为a,
则BF=EF=a,
∵P为EF的中点,
∴EPa,
∵EG=GP=x,
∴EQEPa,
在Rt△BCH中,BC=AB=4,∠C=∠A=60°,
∴CH=2,
∴BH,
∴HF=2﹣(4﹣x)=x﹣2,
∵BF2=BH2+HF2,
∴a2=()2+(x﹣2)2,
∵EG:BF=EQ:FH,
∴,
即a2=4x2﹣8x,
∴
解得,(舍去),
即AE;
当EP=GP时,点P在EG的中垂线上,即P点AC上,
而运动期间P不可能位于线段AC上,
∴P在AC上不存在,
综上,AE或;
即当AE为或时,△EGP是等腰三角形.
19.(1)证明:∵四边形ABCD是菱形
∴AB=CD=BC,AB∥CD,
又∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD是平行四边形;
(2)解:∵四边形BECD是平行四边形,
∴BD∥CE,BE=CD,BD=CE,
∵四边形ABCD是菱形,
∴AC⊥BD,AB=CD=6,
∴CE⊥AC,BE=AB=BC=CD=6,
∴AE=AB+BE=12,
∵AC⊥CE,
∴∠ACE=90°,
∵∠E=60°,
∴△BCE是等边三角形,∠CAE=30°,
∴BD=CE=BC=6,ACCE=6,
∴菱形ABCD的面积AC BD66=18.
20.(1)证明:∵四边形ABCD是菱形,
∴∠D=∠B,AD=BC,
在△ADF和△CBE中
∴△ADF≌△CBE(SAS),
∴∠AFD=∠CEB;
(2)四边形HEGF是矩形,
证明:∵四边形ABCD是菱形,
∴DC∥AB,
∴∠DCE=∠CEB,
∵∠AFD=∠CEB,
∴∠AFD=∠DCE,
∴AF∥CE,
∵△ADF≌△CBE,
∴AF=CE,
∵AH=CG,
∴AF﹣AH=CE﹣CG,
即HF=GE,
∴四边形HEGF是平行四边形,
∵∠AEH+∠AFD=90°,∠AFD=∠CEB,
∴∠AEH+∠CEB=90°,
∴∠HEG=180°﹣(∠AEH+∠CEB)=90°,
∴四边形HEGF是矩形.
21.(1)证明:∵四边形ABCD是菱形,
∴AB=AD=BC=DC,∠C=∠A=60°,
∴△ABD和△BCD是等边三角形,
∴∠BDC=60°,DC=DB,
∵△DEF是等边三角形,
∴∠EDF=60°,DF=DE,
∴∠CDF=∠BDE,
∴△CDF≌△BDE(SAS),
∴BE=CF;
(2)∴△ABD是等边三角形,DG⊥AB,
∴AG=BGABAD=3,
∴DGAG=3,
∴EG=AE﹣AG=1,
在Rt△DGE中,根据勾股定理,得
DE2,
∴EF=DE=2.
22.(1)证明:∵四边形ABCD是菱形,
∴DC∥AB,DC=AB.
∵BE=AB,
∴DC∥BE,DC=BE.
∴四边形BDCE为平行四边形.
∴BD=EC.
(2)∵四边形BDCE为平行四边形,
∴BD∥CE.
∴∠DBA=∠E=68°.
∵菱形ABCD,
∴AC⊥BD,AC平分∠BAD,
∴∠BAO=90°﹣∠DBA=22°.
∴∠BAD=2∠BAO=44°.
23.(1)证明:∵四边形ABCD是菱形,
∴BC=CD,AB∥CD,AC平分∠BCD,
∴∠GCF=∠ECF,
∵EF⊥AC,
∴∠GFC=∠EFC=90°,
在△GFC和△EFC中,,
∴△GFC≌△EFC(ASA),
∴CG=CE,∠CGF=∠CEF,
∵AB∥CD,
∴∠H=∠CEF,
∵∠BGH=∠CGF,
∴∠H=∠BGH,
∴BH=BG,
∵BC=CD,CG=CE,
∴BC﹣CG=CD﹣CE,
即BG=DE;
(2)解:所有的平行四边形(菱形除外)为平行四边形BHED、平行四边形BHGO、平行四边形OGED、平行四边形OBGE;理由如下:
∵四边形ABCD是菱形,
∴AB∥CD,
由(1)得:CG=CE,BH=BG=DE,
∴四边形BHED为平行四边形,
∵点E是CD边中点,BC=CD,
∴CE=DE=BG=CG,
∵四边形ABCD是菱形,
∴AB∥CD,OB=OD,
∴OE、O都G是△BCD的中位线,
∴OE∥BG,OG∥CD∥AB,OGCD=DE=BH,
∴四边形OBGE、四边形BHGO、四边形OGED都是平行四边形.
24.(1)证明:在菱形ABCD中,OCAC.
∵DE:AC=1:2,
∴DE=OC,
∵DE∥AC,
∴四边形OCED是平行四边形.
∵AC⊥BD,
∴平行四边形OCED是矩形.
∴OE=CD.
(2)解:在菱形ABCD中,∠ABC=60°,
∴AC=AB=2.
∴在矩形OCED中,
CE=OD.
在Rt△ACE中,
AE.
25.(1)证明:∵四边形ABCD是菱形,
∴AB=BC=CD,AC⊥BD,AB∥CD,AC平分∠BCD,
∴∠BCD+∠B=180°,
∵∠B=60°,
∴∠ACD=120°﹣60°=60°=∠B,△ABC是等边三角形,
∴AB=AC,∠BAC=∠BCA=60°,
∵∠BAC=∠BAE+∠EAC=60°,∠EAF=∠CAF+∠EAC=60°,
∴∠BAE=∠CAF,
在△ABE和△ACF中,,
∴△ABE≌△ACF(ASA),
∴BE=CF;
(2)解:图2中面积等于△PEC面积3倍的三角形为△AEP和△AFP,四边形为四边形BOPE和四边形△DOPF;理由如下:
由(1)得:△ABE≌△ACF,
∴BE=CF,AE=AF,
∵∠EAF=60°,
∴△AEF是等边三角形,
∵点E是BC边中点,
∴AE⊥BC,CE=BEBCCD=CF,
∴F是CD的中点,
∴EF是△BCD的中位线,
∴EF∥BD,
∴EP是△BOC的中位线,
∴PEOB,
∵AC⊥BD,∠BCD=120°,
∴EF⊥AC,∠CEF=∠CFE=30°,
∴PCCE,
设PC=x,则CE=2x,PEx,AECE=2x,
∵△PEC的面积PC×PExxx2,△AEC的面积CE×AE2x×2x=2x2,
∴△AEC的面积=4△PEC的面积,
∴△AEP的面积=3△PEC的面积,
同理:△AFP的面积=3△PEC的面积;
∵PE∥OB,PEOB,
∴△PEC∽△OBC,
∴△OBC的面积=4△PEC的面积,
∴四边形BOPE的面积=4△PEC的面积,
同理:四边形DOPF的面积=4△PEC的面积.
26.证明:(1)如图1所示:连接AC.
∵在菱形ABCD中,∠B=60°,
∴AB=BC=CD,∠C=180°﹣∠B=120°.
∴△ABC等边三角形.
∴E是BC的中点,
∴AE⊥BC.
∵∠AEF=60°,
∴∠FEC=90°﹣∠AEF=30°.
∴∠CFE=180°﹣∠FEC﹣∠ECF=180°﹣30°﹣120°=30°.
∴∠FEC=∠CFE.
∴EC=CF.
∵,
∴,
∴F是CD的中点;
(2)如图2所示:连接AC.
∵△ABC是等边三角形,
∴AB=AC,∠ACB=60°.
∴∠B=∠ACF=60°.
∵AD∥BC,
∴∠AEB=∠EAD=∠EAF+∠FAD=60°+∠FAD,∠AFC=∠D+∠FAD=60°+∠FAD.
∴∠AEB=∠AFC.
在△ABE和△ACF中,,
∴△ABE≌△ACF(AAS).
∴AE=AF.
∵∠EAF=60°,
∴△AEF是等边三角形.
∴∠AEF═60°,
∵∠AEF+∠FEC=∠B+∠BAE,
∴∠FEC=20°.
27.(1)证明:∵四边形ABCD是菱形,∠B=60°,
∴AB=BC=CD=AD,∠B=∠D=60°,
∴△ABC,△ADC是等边三角形,
∴∠BAC=∠DAC=60°,
∵∠BAC=∠EAF=60°,
∴∠BAE=∠CAF,
在△BAE和△CAF中,
,
∴△BAE≌△CAF(ASA),
∴BE=CF.
(2)解:AE=AF,BE=CF,CE=DF.
由(1)知△ABC,△ADC是等边三角形,
∴∠BAC=∠DAC=∠ACD=60°,
∵∠BAC=∠EAF=60°,∠ABE=∠ACF,
∴∠BAE=∠CAF,
∵AB=AC,
∴△BAE≌△CAF(ASA),
∴AE=AF,BE=CF,
∴BE+BC=CF+CD,
即CE=DF.
28.猜想:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC.
∴∠EAO=∠FCO,∠AEO=∠CFO,
在△AOE与△COF中,
,
∴△AEO≌△CFO(AAS),
∴四边形CDEF的面积=S△ACD ABCD的面积=4;
故答案为:4;
探究:∵四边形ABCD是菱形,
∴AD∥BC,AO=CO.
∴∠OAE=∠OCF,∠AEO=∠CFO,
∴在△AOE与△COF中,
,
∴△AOE≌△COF(AAS),
∵由菱形的对称性,得S△ABCS菱形ABCD,
∴S四边形ABFE=S△ABCAC BO5×10.
应用:延长AC到E使CE=AC=3,
在△ABC与△CDE中,
,
∴△ABC≌△CDE(SAS),
∴∠E=∠BAC=90°,
∴DE,
∴S△ABD=S△ADEAE DE6×2=6.
故答案为:6
一.解答题
1.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG,如图1所示.
(1)证明平行四边形ECFG是菱形;
(2)若∠ABC=120°,连结BG、CG、DG,如图2所示,
①求证:△DGC≌△BGE;
②求∠BDG的度数;
(3)若∠ABC=90°,AB=8,AD=14,M是EF的中点,如图3所示,求DM的长.
2.如图,在四边形ABCD中,对角线AC、BD交于点O,AB∥DC,AB=BC,BD平分∠ABC,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=2,BD=4,求OE的长.
3.已知:如图,在 ABCD中,G、H分别是AD、BC的中点,E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F.
(1)求证:四边形GEHF是平行四边形;
(2)当 ABCD满足 条件时,四边形GEHF是菱形;
(3)若BD=2AB,
①探究四边形GEHF的形状,并说明理由;
②当AB=2,∠ABD=120°时,直接写出四边形GEHF的面积.
4.已知:如图,在四边形ABCD中,AD∥BC,∠B=90°,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.
(1)求证:四边形AFCE是菱形;
(2)若AB=6,BC=8,求EF的长.
5.如图,在 ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.
(1)求证:四边形AECF是菱形.
(2)若AB=6,BC=10,F为BC中点,求四边形AECF的面积.
6.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=OC,连接 CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为6,∠ABC=60°,求AE的长.
7.如图,在菱形ABCD中,∠B=60°.
(1)如图①,若点E、F分别在边AB、AD上,且BE=AF.求证:△CEF是等边三角形;
(2)小明发现若点E、F分别在边AB、AD上,且∠CEF=60°时△CEF也是等边三角形,并通过画图验证了猜想;小丽通过探索,认为应该以CE=EF为突破口构造两个三角形全等;小倩受到小丽的启发,尝试在BC上截取BM=BE,连接ME,如图②,很快就证明了△CEF是等边三角形,请你根据小倩的方法,写出完整的证明过程.
8.如图,在 ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作 ECFG.
(1)证明 ECFG是菱形;
(2)若∠ABC=120°,连结BD、CG,求∠BDG的度数;
(3)若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.
9.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DEAC,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°.求AE的长.
10.已知:如图,Rt△ABC中,∠B=90°,AB=8,BC=6,D是AB边上一个动点,连接CD,作CE∥AB,作AE∥CD交CE于点E,连接DE与AC交于点O.
(1)求证:OD=OE;
(2)若四边形ADCE是菱形,求菱形ADCE的面积.
11.如图,在菱形ABCD中,对角线AC和BD交于点O,E为AB上一动点,过点E作EF∥BD交AD于点F,连接BF、DE.
(1)若∠ABD=40°,求∠CAD的度数;
(2)求证:BF=DE.
12.如图,四边形ABCD是菱形,DE⊥AB交BA的延长线于点E,DF⊥BC交BC的延长线于点F.
(1)求证:DE=DF;
(2)若BE=8cm,DF=4cm,求菱形ABCD的面积.
13.如图,菱形ABCD中,E,F分别为AD,AB上的点,且AE=AF,连接EF并延长,交CB的延长线于点G,连接BD.
(1)求证:四边形EGBD是平行四边形;
(2)连接AG,若∠FGB=30°,GB=AE=3,求AG的长.
14.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD.过点C作CE⊥AB交AB的延长线于点E连接OE.
(1)求证;四边形ABCD是菱形;
(2)若AB,BD=4,求OE的长.
15.已知:如图,在菱形ABCD中,E,F分别是BC,CD上的点,
(1)如图1,若CE=CF;求证:AE=AF;
(2)如图2,若∠B=∠EAF=60°,∠BAE=20°,求∠CEF的度数.
16.如图,菱形ABCD的边长是10厘米,对角线AC,BD相交于点O,且AC=12厘米,点P,N分别在BD,AC上,点P从点D出发,以每秒2厘米的速度向终点B运动,点N从点C出发,以每秒1厘米的速度向点A运动,点P移动到点B后,点P,N停止运动.
(1)当运动多少秒时,△PON的面积是8平方厘米;
(2)如果△PON的面积为y,请你写出y关于时间t的函数表达式.
17.如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.
(1)证明不论E、F在BC、CD上如何滑动,总有BE=CF;
(2)当点E、F在BC、CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.
18.如图,在菱形ABCD中,∠A=60°,AB=4,E是AD边上的动点,作∠BEF=60°交CD于点F,在AB上取点G使AG=AE,连结EG.
(1)求∠EGB的度数;
(2)求证:EF=BE;
(3)若P是EF的中点,当AE为何值时,△EGP是等腰三角形.
19.如图,已知菱形ABCD的对角线AC,BD相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:四边形BECD是平行四边形;
(2)若∠E=60°,AB=6,求菱形ABCD的面积.
20.如图,在菱形ABCD中,点E、F分别在边AB、CD上,DF=BE,连接AF、CE.
(1)求证:∠AFD=∠CEB;
(2)点H、G分别是AF、CE上的点,若AH=CG,∠AEH+∠AFD=90°,试判断四边形HEGF是什么图形,并证明你的结论.
21.如图,在菱形ABCD中,∠A=60°,点E、F分别在边AB、BC上,△DEF是等边三角形.
(1)求证:BE=CF;
(2)若DG⊥AB,AD=6,AE=4,求EF的长.
22.如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC;
(2)若∠E=68°,求∠BAD的度数.
23.已知:在菱形ABCD中,点E是CD边上一点,过点E作EF⊥AC于点F,交BC边于点G,交AB延长线于点H.
(1)如图1,求证:BH=DE;
(2)如图2,当点E是CD边中点时,连接对角线BD交对角线AC于点O,连接OG、OE,在不添加任何辅助线和字母的情况下,请直接写出图2中所有的平行四边形(菱形除外).
24.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE:AC=1:2,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
25.已知:在菱形ABCD中,∠B=60°,点E和点F分别在BC边和CD边上,连接AE、AF、AC,∠EAF=60°.
(1)如图1,求证:BE=CF;
(2)如图2,当点E是BC边中点时,连接对角线BD分别交AE、AC、AF于点M、O、N,连接EF交对角线AC于点P,在不添加任何辅助线和字母的情况下,请直接写出图2中面积等于△PEC面积3倍的三角形或四边形.
26.菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图1,若E是BC的中点,∠AEF=60°,求证:F是CD的中点.
(2)如图2,若∠EAF=60°,∠BAE=20°,求∠FEC的度数.
27.已知,四边形ABCD是菱形,∠B=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.
(1)如图1,当点E是线段CB上任意一点时(点E不与B,C重合),求证:BE=CF;
(2)如图2,当点E在线段CB的延长线上,连接AC,在不添加任何辅助线的情况下,直接写出图2中三对相等的线段(菱形ABCD相等的边除外).
28.【猜想】如图1,在平行四边形ABCD中,点O是对角线AC的中点,过点O的直线分别交AD.BC于点E.F.若平行四边形ABCD的面积是8,则四边形CDEF的面积是 .
【探究】如图2,在菱形ABCD中,对角线相交于点O,过点O的直线分别交AD,BC于点E,F,若AC=5,BD=10,求四边形ABFE的面积.
【应用】如图3,在Rt△ABC中,∠BAC=90°,延长BC到点D,使DC=BC,连结AD,若AC=3,AD=2,则△ABD的面积是 .
答案
一.解答题
1.(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)①∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△DGC≌△BGE(SAS);
②∵△DGC≌△BGE,
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)方法一:如图3中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=8,AD=14,
∴BD=2,
∴DMBD.
方法二:过M作MH⊥DF于H,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形,
∴∠CEF=45°,
∴∠AEB=∠CEF=45°,
∴BE=AB=8,
∴CE=CF=14﹣8=6,
∵MH∥CE,EM=FM,
∴CH=FHCF=3,
∴MHCE=3,
∴DH=11,
∴DM.
2.(1)∵AB∥CD,
∴∠ABD=∠CDB,
∵BD平分∠ABC,
∴∠ABD=∠CBD
∴∠CDB=∠CBD,
∴BC=CD,且AB=BC
∴CD=AB,且AB∥CD
∴四边形ABCD是平行四边形,且AB=BC
∴四边形ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,BO=DO=2
∵AO4
∵CE⊥AB,AO=CO
∴EO=AO=CO=4
3.(1)证明:连接AC,如图1所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴BD的中点在AC上,
∵E、O、F分别是对角线BD上的四等分点,
∴E、F分别为OB、OD的中点,
∵G是AD的中点,
∴GF为△AOD的中位线,
∴GF∥OA,GFOA,
同理:EH∥OC,EHOC,
∴EH=GF,EH∥GF,
∴四边形GEHF是平行四边形;
(2)解:当 ABCD满足AB⊥BD条件时,四边形GEHF是菱形;理由如下:
连接GH,如图2所示:
则AG=BH,AG∥BH,
∴四边形ABHG是平行四边形,
∴AB∥GH,
∵AB⊥BD,
∴GH⊥BD,
∴GH⊥EF,
∴四边形GEHF是菱形;
故答案为:AB⊥BD;
(3)解:①四边形GEHF是矩形;理由如下:
由(2)得:四边形GEHF是平行四边形,
∴GH=AB,
∵BD=2AB,
∴ABBD=EF,
∴GH=EF,
∴四边形GEHF是矩形;
②作AM⊥BD于M,GN⊥BD于N,如图3所示:
则AM∥GN,
∵G是AD的中点,
∴GN是△ADM的中位线,
∴GNAM,
∵∠ABD=120°,
∴∠ABM=60°,
∴∠BAM=30°,
∴BMAB=1,AMBM,
∴GN,
∵BD=2AB=4,
∴EFBD=2,
∴△EFG的面积EF×GN2,
∴四边形GEHF的面积=2△EFG的面积.
4.证明:(1)∵EF是对角线AC的垂直平分线,
∴AO=CO,AC⊥EF,
∵AD∥BC,
∴∠AEO=∠CFO,
在△AEO和△CFO中,
,
∴△AEO≌△CFO(AAS),
∴AE=CF,
∴四边形AFCE是平行四边形,
又∵AC⊥EF,
∴四边形AFCE是菱形;
(2)∵∠B=90°,AB=6,BC=8,
∴AC,
∵四边形AFCE是菱形,
∴AF=FC,
在Rt△ABF中,设AF=FC=x,则BF=8﹣x
∴AB2+BF2=AF2,
∴62+(8﹣x)2=x2,
∴x,
∴OF,
∴EF=2OF.
5.证明:(1)如图,
∵四边形ABCD是平行四边形,AD=BC,且AD∥BC,DE=BF,
∴AE=CF,且AE∥CF,
∴四边形AECF为平行四边形,
∵AC⊥EF,
∴四边形AECF为菱形;
(2)∵四边形AECF是菱形,
∴AO=CO,
∵F为BC中点,
∴FO∥AB,FOAB=3,
∴∠BAC=∠FOC=90°,EF=6,
∵AB=6,BC=10,
∴AC=8,
∴S菱形AECF=24.
6.(1)证明:∵四边形ABCD是菱形,DEAC,
∴AC⊥BD,DE=OC.
∵DE∥AC,
∴四边形OCED是平行四边形,
∵AC⊥BD,四边形OCED是平行四边形,
∴四边形OCED是矩形,
∴OE=CD.
(2)解:∵菱形ABCD的边长为6,
∴AB=BC=CD=AD=6,BD⊥AC,AO=COAC.
∵∠ABC=60°,AB=BC,
∴△ABC是等边三角形,
∴AC=AB=6,
∵△AOD中BD⊥AC,AD=6,AO=3,
∴OD3,
∵四边形OCED是矩形,
∴CE=OD=3,
∵在Rt△ACE中,AC=6,CE=3,
∴AE3.
7.(1)证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵∠B=60°,
∴△ABC,△ADC都是等边三角形,
∴∠B=∠CAF=∠ACB=60°,
∵BC=AC,BE=AF,
∴△BEC≌△AFC(SAS),
∴CE=CF,∠BCE=∠ACF,
∴∠ECF=∠BCA=60°,
∴△ECF是等边三角形.
(2)证明:∵BE=BM,∠B=60°,
∴△BEM是等边三角形,
∴∠EMB=∠BEM=60°,∠EMC=∠AEM=120°,
∵AB=BC,∠EAF=120°,
∴AE=CM,∠EAF=∠EMC,
∵∠FEC=60°,
∴∠AEF+∠CEM=60°,
∵∠CEM+∠ECM=60°,
∴∠AEF=∠ECM,
∴△ECM≌△FEA(ASA),
∴EF=EC,∵∠FEC=60°,
∴△EFC是等边三角形.
8.解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△BEG≌△DCG(SAS),
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)如图2中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=6,AD=8,
∴BD=10,
∴DMBD=5.
9.(1)证明:在菱形ABCD中,OCAC.
∴DE=OC.
∵DE∥AC,
∴四边形OCED是平行四边形.
∵AC⊥BD,
∴平行四边形OCED是矩形.
∴OE=CD.
(2)在菱形ABCD中,∠ABC=60°,
∴AC=AB=2.
∴在矩形OCED中,
CE=OD.
在Rt△ACE中,
AE.
10.(1)证明:∵CE∥AB,AE∥CD,
∴四边形ADCE是平行四边形,
∴OD=OE;
(2)解:∵四边形ADCE是菱形,
∴AC⊥DE,AD=CD,
设AD=CD=x,则BD=8﹣x,
在Rt△BCD中,由勾股定理得:62+(8﹣x)2=x2,
解得:x,
∴AD,
∴菱形ADCE的面积=AD×BC6.
11.(1)解:∵四边形ABCD是菱形,
∴∠ABC=2∠ABD=80°,∠CAD∠BAD,AD∥BC,
∴∠BAD+∠ABC=180°,
∴∠BAD=180°﹣80°=100°,
∴∠CAD∠BAD=50°;
(2)证明:∵四边形ABCD是菱形,
∴AB=AD,
∴∠ABD=∠ADB,
∵EF∥BD,
∴∠AEF=∠ABD,∠AFE=∠ADB,
∴∠AEF=∠AFE,
∴AE=AF,
∴BE=DF,
在△BDF和△DBE中,
,
∴△BDF≌△DBE(SAS),
∴BF=DE.
12.(1)∵四边形ABCD是菱形,
∴BD是∠ABC的平分线,
又∵DE⊥AB,DF⊥BC,
∴DE=DF.
(2)设AB=AD=xcm,则AE=(8﹣x)cm,
∵∠E=90°,DE=DF=4,
∴Rt△ADE中,AE2+DE2=AD2,
即(8﹣x)2+42=x2,
解得x=5,
∴AB=5cm,
∴菱形ABCD的面积=AB×DE=5×4=20(cm2).
13.(1)证明:连接AC,如图1:
∵四边形ABCD是菱形,
∴AC平分∠DAB,且AC⊥BD,
∵AF=AE,
∴AC⊥EF,
∴EG∥BD.
又∵菱形ABCD中,ED∥BG,
∴四边形EGBD是平行四边形.
(2)解:过点A作AH⊥BC于H.
∵∠FGB=30°,
∴∠DBC=30°,
∴∠ABH=2∠DBC=60°,
∵GB=AE=3,
∴AB=AD=6,
在Rt△ABH中,∠AHB=90°,
∴AH=3,BH=3.
∴GH=6,
在Rt△AGH中,
根据勾股定理得,AG3.
14.(1)证明:∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴ ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=4,
∴OBBD=2,
在Rt△AOB中,AB,OB=2,
∴OA3,
∴AC=2OA=6,
∵CE⊥AB,
∴∠AEC=90°,
∴OEAC=3.
15.(1)证明:∵四边形ABCD为菱形,
∴∠B=∠D,AB=BC=CD=DA,
又∵CE=CF,
∴BE=DF,
在△ABE和△ADF中,,
∴△ABE≌△ADF(SAS),
∴AE=AF.
(2)解:连接AC,如图2所示:
∵四边形ABCD为菱形,
∴∠B=∠D=60°,AB=BC=CD=DA.
∴△ABC与△CDA为等边三角形,
∴AB=AC,∠B=∠ACD=∠BAC=60°,
∵∠EAF=60°,
∴∠BAE=∠CAF,
在△ABE和△ACF中,,
∴△ABE≌△ACF(ASA),
∴AE=AF,
∵∠EAF=60°,
∴△EAF为等边三角形,
∴∠AEF=60°,
∵∠AEC=∠B+∠BAE=∠AEF+∠CEF,
∴60°+20°=60°+∠CEF,
∴∠CEF=20°.
16.(1)∵菱形ABCD的边长是10厘米,AC=12厘米,
∴OC=6厘米,OD=8厘米,
设运动t秒时,△PON的面积是8平方厘米,根据题意,得
DP=2t,CN=t,
∴OP=8﹣2t,ON=6﹣t,
∴S△PONOP ON,
∴(8﹣2t)(6﹣t)=8,
解方程得,t1=2,t2=8,均符合题意,
答:当运动2秒或8秒时,△PON的面积是8平方厘米;
(2)根据题意,得
①当0<t≤4时,y(8﹣2t)(6﹣t);
②当4<t<6时,y(2t﹣8)(6﹣t);
③当6<t≤8时,y(2t﹣8)(t﹣6).
17.(1)如图,连接AC,
∵四边形ABCD为菱形,∠BAD=120°,
∴∠BAC=60°,
∵△AEF是等边三角形,
∴∠EAF=60°,
∴∠1+∠EAC=60°,∠3+∠EAC=60°,
∴∠1=∠3,
∵∠BAD=120°,
∴∠ABC=60°,
∴△ABC和△ACD为等边三角形,
∴∠4=60°,AC=AB,
∴在△ABE和△ACF中,
,
∴△ABE≌△ACF(ASA).
∴BE=CF;
(2)四边形AECF的面积不变,△CEF的周长发生变化.理由如下:
由(1)得△ABE≌△ACF,
则S△ABE=S△ACF,
故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,是定值,
作AH⊥BC于H点,则BH=2,
S四边形AECF=S△ABC.
△CEF的周长=CE+CF+EF=CE+BE+EF=BC+EF=BC+AE
由“垂线段最短”可知:当正三角形AEF的边AE与BC垂直时,边AE最短.
故△AEF的周长会随着AE的变化而变化,且当AE最短时,△CEF的周长会最小=4.
18.(1)解:∵∠A=60°,AG=AE,
∴△AGE是等边三角形,
∴∠AGE=60°,
∴∠EGB=120°;
(2)证明:由(1)知,∠EGB=120°,
∵四边形ABCD为菱形,
∴AB∥CD,AB=AD,
∴∠A+∠D=180°,
∵∠A=60°,
∴∠D=120°,
∴∠DEF+∠DFE=60°,
∴∠D=∠EGB,
∵△AGE是等边三角形,
∴AE=AG,∠AEG=60°,
∴DE=GB,
∵∠BEF=60°,
∴∠DEF+∠GEB=60°,
∴∠DFE=∠GEB,
∴△DFE≌△GEB(ASA),
∴EF=BE;
(3)解:∵△DFE≌△GEB,
∴DF=GE,
当EG=EP时,过E作EM⊥AB 垂足为M,
设AE=x,
∵△AGE是等边三角形,
∴AMx,EMx,
∴BM=4x,
∵P为EF的中点,
∴EF=2EP,
由(2)知EF=BE,
∴EB=2EG=2AE=2x,
在Rt△EBM中,EM2+BM2=EB2,
即(x)2+(4x)2=(2x)2,
解得,(舍去),
即AE;
当EG=GP时,过G作GQ⊥EF,垂足为Q,过B作BH⊥CD垂足为H,连接BF,设AE=x,
∵△AGE是等边三角形,
∴EG=x,
∵EF=EB,∠BEF=60°,
∴△BEF为等边三角形,
∴∠EFB=∠BEF=60°,EF=BF,
∵△BEG≌△EFD,
∴∠BEG=∠EFD,DF=EG,
∴∠GEQ=∠BFH,CF=4﹣x,
∵∠EQG=∠FHB=90°,
∴△EGQ∽△FBH,
∴EG:BF=EQ:FH,
设△BEF的边长为a,
则BF=EF=a,
∵P为EF的中点,
∴EPa,
∵EG=GP=x,
∴EQEPa,
在Rt△BCH中,BC=AB=4,∠C=∠A=60°,
∴CH=2,
∴BH,
∴HF=2﹣(4﹣x)=x﹣2,
∵BF2=BH2+HF2,
∴a2=()2+(x﹣2)2,
∵EG:BF=EQ:FH,
∴,
即a2=4x2﹣8x,
∴
解得,(舍去),
即AE;
当EP=GP时,点P在EG的中垂线上,即P点AC上,
而运动期间P不可能位于线段AC上,
∴P在AC上不存在,
综上,AE或;
即当AE为或时,△EGP是等腰三角形.
19.(1)证明:∵四边形ABCD是菱形
∴AB=CD=BC,AB∥CD,
又∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD是平行四边形;
(2)解:∵四边形BECD是平行四边形,
∴BD∥CE,BE=CD,BD=CE,
∵四边形ABCD是菱形,
∴AC⊥BD,AB=CD=6,
∴CE⊥AC,BE=AB=BC=CD=6,
∴AE=AB+BE=12,
∵AC⊥CE,
∴∠ACE=90°,
∵∠E=60°,
∴△BCE是等边三角形,∠CAE=30°,
∴BD=CE=BC=6,ACCE=6,
∴菱形ABCD的面积AC BD66=18.
20.(1)证明:∵四边形ABCD是菱形,
∴∠D=∠B,AD=BC,
在△ADF和△CBE中
∴△ADF≌△CBE(SAS),
∴∠AFD=∠CEB;
(2)四边形HEGF是矩形,
证明:∵四边形ABCD是菱形,
∴DC∥AB,
∴∠DCE=∠CEB,
∵∠AFD=∠CEB,
∴∠AFD=∠DCE,
∴AF∥CE,
∵△ADF≌△CBE,
∴AF=CE,
∵AH=CG,
∴AF﹣AH=CE﹣CG,
即HF=GE,
∴四边形HEGF是平行四边形,
∵∠AEH+∠AFD=90°,∠AFD=∠CEB,
∴∠AEH+∠CEB=90°,
∴∠HEG=180°﹣(∠AEH+∠CEB)=90°,
∴四边形HEGF是矩形.
21.(1)证明:∵四边形ABCD是菱形,
∴AB=AD=BC=DC,∠C=∠A=60°,
∴△ABD和△BCD是等边三角形,
∴∠BDC=60°,DC=DB,
∵△DEF是等边三角形,
∴∠EDF=60°,DF=DE,
∴∠CDF=∠BDE,
∴△CDF≌△BDE(SAS),
∴BE=CF;
(2)∴△ABD是等边三角形,DG⊥AB,
∴AG=BGABAD=3,
∴DGAG=3,
∴EG=AE﹣AG=1,
在Rt△DGE中,根据勾股定理,得
DE2,
∴EF=DE=2.
22.(1)证明:∵四边形ABCD是菱形,
∴DC∥AB,DC=AB.
∵BE=AB,
∴DC∥BE,DC=BE.
∴四边形BDCE为平行四边形.
∴BD=EC.
(2)∵四边形BDCE为平行四边形,
∴BD∥CE.
∴∠DBA=∠E=68°.
∵菱形ABCD,
∴AC⊥BD,AC平分∠BAD,
∴∠BAO=90°﹣∠DBA=22°.
∴∠BAD=2∠BAO=44°.
23.(1)证明:∵四边形ABCD是菱形,
∴BC=CD,AB∥CD,AC平分∠BCD,
∴∠GCF=∠ECF,
∵EF⊥AC,
∴∠GFC=∠EFC=90°,
在△GFC和△EFC中,,
∴△GFC≌△EFC(ASA),
∴CG=CE,∠CGF=∠CEF,
∵AB∥CD,
∴∠H=∠CEF,
∵∠BGH=∠CGF,
∴∠H=∠BGH,
∴BH=BG,
∵BC=CD,CG=CE,
∴BC﹣CG=CD﹣CE,
即BG=DE;
(2)解:所有的平行四边形(菱形除外)为平行四边形BHED、平行四边形BHGO、平行四边形OGED、平行四边形OBGE;理由如下:
∵四边形ABCD是菱形,
∴AB∥CD,
由(1)得:CG=CE,BH=BG=DE,
∴四边形BHED为平行四边形,
∵点E是CD边中点,BC=CD,
∴CE=DE=BG=CG,
∵四边形ABCD是菱形,
∴AB∥CD,OB=OD,
∴OE、O都G是△BCD的中位线,
∴OE∥BG,OG∥CD∥AB,OGCD=DE=BH,
∴四边形OBGE、四边形BHGO、四边形OGED都是平行四边形.
24.(1)证明:在菱形ABCD中,OCAC.
∵DE:AC=1:2,
∴DE=OC,
∵DE∥AC,
∴四边形OCED是平行四边形.
∵AC⊥BD,
∴平行四边形OCED是矩形.
∴OE=CD.
(2)解:在菱形ABCD中,∠ABC=60°,
∴AC=AB=2.
∴在矩形OCED中,
CE=OD.
在Rt△ACE中,
AE.
25.(1)证明:∵四边形ABCD是菱形,
∴AB=BC=CD,AC⊥BD,AB∥CD,AC平分∠BCD,
∴∠BCD+∠B=180°,
∵∠B=60°,
∴∠ACD=120°﹣60°=60°=∠B,△ABC是等边三角形,
∴AB=AC,∠BAC=∠BCA=60°,
∵∠BAC=∠BAE+∠EAC=60°,∠EAF=∠CAF+∠EAC=60°,
∴∠BAE=∠CAF,
在△ABE和△ACF中,,
∴△ABE≌△ACF(ASA),
∴BE=CF;
(2)解:图2中面积等于△PEC面积3倍的三角形为△AEP和△AFP,四边形为四边形BOPE和四边形△DOPF;理由如下:
由(1)得:△ABE≌△ACF,
∴BE=CF,AE=AF,
∵∠EAF=60°,
∴△AEF是等边三角形,
∵点E是BC边中点,
∴AE⊥BC,CE=BEBCCD=CF,
∴F是CD的中点,
∴EF是△BCD的中位线,
∴EF∥BD,
∴EP是△BOC的中位线,
∴PEOB,
∵AC⊥BD,∠BCD=120°,
∴EF⊥AC,∠CEF=∠CFE=30°,
∴PCCE,
设PC=x,则CE=2x,PEx,AECE=2x,
∵△PEC的面积PC×PExxx2,△AEC的面积CE×AE2x×2x=2x2,
∴△AEC的面积=4△PEC的面积,
∴△AEP的面积=3△PEC的面积,
同理:△AFP的面积=3△PEC的面积;
∵PE∥OB,PEOB,
∴△PEC∽△OBC,
∴△OBC的面积=4△PEC的面积,
∴四边形BOPE的面积=4△PEC的面积,
同理:四边形DOPF的面积=4△PEC的面积.
26.证明:(1)如图1所示:连接AC.
∵在菱形ABCD中,∠B=60°,
∴AB=BC=CD,∠C=180°﹣∠B=120°.
∴△ABC等边三角形.
∴E是BC的中点,
∴AE⊥BC.
∵∠AEF=60°,
∴∠FEC=90°﹣∠AEF=30°.
∴∠CFE=180°﹣∠FEC﹣∠ECF=180°﹣30°﹣120°=30°.
∴∠FEC=∠CFE.
∴EC=CF.
∵,
∴,
∴F是CD的中点;
(2)如图2所示:连接AC.
∵△ABC是等边三角形,
∴AB=AC,∠ACB=60°.
∴∠B=∠ACF=60°.
∵AD∥BC,
∴∠AEB=∠EAD=∠EAF+∠FAD=60°+∠FAD,∠AFC=∠D+∠FAD=60°+∠FAD.
∴∠AEB=∠AFC.
在△ABE和△ACF中,,
∴△ABE≌△ACF(AAS).
∴AE=AF.
∵∠EAF=60°,
∴△AEF是等边三角形.
∴∠AEF═60°,
∵∠AEF+∠FEC=∠B+∠BAE,
∴∠FEC=20°.
27.(1)证明:∵四边形ABCD是菱形,∠B=60°,
∴AB=BC=CD=AD,∠B=∠D=60°,
∴△ABC,△ADC是等边三角形,
∴∠BAC=∠DAC=60°,
∵∠BAC=∠EAF=60°,
∴∠BAE=∠CAF,
在△BAE和△CAF中,
,
∴△BAE≌△CAF(ASA),
∴BE=CF.
(2)解:AE=AF,BE=CF,CE=DF.
由(1)知△ABC,△ADC是等边三角形,
∴∠BAC=∠DAC=∠ACD=60°,
∵∠BAC=∠EAF=60°,∠ABE=∠ACF,
∴∠BAE=∠CAF,
∵AB=AC,
∴△BAE≌△CAF(ASA),
∴AE=AF,BE=CF,
∴BE+BC=CF+CD,
即CE=DF.
28.猜想:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC.
∴∠EAO=∠FCO,∠AEO=∠CFO,
在△AOE与△COF中,
,
∴△AEO≌△CFO(AAS),
∴四边形CDEF的面积=S△ACD ABCD的面积=4;
故答案为:4;
探究:∵四边形ABCD是菱形,
∴AD∥BC,AO=CO.
∴∠OAE=∠OCF,∠AEO=∠CFO,
∴在△AOE与△COF中,
,
∴△AOE≌△COF(AAS),
∵由菱形的对称性,得S△ABCS菱形ABCD,
∴S四边形ABFE=S△ABCAC BO5×10.
应用:延长AC到E使CE=AC=3,
在△ABC与△CDE中,
,
∴△ABC≌△CDE(SAS),
∴∠E=∠BAC=90°,
∴DE,
∴S△ABD=S△ADEAE DE6×2=6.
故答案为:6
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
