人教版(2019)必修一 第三章 拓展力的合成与分解 课件 (共37张PPT)
文档属性
| 名称 | 人教版(2019)必修一 第三章 拓展力的合成与分解 课件 (共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-02 20:48:18 | ||
图片预览




文档简介
(共39张PPT)
盛大私服
3.4拓展
力的合成和分解
一、两个共点力的合力求解
NUMBER.
>>01
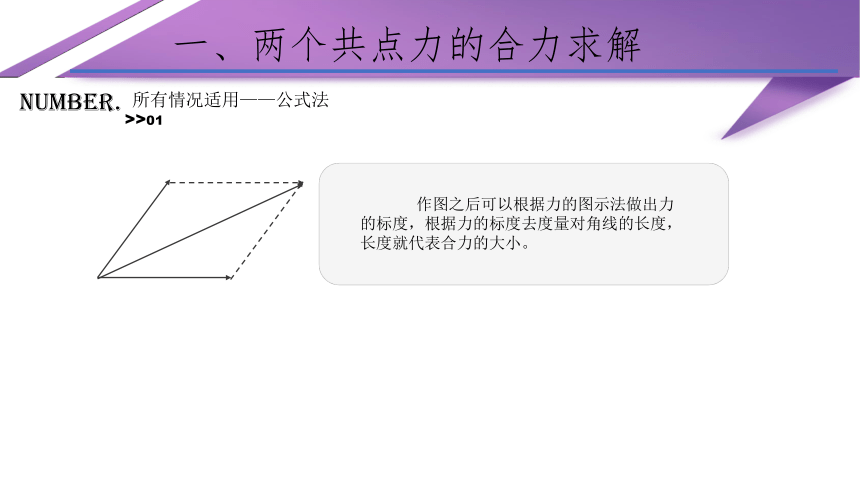
所有情况适用——公式法
作图之后可以根据力的图示法做出力的标度,根据力的标度去度量对角线的长度,长度就代表合力的大小。
一、两个共点力的合力求解
NUMBER.
>>01
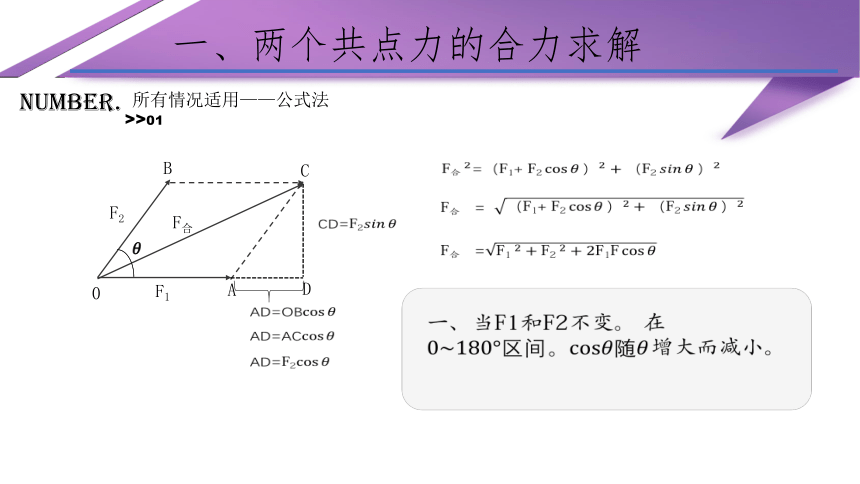
所有情况适用——公式法
一、当F1和F2不变。 在增大而减小。
0
A
C
B
D
AD=OB
AD=AC
F2
F1
F合
AD=F2
CD=F2
=
=
=
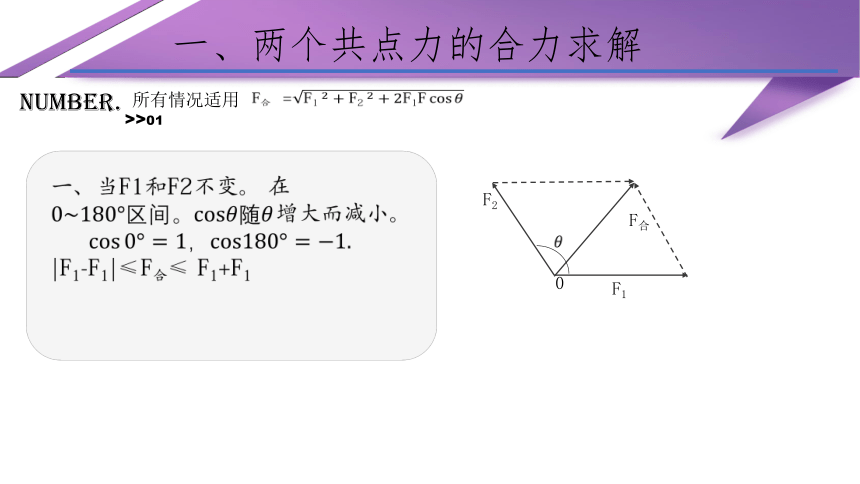
一、当F1和F2不变。 在增大而减小。
|F1-F1|≤F合≤ F1+F1
一、两个共点力的合力求解
NUMBER.
>>01
所有情况适用
0
F2
F1
F合
=
一、两个共点力的合力求解
NUMBER.
>>02
垂直用勾股
0
F2
F1
F合
=
一、两个共点力的合力求解
NUMBER.
>>02
两力相等角度为
0
F2
F1
F合
F合=2F1cos
1.当=60°时, F合=
2.当=90°时, F合=
3.当=120°时, F合=
一、两个共点力的合力求解
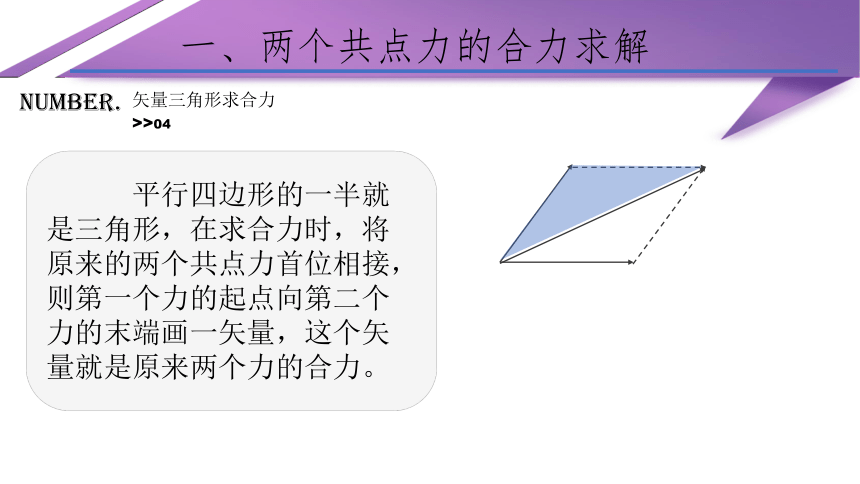
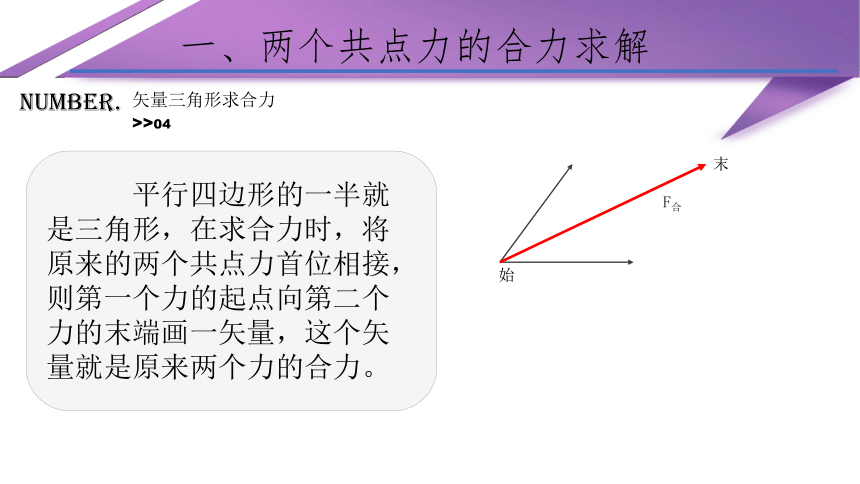
平行四边形的一半就是三角形,在求合力时,将原来的两个共点力首位相接,则第一个力的起点向第二个力的末端画一矢量,这个矢量就是原来两个力的合力。
矢量三角形求合力
>>04
平行四边形的一半就是三角形,在求合力时,将原来的两个共点力首位相接,则第一个力的起点向第二个力的末端画一矢量,这个矢量就是原来两个力的合力。
始
末
F合
一、两个共点力的合力求解
矢量三角形求合力
二、多个共点力的合力求解
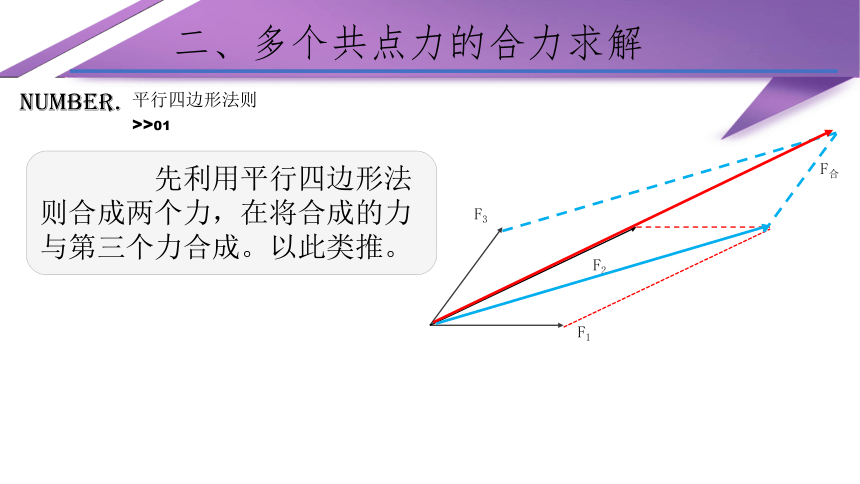
先利用平行四边形法则合成两个力,在将合成的力与第三个力合成。以此类推。
F合
F2
平行四边形法则
>>04
F1
F3
二、多个共点力的合力求解
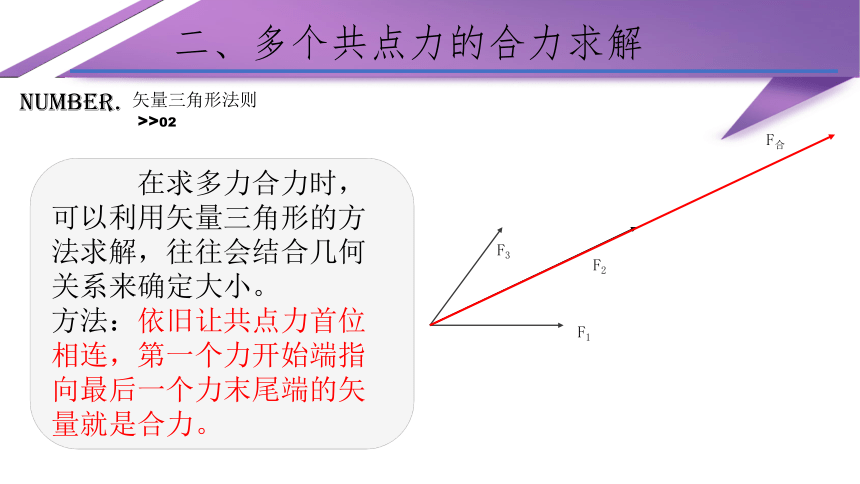
在求多力合力时,可以利用矢量三角形的方法求解,往往会结合几何关系来确定大小。
方法:依旧让共点力首位相连,第一个力开始端指向最后一个力末尾端的矢量就是合力。
F合
F2
矢量三角形法则
>>04
F1
F3
二、多个共点力的合力求解
F合
F2
>>04
F1
F3
F合
F2
F1
F3
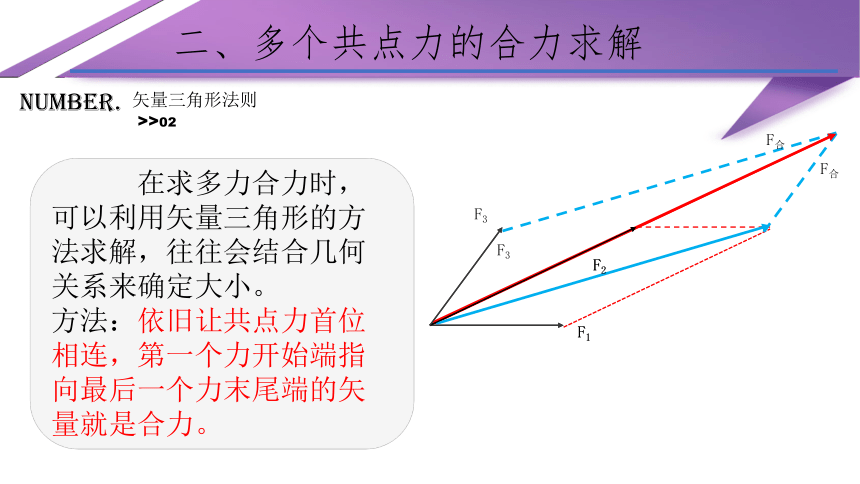
在求多力合力时,可以利用矢量三角形的方法求解,往往会结合几何关系来确定大小。
方法:依旧让共点力首位相连,第一个力开始端指向最后一个力末尾端的矢量就是合力。
矢量三角形法则
在求多力合力时,可以利用矢量三角形的方法求解,往往会结合几何关系来确定大小。
方法:依旧让共点力首位相连,第一个力开始端指向最后一个力末尾端的矢量就是合力。
二、多个共点力的合力求解
>>04
矢量三角形法则
O
F1
F2
F3
F4
F5
在求多力合力时,可以利用矢量三角形的方法求解,往往会结合几何关系来确定大小。
方法:依旧让共点力首位相连,第一个力开始端指向最后一个力末尾端的矢量就是合力。
二、多个共点力的合力求解
>>04
矢量三角形法则
O
F1
F2
F3
F4
F5
在求多力合力时,可以利用矢量三角形的方法求解,往往会结合几何关系来确定大小。
方法:依旧让共点力首位相连,第一个力开始端指向最后一个力末尾端的矢量就是合力。
二、多个共点力的合力求解
>>04
矢量三角形法则
O
F合=3F3=30N
二、多个共点力的合力求解
>>04
F1
F3
在求多力合力时,可以利用矢量三角形的方法求解,往往会结合几何关系来确定大小。
方法:依旧让共点力首尾相连,第一个力开始端指向最后一个力末尾端的矢量就是合力。
矢量三角形法则
F2
F合
二、多个共点力的合力求解
>>04
F1
F3
在求多力合力时,可以利用矢量三角形的方法求解,往往会结合几何关系来确定大小。
方法:依旧让共点力首尾相连,第一个力开始端指向最后一个力末尾端的矢量就是合力。
矢量三角形法则
F2
F4
直接构成封闭图形,则合力为零。即共点力平衡。
F8
F8
F8= F1
F8= F1
F8= F1
F8
F8
F8
F8= F1
F8= F1
F8= F1
F8
2F1
2F1
F1
F1
F1
2F1
C
力的分解
力的分解是力的合成的逆过程,通常使用平行四边形法则、矢量三角形法则、正交分解等方法。
力的合成与分解是互为逆运算。
力的分解
>>04
平行四边形法则
F
F1
F2
三角形法则
>>02
F
F1
F2
力的分解
正交分解——最重要的方法
方法:
1.以共点力的作用点为坐标原点,画直角坐标系。
2.坐标系的画线原则让尽量多的力落在坐标轴上。
3.正交分解不在坐标轴上的力,使得分解的力落在xy轴上。
4.对x.y轴的力进行合成。
5.求最终合力。
F1
F2
F3
F4
x
y
F5
F6
三角函数知识的补充
正交分解——最重要的方法
方法:
1.以共点力的作用点为坐标原点,画指标坐标系。
2.坐标系的画线原则让尽量多的力落在坐标轴上。
3.正交分解不在坐标轴上的力,使得分解的力落在xy轴上。
4.对x.y轴的力进行合成。
5.求最终合力。
某同学为了研究三角形承重结构各部分受力大小的规律,设计如图
所示的装置:一长度 的轻质细杆, 端通过光滑铰链连接
于竖直墙上, 端系上轻质细绳,细绳水平,另一端系于竖直墙上 点,
点悬挂一质量为 的重物,该系统保持静止状态。
系统保持静止状态。已知此时细绳长度为 ,重力加速度 取 。
x
y
F1
F1
x
y
F1
F1
(1)求此时轻绳 和轻杆 受到的弹力大小。
解析: 点受力如图甲所示,设 为 ,
水平方向 ,
竖直方向 ,
解得 , 。
F1
(2)若保持细杆 位置不动,只改变轻绳 的长度及
点位置,要使系统静止且绳子承受的拉力最小,求此时
轻绳 的长度及所受拉力大小。
解析:当 绳与 杆垂直时受到的拉力最小,如图乙所示,
此时细绳 长度为
解得
细绳拉力
解得 。
F
一定条件下力的分解
无条件限制,无数种分解方法
已知合力F和两个分力的方向
F
唯一解
F1
F2
F
,但两分力不能共线,共线就有无数种解。
已知合力F和两个分力的大小
F1
F2
F
利用三角形法则,分力F1和F2首尾相接
一定条件下力的分解
无条件限制,无数种分解方法
已知合力F和两个分力的方向
F
唯一解
,但两分力不能共线,共线就有无数种解。
已知合力F和两个分力的大小
F1
F2
F
利用三角形法则,分力F1和F2首尾相接
F1
F2
1.两圆相交,两个交点。
即|F1-F1|≤F合≤ F1+F1
有两种分解方法
F1
F2
一定条件下力的分解
无条件限制,无数种分解方法
已知合力F和两个分力的方向
F
唯一解
,但两分力不能共线,共线就有无数种解。
已知合力F和两个分力的大小
F1
F2
F
利用三角形法则,分力F1和F2首尾相接
F1
F2
2.两圆相切,一个交点。
一定条件下力的分解
无条件限制,无数种分解方法
已知合力F和两个分力的方向
F
唯一解
,但两分力不能共线,共线就有无数种解。
已知合力F和两个分力的大小
F1
F2
F
利用三角形法则,分力F1和F2首尾相接
F1
F2
2.两圆相切,一个交点。
即|F1-F1|=F合或F合= F1+F1
有一种分解方法
一定条件下力的分解
无条件限制,无数种分解方法
已知合力F和两个分力的方向
F
唯一解
,但两分力不能共线,共线就有无数种解。
已知合力F和两个分力的大小
F1
F2
F
利用三角形法则,分力F1和F2首尾相接
F1
F2
2.两圆内含,无交点。
即|F1-F1|>F合无解
一定条件下力的分解
无条件限制,无数种分解方法
已知合力F和两个分力的方向
F
唯一解
,但两分力不能共线,共线就有无数种解。
已知合力F和两个分力的大小
F1
F2
F
利用三角形法则,分力F1和F2首尾相接
F1
F2
3.两圆相离,无交点。
即即|F1-F1|>F合
或F> F1+F1 无解
一定条件下力的分解
已知合力F和F1的大小以及F2的方向,若F与F2的夹角为
>>04
F2
F2
F2
F1=Fsin
2.与F2相切,一个交点。
F1=Fsin时有唯一解
此时F2最小
1.与F2相交,两个交点。
即Fsin F时
有两解
3.与F2相离,无交点。
F1F2
4.与F2相离,无交点。
F1>F时唯一解。
合成与分解过程中求极值的问题
三个力合成的极值问题
F1
F2
F3
1.三力中F3是最大值,且F3> F1+ F2,
合成与分解过程中求极值的问题
三个力合成的极值问题
F1
F2
F3
1.三力中F3是最大值,且F3> F1+ F2,
最大值为F= F1+ F2+ F3,最小值为F= F3 -|F1+ F2|
F
F1
F2
F3
F
2.三力中F3是最大值,且F3≤ F1+ F2,
最大值为F= F1+ F2+ F3,最小值为0
F1
F2
F3
F
F1
F2
F3
合成与分解过程中求极值的问题
三个在分解中的极值问题
1.已知合力F的大小、方向和一个分力F1的方向时,求另一个力的最小值的条件是两个分力相互垂直。
>>04
F1
2.已知合力F的方向和一个分力F1的大小、方向时,求另一个力的最小值的条件是分力与合力相互垂直,大小为F2=Fsin
F1
合成与分解过程中求极值的问题
三个在分解中的极值问题
1.已知合力F的大小、方向和一个分力F1的方向时,求另一个力的最小值的条件是两个分力相互垂直。
>>04
F1
3.已知合力F的大小及一个分力F1的大小时,求另一个力的最小值的条件是已知分力F1与合力F同向 ,最小分力F2=|F-F1|。
盛大私服
3.4拓展
力的合成和分解
一、两个共点力的合力求解
NUMBER.
>>01
所有情况适用——公式法
作图之后可以根据力的图示法做出力的标度,根据力的标度去度量对角线的长度,长度就代表合力的大小。
一、两个共点力的合力求解
NUMBER.
>>01
所有情况适用——公式法
一、当F1和F2不变。 在增大而减小。
0
A
C
B
D
AD=OB
AD=AC
F2
F1
F合
AD=F2
CD=F2
=
=
=
一、当F1和F2不变。 在增大而减小。
|F1-F1|≤F合≤ F1+F1
一、两个共点力的合力求解
NUMBER.
>>01
所有情况适用
0
F2
F1
F合
=
一、两个共点力的合力求解
NUMBER.
>>02
垂直用勾股
0
F2
F1
F合
=
一、两个共点力的合力求解
NUMBER.
>>02
两力相等角度为
0
F2
F1
F合
F合=2F1cos
1.当=60°时, F合=
2.当=90°时, F合=
3.当=120°时, F合=
一、两个共点力的合力求解
平行四边形的一半就是三角形,在求合力时,将原来的两个共点力首位相接,则第一个力的起点向第二个力的末端画一矢量,这个矢量就是原来两个力的合力。
矢量三角形求合力
>>04
平行四边形的一半就是三角形,在求合力时,将原来的两个共点力首位相接,则第一个力的起点向第二个力的末端画一矢量,这个矢量就是原来两个力的合力。
始
末
F合
一、两个共点力的合力求解
矢量三角形求合力
二、多个共点力的合力求解
先利用平行四边形法则合成两个力,在将合成的力与第三个力合成。以此类推。
F合
F2
平行四边形法则
>>04
F1
F3
二、多个共点力的合力求解
在求多力合力时,可以利用矢量三角形的方法求解,往往会结合几何关系来确定大小。
方法:依旧让共点力首位相连,第一个力开始端指向最后一个力末尾端的矢量就是合力。
F合
F2
矢量三角形法则
>>04
F1
F3
二、多个共点力的合力求解
F合
F2
>>04
F1
F3
F合
F2
F1
F3
在求多力合力时,可以利用矢量三角形的方法求解,往往会结合几何关系来确定大小。
方法:依旧让共点力首位相连,第一个力开始端指向最后一个力末尾端的矢量就是合力。
矢量三角形法则
在求多力合力时,可以利用矢量三角形的方法求解,往往会结合几何关系来确定大小。
方法:依旧让共点力首位相连,第一个力开始端指向最后一个力末尾端的矢量就是合力。
二、多个共点力的合力求解
>>04
矢量三角形法则
O
F1
F2
F3
F4
F5
在求多力合力时,可以利用矢量三角形的方法求解,往往会结合几何关系来确定大小。
方法:依旧让共点力首位相连,第一个力开始端指向最后一个力末尾端的矢量就是合力。
二、多个共点力的合力求解
>>04
矢量三角形法则
O
F1
F2
F3
F4
F5
在求多力合力时,可以利用矢量三角形的方法求解,往往会结合几何关系来确定大小。
方法:依旧让共点力首位相连,第一个力开始端指向最后一个力末尾端的矢量就是合力。
二、多个共点力的合力求解
>>04
矢量三角形法则
O
F合=3F3=30N
二、多个共点力的合力求解
>>04
F1
F3
在求多力合力时,可以利用矢量三角形的方法求解,往往会结合几何关系来确定大小。
方法:依旧让共点力首尾相连,第一个力开始端指向最后一个力末尾端的矢量就是合力。
矢量三角形法则
F2
F合
二、多个共点力的合力求解
>>04
F1
F3
在求多力合力时,可以利用矢量三角形的方法求解,往往会结合几何关系来确定大小。
方法:依旧让共点力首尾相连,第一个力开始端指向最后一个力末尾端的矢量就是合力。
矢量三角形法则
F2
F4
直接构成封闭图形,则合力为零。即共点力平衡。
F8
F8
F8= F1
F8= F1
F8= F1
F8
F8
F8
F8= F1
F8= F1
F8= F1
F8
2F1
2F1
F1
F1
F1
2F1
C
力的分解
力的分解是力的合成的逆过程,通常使用平行四边形法则、矢量三角形法则、正交分解等方法。
力的合成与分解是互为逆运算。
力的分解
>>04
平行四边形法则
F
F1
F2
三角形法则
>>02
F
F1
F2
力的分解
正交分解——最重要的方法
方法:
1.以共点力的作用点为坐标原点,画直角坐标系。
2.坐标系的画线原则让尽量多的力落在坐标轴上。
3.正交分解不在坐标轴上的力,使得分解的力落在xy轴上。
4.对x.y轴的力进行合成。
5.求最终合力。
F1
F2
F3
F4
x
y
F5
F6
三角函数知识的补充
正交分解——最重要的方法
方法:
1.以共点力的作用点为坐标原点,画指标坐标系。
2.坐标系的画线原则让尽量多的力落在坐标轴上。
3.正交分解不在坐标轴上的力,使得分解的力落在xy轴上。
4.对x.y轴的力进行合成。
5.求最终合力。
某同学为了研究三角形承重结构各部分受力大小的规律,设计如图
所示的装置:一长度 的轻质细杆, 端通过光滑铰链连接
于竖直墙上, 端系上轻质细绳,细绳水平,另一端系于竖直墙上 点,
点悬挂一质量为 的重物,该系统保持静止状态。
系统保持静止状态。已知此时细绳长度为 ,重力加速度 取 。
x
y
F1
F1
x
y
F1
F1
(1)求此时轻绳 和轻杆 受到的弹力大小。
解析: 点受力如图甲所示,设 为 ,
水平方向 ,
竖直方向 ,
解得 , 。
F1
(2)若保持细杆 位置不动,只改变轻绳 的长度及
点位置,要使系统静止且绳子承受的拉力最小,求此时
轻绳 的长度及所受拉力大小。
解析:当 绳与 杆垂直时受到的拉力最小,如图乙所示,
此时细绳 长度为
解得
细绳拉力
解得 。
F
一定条件下力的分解
无条件限制,无数种分解方法
已知合力F和两个分力的方向
F
唯一解
F1
F2
F
,但两分力不能共线,共线就有无数种解。
已知合力F和两个分力的大小
F1
F2
F
利用三角形法则,分力F1和F2首尾相接
一定条件下力的分解
无条件限制,无数种分解方法
已知合力F和两个分力的方向
F
唯一解
,但两分力不能共线,共线就有无数种解。
已知合力F和两个分力的大小
F1
F2
F
利用三角形法则,分力F1和F2首尾相接
F1
F2
1.两圆相交,两个交点。
即|F1-F1|≤F合≤ F1+F1
有两种分解方法
F1
F2
一定条件下力的分解
无条件限制,无数种分解方法
已知合力F和两个分力的方向
F
唯一解
,但两分力不能共线,共线就有无数种解。
已知合力F和两个分力的大小
F1
F2
F
利用三角形法则,分力F1和F2首尾相接
F1
F2
2.两圆相切,一个交点。
一定条件下力的分解
无条件限制,无数种分解方法
已知合力F和两个分力的方向
F
唯一解
,但两分力不能共线,共线就有无数种解。
已知合力F和两个分力的大小
F1
F2
F
利用三角形法则,分力F1和F2首尾相接
F1
F2
2.两圆相切,一个交点。
即|F1-F1|=F合或F合= F1+F1
有一种分解方法
一定条件下力的分解
无条件限制,无数种分解方法
已知合力F和两个分力的方向
F
唯一解
,但两分力不能共线,共线就有无数种解。
已知合力F和两个分力的大小
F1
F2
F
利用三角形法则,分力F1和F2首尾相接
F1
F2
2.两圆内含,无交点。
即|F1-F1|>F合无解
一定条件下力的分解
无条件限制,无数种分解方法
已知合力F和两个分力的方向
F
唯一解
,但两分力不能共线,共线就有无数种解。
已知合力F和两个分力的大小
F1
F2
F
利用三角形法则,分力F1和F2首尾相接
F1
F2
3.两圆相离,无交点。
即即|F1-F1|>F合
或F> F1+F1 无解
一定条件下力的分解
已知合力F和F1的大小以及F2的方向,若F与F2的夹角为
>>04
F2
F2
F2
F1=Fsin
2.与F2相切,一个交点。
F1=Fsin时有唯一解
此时F2最小
1.与F2相交,两个交点。
即Fsin F时
有两解
3.与F2相离,无交点。
F1
4.与F2相离,无交点。
F1>F时唯一解。
合成与分解过程中求极值的问题
三个力合成的极值问题
F1
F2
F3
1.三力中F3是最大值,且F3> F1+ F2,
合成与分解过程中求极值的问题
三个力合成的极值问题
F1
F2
F3
1.三力中F3是最大值,且F3> F1+ F2,
最大值为F= F1+ F2+ F3,最小值为F= F3 -|F1+ F2|
F
F1
F2
F3
F
2.三力中F3是最大值,且F3≤ F1+ F2,
最大值为F= F1+ F2+ F3,最小值为0
F1
F2
F3
F
F1
F2
F3
合成与分解过程中求极值的问题
三个在分解中的极值问题
1.已知合力F的大小、方向和一个分力F1的方向时,求另一个力的最小值的条件是两个分力相互垂直。
>>04
F1
2.已知合力F的方向和一个分力F1的大小、方向时,求另一个力的最小值的条件是分力与合力相互垂直,大小为F2=Fsin
F1
合成与分解过程中求极值的问题
三个在分解中的极值问题
1.已知合力F的大小、方向和一个分力F1的方向时,求另一个力的最小值的条件是两个分力相互垂直。
>>04
F1
3.已知合力F的大小及一个分力F1的大小时,求另一个力的最小值的条件是已知分力F1与合力F同向 ,最小分力F2=|F-F1|。
