物理人教版(2019)选择性必修第一册1.5弹性碰撞和非弹性碰撞(共28张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册1.5弹性碰撞和非弹性碰撞(共28张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 62.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-02 13:23:47 | ||
图片预览








文档简介
(共28张PPT)
1.5 弹性碰撞和非弹性碰撞
第一章 动量守恒定律
超弹性碰撞球实验
思考与讨论:
2.实验时,为什么将球叠放在一起,最上面的球就能被弹到很高的位置?
1.小球被弹的很高,说明小球具有的能量大小如何?
为了解释这样一个问题,那么这节课我们将从能量的角度来继续研究碰撞问题。
一、弹性碰撞和非弹性碰撞
1.实验
演示:
一、弹性碰撞和非弹性碰撞
2.数据处理(环节一:质量不同装有弹性碰撞架的滑块发生碰撞后分开)
质量m(g) 速度v(cm/s) 总动能(J) 次数 A滑块m1 B滑块m2 A碰前v1 B碰前v2 A碰后v'1 B碰后v'2 碰前 碰后
1 275.5 175.5 56.0 0 12.8 67.3 0.043 0.042
2 74.7 0 16.5 89.2 0.076 0.074
3 92.0 0 22.7 108.3 0.116 0.110
3.实验结论:
环节一:在实验误差范围内,两个滑块组成的系统在碰撞前后动能不变,将这类碰撞叫弹性碰撞;
一、弹性碰撞和非弹性碰撞
2.数据处理(环节二:质量不同且贴有胶布的滑块发生碰撞后不分开)
质量m(g) 速度v(cm/s) 总动能(J) 次数 A滑块m1 B滑块m2 A碰前v1 B碰前v2 A碰后v'1 B碰后v'2 碰前 碰后
1 270.0 168.0 79.0 0 45.8 45.8 0.084 0.048
2 89.0 0 54.1 54.1 0.107 0.068
3 142.4 0 87.4 87.4 0.274 0.174
3.实验结论:
环节二:在实验误差范围内,两个滑块组成的系统在碰撞后动能减少,将这类碰撞叫非弹性碰撞。
一、弹性碰撞和非弹性碰撞
1.弹性碰撞:
(2)特点:①系统动量守恒;②机械能守恒
(3)规律:
①动量守恒:
②机械能守恒:
(1)定义:碰撞过程中机械能守恒的碰撞。
一、弹性碰撞和非弹性碰撞
(3)规律:
①动量守恒
完全非弹性碰撞:机械能损失最多
②机械能有损失
或者
动量守恒
机械能损失最大
2.非弹性碰撞:
(1)定义:碰撞过程中机械能不守恒的碰撞。
(2)特点:①系统动量守恒;②机械能不守恒
一、弹性碰撞和非弹性碰撞
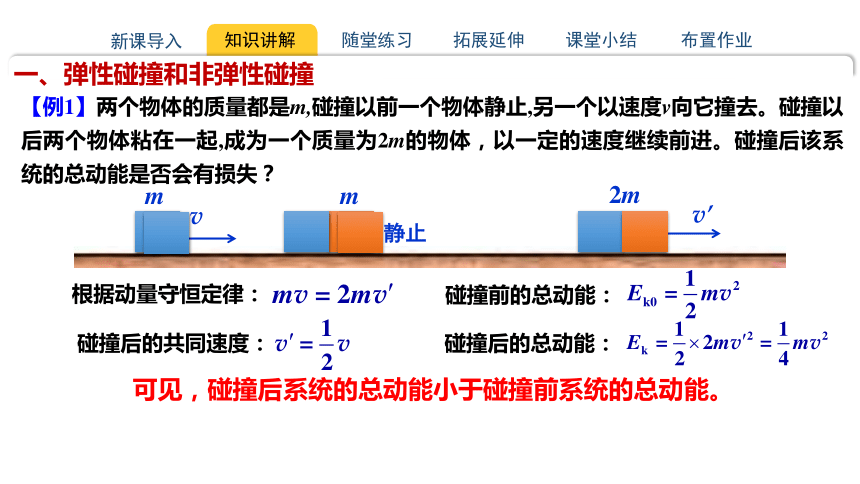
【例1】两个物体的质量都是m,碰撞以前一个物体静止,另一个以速度v向它撞去。碰撞以后两个物体粘在一起,成为一个质量为2m的物体,以一定的速度继续前进。碰撞后该系统的总动能是否会有损失?
v
静止
m
m
v’
2m
根据动量守恒定律:
碰撞后的共同速度:
碰撞前的总动能:
碰撞后的总动能:
可见,碰撞后系统的总动能小于碰撞前系统的总动能。
v1
静止
m1
m2
v2’
m2
根据动量守恒定律:
弹性碰撞机械能守恒:
碰撞后两个物体的速度:
1.动碰静: 物体m1以速度v1与原来静止的物体m2发生弹性碰撞,碰撞后它们的速度分别为v1' 和v2' 。用m1、m2、v1表示v1' 和v2' 的公式。
v1’
m1
二、弹性碰撞的实例分析
【例2】速度为10m/s的塑料球与静止的钢球发生正碰,钢球的质量是塑料球的4倍,碰撞是弹性的,求碰撞后两个小球的速度.
解:由于是弹性碰撞,根据动量守恒和机械能守恒得
塑料球:
钢球:
与塑料球初速度方向相反
与塑料球初速度方向相同
二、弹性碰撞的实例分析
碰撞后两个物体的速度:
二、弹性碰撞的实例分析
结论:
碰后实现动量和动能的全部转移(即交换了速度)
碰后m1速度几乎没变,仍按原速度运动 ,质量小物体以m1的速度的两倍向前运动。
碰后m1被按原来速率弹回,m2几乎末动。
1.m1=m2时
2.m1>>m2时
3.m1<4.m1>m2时v1′>0,v2 ′>0, 碰撞后两球都向前运动.
5.m1<m2时v1 ′<0,v2 ′>0,碰撞后质量小的球被反弹回去.
碰撞过程中系统动量守恒:
弹性碰撞中没有机械能损失:
若v2=0时,结论与前面的是否相同?
2.动碰动:若在一光滑水平面上有两个质量分别为m1、m2的刚性小球A和B,以初速度v1、v2运动,若它们能发生碰撞(为一维弹性碰撞),碰撞后它们的速度分别为v'1和v'2分别是多大?
碰撞后两个物体的速度:
二、弹性碰撞的实例分析(选讲)
3、碰撞三原则:
(1)动量守恒:即p1+p2=p1′+p2′.
(2)动能不增加:即Ek1+Ek2 ≥ Ek1′+Ek2′.
(3)速度要合理
①若碰前两物体同向运动,则应有v后 > v前,碰后原来在前的物体速度一定增大,若碰后两物体同向运动,则应有v前′ ≥ v后′。
②碰前两物体相向运动,碰后两物体的运动方向不可能都不改变。
二、弹性碰撞的实例分析
【例3】质量相等的 A、B 两球在光滑水平桌面上沿同一直线、同一方向运动,A 球的动量是 7 kg·m/s,B 球的动量是 5 kg·m/s, A 球追上 B 球发生碰撞,碰撞后两球的动量可能值是( )
A. pA = 6 kg·m/s, pB' = 6 kg·m/s
B. pA = 3 kg·m/s, pB' = 9 kg·m/s
C. pA =2 kg·m/s, pB' = 14 kg·m/s
D. pA = 4 kg·m/s,pB' = 17 kg·m/s
A
分析讲解:
碰撞过程动量守恒,
知:A、B、C都满足.
,知:A、B、C也都满足.
总动能不能增加,即
得:只有A正确了
三、碰撞的其他常见实例----碰撞中弹簧模型
1.弹簧处于最长(最短)状态时,两物体速度相等,弹性势能最大:
(1)动量守恒:
(2)最大弹性势能:
2.弹簧处于原长时,弹性势能为零,动能守恒:
(1)动量守恒:
(2)动能守恒:
例题4、如图甲所示,一轻弹簧的两端与质量分别为m1和m2的两物块A、B相连接,并静止在光滑的水平面上。现使A瞬时获得水平向右的速度3m/s,以此刻为计时起点,两物块的速度随时间变化的规律如图乙所示,从图像信息可得( )
A.在t1、t3时刻两物块达到共同速度1m/s,且弹簧都是处于压缩状态
B.从t3到t4时刻弹簧由压缩状态恢复到原长
C.两物体的质量之比为m1:m2=1:2
D.在t2时刻A与B的动能之比为Ek1:Ek2=1:8
CD
例题5、质量均为m的A、B两球,一轻弹簧连接后放在光滑水平面上,A被一水平速度为v0,质量为m/4的泥丸P击中并粘合,求损失的机械能和弹簧能具有的最大势能。
P与A碰撞,有动量守恒:
得v1= 1/5v①
解析:
P、A与B作用,有动量守恒:(m/4+m)v1=(m+m/4+m)v2 ②
(或全过程,有动量守恒:m/4v0=(m+m/4+m)v2 ③
所损失的机械能在P与A碰撞中,
由机械能(或由能量)守恒得:弹簧具有的最大弹性势能为EP
④
由①-④得: EP=
1.模型特点
(1)模型图
(2)模型特点
最高点:m与M有共同的水平速度,且m不可能从此处离开轨道,系统水平方向动量守恒,系统机械能守恒。
②m与M分离点,水平方向上动量守恒,系统机械能守恒
v0
m
M
三、碰撞的其他常见实例----滑块—圆弧槽(斜面)模型
例题6、如图所示,光滑水平面上质量为m1=2kg的物块以v0=2m/s的初速度冲向质量为m2=6kg静止的光滑圆弧面斜劈体。求:
(1)物块m1滑到最高点位置时,二者的速度;
(2)物块m1从圆弧面滑下后,二者速度
(3)若m1= m2物块m1从圆弧面滑下后,二者速度
v0
m2
m1
解:(1)由动量守恒得
m1V0=(m1+m2)V
V=m1V0/(m1+m2)=0.5m/s
(2)由弹性碰撞公式
(3)质量相等的两物体弹性碰撞后交换速度
∴ v1 = 0 v2=2m/s
三、碰撞的其他常见实例----板块模型
M
m
v0
x
S
f
f
v
结论:系统动量守恒
木板放在光滑的水平地面上
根据动量定理
M
m
v0
x
S
f
f
v
根据牛顿第二定律
三、碰撞的其他常见实例----板块模型
木板放在光滑的水平地面上
结论:机械能的减少量等于摩擦力与相对位移的积
M
m
v0
x
S
f
f
v
三、碰撞的其他常见实例----板块模型
木板放在光滑的水平地面上
【例7】如图所示,长木板A放在光滑的水平面上,质量为m=4kg的小物体B以水平速度v0=2m/s滑上原来静止的长木板A的表面,由于A、B间存在摩擦,之后A、B速度随时间变化情况如图乙所示,取g=10m/s2,则下列说法正确的是( )
A.木板A获得的动能为2J
B.系统损失的机械能为2J
C.木板A的最小长度为2m
D.A、B间的动摩擦因数为0.1
AD
弹性碰撞和
非弹性碰撞
弹性碰撞
非弹性碰撞
①动量守恒:
②机械能不守恒:
①动碰静
②动碰动
练习1、在气垫导轨上,一个质量为400g的滑块以15cm/s的速度与另一个质量为200g,速度为10cm/s并沿反方向运动的滑块迎面相撞,碰撞后两个滑块粘在一起。
(1)求碰撞后滑块速度的大小和方向.
(2)这次碰撞,两滑块共损失了多少机械能?
解:(1)以400g的滑块的初速度方向为正方向,根据动量守恒定律
(2)损失的机械能:
练习2、一 种未知粒子跟静止的氢原子核正碰,测出碰撞后氢原子核的速度3.3×107m/s.该未知粒子跟静止的氮原子核正碰时,测出碰撞后氮原子核的速度是4.4×106m/s.已知氢原子核的质量是mH,氮原子核的质量是14mH,上述碰撞都是弹性碰撞,求未知粒子的质量.中子的质量与氢原子核的质量mH有什么关系.
【查德威克发现中子实验】
碰后氮原子核的速度为:
解:设未知粒子质量m,速度v,它与氢和氮原子核碰撞都是弹性的,碰后氢原子核的速度为:
两式联立,解得未知粒子的质量为mH
练习3、如图甲所示,在光滑水平面上的两小球发生正碰。小球的质量分别为 m1 和 m2。图乙为它们碰撞前后的 s t (位移 ─ 时间) 图象。已知 m1 = 0.1 kg。由此可以判断 ( )
AC
A. 碰前 m2 静止,m1 向右运动
B. 碰后 m2 和 m1 都向右运动
C. m2 = 0.3 kg
D. 碰撞过程中系统损失了 0.4 J 的机械能
1.5 弹性碰撞和非弹性碰撞
第一章 动量守恒定律
超弹性碰撞球实验
思考与讨论:
2.实验时,为什么将球叠放在一起,最上面的球就能被弹到很高的位置?
1.小球被弹的很高,说明小球具有的能量大小如何?
为了解释这样一个问题,那么这节课我们将从能量的角度来继续研究碰撞问题。
一、弹性碰撞和非弹性碰撞
1.实验
演示:
一、弹性碰撞和非弹性碰撞
2.数据处理(环节一:质量不同装有弹性碰撞架的滑块发生碰撞后分开)
质量m(g) 速度v(cm/s) 总动能(J) 次数 A滑块m1 B滑块m2 A碰前v1 B碰前v2 A碰后v'1 B碰后v'2 碰前 碰后
1 275.5 175.5 56.0 0 12.8 67.3 0.043 0.042
2 74.7 0 16.5 89.2 0.076 0.074
3 92.0 0 22.7 108.3 0.116 0.110
3.实验结论:
环节一:在实验误差范围内,两个滑块组成的系统在碰撞前后动能不变,将这类碰撞叫弹性碰撞;
一、弹性碰撞和非弹性碰撞
2.数据处理(环节二:质量不同且贴有胶布的滑块发生碰撞后不分开)
质量m(g) 速度v(cm/s) 总动能(J) 次数 A滑块m1 B滑块m2 A碰前v1 B碰前v2 A碰后v'1 B碰后v'2 碰前 碰后
1 270.0 168.0 79.0 0 45.8 45.8 0.084 0.048
2 89.0 0 54.1 54.1 0.107 0.068
3 142.4 0 87.4 87.4 0.274 0.174
3.实验结论:
环节二:在实验误差范围内,两个滑块组成的系统在碰撞后动能减少,将这类碰撞叫非弹性碰撞。
一、弹性碰撞和非弹性碰撞
1.弹性碰撞:
(2)特点:①系统动量守恒;②机械能守恒
(3)规律:
①动量守恒:
②机械能守恒:
(1)定义:碰撞过程中机械能守恒的碰撞。
一、弹性碰撞和非弹性碰撞
(3)规律:
①动量守恒
完全非弹性碰撞:机械能损失最多
②机械能有损失
或者
动量守恒
机械能损失最大
2.非弹性碰撞:
(1)定义:碰撞过程中机械能不守恒的碰撞。
(2)特点:①系统动量守恒;②机械能不守恒
一、弹性碰撞和非弹性碰撞
【例1】两个物体的质量都是m,碰撞以前一个物体静止,另一个以速度v向它撞去。碰撞以后两个物体粘在一起,成为一个质量为2m的物体,以一定的速度继续前进。碰撞后该系统的总动能是否会有损失?
v
静止
m
m
v’
2m
根据动量守恒定律:
碰撞后的共同速度:
碰撞前的总动能:
碰撞后的总动能:
可见,碰撞后系统的总动能小于碰撞前系统的总动能。
v1
静止
m1
m2
v2’
m2
根据动量守恒定律:
弹性碰撞机械能守恒:
碰撞后两个物体的速度:
1.动碰静: 物体m1以速度v1与原来静止的物体m2发生弹性碰撞,碰撞后它们的速度分别为v1' 和v2' 。用m1、m2、v1表示v1' 和v2' 的公式。
v1’
m1
二、弹性碰撞的实例分析
【例2】速度为10m/s的塑料球与静止的钢球发生正碰,钢球的质量是塑料球的4倍,碰撞是弹性的,求碰撞后两个小球的速度.
解:由于是弹性碰撞,根据动量守恒和机械能守恒得
塑料球:
钢球:
与塑料球初速度方向相反
与塑料球初速度方向相同
二、弹性碰撞的实例分析
碰撞后两个物体的速度:
二、弹性碰撞的实例分析
结论:
碰后实现动量和动能的全部转移(即交换了速度)
碰后m1速度几乎没变,仍按原速度运动 ,质量小物体以m1的速度的两倍向前运动。
碰后m1被按原来速率弹回,m2几乎末动。
1.m1=m2时
2.m1>>m2时
3.m1<
5.m1<m2时v1 ′<0,v2 ′>0,碰撞后质量小的球被反弹回去.
碰撞过程中系统动量守恒:
弹性碰撞中没有机械能损失:
若v2=0时,结论与前面的是否相同?
2.动碰动:若在一光滑水平面上有两个质量分别为m1、m2的刚性小球A和B,以初速度v1、v2运动,若它们能发生碰撞(为一维弹性碰撞),碰撞后它们的速度分别为v'1和v'2分别是多大?
碰撞后两个物体的速度:
二、弹性碰撞的实例分析(选讲)
3、碰撞三原则:
(1)动量守恒:即p1+p2=p1′+p2′.
(2)动能不增加:即Ek1+Ek2 ≥ Ek1′+Ek2′.
(3)速度要合理
①若碰前两物体同向运动,则应有v后 > v前,碰后原来在前的物体速度一定增大,若碰后两物体同向运动,则应有v前′ ≥ v后′。
②碰前两物体相向运动,碰后两物体的运动方向不可能都不改变。
二、弹性碰撞的实例分析
【例3】质量相等的 A、B 两球在光滑水平桌面上沿同一直线、同一方向运动,A 球的动量是 7 kg·m/s,B 球的动量是 5 kg·m/s, A 球追上 B 球发生碰撞,碰撞后两球的动量可能值是( )
A. pA = 6 kg·m/s, pB' = 6 kg·m/s
B. pA = 3 kg·m/s, pB' = 9 kg·m/s
C. pA =2 kg·m/s, pB' = 14 kg·m/s
D. pA = 4 kg·m/s,pB' = 17 kg·m/s
A
分析讲解:
碰撞过程动量守恒,
知:A、B、C都满足.
,知:A、B、C也都满足.
总动能不能增加,即
得:只有A正确了
三、碰撞的其他常见实例----碰撞中弹簧模型
1.弹簧处于最长(最短)状态时,两物体速度相等,弹性势能最大:
(1)动量守恒:
(2)最大弹性势能:
2.弹簧处于原长时,弹性势能为零,动能守恒:
(1)动量守恒:
(2)动能守恒:
例题4、如图甲所示,一轻弹簧的两端与质量分别为m1和m2的两物块A、B相连接,并静止在光滑的水平面上。现使A瞬时获得水平向右的速度3m/s,以此刻为计时起点,两物块的速度随时间变化的规律如图乙所示,从图像信息可得( )
A.在t1、t3时刻两物块达到共同速度1m/s,且弹簧都是处于压缩状态
B.从t3到t4时刻弹簧由压缩状态恢复到原长
C.两物体的质量之比为m1:m2=1:2
D.在t2时刻A与B的动能之比为Ek1:Ek2=1:8
CD
例题5、质量均为m的A、B两球,一轻弹簧连接后放在光滑水平面上,A被一水平速度为v0,质量为m/4的泥丸P击中并粘合,求损失的机械能和弹簧能具有的最大势能。
P与A碰撞,有动量守恒:
得v1= 1/5v①
解析:
P、A与B作用,有动量守恒:(m/4+m)v1=(m+m/4+m)v2 ②
(或全过程,有动量守恒:m/4v0=(m+m/4+m)v2 ③
所损失的机械能在P与A碰撞中,
由机械能(或由能量)守恒得:弹簧具有的最大弹性势能为EP
④
由①-④得: EP=
1.模型特点
(1)模型图
(2)模型特点
最高点:m与M有共同的水平速度,且m不可能从此处离开轨道,系统水平方向动量守恒,系统机械能守恒。
②m与M分离点,水平方向上动量守恒,系统机械能守恒
v0
m
M
三、碰撞的其他常见实例----滑块—圆弧槽(斜面)模型
例题6、如图所示,光滑水平面上质量为m1=2kg的物块以v0=2m/s的初速度冲向质量为m2=6kg静止的光滑圆弧面斜劈体。求:
(1)物块m1滑到最高点位置时,二者的速度;
(2)物块m1从圆弧面滑下后,二者速度
(3)若m1= m2物块m1从圆弧面滑下后,二者速度
v0
m2
m1
解:(1)由动量守恒得
m1V0=(m1+m2)V
V=m1V0/(m1+m2)=0.5m/s
(2)由弹性碰撞公式
(3)质量相等的两物体弹性碰撞后交换速度
∴ v1 = 0 v2=2m/s
三、碰撞的其他常见实例----板块模型
M
m
v0
x
S
f
f
v
结论:系统动量守恒
木板放在光滑的水平地面上
根据动量定理
M
m
v0
x
S
f
f
v
根据牛顿第二定律
三、碰撞的其他常见实例----板块模型
木板放在光滑的水平地面上
结论:机械能的减少量等于摩擦力与相对位移的积
M
m
v0
x
S
f
f
v
三、碰撞的其他常见实例----板块模型
木板放在光滑的水平地面上
【例7】如图所示,长木板A放在光滑的水平面上,质量为m=4kg的小物体B以水平速度v0=2m/s滑上原来静止的长木板A的表面,由于A、B间存在摩擦,之后A、B速度随时间变化情况如图乙所示,取g=10m/s2,则下列说法正确的是( )
A.木板A获得的动能为2J
B.系统损失的机械能为2J
C.木板A的最小长度为2m
D.A、B间的动摩擦因数为0.1
AD
弹性碰撞和
非弹性碰撞
弹性碰撞
非弹性碰撞
①动量守恒:
②机械能不守恒:
①动碰静
②动碰动
练习1、在气垫导轨上,一个质量为400g的滑块以15cm/s的速度与另一个质量为200g,速度为10cm/s并沿反方向运动的滑块迎面相撞,碰撞后两个滑块粘在一起。
(1)求碰撞后滑块速度的大小和方向.
(2)这次碰撞,两滑块共损失了多少机械能?
解:(1)以400g的滑块的初速度方向为正方向,根据动量守恒定律
(2)损失的机械能:
练习2、一 种未知粒子跟静止的氢原子核正碰,测出碰撞后氢原子核的速度3.3×107m/s.该未知粒子跟静止的氮原子核正碰时,测出碰撞后氮原子核的速度是4.4×106m/s.已知氢原子核的质量是mH,氮原子核的质量是14mH,上述碰撞都是弹性碰撞,求未知粒子的质量.中子的质量与氢原子核的质量mH有什么关系.
【查德威克发现中子实验】
碰后氮原子核的速度为:
解:设未知粒子质量m,速度v,它与氢和氮原子核碰撞都是弹性的,碰后氢原子核的速度为:
两式联立,解得未知粒子的质量为mH
练习3、如图甲所示,在光滑水平面上的两小球发生正碰。小球的质量分别为 m1 和 m2。图乙为它们碰撞前后的 s t (位移 ─ 时间) 图象。已知 m1 = 0.1 kg。由此可以判断 ( )
AC
A. 碰前 m2 静止,m1 向右运动
B. 碰后 m2 和 m1 都向右运动
C. m2 = 0.3 kg
D. 碰撞过程中系统损失了 0.4 J 的机械能
