高中数学 1.5《函数y=Asin(ωx φ)的图象》课件
文档属性
| 名称 | 高中数学 1.5《函数y=Asin(ωx φ)的图象》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 232.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-23 20:16:23 | ||
图片预览



文档简介
课件15张PPT。1.5函数y=Asin(ωx+φ)的图象教学目的:
1、理解振幅变换和周期变换和平移变换;会用图象变换的方法画y=Asin(ωx+ )的图象 ;
2、会用“五点法”画y=Asin(ωx+ )的图象 ;
3、会求一些函数的振幅、周期、最值等 ;
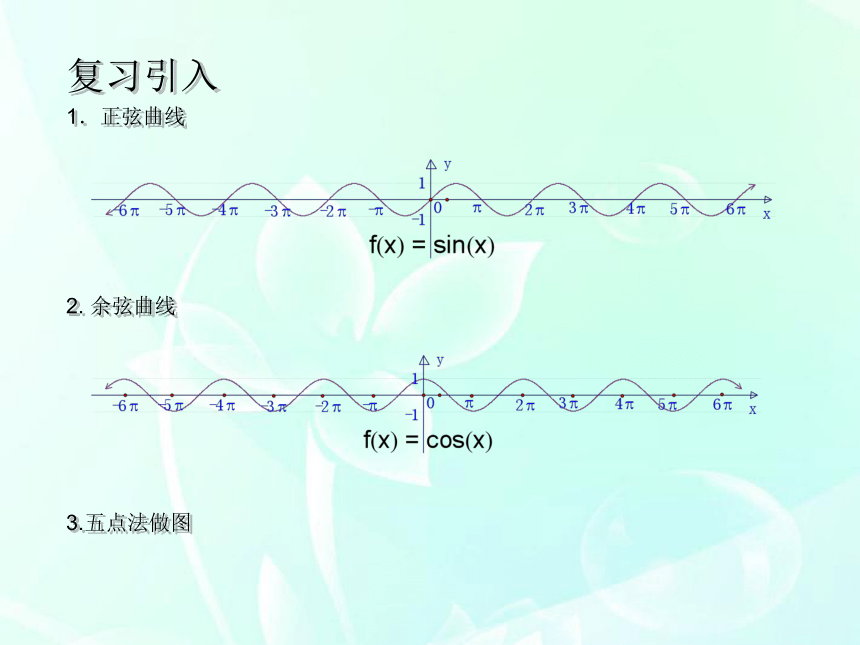
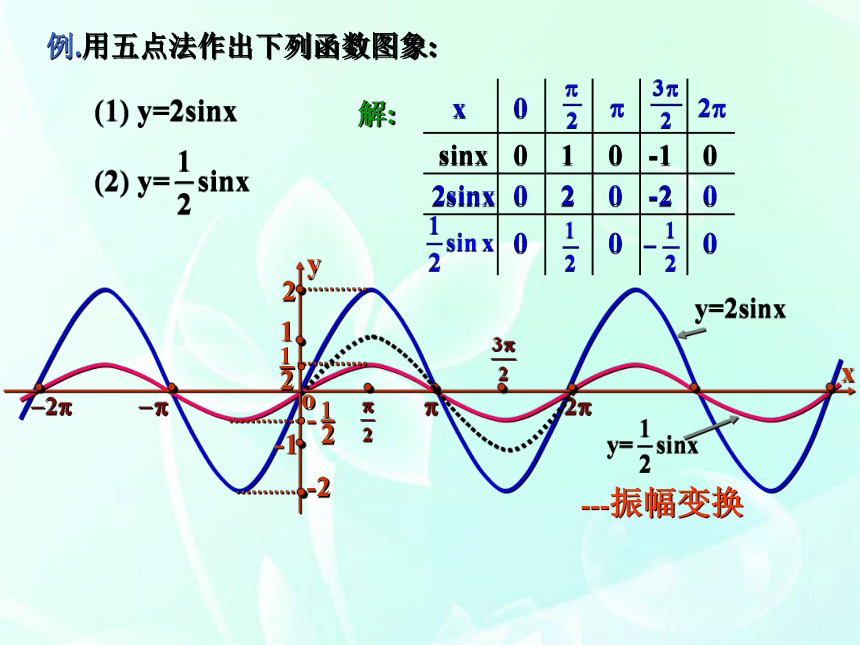
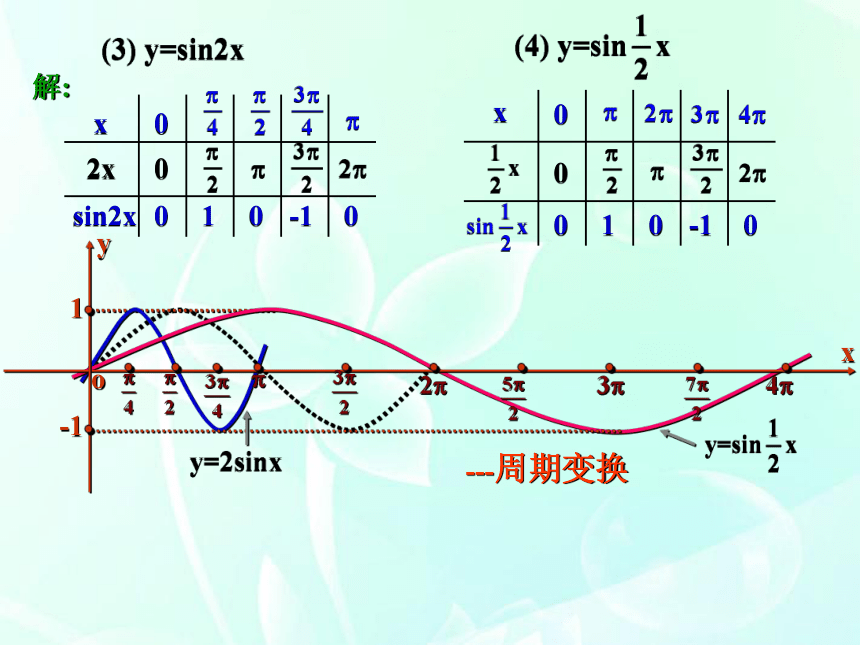
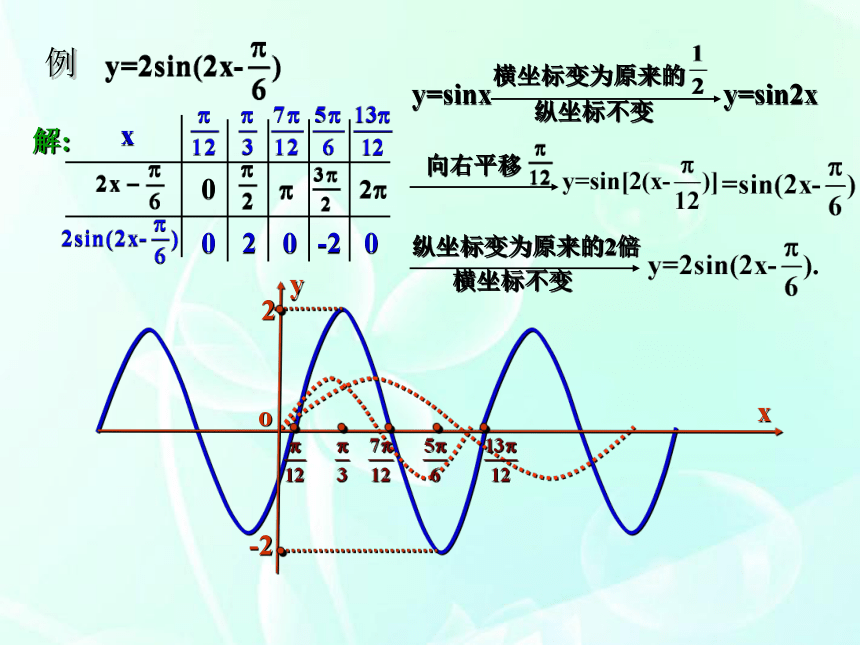
4、渗透分类讨论的数学思想,提高分析和解决问题的能力 。教学重点、难点:难点:理解振幅变换和周期变换和平移变换 。 重点:用图象变换的方法画y=Asin(ωx+ )的图象 。 复习引入 1.正弦曲线2. 余弦曲线3.五点法做图例.用五点法作出下列函数图象:解:xsinx2sinx001-100020-20000---振幅变换解:2xsin2x001-100x0001-100x0---周期变换解:002-200xy=sinxy=sin2x例小结:1.对于函数 y=Asin(?x+?) (A>0, ?>0):A --- 振幅,--- 周期,--- 频率,?x+? --- 相位,? --- 初相.2.图象的变换:(1)伸缩变换振幅变换周期变换(2)平移变换上下平移左右平移( ----- 形状变换)( ----- 位置变换)y=sinxy=sin(x+?)y=sin(?x+?)y=Asin(?x+?)?y=Asin(?x+?) (A>0, ?>0) 的图象可由y=sinx经过如下变换得到:y=sinxy=sin(x+?)y=sin(?x+?)y=Asin(?x+?)?或:y=sinxy=sin?xy=Asin(?x+?)=sin(?x+?) 解法1: 解法2: 解:(1)列表(2)描点
(3)用平滑的曲线顺次连结各点所得图象如图所示:
解:显然A=2
四、课堂练习P62练习题1、2、3、4、71.由解析式作图:
由函数y=Asin(?x+?)+B的解析式作图:
(1)五点作图法; (2)利用函数图象的变换.
2.看图识解析式:
抓住图象的特征,如关键点,周期,振幅,对称轴等.小结P65习题 A组第1、3题
B组 第2、3题六、课后作业:再见
1、理解振幅变换和周期变换和平移变换;会用图象变换的方法画y=Asin(ωx+ )的图象 ;
2、会用“五点法”画y=Asin(ωx+ )的图象 ;
3、会求一些函数的振幅、周期、最值等 ;
4、渗透分类讨论的数学思想,提高分析和解决问题的能力 。教学重点、难点:难点:理解振幅变换和周期变换和平移变换 。 重点:用图象变换的方法画y=Asin(ωx+ )的图象 。 复习引入 1.正弦曲线2. 余弦曲线3.五点法做图例.用五点法作出下列函数图象:解:xsinx2sinx001-100020-20000---振幅变换解:2xsin2x001-100x0001-100x0---周期变换解:002-200xy=sinxy=sin2x例小结:1.对于函数 y=Asin(?x+?) (A>0, ?>0):A --- 振幅,--- 周期,--- 频率,?x+? --- 相位,? --- 初相.2.图象的变换:(1)伸缩变换振幅变换周期变换(2)平移变换上下平移左右平移( ----- 形状变换)( ----- 位置变换)y=sinxy=sin(x+?)y=sin(?x+?)y=Asin(?x+?)?y=Asin(?x+?) (A>0, ?>0) 的图象可由y=sinx经过如下变换得到:y=sinxy=sin(x+?)y=sin(?x+?)y=Asin(?x+?)?或:y=sinxy=sin?xy=Asin(?x+?)=sin(?x+?) 解法1: 解法2: 解:(1)列表(2)描点
(3)用平滑的曲线顺次连结各点所得图象如图所示:
解:显然A=2
四、课堂练习P62练习题1、2、3、4、71.由解析式作图:
由函数y=Asin(?x+?)+B的解析式作图:
(1)五点作图法; (2)利用函数图象的变换.
2.看图识解析式:
抓住图象的特征,如关键点,周期,振幅,对称轴等.小结P65习题 A组第1、3题
B组 第2、3题六、课后作业:再见
