第五章 圆培优专题 圆中的最值问题同步练习(含答案)
文档属性
| 名称 | 第五章 圆培优专题 圆中的最值问题同步练习(含答案) | 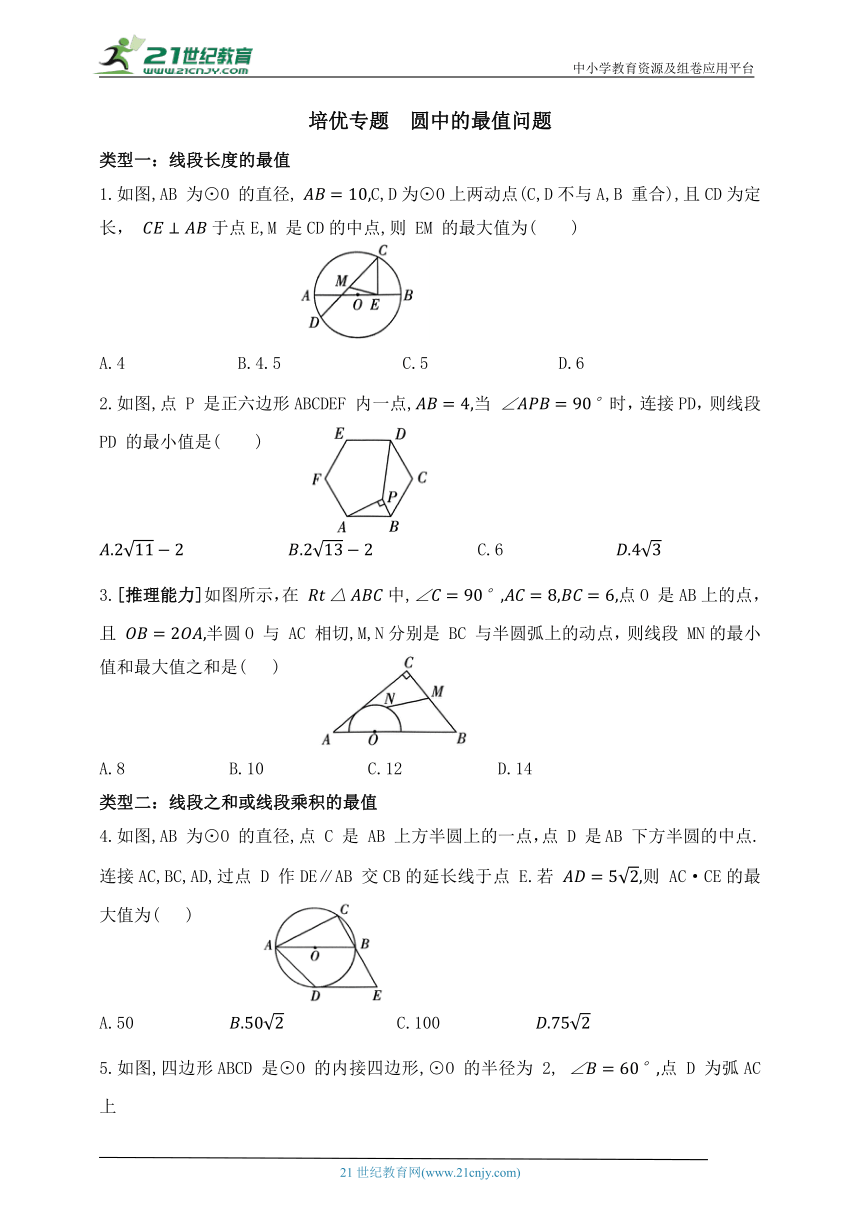 | |
| 格式 | docx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 11:45:54 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
培优专题 圆中的最值问题
类型一:线段长度的最值
1.如图,AB 为⊙O 的直径, C,D为⊙O上两动点(C,D不与A,B 重合),且CD为定长, 于点E,M 是CD的中点,则 EM 的最大值为( )
A.4 B.4.5 C.5 D.6
2.如图,点 P 是正六边形ABCDEF 内一点,当 时,连接PD,则线段
PD 的最小值是( )
C.6
3.[推理能力]如图所示,在 中,点O 是AB上的点,且 半圆O 与 AC 相切,M,N分别是 BC 与半圆弧上的动点,则线段 MN的最小值和最大值之和是( )
A.8 B.10 C.12 D.14
类型二:线段之和或线段乘积的最值
4.如图,AB 为⊙O 的直径,点 C 是 AB 上方半圆上的一点,点 D 是AB 下方半圆的中点.连接AC,BC,AD,过点 D 作DE∥AB 交CB的延长线于点 E.若 则 AC·CE的最大值为( )
A.50 C.100
5.如图,四边形ABCD 是⊙O 的内接四边形,⊙O 的半径为 2, 点 D 为弧AC上
的动点,点 M,N,P 分别是AD,DC,CB 的中点,则 的最大值为( )
类型三:周长或面积的最值
6.如图,在菱形ABCD 中, 以B为圆心,BC 的长为半径画弧AC,点 P为菱形内一动点,连接PA,PC,则阴影部分周长的最小值为__________.
7.如图,在平面直角坐标系xOy中,半径为2 的⊙O 与x轴的正半轴交于点A,点 B 是⊙O上一动点,点 C 为弦 AB 的中点,直线 与 x 轴、y 轴分别交于点 D,E,则 面积的最大值为___________.
参考答案
1. C
2. B [解析]∵AB=4,∠APB=90°,∴点 P 在以AB 为直径的圆弧上.如图,取 AB 的中点O,连接OD,当O,P,D三点共线时,PD有最小值,连接 BD,过点 C 作CH⊥BD于点H.∵点O为AB 的中点,∴OA=OB=OP=4÷2=2.∵正六边形的每个内角为 180°×(6-2)÷6=120°,CD=CB,∴∠CBD=(180°-120°)÷2 =30°,BD=2BH,∴∠OBD=120°-30°=90°.在 Rt△CBH 中, =2,BH=2 ,∴BD=4 .在 Rt△OBD 中,OD=∴PD的最小值为 OD-OP=
3. C [解析]如图,过点O 作OD⊥AC 于点D,OE⊥BC于点E,⊙O交AB 于点F,设⊙O 的半径为r.∵∠C=90°,∵AC 为切线,∴OD=OF=r.∵∠A此时MN的最小值为 ∴MN的最大值为 ∴MN的最小值和最大值之和
4. C
5. D [解析]如图,连接OC,OA,BD,AC,作于点H,则 , 当BD是直径时,PN的值最大,最大值为 2,∴PN的最大值为
7.7 [解析]如图,连接OC.∵点C 为弦AB 的中点,∴OC⊥AB,∴∠ACO=90°,∴点C 在以OA 为直径的圆上(点O,A 除外).以OA 为直径作⊙P,过点 P 作直线. DE 于点H,交⊙P 于点M,N.当x=0时, 则E(0,-3),当y=0时, 解得x=4,则D(4,0),∴OD=4,∴DE= +4 =5.∵A(2,0),∴P(1,0),∴OP=1,∴PD=OD-OP=3.∵∠PDH=∠EDO,∠PHD=∠EOD,∴△DPH∽△DEO,∴PH:OE=DP :DE,即 PH:3=3:5,解得 MH当C点与M点重合时,△CDE 面积的最大值为7.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
培优专题 圆中的最值问题
类型一:线段长度的最值
1.如图,AB 为⊙O 的直径, C,D为⊙O上两动点(C,D不与A,B 重合),且CD为定长, 于点E,M 是CD的中点,则 EM 的最大值为( )
A.4 B.4.5 C.5 D.6
2.如图,点 P 是正六边形ABCDEF 内一点,当 时,连接PD,则线段
PD 的最小值是( )
C.6
3.[推理能力]如图所示,在 中,点O 是AB上的点,且 半圆O 与 AC 相切,M,N分别是 BC 与半圆弧上的动点,则线段 MN的最小值和最大值之和是( )
A.8 B.10 C.12 D.14
类型二:线段之和或线段乘积的最值
4.如图,AB 为⊙O 的直径,点 C 是 AB 上方半圆上的一点,点 D 是AB 下方半圆的中点.连接AC,BC,AD,过点 D 作DE∥AB 交CB的延长线于点 E.若 则 AC·CE的最大值为( )
A.50 C.100
5.如图,四边形ABCD 是⊙O 的内接四边形,⊙O 的半径为 2, 点 D 为弧AC上
的动点,点 M,N,P 分别是AD,DC,CB 的中点,则 的最大值为( )
类型三:周长或面积的最值
6.如图,在菱形ABCD 中, 以B为圆心,BC 的长为半径画弧AC,点 P为菱形内一动点,连接PA,PC,则阴影部分周长的最小值为__________.
7.如图,在平面直角坐标系xOy中,半径为2 的⊙O 与x轴的正半轴交于点A,点 B 是⊙O上一动点,点 C 为弦 AB 的中点,直线 与 x 轴、y 轴分别交于点 D,E,则 面积的最大值为___________.
参考答案
1. C
2. B [解析]∵AB=4,∠APB=90°,∴点 P 在以AB 为直径的圆弧上.如图,取 AB 的中点O,连接OD,当O,P,D三点共线时,PD有最小值,连接 BD,过点 C 作CH⊥BD于点H.∵点O为AB 的中点,∴OA=OB=OP=4÷2=2.∵正六边形的每个内角为 180°×(6-2)÷6=120°,CD=CB,∴∠CBD=(180°-120°)÷2 =30°,BD=2BH,∴∠OBD=120°-30°=90°.在 Rt△CBH 中, =2,BH=2 ,∴BD=4 .在 Rt△OBD 中,OD=∴PD的最小值为 OD-OP=
3. C [解析]如图,过点O 作OD⊥AC 于点D,OE⊥BC于点E,⊙O交AB 于点F,设⊙O 的半径为r.∵∠C=90°,∵AC 为切线,∴OD=OF=r.∵∠A此时MN的最小值为 ∴MN的最大值为 ∴MN的最小值和最大值之和
4. C
5. D [解析]如图,连接OC,OA,BD,AC,作于点H,则 , 当BD是直径时,PN的值最大,最大值为 2,∴PN的最大值为
7.7 [解析]如图,连接OC.∵点C 为弦AB 的中点,∴OC⊥AB,∴∠ACO=90°,∴点C 在以OA 为直径的圆上(点O,A 除外).以OA 为直径作⊙P,过点 P 作直线. DE 于点H,交⊙P 于点M,N.当x=0时, 则E(0,-3),当y=0时, 解得x=4,则D(4,0),∴OD=4,∴DE= +4 =5.∵A(2,0),∴P(1,0),∴OP=1,∴PD=OD-OP=3.∵∠PDH=∠EDO,∠PHD=∠EOD,∴△DPH∽△DEO,∴PH:OE=DP :DE,即 PH:3=3:5,解得 MH当C点与M点重合时,△CDE 面积的最大值为7.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
