第五章 圆培优专题 求阴影部分面积的方法同步练习(含答案)
文档属性
| 名称 | 第五章 圆培优专题 求阴影部分面积的方法同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 8.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 11:46:54 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
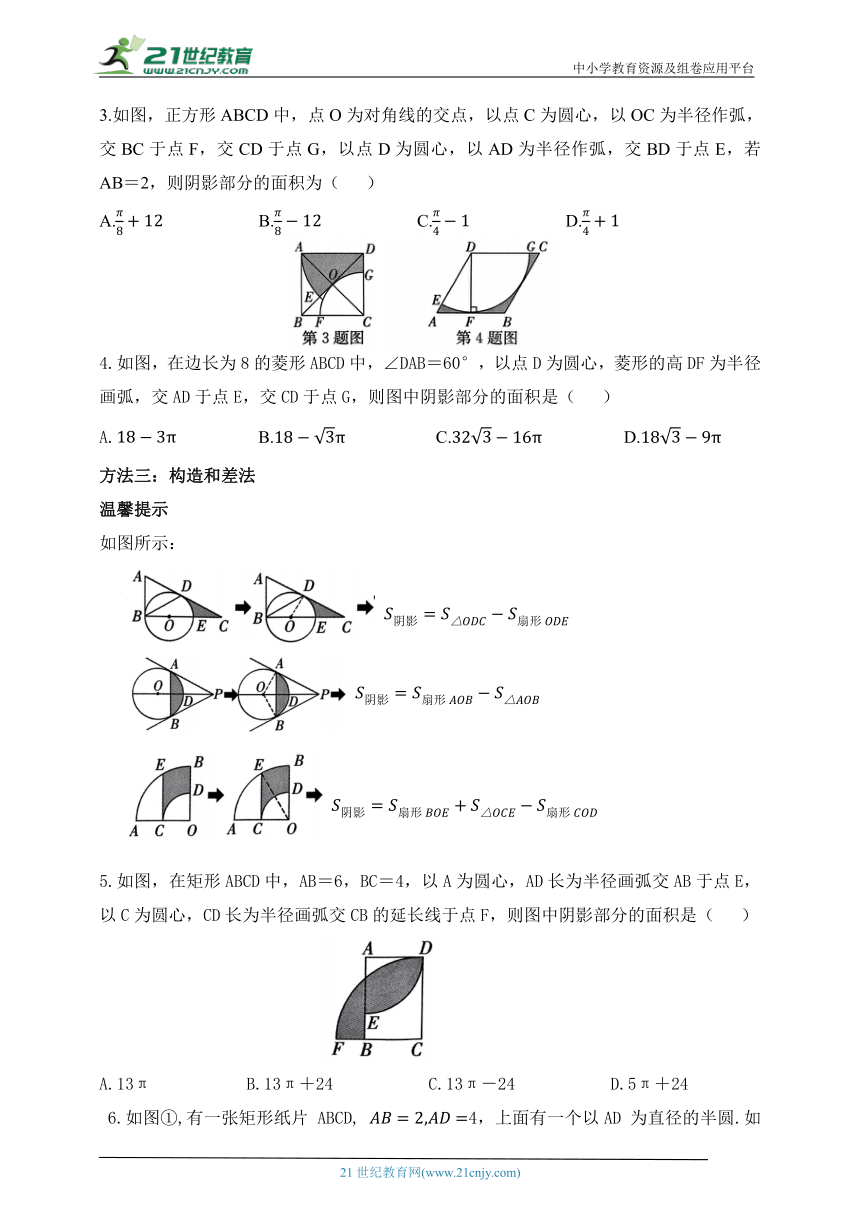
培优专题 求阴影部分面积的方法
方法一:公式法
温馨提示
如图所示,.
1.如图,菱形OABC的边长为,∠ABC=60°,以O为圆心,对角线OB为半径画弧分别交OA,OC的延长线于点D,E,则扇形DOE的面积为( )
A.π B.2π C.6π D.12π
2.如图,在Rt△ABC中,∠C=90°,CA=CB=4,分别以A,B,C为圆心,以AC为半径画弧,则阴影部分的面积是( )
A.4π B.8-π C.π D.2π
方法二:直接和差法
温馨提示
如图所示:
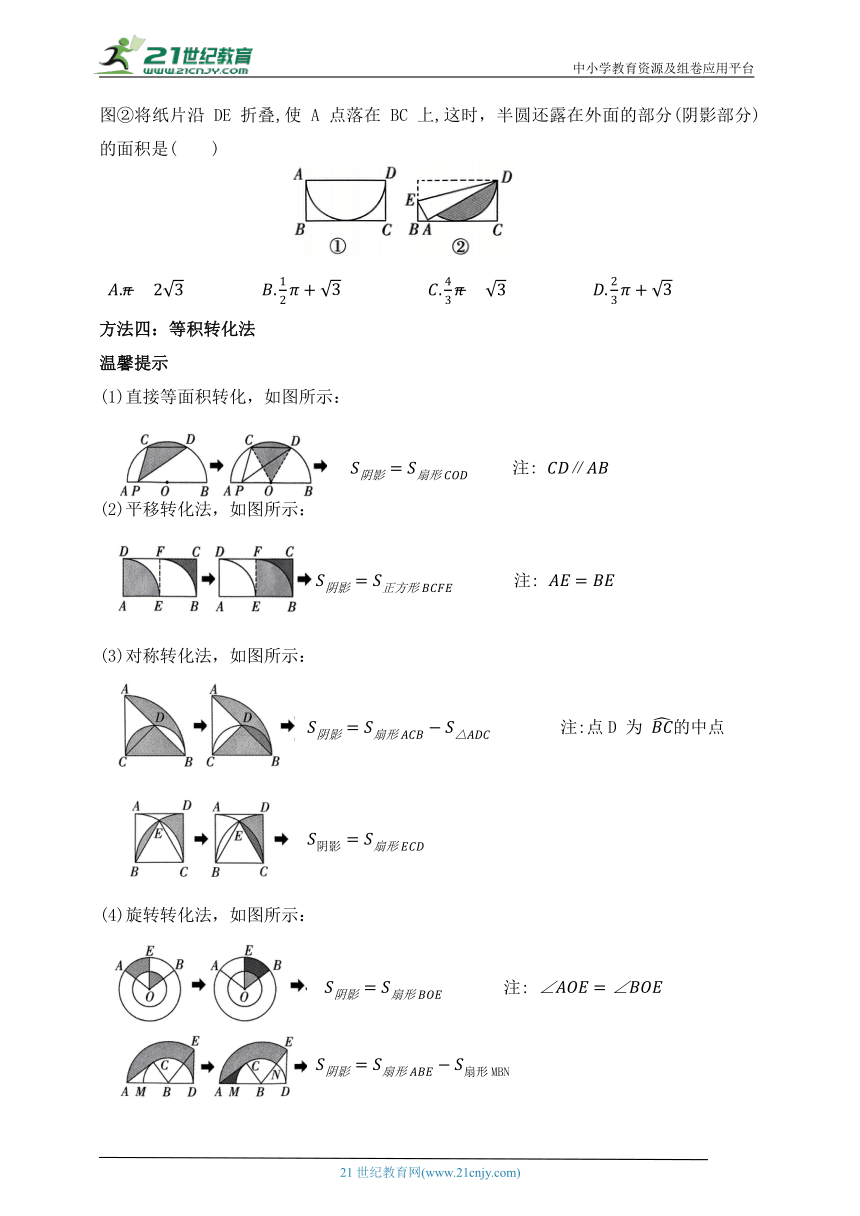
3.如图,正方形ABCD中,点O为对角线的交点,以点C为圆心,以OC为半径作弧,交BC于点F,交CD于点G,以点D为圆心,以AD为半径作弧,交BD于点E,若AB=2,则阴影部分的面积为( )
A. B. C. D.
4.如图,在边长为8的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是( )
A. B. C. D.
方法三:构造和差法
温馨提示
如图所示:
5.如图,在矩形ABCD中,AB=6,BC=4,以A为圆心,AD长为半径画弧交AB于点E,以C为圆心,CD长为半径画弧交CB的延长线于点F,则图中阴影部分的面积是( )
A.13π B.13π+24 C.13π-24 D.5π+24
6.如图①,有一张矩形纸片 ABCD, 4,上面有一个以AD 为直径的半圆.如图②将纸片沿 DE 折叠,使 A 点落在 BC 上,这时,半圆还露在外面的部分(阴影部分)的面积是( )
方法四:等积转化法
温馨提示
(1)直接等面积转化,如图所示:
注: ∥
(2)平移转化法,如图所示:
注:
(3)对称转化法,如图所示:
注:点D 为 的中点
(4)旋转转化法,如图所示:
注:
注:∠MEN=90°
7.如图,AB 为半圆O的直径,半径( 以OC 为直径的⊙D交AC 于点 E,交BC 于点 F,若 则图中阴影部分的面积为( )
A.2π-2 B.4π-2 C.4π-4 D.π-2
8.如图,正方形ABCD的边长为 4,分别以正方形的三边为直径在正方形内部作半圆,则阴影部分的面积之和是( )
A.8 B.4 C.16π D.4π
9.如图,在矩形ABCD 中,AB=6,BC=3,把以AB 为直径的半圆O绕点 B 顺时针旋转至如图位置(点 A 落在CD上的点 A处),则半圆O扫过的面积(图中阴影部分)是( )
A.3π B.π
10.如图,正方形ABCD的边长为 2,连接 BD,先以点 D为圆心,DA 为半径作弧AC,再以点 D 为圆心,DB 为半径作弧 BE,交 DC 延长线于点E,则图中两块阴影部分的面积之和为______________.
11.如图,AB 为⊙O 的直径,将 沿BC 翻折,翻折后的弧交AB于点D.若则图中阴影部分的面积为____________.
参考答案
1. C 2. D 3. D 4. C 5. C
6. C [解析]设阴影部分所在的圆心为O,AD与半圆弧交于点F,如图,连接OF,过点O作于点M.∵AD=在 中,
7. A 8. A 9. A
11.8 [解析]如图,连接AC,CD,过点 C作于点⊥=BC·sin∠ABC=4.∵AB 为⊙O 的直径,∴∠ACB=∴设 根据勾股定理得 ∴m=2 或m=-2(舍去),
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
培优专题 求阴影部分面积的方法
方法一:公式法
温馨提示
如图所示,.
1.如图,菱形OABC的边长为,∠ABC=60°,以O为圆心,对角线OB为半径画弧分别交OA,OC的延长线于点D,E,则扇形DOE的面积为( )
A.π B.2π C.6π D.12π
2.如图,在Rt△ABC中,∠C=90°,CA=CB=4,分别以A,B,C为圆心,以AC为半径画弧,则阴影部分的面积是( )
A.4π B.8-π C.π D.2π
方法二:直接和差法
温馨提示
如图所示:
3.如图,正方形ABCD中,点O为对角线的交点,以点C为圆心,以OC为半径作弧,交BC于点F,交CD于点G,以点D为圆心,以AD为半径作弧,交BD于点E,若AB=2,则阴影部分的面积为( )
A. B. C. D.
4.如图,在边长为8的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是( )
A. B. C. D.
方法三:构造和差法
温馨提示
如图所示:
5.如图,在矩形ABCD中,AB=6,BC=4,以A为圆心,AD长为半径画弧交AB于点E,以C为圆心,CD长为半径画弧交CB的延长线于点F,则图中阴影部分的面积是( )
A.13π B.13π+24 C.13π-24 D.5π+24
6.如图①,有一张矩形纸片 ABCD, 4,上面有一个以AD 为直径的半圆.如图②将纸片沿 DE 折叠,使 A 点落在 BC 上,这时,半圆还露在外面的部分(阴影部分)的面积是( )
方法四:等积转化法
温馨提示
(1)直接等面积转化,如图所示:
注: ∥
(2)平移转化法,如图所示:
注:
(3)对称转化法,如图所示:
注:点D 为 的中点
(4)旋转转化法,如图所示:
注:
注:∠MEN=90°
7.如图,AB 为半圆O的直径,半径( 以OC 为直径的⊙D交AC 于点 E,交BC 于点 F,若 则图中阴影部分的面积为( )
A.2π-2 B.4π-2 C.4π-4 D.π-2
8.如图,正方形ABCD的边长为 4,分别以正方形的三边为直径在正方形内部作半圆,则阴影部分的面积之和是( )
A.8 B.4 C.16π D.4π
9.如图,在矩形ABCD 中,AB=6,BC=3,把以AB 为直径的半圆O绕点 B 顺时针旋转至如图位置(点 A 落在CD上的点 A处),则半圆O扫过的面积(图中阴影部分)是( )
A.3π B.π
10.如图,正方形ABCD的边长为 2,连接 BD,先以点 D为圆心,DA 为半径作弧AC,再以点 D 为圆心,DB 为半径作弧 BE,交 DC 延长线于点E,则图中两块阴影部分的面积之和为______________.
11.如图,AB 为⊙O 的直径,将 沿BC 翻折,翻折后的弧交AB于点D.若则图中阴影部分的面积为____________.
参考答案
1. C 2. D 3. D 4. C 5. C
6. C [解析]设阴影部分所在的圆心为O,AD与半圆弧交于点F,如图,连接OF,过点O作于点M.∵AD=在 中,
7. A 8. A 9. A
11.8 [解析]如图,连接AC,CD,过点 C作于点⊥=BC·sin∠ABC=4.∵AB 为⊙O 的直径,∴∠ACB=∴设 根据勾股定理得 ∴m=2 或m=-2(舍去),
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
