第五章 圆培优专题 分类讨论思想在圆中的应用同步练习(含答案)
文档属性
| 名称 | 第五章 圆培优专题 分类讨论思想在圆中的应用同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 11:47:43 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
培优专题 分类讨论思想在圆中的应用
应用一:点和圆的位置关系不唯一
1.平面内有一点 P,点P 到⊙O 的最远距离是6,最近距离是2,则⊙O 的半径是__________.
应用二:点在直径上的位置不唯一
2.已知⊙O 的直径 AB 是⊙O 的弦,垂 足 为 M,且 则等于( )
或 或
应用三:圆心和平行弦的位置关系不唯一
3.已知⊙O 的半径为5cm,AB 和CD 是⊙O的弦, ∥求AB与CD之间的距离.
应用四:点在圆周上的位置不唯一
4.如图,AB 是⊙O 的弦,若⊙O的半径长为 6,在⊙O 上取一点C,使得 则弦 BC的长度为____________.
5.半径为1的⊙O中,两条弦 的度数为___________.
应用五:三角形的形状不唯一
6.若等腰 内接于⊙O, 则 底角的度数为( )
或 或
应用六:弦所对的圆周角不唯一
7.已知⊙O 的半径为10,弦AB 的长为10,则弦AB 所对的圆周角的度数是_________.
应用七:线段与圆的位置关系不唯一
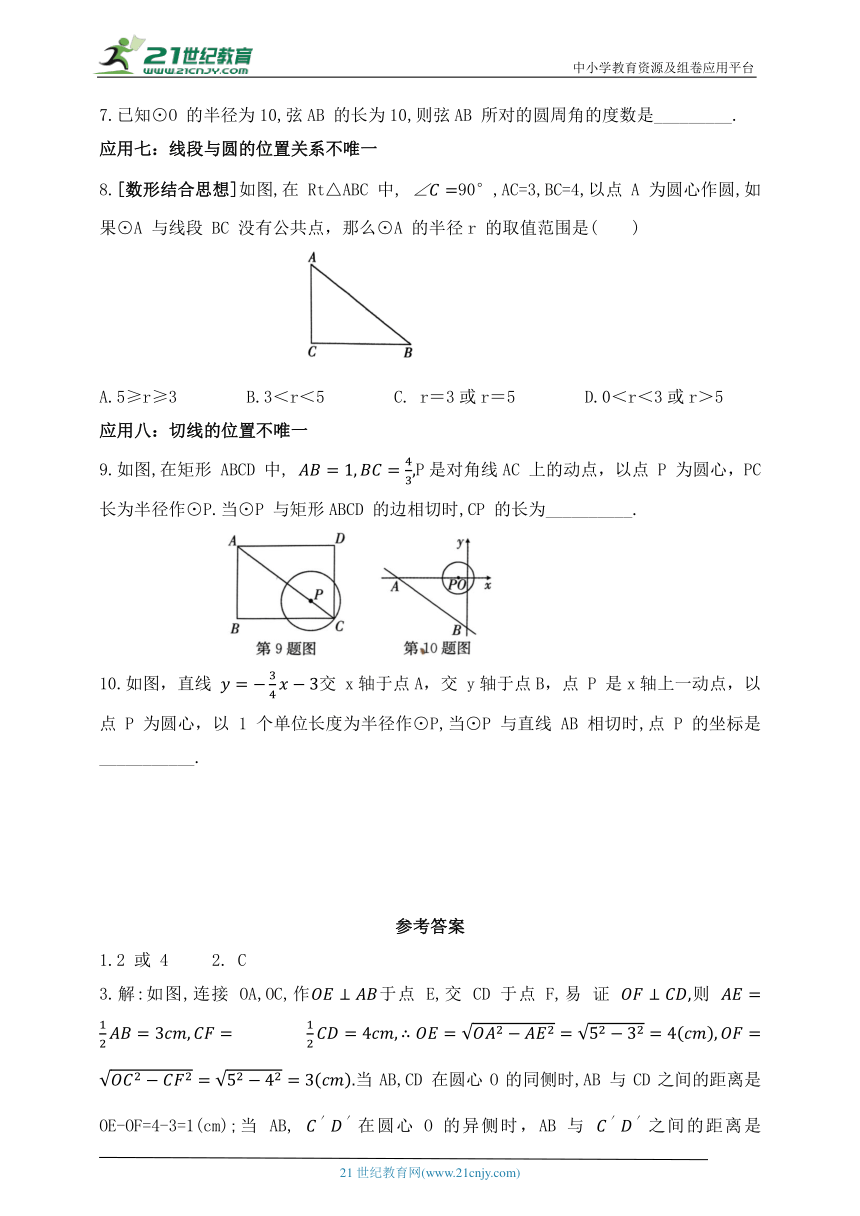
8.[数形结合思想]如图,在 Rt△ABC 中, 90°,AC=3,BC=4,以点A 为圆心作圆,如果⊙A 与线段 BC 没有公共点,那么⊙A 的半径r 的取值范围是( )
A.5≥r≥3 B.3<r<5 C. r=3或r=5 D.0<r<3或r>5
应用八:切线的位置不唯一
9.如图,在矩形 ABCD 中, P是对角线AC 上的动点,以点 P 为圆心,PC
长为半径作⊙P.当⊙P 与矩形ABCD 的边相切时,CP 的长为__________.
10.如图,直线 交 x轴于点A,交 y轴于点B,点 P 是x轴上一动点,以点 P 为圆心,以1个单位长度为半径作⊙P,当⊙P 与直线AB 相切时,点 P 的坐标是___________.
参考答案
1.2 或 4 2. C
3.解:如图,连接 OA,OC,作于点 E,交 CD 于点F,易 证 则 当AB,CD 在圆心O的同侧时,AB 与CD之间的距离是OE-OF=4-3=1(cm);当 AB, 在圆心O的异侧时,AB与 之间的距离是OE+OF'=4+3=7(cm).∴AB 与CD 之间的距离是1cm或7cm.
4.8±2 [解析]如图,连接OA,OB,BC,作BD⊥AC 于点D.由勾股定理的逆定理证出△OAB 是直角三角形,∠AOB=90°,由圆周角定理得出 45°,从而得出△BCD 是等腰直角三角形,则 BD=CD,BC设BD=CD=x,则AD=8 -x.在 Rt△ABD中,根据勾股定理列方程,解方程求出x=4 ±2,即可得出 BC的长度.
5.105°或15° [解析]分类讨论:当AC 与AB 在点A的两旁时,由OA=OC=AC=1,得到△OAC 为等边三角形,则∠OAC=60°,又由 得到△OAB 为等腰直角三角形,则∠OAB=45°,所以∠BAC=45°+60°=105°;当AC与AB 在点A的同旁时,∠BAC=∠OAC-∠OAB=60°-45°=15°.
6. C 7.30°或 150° 8. D
或 [解析]如图,过点 P 作PE⊥AD于点E,PF⊥AB 于点F.在Rt△ABC 中, 由勾股定理得: 由题意可知⊙P只能与矩形ABCD的边AD,AB 相切.当⊙P 与AD 相切时,PE=PC,∵PE⊥AD,CD⊥AD,∴PE∥CD,∴△APE∽△即 解得 当⊙P 与 AB 相切时, 即 解得 综上所述,当⊙P 与矩形ABCD的边相切时,CP 的长为 或
或 [解析]∵直线 交x轴于点A,交 y轴于点B,∴令 ,得y=-3,令. 0,得. , 设⊙P 与直线AB 相切于点 D,连接PD,如图所示,则. 同理可得 ∴点 P 的坐标是 或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
培优专题 分类讨论思想在圆中的应用
应用一:点和圆的位置关系不唯一
1.平面内有一点 P,点P 到⊙O 的最远距离是6,最近距离是2,则⊙O 的半径是__________.
应用二:点在直径上的位置不唯一
2.已知⊙O 的直径 AB 是⊙O 的弦,垂 足 为 M,且 则等于( )
或 或
应用三:圆心和平行弦的位置关系不唯一
3.已知⊙O 的半径为5cm,AB 和CD 是⊙O的弦, ∥求AB与CD之间的距离.
应用四:点在圆周上的位置不唯一
4.如图,AB 是⊙O 的弦,若⊙O的半径长为 6,在⊙O 上取一点C,使得 则弦 BC的长度为____________.
5.半径为1的⊙O中,两条弦 的度数为___________.
应用五:三角形的形状不唯一
6.若等腰 内接于⊙O, 则 底角的度数为( )
或 或
应用六:弦所对的圆周角不唯一
7.已知⊙O 的半径为10,弦AB 的长为10,则弦AB 所对的圆周角的度数是_________.
应用七:线段与圆的位置关系不唯一
8.[数形结合思想]如图,在 Rt△ABC 中, 90°,AC=3,BC=4,以点A 为圆心作圆,如果⊙A 与线段 BC 没有公共点,那么⊙A 的半径r 的取值范围是( )
A.5≥r≥3 B.3<r<5 C. r=3或r=5 D.0<r<3或r>5
应用八:切线的位置不唯一
9.如图,在矩形 ABCD 中, P是对角线AC 上的动点,以点 P 为圆心,PC
长为半径作⊙P.当⊙P 与矩形ABCD 的边相切时,CP 的长为__________.
10.如图,直线 交 x轴于点A,交 y轴于点B,点 P 是x轴上一动点,以点 P 为圆心,以1个单位长度为半径作⊙P,当⊙P 与直线AB 相切时,点 P 的坐标是___________.
参考答案
1.2 或 4 2. C
3.解:如图,连接 OA,OC,作于点 E,交 CD 于点F,易 证 则 当AB,CD 在圆心O的同侧时,AB 与CD之间的距离是OE-OF=4-3=1(cm);当 AB, 在圆心O的异侧时,AB与 之间的距离是OE+OF'=4+3=7(cm).∴AB 与CD 之间的距离是1cm或7cm.
4.8±2 [解析]如图,连接OA,OB,BC,作BD⊥AC 于点D.由勾股定理的逆定理证出△OAB 是直角三角形,∠AOB=90°,由圆周角定理得出 45°,从而得出△BCD 是等腰直角三角形,则 BD=CD,BC设BD=CD=x,则AD=8 -x.在 Rt△ABD中,根据勾股定理列方程,解方程求出x=4 ±2,即可得出 BC的长度.
5.105°或15° [解析]分类讨论:当AC 与AB 在点A的两旁时,由OA=OC=AC=1,得到△OAC 为等边三角形,则∠OAC=60°,又由 得到△OAB 为等腰直角三角形,则∠OAB=45°,所以∠BAC=45°+60°=105°;当AC与AB 在点A的同旁时,∠BAC=∠OAC-∠OAB=60°-45°=15°.
6. C 7.30°或 150° 8. D
或 [解析]如图,过点 P 作PE⊥AD于点E,PF⊥AB 于点F.在Rt△ABC 中, 由勾股定理得: 由题意可知⊙P只能与矩形ABCD的边AD,AB 相切.当⊙P 与AD 相切时,PE=PC,∵PE⊥AD,CD⊥AD,∴PE∥CD,∴△APE∽△即 解得 当⊙P 与 AB 相切时, 即 解得 综上所述,当⊙P 与矩形ABCD的边相切时,CP 的长为 或
或 [解析]∵直线 交x轴于点A,交 y轴于点B,∴令 ,得y=-3,令. 0,得. , 设⊙P 与直线AB 相切于点 D,连接PD,如图所示,则. 同理可得 ∴点 P 的坐标是 或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
