第五章 圆培优专题 圆中的母题与变式同步练习(含答案)
文档属性
| 名称 | 第五章 圆培优专题 圆中的母题与变式同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 11:48:29 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
培优专题 圆中的母题与变式
母题 1 如图,有一块三角尺 ABC, 为直角, 将它放置在⊙O 中,点 A,B在圆上,边 BC 经过圆心O,劣弧 AB 的度数等于____________°.
【思路点拨】连接OA,求出, 即可解决问题.
变式训练 1 如图,将一块三角尺放置在⊙O中,点 A,B在圆上,边 AC 经过圆心O, 为直角, P 为圆上异于A,B的点,则 的度数为( )
或 或
变式训练2 如图,以⊙O 的弦AB 为斜边作C点在圆内,边 BC 经过圆心O,过A 点作⊙O 的切线AD.
(1)求证:
(2)若 求⊙O的半径.
母题2 如图,⊙O 是 的内切圆,切点分别为 D,E,F,已知. 连接 OB,OC,DE,EF,则
【思路点拨】 连接OD和OF,根据内切圆的性质可得 BO,CO分别平分. 再根据三角形内角和定理即可求出. 的度数;根据切线的性质可得 的度数,进而根据圆周角定理可得 的度数.
变式训练3 如图,在 中, I 是内心,O 是外心,则
变式训练4 如图,⊙O是等边 的内切圆,分别切AB,BC,AC 于点E,F,D,P 是
上一点,求 的度数.
母题3 如图,扇形AOB 的圆心角是直角,半径为 C为OB 边上一点,将 沿 AC 边折叠,圆心O恰好落在弧AB 上,则阴影部分面积为( )
D.2π
【思路点拨】 根据题意和折叠的性质,可以得到然后根据 OD,即可得到∠OAC 和∠DAC 的度数,再根据扇形 AOB 的圆心角是直角,半径为 可以得到OC 的长,结合图形,可知阴影部分的面积就是扇形AOB 的面积减. 和 的面积.
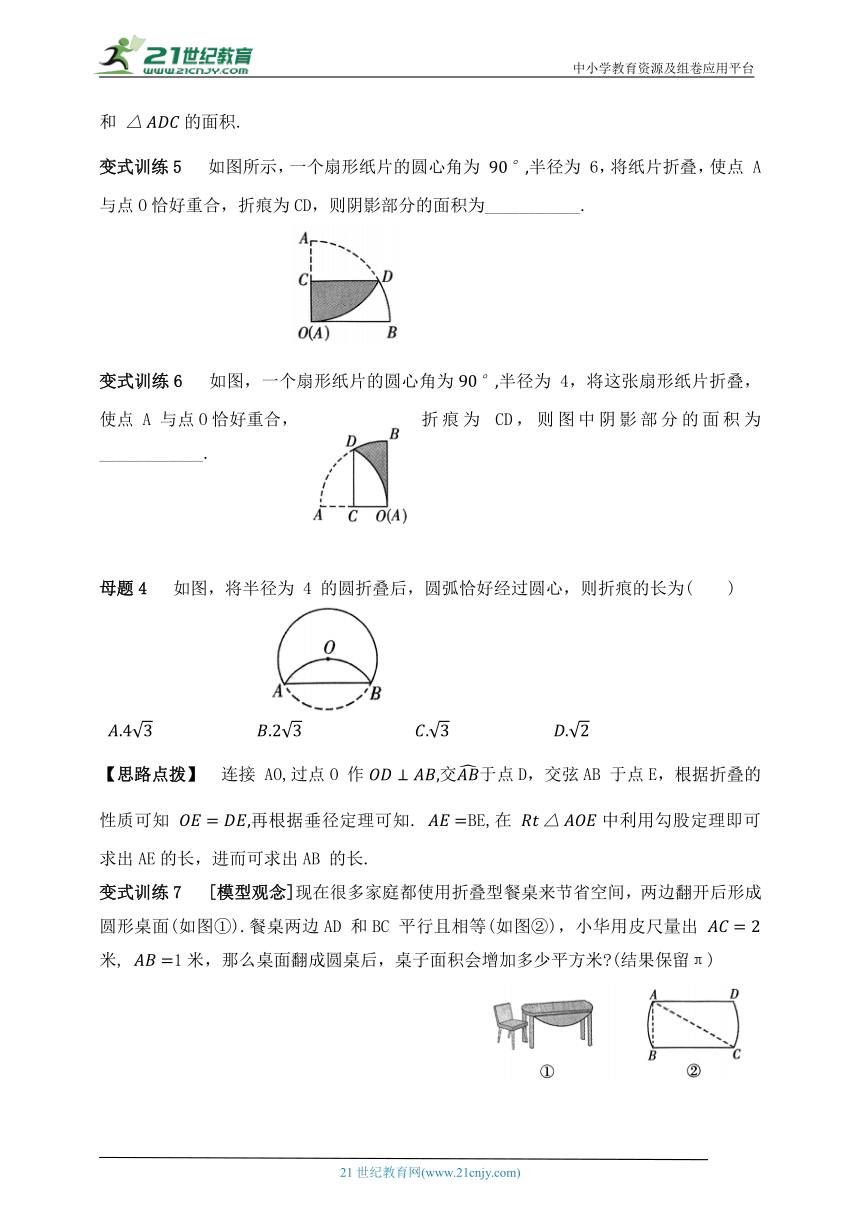
变式训练5 如图所示,一个扇形纸片的圆心角为 半径为 6,将纸片折叠,使点 A 与点O恰好重合,折痕为CD,则阴影部分的面积为___________.
变式训练6 如图,一个扇形纸片的圆心角为半径为 4,将这张扇形纸片折叠,使点 A 与点O恰好重合,折痕为 CD,则图中阴影部分的面积为____________.
母题4 如图,将半径为 4 的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )
【思路点拨】 连接 AO,过点O 作交于点D,交弦AB 于点E,根据折叠的性质可知 再根据垂径定理可知. BE,在 中利用勾股定理即可求出AE的长,进而可求出AB 的长.
变式训练7 [模型观念]现在很多家庭都使用折叠型餐桌来节省空间,两边翻开后形成圆形桌面(如图①).餐桌两边AD 和BC 平行且相等(如图②),小华用皮尺量出 米, 1米,那么桌面翻成圆桌后,桌子面积会增加多少平方米 (结果保留π)
参考答案
母题1:120
变式训练1:D [解析]如图,连接OB,PA,PB.当点 P 在优弧AB 上时, 当点 在劣弧AB 上时, 的度数为 或
变式训练2:(1)证明:连接OA.∵AD 是⊙O的切线,∴OA⊥AD,∴∠OAD=∠CAD+∠OAC=90°.∵∠C=90°,∴∠OAC+∠AOC=90°,∴∠CAD=∠AOC.∵OA=OB,∴∠B=∠OAB,∴∠DAC=∠AOC=∠B +∠OAB=2∠B. (2)解:设 OA=OB=r.在 Rt△CAB 中, 在 Rt△ACO中,由勾股定理得 解得 r= 即⊙O 的半径是 .
母题2:110 70 [解析]连接OD和OF.∵⊙O 是△ABC的内切圆,切点分别为D,E,F,∠A=40°,∴BO,CO分别平分∠ABC,∠ACB,∴∠BOC=180°-∠OBC-∠OCB=⊥AB,OF⊥AC,∴∠ADO=∠AFO=90°,∴∠DOF=360°
变式训练3:140 [解析]∵点I 是△ABC 的内心,∴∠BIC即 ∴ 点 O是△ABC的外心,∴∠BOC=2∠A=2×70°=140°.
变式训练4:解:如图,连接OE,OF.∵⊙O是等边△ABC的内切圆,∴OE⊥AB,OF⊥BC,∴∠BEO=∠BFO=90°,∴∠B+∠EOF=180°.∵△ABC 为等边三角形,∴∠B==60°.
母题3:A [解析]如图,连接OD.∵△AOC沿AC边折叠得到△ADC,∴OA=AD,∠OAC=∠DAC.又∵OA=OD,∴OA=AD=OD,∴△OAD 是等边三角形,∴∠OAC=∠DAC=30°.∵扇形AOB 的圆心角是直角,半径为 ∴OC=2,∴阴影部分的面积.
变式训练5: [解析]如图,连接OD.∵扇形纸片折叠,使点 A 与点O恰好重合,折痕为CD,∴AC=OC,∴OD= D=60°,∴由弧AD、线段AC 和CD所围成的图形的面积=∴阴影部分的面积为
变式训练6: [解析]连接 AD,OD,由折叠可知:S弓形AD=S弓形OD,DA=DO.∵OA=OD,∴AD=OD=OA,∴△AOD 为等边三角形,∴∠AOD=60°,∠DOB=30°.∴阴影部分的面积
母题4:A [解析]如图所示,连接AO,过点O 作OD⊥AB,交 于点D,交弦AB 于点E.∵折叠后恰好经过圆心,∴OE=DE.∵⊙O的半径为4 在 Rt△AOE 中,AE=
变式训练7:解:如图,设圆心为O,连接 DO,过点 O作( AD于点E,易知 米,AB=1米,∴∠ACB=30°.∵餐桌两边 AD 和 BC 平行且相等, 米, 米,米.∵∠1=∠ADO=30°,∴∠AOD=120°,平方米,∴桌面翻成圆桌后,桌子面积会增加 平方米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
培优专题 圆中的母题与变式
母题 1 如图,有一块三角尺 ABC, 为直角, 将它放置在⊙O 中,点 A,B在圆上,边 BC 经过圆心O,劣弧 AB 的度数等于____________°.
【思路点拨】连接OA,求出, 即可解决问题.
变式训练 1 如图,将一块三角尺放置在⊙O中,点 A,B在圆上,边 AC 经过圆心O, 为直角, P 为圆上异于A,B的点,则 的度数为( )
或 或
变式训练2 如图,以⊙O 的弦AB 为斜边作C点在圆内,边 BC 经过圆心O,过A 点作⊙O 的切线AD.
(1)求证:
(2)若 求⊙O的半径.
母题2 如图,⊙O 是 的内切圆,切点分别为 D,E,F,已知. 连接 OB,OC,DE,EF,则
【思路点拨】 连接OD和OF,根据内切圆的性质可得 BO,CO分别平分. 再根据三角形内角和定理即可求出. 的度数;根据切线的性质可得 的度数,进而根据圆周角定理可得 的度数.
变式训练3 如图,在 中, I 是内心,O 是外心,则
变式训练4 如图,⊙O是等边 的内切圆,分别切AB,BC,AC 于点E,F,D,P 是
上一点,求 的度数.
母题3 如图,扇形AOB 的圆心角是直角,半径为 C为OB 边上一点,将 沿 AC 边折叠,圆心O恰好落在弧AB 上,则阴影部分面积为( )
D.2π
【思路点拨】 根据题意和折叠的性质,可以得到然后根据 OD,即可得到∠OAC 和∠DAC 的度数,再根据扇形 AOB 的圆心角是直角,半径为 可以得到OC 的长,结合图形,可知阴影部分的面积就是扇形AOB 的面积减. 和 的面积.
变式训练5 如图所示,一个扇形纸片的圆心角为 半径为 6,将纸片折叠,使点 A 与点O恰好重合,折痕为CD,则阴影部分的面积为___________.
变式训练6 如图,一个扇形纸片的圆心角为半径为 4,将这张扇形纸片折叠,使点 A 与点O恰好重合,折痕为 CD,则图中阴影部分的面积为____________.
母题4 如图,将半径为 4 的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )
【思路点拨】 连接 AO,过点O 作交于点D,交弦AB 于点E,根据折叠的性质可知 再根据垂径定理可知. BE,在 中利用勾股定理即可求出AE的长,进而可求出AB 的长.
变式训练7 [模型观念]现在很多家庭都使用折叠型餐桌来节省空间,两边翻开后形成圆形桌面(如图①).餐桌两边AD 和BC 平行且相等(如图②),小华用皮尺量出 米, 1米,那么桌面翻成圆桌后,桌子面积会增加多少平方米 (结果保留π)
参考答案
母题1:120
变式训练1:D [解析]如图,连接OB,PA,PB.当点 P 在优弧AB 上时, 当点 在劣弧AB 上时, 的度数为 或
变式训练2:(1)证明:连接OA.∵AD 是⊙O的切线,∴OA⊥AD,∴∠OAD=∠CAD+∠OAC=90°.∵∠C=90°,∴∠OAC+∠AOC=90°,∴∠CAD=∠AOC.∵OA=OB,∴∠B=∠OAB,∴∠DAC=∠AOC=∠B +∠OAB=2∠B. (2)解:设 OA=OB=r.在 Rt△CAB 中, 在 Rt△ACO中,由勾股定理得 解得 r= 即⊙O 的半径是 .
母题2:110 70 [解析]连接OD和OF.∵⊙O 是△ABC的内切圆,切点分别为D,E,F,∠A=40°,∴BO,CO分别平分∠ABC,∠ACB,∴∠BOC=180°-∠OBC-∠OCB=⊥AB,OF⊥AC,∴∠ADO=∠AFO=90°,∴∠DOF=360°
变式训练3:140 [解析]∵点I 是△ABC 的内心,∴∠BIC即 ∴ 点 O是△ABC的外心,∴∠BOC=2∠A=2×70°=140°.
变式训练4:解:如图,连接OE,OF.∵⊙O是等边△ABC的内切圆,∴OE⊥AB,OF⊥BC,∴∠BEO=∠BFO=90°,∴∠B+∠EOF=180°.∵△ABC 为等边三角形,∴∠B==60°.
母题3:A [解析]如图,连接OD.∵△AOC沿AC边折叠得到△ADC,∴OA=AD,∠OAC=∠DAC.又∵OA=OD,∴OA=AD=OD,∴△OAD 是等边三角形,∴∠OAC=∠DAC=30°.∵扇形AOB 的圆心角是直角,半径为 ∴OC=2,∴阴影部分的面积.
变式训练5: [解析]如图,连接OD.∵扇形纸片折叠,使点 A 与点O恰好重合,折痕为CD,∴AC=OC,∴OD= D=60°,∴由弧AD、线段AC 和CD所围成的图形的面积=∴阴影部分的面积为
变式训练6: [解析]连接 AD,OD,由折叠可知:S弓形AD=S弓形OD,DA=DO.∵OA=OD,∴AD=OD=OA,∴△AOD 为等边三角形,∴∠AOD=60°,∠DOB=30°.∴阴影部分的面积
母题4:A [解析]如图所示,连接AO,过点O 作OD⊥AB,交 于点D,交弦AB 于点E.∵折叠后恰好经过圆心,∴OE=DE.∵⊙O的半径为4 在 Rt△AOE 中,AE=
变式训练7:解:如图,设圆心为O,连接 DO,过点 O作( AD于点E,易知 米,AB=1米,∴∠ACB=30°.∵餐桌两边 AD 和 BC 平行且相等, 米, 米,米.∵∠1=∠ADO=30°,∴∠AOD=120°,平方米,∴桌面翻成圆桌后,桌子面积会增加 平方米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
