11.2直线的倾斜角和斜率1

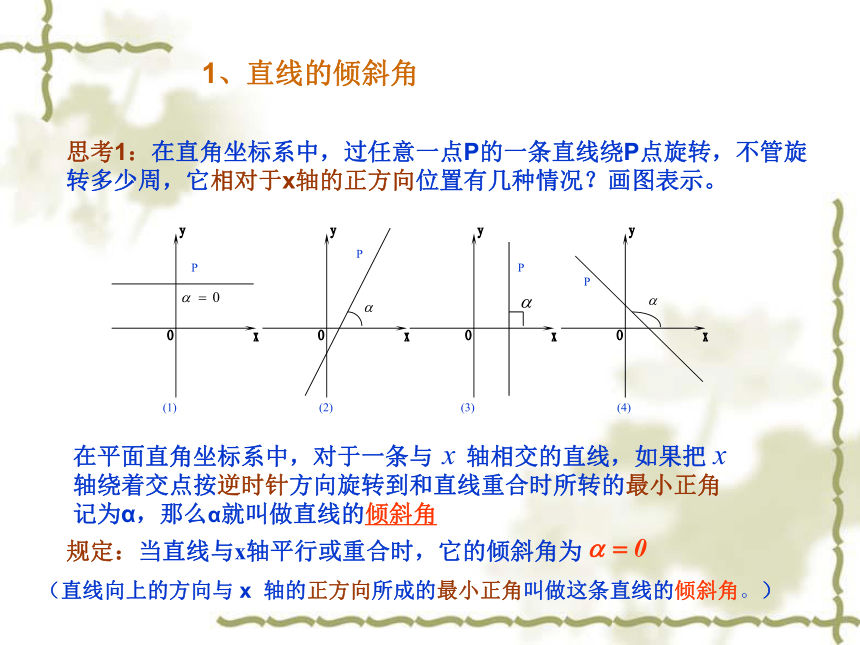
课件13张PPT。倾斜角和斜率（１）11.2直线的1、直线的倾斜角思考1：在直角坐标系中，过任意一点P的一条直线绕P点旋转，不管旋转多少周，它相对于x轴的正方向位置有几种情况？画图表示。（直线向上的方向与 x 轴的正方向所成的最小正角叫做这条直线的倾斜角。）在平面直角坐标系中，对于一条与 轴相交的直线，如果把 轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记为α，那么α就叫做直线的倾斜角 规定：当直线与x轴平行或重合时，它的倾斜角为 思考2：下列图中标出的直线的倾斜角 对不对？如果不对，违背了定义中的哪一条？在平面直角坐标系中，对于一条与 轴相交的直线，如果把 轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记为 ，那么 就叫做直线的倾斜角 思考3：直线的倾斜角能不能是 ？能不能是锐角？能不能是直角？能不能是钝角？能不能是平角？能否大于平角？直线倾斜角的范围是： ，在此范围内，坐标平面上的任何一条直线都有唯一的倾斜角，而每一个倾斜角都能确定一条直线的方向。倾斜角直观的表示了直线相对于x轴正方向的倾斜程度。 2、直线的斜率思考4：当 时， k 值如何？当 时，k 值如何？
当 时， k值如何？当 时， k 值如何？思考5： 1. 下列说法中正确的是 （ ）倾斜角不是 的直线，它的倾斜角的正切叫做这条直线的斜率。
用 表示，即 ：C2. 直线 经过点（ ）和（ ），其中 则（ ）B 3.直线的方向向量（u，v）、倾斜角α与斜率k的关系 当u=0时，直线垂直x轴，k不存在，当u≠0时， 也是一个方向向量，而k
存在，再由上面的分析知（1，k）也是方向向量， 故 （这个结论也可以从几何角度研究得到）； 如果已知α ，那么k=tan α ， =(cos α,sin α)；如果已知k,那么α可以由tan α =k求得， 　＝（1，k） 。 　4．过两点的直线的斜率公式： 是直线 上的两点，则当 时，
是直线 的一个方向向量， 过两点 的直线的斜率 ；
当 时，直线斜率不存在。倾斜角和斜率（2）11.2直线的1、直线的倾斜角在平面直角坐标系中，对于一条与x轴相交的直线，如果把x 轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记为α，那么α就叫做直线的倾斜角。 规定：当直线与x轴平行或重合时，它的
倾斜角为 复习直线倾斜角的范围是： ，在此范围内，坐标平面上的任何一条直线都有唯一的倾斜角，而每一个倾斜角都能确定一条直线的方向。倾斜角直观的表示了直线相对于x轴正方向的倾斜程度。 2、直线的斜率倾斜角不是 的直线，它的倾斜角的
正切叫做这条直线的斜率。
用k表示，即：k=tan α当 时，k值不存在。
3.直线的方向向量（u，v）、倾斜角α与斜 率k的关系 当u=0时，直线垂直x轴，k不存在，当u≠0时， 也是一个方向向量，而k
存在，再由上面的分析知（1，k）也是方向向量， 故 （这个结论也可以从几何角度研究得到）； 如果已知α ，那么k=tan α ， =(cos α,sin α)；如果已知k,那么α可以由tan α =k求得， 　＝（1，k） 。 　4．过两点的直线的斜率公式： 是直线 上的两点，则当 时，
是直线 的一个方向向量， 过两点 的直线的斜率 ；
当 时，直线斜率不存在。新课：直线的一般式方程的定义 直线的点方向式方程和直线的点法向式方程经过整理，成为关于x、y的二元一次方程ax+by+c=0。二元一次方程ax+by+c=0（a、b不全为0）是直线的方程，叫做直线的一般式方程。 直线的一个法向量是 ，一个方向向量是 （-b，a）