11.2.1直线的倾斜角和斜率

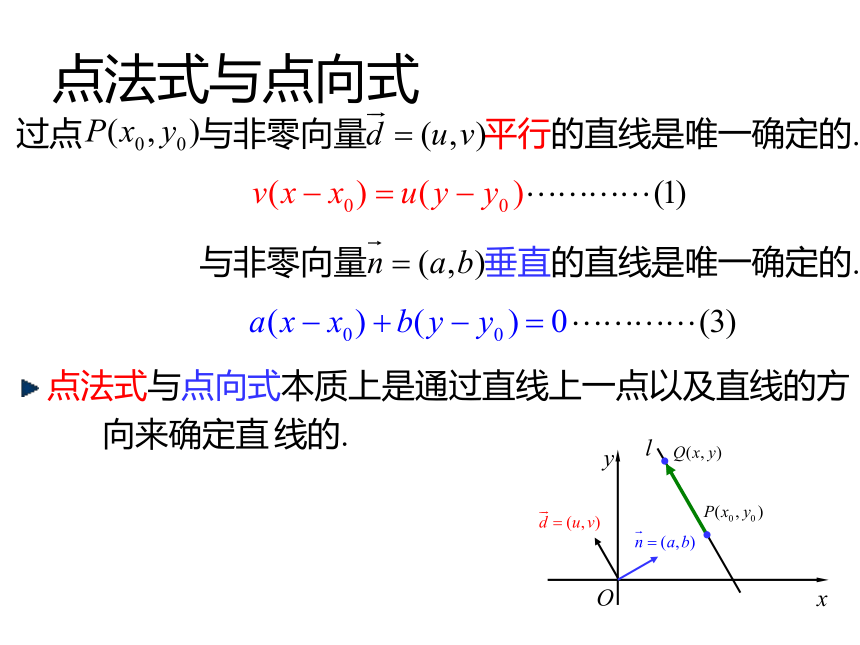
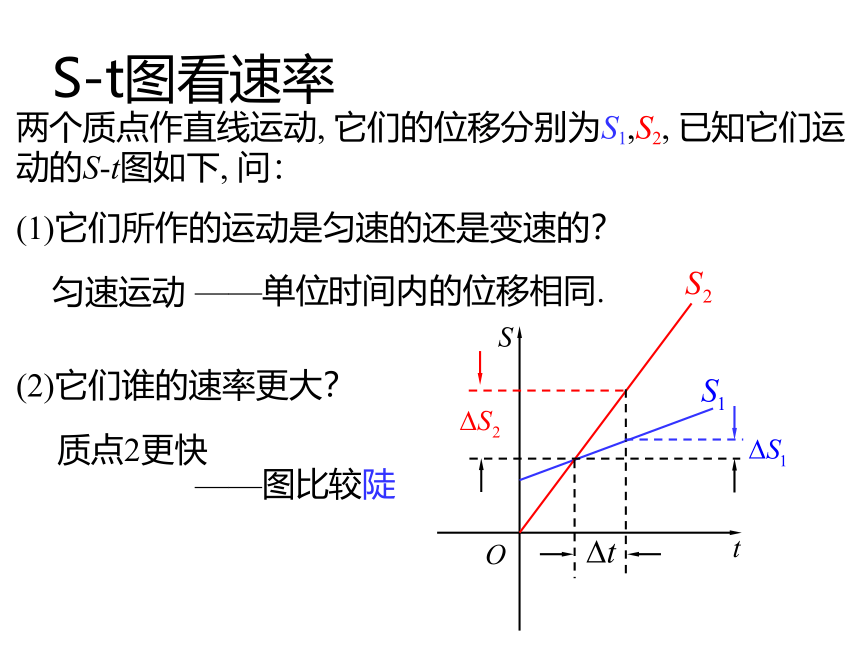
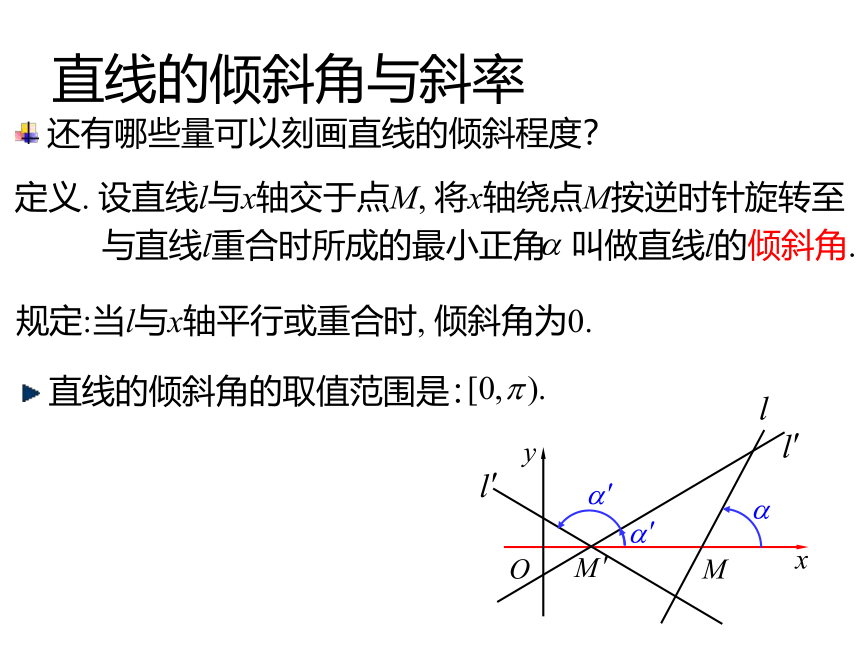
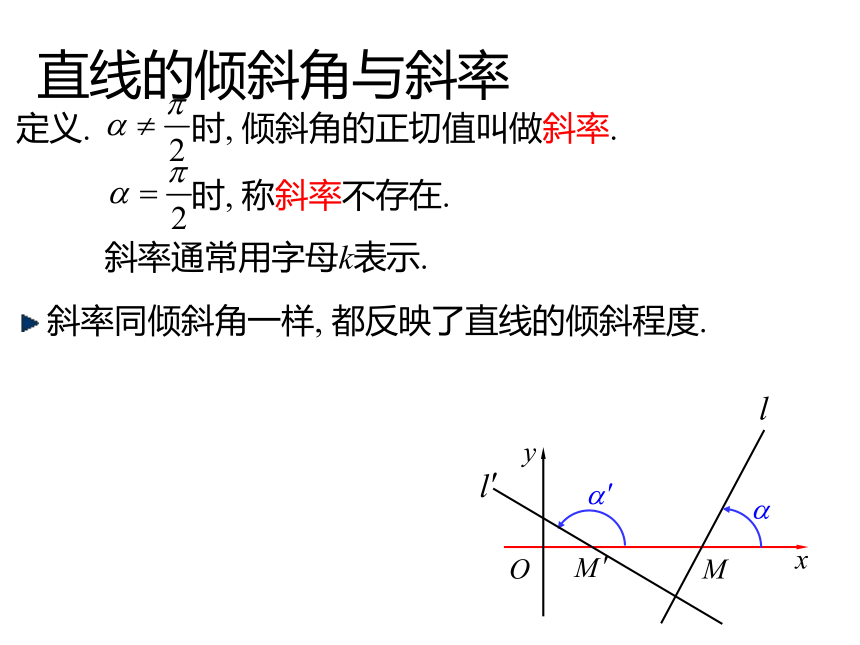
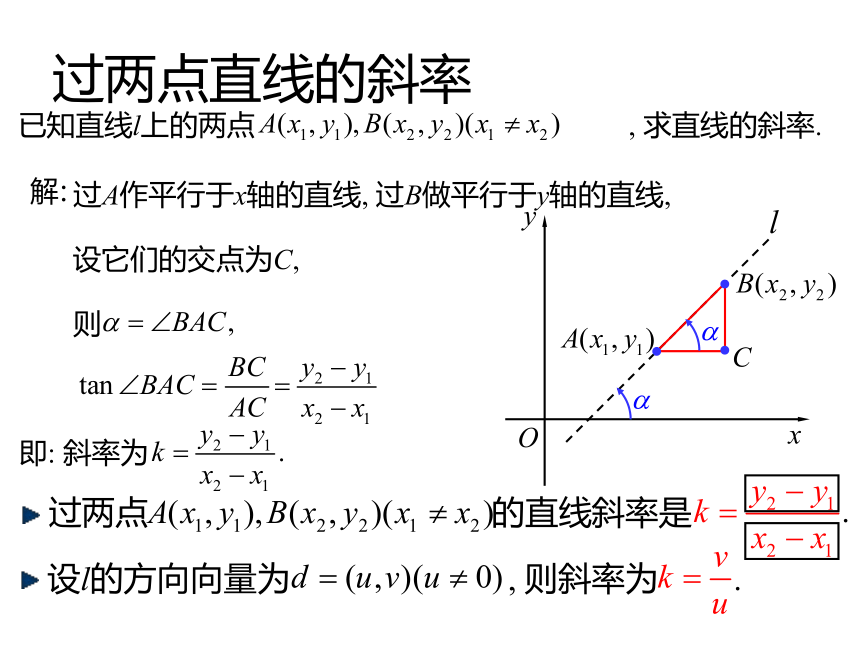
课件14张PPT。【第11章 坐标平面上的直线】直线的倾斜角和斜率点法式与点向式 与非零向量 垂直的直线是唯一确定的.过点 与非零向量 平行的直线是唯一确定的. 点法式与点向式本质上是通过直线上一点以及直线的方 向来确定直 线的.S-t图看速率两个质点作直线运动, 它们的位移分别为S1,S2, 已知它们运动的S-t图如下, 问：(1)它们所作的运动是匀速的还是变速的？(2)它们谁的速率更大？OtS匀速运动——单位时间内的位移相同.质点2更快——图比较陡规定:当l与x轴平行或重合时, 倾斜角为0.直线的倾斜角与斜率Oxy 还有哪些量可以刻画直线的倾斜程度？M定义. 设直线l与x轴交于点M, 将x轴绕点M按逆时针旋转至 与直线l重合时所成的最小正角 叫做直线l的倾斜角. 直线的倾斜角的取值范围是：OxyM定义. 时, 倾斜角的正切值叫做斜率. 时, 称斜率不存在.斜率通常用字母k表示. 斜率同倾斜角一样, 都反映了直线的倾斜程度.直线的倾斜角与斜率过两点直线的斜率已知直线l上的两点 , 求直线的斜率.Oxy解:过A作平行于x轴的直线, 过B做平行于y轴的直线,设它们的交点为C,则即: 斜率为 过两点 的直线斜率是 设l的方向向量为 , 则斜率为 .推导 思考, 过点 倾斜角为 的直线唯一么？为什么？yxO唯一.若不唯一, 设有另一条l?符合条件,由同位角相等, 两直线平行, 与平行线公理矛盾！故而： 过点 倾斜角为 的直线是唯一的！求过点 倾斜角为 , 斜率为 的直线.yxO设 在直线l上,则由过两点的直线的斜率公式：直线上的点的坐标都满足方程.以方程的解为坐标的点都在直线上.推导且不同于P.特别地, 是方程的解.点斜式方程过点 倾斜角为 , 斜率为 的直线为：yxO称方程(5)为直线的点斜式方程. 方程(5)所确定的直线的方向向量和法向量是什么？ 是(4)的一个法向量. 是(4)的一个方向向量.点斜式的局限性过点 倾斜角为 , 斜率为 的直线为：称方程(5)为直线的点斜式方程. 直线的点斜式方程是否具有局限性？由 可知, 点斜式无法表示垂直于x轴的直线.由点斜式中要求yxO例1.已知直线l过点(1)求直线的斜率k及倾角;(2)求直线的方程;(3)将l绕A顺时针旋转 , 求所得直线l?的方程.【典型例题】一般化:过两点 直线的点斜式方程.Oxy解:由过两点的直线的斜率公式：代入点斜式方程, 得：称方程(7)为直线的两点式方程.若再有 ,则点斜式方程例2.求直线 的斜率及倾斜角的大小.例3.求直线 的斜率及倾斜角的大小.解:斜率不存在, 但倾斜角是 .【典型例题】解:课内小结定义. 设直线l与x轴交于点M, 将x轴绕点M按逆时针旋转至 与直线l重合时所成的最小正角 叫做直线l的倾斜角.定义. 时, 倾斜角的正切值叫做斜率. 时, 称斜率不存在.过点 倾斜角为 , 斜率为 的直线为：称方程(5)为直线的点斜式方程.由 可知, 点斜式无法表示垂直于x轴的直线.