人教版数学九年级上册 22.2 二次函数与一元二次方程 学案(无答案)
文档属性
| 名称 | 人教版数学九年级上册 22.2 二次函数与一元二次方程 学案(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 112.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 00:00:00 | ||
图片预览

文档简介
二次函数与一元二次方程
班级: 姓名: 组号:
【课时安排】
2课时
第一课时
一、旧知回顾
1.一次函数与轴的交点坐标为 ,与轴的交点坐标为 。
2.画出函数的图象,从图象直接观察写出:当取何值时,;当取何值时,?
【新知探究】
3.认真阅读问题及分析过程,完成下列各题:
(1)结合已知条件和图形,写出你可以获得的信息(至少写出4个);
(2)你对分析和解答过程是否理解,请把不明白的问题写出来。
(3)请对课本中的两个云图的问题进行解释。
认真阅读P44“从上面可以看出,……”内容,理解二次函数与一元二次方程关于从数的角度的关系:
从形的角度看,二次函数的值为,求自变量的值,可以看作在图象上纵坐标为的点的横坐标。也就是图象上纵坐标为的点的横坐标就是一元二次方程的解。
4.认真阅读课本P44“思考”-P45“归纳”的内容完成下列各题:
(1)一元二次方程就是二次函数图象上纵坐标为的点的横坐标,因此一元二次方程的解就是二次函数与 轴交点的横坐标。
(2)归纳一元二次方程的解和抛物线与轴交点个数的关系?
5.认真阅读课本P46内容体会如何用图象求一元二次方程的近似解。
试一试
6.画出函数的图象,观察图象,当x取哪些值时,函数值为0?
7.用函数的图象求方程的解。
★通过预习你还有什么困惑
课堂活动、记录
1.一元二次方程与二次函数有什么系?
2.二次函数的图象与轴交点的个数与一元二次方程根的情况有什么关系?
3.如何用图象求一元二次方程的解?
【精练反馈】
1.二次函数y=x2-3x+2,当x=1时,y=________;当y=0时,x=_______ 。
2.二次函数y=x2-4x+6,当x=________时,y=3.
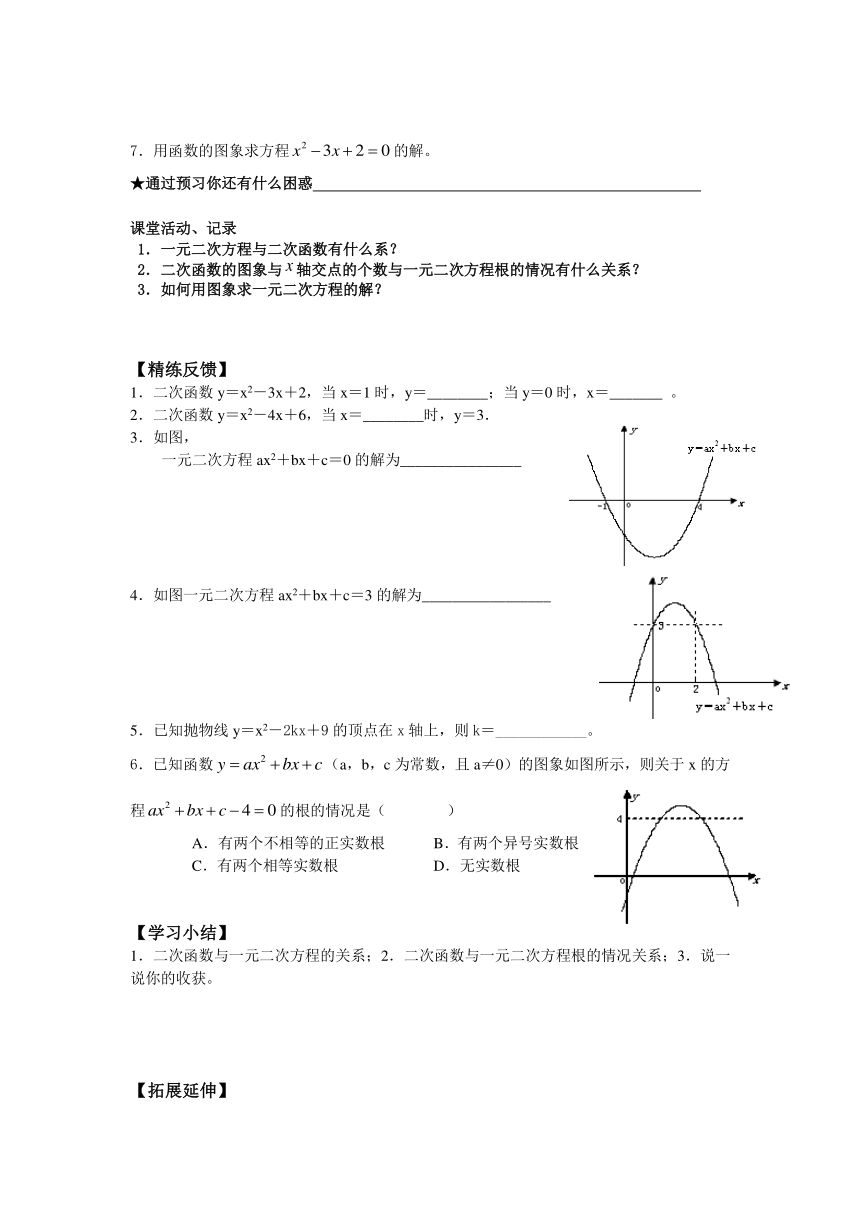
3.如图,
一元二次方程ax2+bx+c=0的解为________________
4.如图一元二次方程ax2+bx+c=3的解为_________________
5.已知抛物线y=x2-2kx+9的顶点在x轴上,则k=____________。
6.已知函数(a,b,c为常数,且a≠0)的图象如图所示,则关于x的方程的根的情况是( )
A.有两个不相等的正实数根 B.有两个异号实数根
C.有两个相等实数根 D.无实数根
【学习小结】
1.二次函数与一元二次方程的关系;2.二次函数与一元二次方程根的情况关系;3.说一说你的收获。
【拓展延伸】
1.下列情形时,如果a>0,抛物线的顶点在什么位置?
(1)方程有两个不等的实数根;
(2)方程有两个相等的实数根;(3)方程无实数根。如果a<0呢?
2.利用抛物线图象求解一元二次方程及二次不等式
(1)方程ax2+bx+c=0的根为___________;
(2)方程ax2+bx+c=-3的根为__________;
(3)方程ax2+bx+c=-4的根为__________;
(4)不等式ax2+bx+c>0的解集为________;
(5)不等式ax2+bx+c<0的解集为________;
( (6)不等式-4<ax2+bx+c<0的解集为________。
第二课时
拓展课
一、巩固训练
1.抛物线y=x2+2x-3与x轴的交点有______个。
2. 如果二次函数(a>0)的顶点在x轴上方,那么 ( )
A、B2-4ac≥0 B.b2-4ac<0 C.b2-4ac>0 D.b2-4ac=0
3. 已知二次函数的图象如图所示,则关于的方程 的根的情况是 ( )
A。有两个不相等的正实数根 B.有两个异号实数根
C.有两个相等的实数根 D.没有实数根
二、错题再现
1.二次函数y=a x+bx+c(a≠0)的图象如图,下列结论正确的是( )
A.a<0 B.b2-4ac<0 C.当-10 D.-=1
2.已知抛物线y=x2+x+c与x轴没有交点。
(1)求c的取值范围;
(2)试确定直线y=cx+1经过的象限,并说明理由。
三、能力提升
“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根。”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系( )
A.m<a<b<n B.a<m<n<b C.a<m<b<n D.m<a<n<b
四、精练反馈
A组:
1.已知二次函数的图象和x轴有交点,则k的取值范围是 ( )
A. k> B. k≥ C. k≥且k≠0 D. k>且k≠0
B组:
2.如图22 2 7,将二次函数y=31x2-999x+892的图形画在平面直角坐标系上,判断方程式31x2-999x+892=0的两根,下列叙述正确的是( )
A.两根相异,且均为正根 B.两根相异,且只有一个正根
C.两根相同,且为正根 D.两根相同,且为负根
3.已知二次函数的部分图象如图所示,抛物线与轴的一个交点坐标为,对称轴为直线,若实数,比较与的大小,并说明理由。
班级: 姓名: 组号:
【课时安排】
2课时
第一课时
一、旧知回顾
1.一次函数与轴的交点坐标为 ,与轴的交点坐标为 。
2.画出函数的图象,从图象直接观察写出:当取何值时,;当取何值时,?
【新知探究】
3.认真阅读问题及分析过程,完成下列各题:
(1)结合已知条件和图形,写出你可以获得的信息(至少写出4个);
(2)你对分析和解答过程是否理解,请把不明白的问题写出来。
(3)请对课本中的两个云图的问题进行解释。
认真阅读P44“从上面可以看出,……”内容,理解二次函数与一元二次方程关于从数的角度的关系:
从形的角度看,二次函数的值为,求自变量的值,可以看作在图象上纵坐标为的点的横坐标。也就是图象上纵坐标为的点的横坐标就是一元二次方程的解。
4.认真阅读课本P44“思考”-P45“归纳”的内容完成下列各题:
(1)一元二次方程就是二次函数图象上纵坐标为的点的横坐标,因此一元二次方程的解就是二次函数与 轴交点的横坐标。
(2)归纳一元二次方程的解和抛物线与轴交点个数的关系?
5.认真阅读课本P46内容体会如何用图象求一元二次方程的近似解。
试一试
6.画出函数的图象,观察图象,当x取哪些值时,函数值为0?
7.用函数的图象求方程的解。
★通过预习你还有什么困惑
课堂活动、记录
1.一元二次方程与二次函数有什么系?
2.二次函数的图象与轴交点的个数与一元二次方程根的情况有什么关系?
3.如何用图象求一元二次方程的解?
【精练反馈】
1.二次函数y=x2-3x+2,当x=1时,y=________;当y=0时,x=_______ 。
2.二次函数y=x2-4x+6,当x=________时,y=3.
3.如图,
一元二次方程ax2+bx+c=0的解为________________
4.如图一元二次方程ax2+bx+c=3的解为_________________
5.已知抛物线y=x2-2kx+9的顶点在x轴上,则k=____________。
6.已知函数(a,b,c为常数,且a≠0)的图象如图所示,则关于x的方程的根的情况是( )
A.有两个不相等的正实数根 B.有两个异号实数根
C.有两个相等实数根 D.无实数根
【学习小结】
1.二次函数与一元二次方程的关系;2.二次函数与一元二次方程根的情况关系;3.说一说你的收获。
【拓展延伸】
1.下列情形时,如果a>0,抛物线的顶点在什么位置?
(1)方程有两个不等的实数根;
(2)方程有两个相等的实数根;(3)方程无实数根。如果a<0呢?
2.利用抛物线图象求解一元二次方程及二次不等式
(1)方程ax2+bx+c=0的根为___________;
(2)方程ax2+bx+c=-3的根为__________;
(3)方程ax2+bx+c=-4的根为__________;
(4)不等式ax2+bx+c>0的解集为________;
(5)不等式ax2+bx+c<0的解集为________;
( (6)不等式-4<ax2+bx+c<0的解集为________。
第二课时
拓展课
一、巩固训练
1.抛物线y=x2+2x-3与x轴的交点有______个。
2. 如果二次函数(a>0)的顶点在x轴上方,那么 ( )
A、B2-4ac≥0 B.b2-4ac<0 C.b2-4ac>0 D.b2-4ac=0
3. 已知二次函数的图象如图所示,则关于的方程 的根的情况是 ( )
A。有两个不相等的正实数根 B.有两个异号实数根
C.有两个相等的实数根 D.没有实数根
二、错题再现
1.二次函数y=a x+bx+c(a≠0)的图象如图,下列结论正确的是( )
A.a<0 B.b2-4ac<0 C.当-1
2.已知抛物线y=x2+x+c与x轴没有交点。
(1)求c的取值范围;
(2)试确定直线y=cx+1经过的象限,并说明理由。
三、能力提升
“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根。”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系( )
A.m<a<b<n B.a<m<n<b C.a<m<b<n D.m<a<n<b
四、精练反馈
A组:
1.已知二次函数的图象和x轴有交点,则k的取值范围是 ( )
A. k> B. k≥ C. k≥且k≠0 D. k>且k≠0
B组:
2.如图22 2 7,将二次函数y=31x2-999x+892的图形画在平面直角坐标系上,判断方程式31x2-999x+892=0的两根,下列叙述正确的是( )
A.两根相异,且均为正根 B.两根相异,且只有一个正根
C.两根相同,且为正根 D.两根相同,且为负根
3.已知二次函数的部分图象如图所示,抛物线与轴的一个交点坐标为,对称轴为直线,若实数,比较与的大小,并说明理由。
同课章节目录
