第五章 圆章末复习题(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章 圆
章末复习
考点整合
考点一:垂径定理
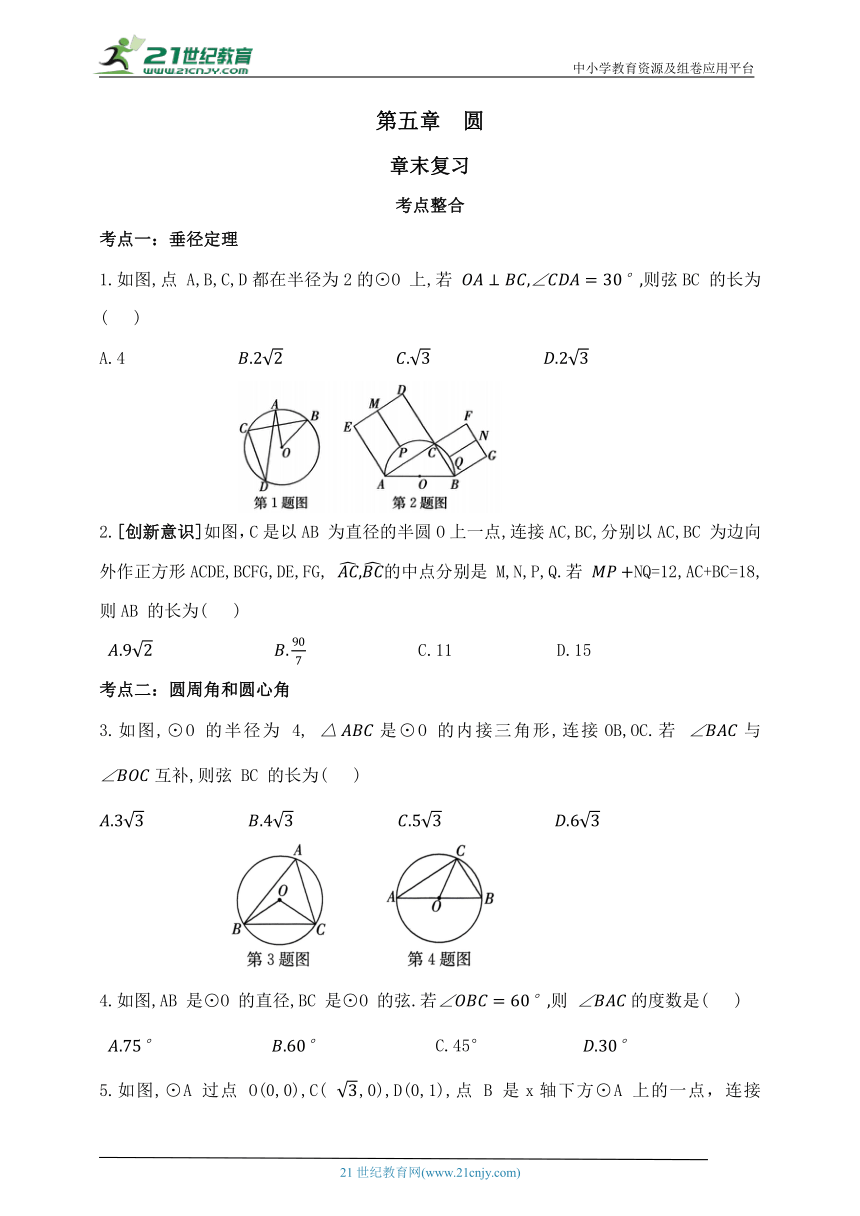
1.如图,点 A,B,C,D都在半径为2的⊙O 上,若 则弦BC 的长为( )
A.4
2.[创新意识]如图,C是以AB 为直径的半圆O上一点,连接AC,BC,分别以AC,BC 为边向外作正方形ACDE,BCFG,DE,FG, 的中点分别是 M,N,P,Q.若 NQ=12,AC+BC=18,则AB 的长为( )
C.11 D.15
考点二:圆周角和圆心角
3.如图,⊙O 的半径为 4, 是⊙O 的内接三角形,连接OB,OC.若 与 互补,则弦 BC 的长为( )
4.如图,AB 是⊙O 的直径,BC 是⊙O 的弦.若则 的度数是( )
C.45°
5.如图,⊙A 过点 O(0,0),C( ,0),D(0,1),点 B 是x轴下方⊙A 上的一点,连接 BO,BD,则 的度数是( )
6.如图,已知AC 是⊙O 的直径,点 B 在圆周上(不与点 A,C 重合),点 D 在AC 的延长线上,连接 BD 交⊙O 于点 E,若 则( )
7.如图,⊙P 与x轴交于点. B(1,0),与 y 轴的 正 半 轴 交 于 点 C. 若则点 C 的纵坐标为( )
8.如图,在 中,以BC为直径作半圆O,交AB 于点D,交 AC 于点E,
(1)求证:
(2)若 求 AD 的长.
考点三:直线和圆的位置关系
9.如图,AB 为⊙O 的切线,点 A为切点,OB 交⊙O 于点C,点 D 在⊙O 上,连接AD,CD,OA,若 则 的度数为( )
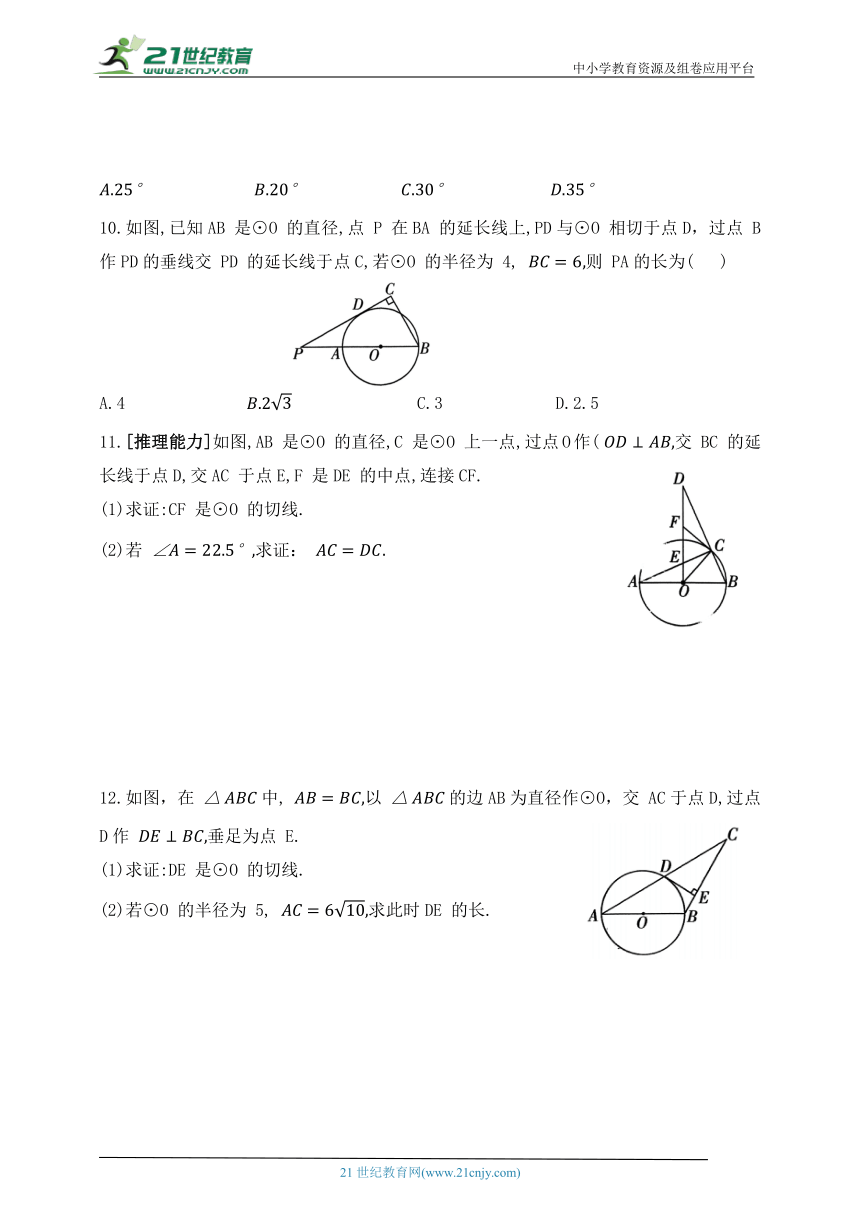
10.如图,已知AB 是⊙O 的直径,点 P 在BA 的延长线上,PD与⊙O 相切于点D,过点 B 作PD的垂线交 PD 的延长线于点C,若⊙O 的半径为 4, 则 PA的长为( )
A.4 C.3 D.2.5
11.[推理能力]如图,AB 是⊙O 的直径,C 是⊙O 上一点,过点O作( 交 BC 的延长线于点D,交AC 于点E,F 是DE 的中点,连接CF.
(1)求证:CF 是⊙O 的切线.
(2)若 求证:
12.如图,在 中, 以 的边AB为直径作⊙O,交 AC于点D,过点 D作 垂足为点 E.
(1)求证:DE 是⊙O 的切线.
(2)若⊙O 的半径为 5, 求此时DE 的长.
考点四:弧长、扇形的面积与圆锥的侧面展开图
13.制造弯形管道时,经常要先按中心线计算“展直长度”,再下料.如图是一段弯形管道,其中 中心线的两条弧的半径都是1000 mm,这段弯形管道的展直长度约为(π取3.14)( )
A.9280 mm B.6280 mm C.6140 mm D.457 mm
14.如图,在⊙O 中, ,则阴影部分的面积是( )
15.如图,有一块半径为1m 的半圆形铁皮,要把它做成一个圆锥形容器的侧面(接缝忽略不计),那么这个圆锥形容器的高为( )
16.如图,在 中, 的平分线AD交 BC于 点D,点E 在AC上,以AE为直径的⊙O 经过点D.
(1)①求证:BC 是⊙O 的切线.
②求证:
(2)若点 F 是劣弧AD 的中点,且试求阴影部分的面积.
数学思想
思想一:分类讨论思想
1.已知⊙O 的半径为 10 cm,AB,CD 是⊙O 的两条弦, 则弦 AB 和 CD 之间的距离是__________cm.
2.如图,⊙O 的半径( B 是⊙O 上的动点(不与点 A 重合),过点 B 作⊙O 的切线BC,BC=OA,连接OC,AC.当 是直角三角形时,其斜边长为_____________.
思想二:方程思想
3.如图,以的直角边AB为直径作⊙O 交斜边 AC 于点 D,过圆心O作 ∥交BC 于点E,连接DE.
(1)判断 DE 与⊙O 的位置关系并说明理由.
(2)求证:
(3)若 求 AD的长.
参考答案
考点整合
1. D
2. D [解析]如图,连接OP,OQ,分别交 AC,BC 于点 H,I.的中点分别是 M,N,P,Q, AC,OQ⊥BC,∴H,I 是 AC,BD 的中点,
3. B 4. D 5. B 6. D
7. B [解析]连接PA,PB,PC,过点P作 于点D,PE⊥OC 于点E.根据圆周角定理得到. 根据等腰三角形的性质得到 由垂径定理得到AD=BD=3,解直角三角形得到 PA易得 PE=DO=2,根据勾股定理得到进一步可求出点 C的纵坐标.
8.(1)证明:连接BE,CD.∵BC 是半圆O的直径,∴∠BDC=∠BEC=90°,∴∠ADC=∠AEB=90°.∵在△ABE 和△ACD中,∠AEB =∠ADC,AE=AD,∠A =∠A,∴△ABE≌△ACD,∴AB=AC. (2)解: 在 Rt△BDC中, 设AD=x,则AC=AB=x+4,在Rt△ADC 中, 解得x=6,即AD=6.
9. B 10. A
11.证明:(1)∵AB 是⊙O的直径,∴∠ACB=∠ACD=90°.∵点F 是ED的中点,∴CF=EF=DF,∴∠AEO=∠FEC=∠FCE. ∵OA =OC,∴∠OCA =∠OAC.∵OD⊥AB,∴∠OAC+∠AEO =90°,∴∠OCA +∠FCE=90°,即OC⊥FC,∴CF 是⊙O 的切线.
(2)连接AD.∵OD⊥AB,AC⊥BD,∴∠AOE=∠ACD=90°.∵∠AEO=∠DEC,∴∠OAE=∠CDE=22.5°.∠ADC=45°,∴AC=DC.
12.(1)证明:连接OD,BD.∵AB 是⊙O 的直径,∴∠ADB=90°,∴BD⊥AC.∵AB=BC,∴D为 AC 中点.∵OA=OB,∴OD∥BC.∵DE⊥BC,∴DE⊥OD.∵OD 为半径,∴DE 是⊙O的切线. (2)解:由(1)知 D 是 AC 的中点, )的半径为 5,.∵AB=BC,∴∠A=∠C.∵∠ADB=∠CED=即 ∴DE=3.
13. C
14. A [解析]连接OA,OB,OC.∵AB=AC,∴AB=AC.
∵∠ACB=75°,∴∠ABC=∠ACB=75°,∴∠BAC=30°,∴∠BOC=60°.∵OB=OC,∴△BOC 是等边三角形,∴OA=OB=OC=BC=2.作AD⊥BC 交 BC 于点D.∵AB=AC,∴BD=CD,∴AD 经过圆心O,∴BD=
15. D
16.(1)证明:①连接 OD.∵AD 是∠BAC 的平分线,∴∠DAB=∠DAO.∵OD=OA,∴∠DAO=∠ODA,∴∠DAB=∠ADO,∴DO∥AB,而∠B=90°,∴∠ODB=90°,∴BC 是⊙O 的切线. ②连接 DE.∵BC 是⊙O的切线,∴易证∠CDE =∠DAC. 又∵∠C=∠C,
(2)解:连接 DF,OF,设圆的半径为 R.∵点 F 是劣弧AD 的中点,∴OF 是 DA 的中垂线,∴DF =AF,∴∠FDA=∠FAD.∵DO∥AB,∴∠ODA=∠DAF,∴∠ADO=∠DAO=∠FDA=∠FAD,∴AF=DF=OA = OD, ∴△OFD,△OFA 是 等边三角形,而 OE=
数学思想
1.2 或 14
2.2 或 [解析]连接OB.∵BC是 ⊙O的切线,∴∠OBC=90°.∵BC=OA,∴OB=BC=2,∴△OBC 是等腰直角三角形,∴∠BCO=45°,∴∠ACO≤45°.当△OAC是直角三角形时,分以下情况讨论:
①如图①,∠AOC = 90°. 易 得 .
②如图②,∠OAC=90°.∵BC 是⊙O 的切线,∴∠CBO=∠OAC=90°.∵BC=OA=OB,∴△OBC 是等腰直角三角形,. 故答案为 或
3.(1)解:DE 与⊙O 相切.理由:连接OD,BD.∵AB 是⊙O的直径,∴∠ADB=∠BDC=90°.∵OE∥AC,OA=OB,∵点D在⊙O 上,∴DE 与⊙O 相切.
(2)证明: 由(1)知 由(1)知,OE 是的中位线, (3)解: 在中, 设 根据勾股定理,得 (舍去)或. 1 由(2)知,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
章末复习
考点整合
考点一:垂径定理
1.如图,点 A,B,C,D都在半径为2的⊙O 上,若 则弦BC 的长为( )
A.4
2.[创新意识]如图,C是以AB 为直径的半圆O上一点,连接AC,BC,分别以AC,BC 为边向外作正方形ACDE,BCFG,DE,FG, 的中点分别是 M,N,P,Q.若 NQ=12,AC+BC=18,则AB 的长为( )
C.11 D.15
考点二:圆周角和圆心角
3.如图,⊙O 的半径为 4, 是⊙O 的内接三角形,连接OB,OC.若 与 互补,则弦 BC 的长为( )
4.如图,AB 是⊙O 的直径,BC 是⊙O 的弦.若则 的度数是( )
C.45°
5.如图,⊙A 过点 O(0,0),C( ,0),D(0,1),点 B 是x轴下方⊙A 上的一点,连接 BO,BD,则 的度数是( )
6.如图,已知AC 是⊙O 的直径,点 B 在圆周上(不与点 A,C 重合),点 D 在AC 的延长线上,连接 BD 交⊙O 于点 E,若 则( )
7.如图,⊙P 与x轴交于点. B(1,0),与 y 轴的 正 半 轴 交 于 点 C. 若则点 C 的纵坐标为( )
8.如图,在 中,以BC为直径作半圆O,交AB 于点D,交 AC 于点E,
(1)求证:
(2)若 求 AD 的长.
考点三:直线和圆的位置关系
9.如图,AB 为⊙O 的切线,点 A为切点,OB 交⊙O 于点C,点 D 在⊙O 上,连接AD,CD,OA,若 则 的度数为( )
10.如图,已知AB 是⊙O 的直径,点 P 在BA 的延长线上,PD与⊙O 相切于点D,过点 B 作PD的垂线交 PD 的延长线于点C,若⊙O 的半径为 4, 则 PA的长为( )
A.4 C.3 D.2.5
11.[推理能力]如图,AB 是⊙O 的直径,C 是⊙O 上一点,过点O作( 交 BC 的延长线于点D,交AC 于点E,F 是DE 的中点,连接CF.
(1)求证:CF 是⊙O 的切线.
(2)若 求证:
12.如图,在 中, 以 的边AB为直径作⊙O,交 AC于点D,过点 D作 垂足为点 E.
(1)求证:DE 是⊙O 的切线.
(2)若⊙O 的半径为 5, 求此时DE 的长.
考点四:弧长、扇形的面积与圆锥的侧面展开图
13.制造弯形管道时,经常要先按中心线计算“展直长度”,再下料.如图是一段弯形管道,其中 中心线的两条弧的半径都是1000 mm,这段弯形管道的展直长度约为(π取3.14)( )
A.9280 mm B.6280 mm C.6140 mm D.457 mm
14.如图,在⊙O 中, ,则阴影部分的面积是( )
15.如图,有一块半径为1m 的半圆形铁皮,要把它做成一个圆锥形容器的侧面(接缝忽略不计),那么这个圆锥形容器的高为( )
16.如图,在 中, 的平分线AD交 BC于 点D,点E 在AC上,以AE为直径的⊙O 经过点D.
(1)①求证:BC 是⊙O 的切线.
②求证:
(2)若点 F 是劣弧AD 的中点,且试求阴影部分的面积.
数学思想
思想一:分类讨论思想
1.已知⊙O 的半径为 10 cm,AB,CD 是⊙O 的两条弦, 则弦 AB 和 CD 之间的距离是__________cm.
2.如图,⊙O 的半径( B 是⊙O 上的动点(不与点 A 重合),过点 B 作⊙O 的切线BC,BC=OA,连接OC,AC.当 是直角三角形时,其斜边长为_____________.
思想二:方程思想
3.如图,以的直角边AB为直径作⊙O 交斜边 AC 于点 D,过圆心O作 ∥交BC 于点E,连接DE.
(1)判断 DE 与⊙O 的位置关系并说明理由.
(2)求证:
(3)若 求 AD的长.
参考答案
考点整合
1. D
2. D [解析]如图,连接OP,OQ,分别交 AC,BC 于点 H,I.的中点分别是 M,N,P,Q, AC,OQ⊥BC,∴H,I 是 AC,BD 的中点,
3. B 4. D 5. B 6. D
7. B [解析]连接PA,PB,PC,过点P作 于点D,PE⊥OC 于点E.根据圆周角定理得到. 根据等腰三角形的性质得到 由垂径定理得到AD=BD=3,解直角三角形得到 PA易得 PE=DO=2,根据勾股定理得到进一步可求出点 C的纵坐标.
8.(1)证明:连接BE,CD.∵BC 是半圆O的直径,∴∠BDC=∠BEC=90°,∴∠ADC=∠AEB=90°.∵在△ABE 和△ACD中,∠AEB =∠ADC,AE=AD,∠A =∠A,∴△ABE≌△ACD,∴AB=AC. (2)解: 在 Rt△BDC中, 设AD=x,则AC=AB=x+4,在Rt△ADC 中, 解得x=6,即AD=6.
9. B 10. A
11.证明:(1)∵AB 是⊙O的直径,∴∠ACB=∠ACD=90°.∵点F 是ED的中点,∴CF=EF=DF,∴∠AEO=∠FEC=∠FCE. ∵OA =OC,∴∠OCA =∠OAC.∵OD⊥AB,∴∠OAC+∠AEO =90°,∴∠OCA +∠FCE=90°,即OC⊥FC,∴CF 是⊙O 的切线.
(2)连接AD.∵OD⊥AB,AC⊥BD,∴∠AOE=∠ACD=90°.∵∠AEO=∠DEC,∴∠OAE=∠CDE=22.5°.∠ADC=45°,∴AC=DC.
12.(1)证明:连接OD,BD.∵AB 是⊙O 的直径,∴∠ADB=90°,∴BD⊥AC.∵AB=BC,∴D为 AC 中点.∵OA=OB,∴OD∥BC.∵DE⊥BC,∴DE⊥OD.∵OD 为半径,∴DE 是⊙O的切线. (2)解:由(1)知 D 是 AC 的中点, )的半径为 5,.∵AB=BC,∴∠A=∠C.∵∠ADB=∠CED=即 ∴DE=3.
13. C
14. A [解析]连接OA,OB,OC.∵AB=AC,∴AB=AC.
∵∠ACB=75°,∴∠ABC=∠ACB=75°,∴∠BAC=30°,∴∠BOC=60°.∵OB=OC,∴△BOC 是等边三角形,∴OA=OB=OC=BC=2.作AD⊥BC 交 BC 于点D.∵AB=AC,∴BD=CD,∴AD 经过圆心O,∴BD=
15. D
16.(1)证明:①连接 OD.∵AD 是∠BAC 的平分线,∴∠DAB=∠DAO.∵OD=OA,∴∠DAO=∠ODA,∴∠DAB=∠ADO,∴DO∥AB,而∠B=90°,∴∠ODB=90°,∴BC 是⊙O 的切线. ②连接 DE.∵BC 是⊙O的切线,∴易证∠CDE =∠DAC. 又∵∠C=∠C,
(2)解:连接 DF,OF,设圆的半径为 R.∵点 F 是劣弧AD 的中点,∴OF 是 DA 的中垂线,∴DF =AF,∴∠FDA=∠FAD.∵DO∥AB,∴∠ODA=∠DAF,∴∠ADO=∠DAO=∠FDA=∠FAD,∴AF=DF=OA = OD, ∴△OFD,△OFA 是 等边三角形,而 OE=
数学思想
1.2 或 14
2.2 或 [解析]连接OB.∵BC是 ⊙O的切线,∴∠OBC=90°.∵BC=OA,∴OB=BC=2,∴△OBC 是等腰直角三角形,∴∠BCO=45°,∴∠ACO≤45°.当△OAC是直角三角形时,分以下情况讨论:
①如图①,∠AOC = 90°. 易 得 .
②如图②,∠OAC=90°.∵BC 是⊙O 的切线,∴∠CBO=∠OAC=90°.∵BC=OA=OB,∴△OBC 是等腰直角三角形,. 故答案为 或
3.(1)解:DE 与⊙O 相切.理由:连接OD,BD.∵AB 是⊙O的直径,∴∠ADB=∠BDC=90°.∵OE∥AC,OA=OB,∵点D在⊙O 上,∴DE 与⊙O 相切.
(2)证明: 由(1)知 由(1)知,OE 是的中位线, (3)解: 在中, 设 根据勾股定理,得 (舍去)或. 1 由(2)知,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
