第五章 圆培优专题 圆中常用结论与模型同步练习(含答案)
文档属性
| 名称 | 第五章 圆培优专题 圆中常用结论与模型同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 11:49:26 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
培优专题 圆中常用结论与模型
温馨提示
本专题中归纳的模型及其结论可以在选择题或填空题中直接使用!
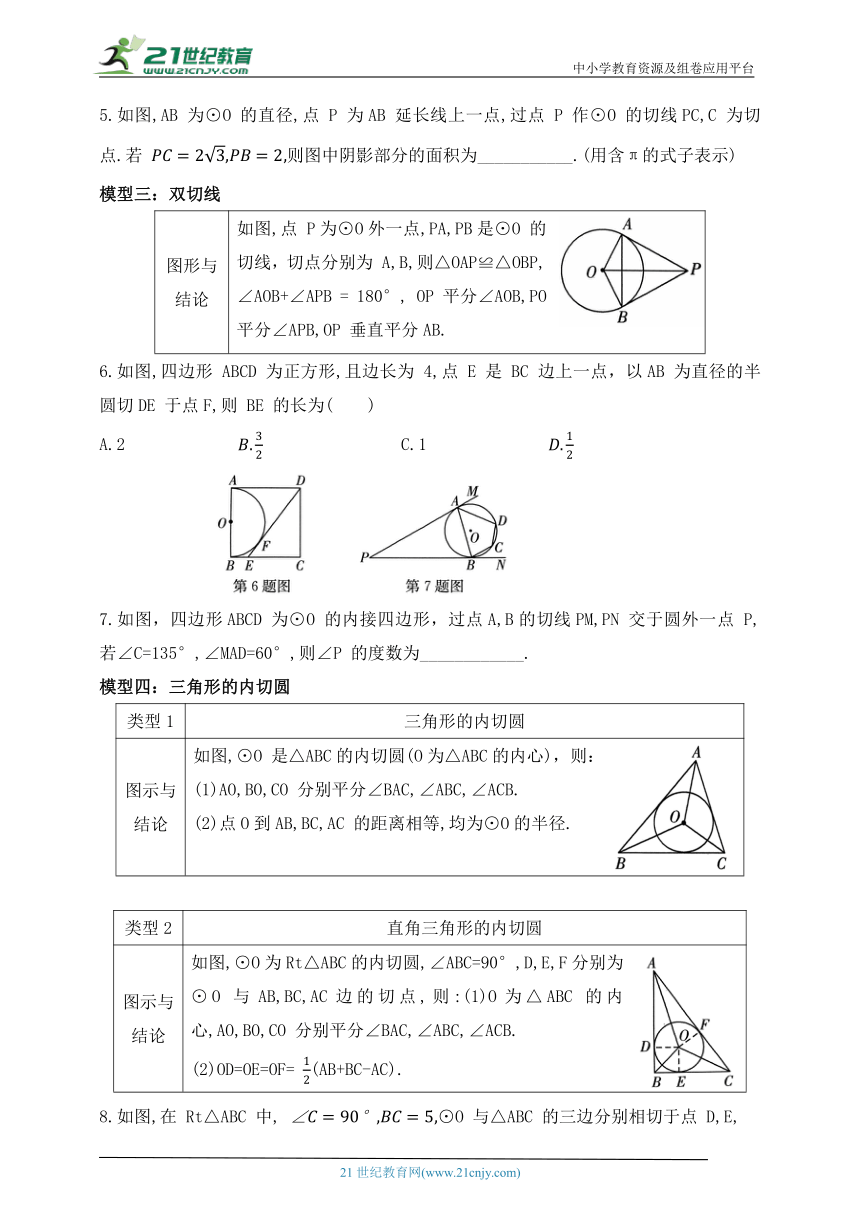
模型一:相交弦定理
图示与结论 如图,⊙O 内任意弦AB与弦CD相交于点E,则EA·EB=EC·ED.
证明 证明:如图,连接 AC,BD.∵∠AEC=∠DEB,∠A=∠D,∴△AEC∽△DEB,.∴,∴EA·EB=EC·ED.
1.如图,⊙O 的直径CD 垂直弦AB 于点 E,且CE=3,DE=7,则AE=( )
A.4 B.2
2.如图,在⊙O中,弦AB⊥弦CD 于点E,连接AD,BC,若 则弦AB 的长为( )
A.4 D.5
3.如图,△ABC 内接于一圆中,AB 是直径,点 D 是BC的中点,连接 AD 交BC 于 点 E,若 CE = 1, 则线段 BD的长为______________.
模型二:切割线定理
类型1切割线定理
图示与 结论 如图,在⊙O 中,弦AB 的延长线交⊙O的切线CD于点D,则CD =BD·AD.
证明 证明:如图,连接 AC,BC.∵∠BCD 是⊙O的弦切角,∴∠BCD=∠A.∵∠D=∠D,∴△ACD∽△CBD,∴,∴CD =BD·AD.
类型2 割线定理
图示与 结论 如图,在⊙O中,弦AB 与弦 CD 的延长线交于点E,点 E在⊙O 外,则 EB·EA=ED·EC.
证明 证明:方法一:如图①,连接 AD,BC.∠E=∠E,∠A=∠C,∴△AED∽△CEB,∴,∴EB·EA=ED·EC. 方法二:如图②,连接 BD,AC. ∵A,B,C,D 是⊙O 上的四个点,∴∠C+ ∠ABD = 180°.∵∠ABD+∠DBE=180°,∴∠C=∠DBE.∵∠E=∠E,∴△EBD∽ △ECA,∴,∴EB·EA=ED·EC.
4.如图,AB 为⊙O 的直径,C,D分别为AB 两侧⊙O 上的点,连接CB 并延长交AD的延长线于点E,连接AC.若 B为CE 的中点,则AD 的长为( )
5.如图,AB 为⊙O 的直径,点 P 为AB 延长线上一点,过点 P 作⊙O 的切线PC,C 为切点.若 则图中阴影部分的面积为___________.(用含π的式子表示)
模型三:双切线
图形与 结论 如图,点 P为⊙O外一点,PA,PB是⊙O 的切线,切点分别为 A,B,则△OAP≌△OBP, ∠AOB+∠APB = 180°, OP 平分∠AOB,PO平分∠APB,OP 垂直平分AB.
6.如图,四边形 ABCD 为正方形,且边长为 4,点 E 是 BC 边上一点,以AB 为直径的半圆切DE 于点F,则 BE 的长为( )
A.2 C.1
7.如图,四边形ABCD 为⊙O 的内接四边形,过点A,B的切线PM,PN 交于圆外一点 P,若∠C=135°,∠MAD=60°,则∠P 的度数为____________.
模型四:三角形的内切圆
类型1 三角形的内切圆
图示与 结论 如图,⊙O 是△ABC的内切圆(O为△ABC的内心),则:(1)AO,BO,CO 分别平分∠BAC,∠ABC,∠ACB. (2)点O到AB,BC,AC 的距离相等,均为⊙O的半径.
类型2 直角三角形的内切圆
图示与 结论 如图,⊙O为Rt△ABC的内切圆,∠ABC=90°,D,E,F分别为⊙O 与AB,BC,AC边的切点,则:(1)O为△ABC 的内心,AO,BO,CO 分别平分∠BAC,∠ABC,∠ACB. (2)OD=OE=OF= (AB+BC-AC).
8.如图,在 Rt△ABC 中, ⊙O 与△ABC 的三边分别相切于点 D,E,
F,若⊙O 的半径为 2,则△ABC 的周长为_____________.
9.如图,点 M 是 的内心, 5,BC=3,将 平移使点C 与点 M 重合,平移后的AC,BC 分别交AB于点 D,E,则 的值为____________.
模型五:定点定长——翻折生圆
图示与 结论 如图,在矩形 ABCD 中,点 E 是AB 边上的定点,点 F 是 BC 边上一点,将△BEF 沿 EF 折叠得到△B′EF,则点B′的运动轨迹是以点E为圆心,BE长为半径的一段圆弧(如图中的虚线圆弧)
10.如图,在四边形 ABCD中, 则 的度数为_________.
11.在边长为 6 的正方形ABCD中,点 E 为CD边上靠近点C 的三等分点,点 F 为 BC 上一动点,将 沿EF折叠,点C 的对应点为 连接 求 的最小值.
12.[模型观念]如图,在矩形ABCD中, 点 E 是 BC 边上的动点(不与 B,C
重合),连接 DE,作点 C 关于 DE 的对称点求 的最小值.
参考答案
1. C 2. B 3. 4. B 6. C 7.30° 8.30
[解析]连接MA ,MB,先确定 的周长,再确定与 的周长比,进而确定面积比.
11.解:如图,以点 E 为圆心,EC 长为半径作圆,连接 BE 交⊙E 于点 P,则 即 的最小值为BE 的长.∵正方形 ABCD的边长为 6,点 E 为CD边靠近点C 的三等分点, 即 的最小值为
12.解:如图,以点 D 为圆心,DC 长为半径作圆,连接 BD 交⊙D 于点 即为最小值,∵四边形 ABCD 是矩形,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
培优专题 圆中常用结论与模型
温馨提示
本专题中归纳的模型及其结论可以在选择题或填空题中直接使用!
模型一:相交弦定理
图示与结论 如图,⊙O 内任意弦AB与弦CD相交于点E,则EA·EB=EC·ED.
证明 证明:如图,连接 AC,BD.∵∠AEC=∠DEB,∠A=∠D,∴△AEC∽△DEB,.∴,∴EA·EB=EC·ED.
1.如图,⊙O 的直径CD 垂直弦AB 于点 E,且CE=3,DE=7,则AE=( )
A.4 B.2
2.如图,在⊙O中,弦AB⊥弦CD 于点E,连接AD,BC,若 则弦AB 的长为( )
A.4 D.5
3.如图,△ABC 内接于一圆中,AB 是直径,点 D 是BC的中点,连接 AD 交BC 于 点 E,若 CE = 1, 则线段 BD的长为______________.
模型二:切割线定理
类型1切割线定理
图示与 结论 如图,在⊙O 中,弦AB 的延长线交⊙O的切线CD于点D,则CD =BD·AD.
证明 证明:如图,连接 AC,BC.∵∠BCD 是⊙O的弦切角,∴∠BCD=∠A.∵∠D=∠D,∴△ACD∽△CBD,∴,∴CD =BD·AD.
类型2 割线定理
图示与 结论 如图,在⊙O中,弦AB 与弦 CD 的延长线交于点E,点 E在⊙O 外,则 EB·EA=ED·EC.
证明 证明:方法一:如图①,连接 AD,BC.∠E=∠E,∠A=∠C,∴△AED∽△CEB,∴,∴EB·EA=ED·EC. 方法二:如图②,连接 BD,AC. ∵A,B,C,D 是⊙O 上的四个点,∴∠C+ ∠ABD = 180°.∵∠ABD+∠DBE=180°,∴∠C=∠DBE.∵∠E=∠E,∴△EBD∽ △ECA,∴,∴EB·EA=ED·EC.
4.如图,AB 为⊙O 的直径,C,D分别为AB 两侧⊙O 上的点,连接CB 并延长交AD的延长线于点E,连接AC.若 B为CE 的中点,则AD 的长为( )
5.如图,AB 为⊙O 的直径,点 P 为AB 延长线上一点,过点 P 作⊙O 的切线PC,C 为切点.若 则图中阴影部分的面积为___________.(用含π的式子表示)
模型三:双切线
图形与 结论 如图,点 P为⊙O外一点,PA,PB是⊙O 的切线,切点分别为 A,B,则△OAP≌△OBP, ∠AOB+∠APB = 180°, OP 平分∠AOB,PO平分∠APB,OP 垂直平分AB.
6.如图,四边形 ABCD 为正方形,且边长为 4,点 E 是 BC 边上一点,以AB 为直径的半圆切DE 于点F,则 BE 的长为( )
A.2 C.1
7.如图,四边形ABCD 为⊙O 的内接四边形,过点A,B的切线PM,PN 交于圆外一点 P,若∠C=135°,∠MAD=60°,则∠P 的度数为____________.
模型四:三角形的内切圆
类型1 三角形的内切圆
图示与 结论 如图,⊙O 是△ABC的内切圆(O为△ABC的内心),则:(1)AO,BO,CO 分别平分∠BAC,∠ABC,∠ACB. (2)点O到AB,BC,AC 的距离相等,均为⊙O的半径.
类型2 直角三角形的内切圆
图示与 结论 如图,⊙O为Rt△ABC的内切圆,∠ABC=90°,D,E,F分别为⊙O 与AB,BC,AC边的切点,则:(1)O为△ABC 的内心,AO,BO,CO 分别平分∠BAC,∠ABC,∠ACB. (2)OD=OE=OF= (AB+BC-AC).
8.如图,在 Rt△ABC 中, ⊙O 与△ABC 的三边分别相切于点 D,E,
F,若⊙O 的半径为 2,则△ABC 的周长为_____________.
9.如图,点 M 是 的内心, 5,BC=3,将 平移使点C 与点 M 重合,平移后的AC,BC 分别交AB于点 D,E,则 的值为____________.
模型五:定点定长——翻折生圆
图示与 结论 如图,在矩形 ABCD 中,点 E 是AB 边上的定点,点 F 是 BC 边上一点,将△BEF 沿 EF 折叠得到△B′EF,则点B′的运动轨迹是以点E为圆心,BE长为半径的一段圆弧(如图中的虚线圆弧)
10.如图,在四边形 ABCD中, 则 的度数为_________.
11.在边长为 6 的正方形ABCD中,点 E 为CD边上靠近点C 的三等分点,点 F 为 BC 上一动点,将 沿EF折叠,点C 的对应点为 连接 求 的最小值.
12.[模型观念]如图,在矩形ABCD中, 点 E 是 BC 边上的动点(不与 B,C
重合),连接 DE,作点 C 关于 DE 的对称点求 的最小值.
参考答案
1. C 2. B 3. 4. B 6. C 7.30° 8.30
[解析]连接MA ,MB,先确定 的周长,再确定与 的周长比,进而确定面积比.
11.解:如图,以点 E 为圆心,EC 长为半径作圆,连接 BE 交⊙E 于点 P,则 即 的最小值为BE 的长.∵正方形 ABCD的边长为 6,点 E 为CD边靠近点C 的三等分点, 即 的最小值为
12.解:如图,以点 D 为圆心,DC 长为半径作圆,连接 BD 交⊙D 于点 即为最小值,∵四边形 ABCD 是矩形,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
