第五章 圆综合练习题(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
第五章 圆
综合练习
一、选择题
1.如图,点A,B,C,D均在直线上,点 P 在直线外,则经过其中任意三个点,最多可画出圆的个数为( )
A.3 B.4 C.5 D.6
2.如图,⊙O 是 的外接圆,若 则
A.25°
3.如图,正五边形 ABCDE 内接于⊙O,连接 OC,OD,则. ( )
A.60° B.54° C.48° D.36°
4.如图所示,等边△ABC 的顶点A在⊙O 上,边 AB,AC 与⊙O分别交于点D,E,点 F 是劣弧 DE 上一点,且与D,E 不重合,连接 DF,EF,则 的度数为( )
A.115° B.118° C.120°
5.如图,AB切⊙O 于点B,连接OA交⊙O 于点C, ∥交⊙O 于 点D,连接CD,若 则 的度数为( )
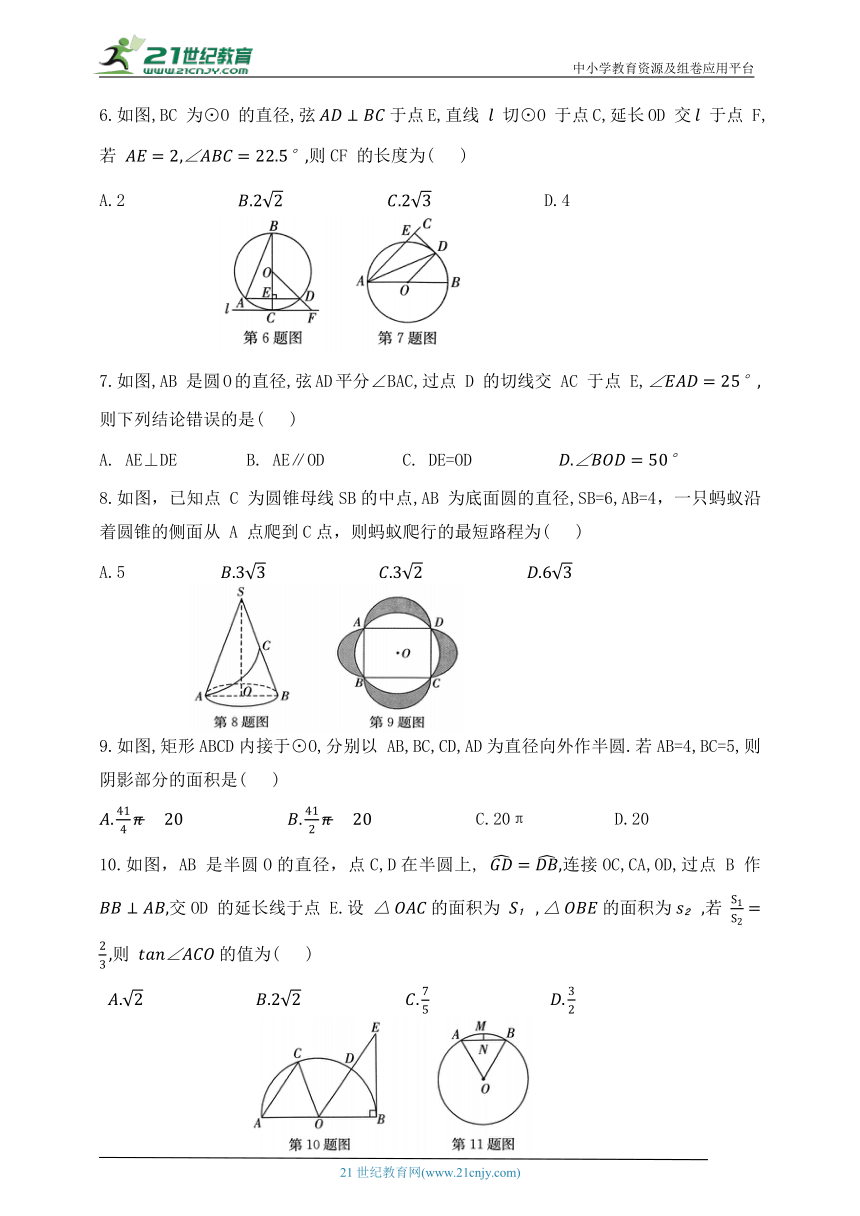
6.如图,BC 为⊙O 的直径,弦于点E,直线 切⊙O 于点C,延长OD 交 于点 F,若 则CF 的长度为( )
A.2 D.4
7.如图,AB 是圆O的直径,弦AD平分∠BAC,过点 D 的切线交 AC 于点 E,则下列结论错误的是( )
A. AE⊥DE B. AE∥OD C. DE=OD
8.如图,已知点 C 为圆锥母线SB的中点,AB 为底面圆的直径,SB=6,AB=4,一只蚂蚁沿着圆锥的侧面从 A 点爬到C点,则蚂蚁爬行的最短路程为( )
A.5
9.如图,矩形ABCD内接于⊙O,分别以 AB,BC,CD,AD为直径向外作半圆.若AB=4,BC=5,则阴影部分的面积是( )
C.20π D.20
10.如图,AB 是半圆O的直径,点C,D在半圆上, 连接OC,CA,OD,过点 B 作 交OD 的延长线于点 E.设 的面积为 的面积为若 则 的值为( )
11.《梦溪笔谈》是我国古代科技著作,其中记录了计算圆弧长度的“会圆术”.如图, 是以点O 为圆心、OA 为半径的圆弧,N 是AB 的中点, “会圆术”给出 的弧长 的近似值计算公式: 当 时,则的值为( )
12.如图,在平面直角坐标系 xOy中,直线 与x轴、y轴分别交于A,B 两点,C,D 是y半径为1的⊙O 上两D动点,且 P为弦CD 的中点.当C,D两点在圆上运B动时, 面积的最大值是( )
A.8 B.6 C.4 D.3
二、填空题
13.如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是___________.
14.如图,将一个量角器与一把无刻度直尺水平摆放,直尺的长边与量角器的外弧分别交于点A,B,C,D,且A,B,C 处的读数分别是 连接 AB,则的度数为____________.
15.如图,点 A 是⊙O 外一点,AB,AC 分别与⊙O 相切于点 B,C,点 D 在上.已知 则 的度数是____________.
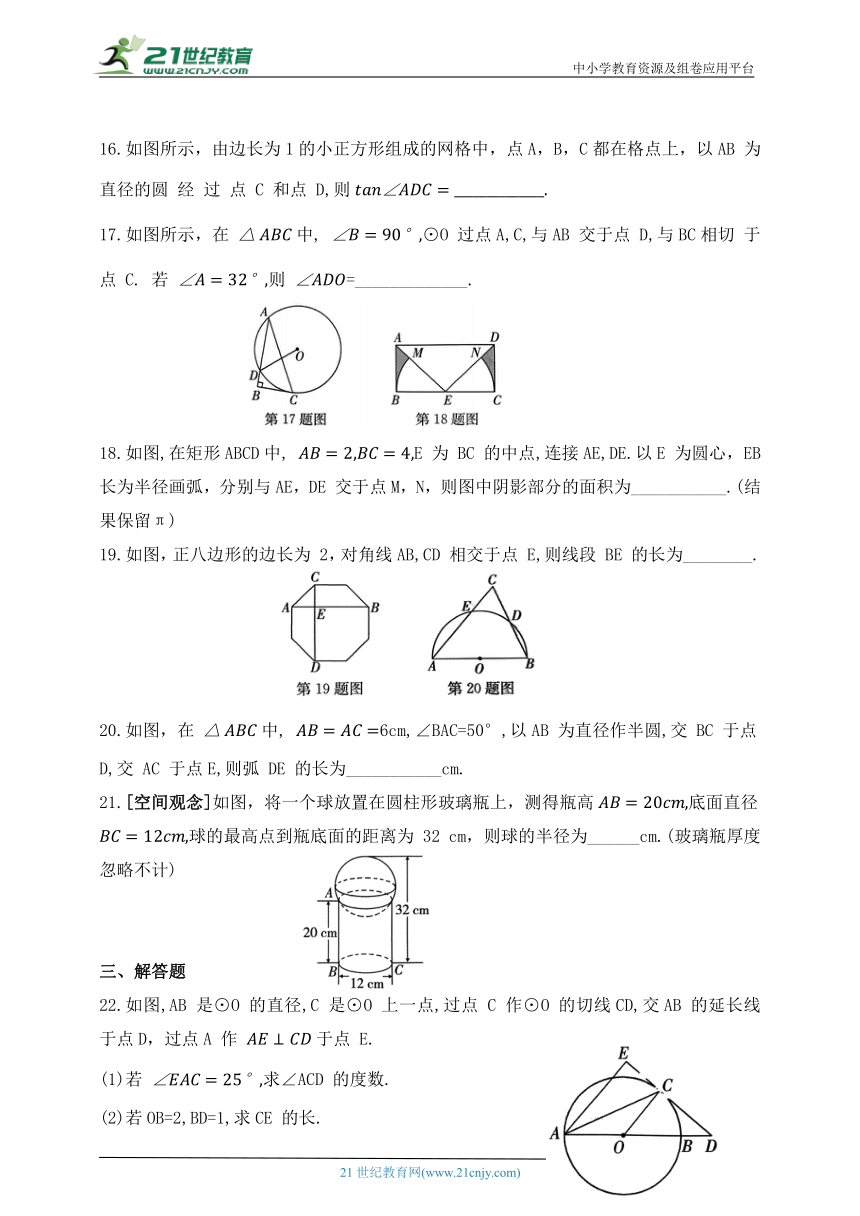
16.如图所示,由边长为1的小正方形组成的网格中,点A,B,C都在格点上,以AB 为直径的圆 经 过 点 C 和点 D,则
17.如图所示,在 中, ⊙O 过点A,C,与AB 交于点 D,与BC相切 于 点 C. 若 则 =_____________.
18.如图,在矩形ABCD中, E 为 BC 的中点,连接AE,DE.以E 为圆心,EB 长为半径画弧,分别与AE,DE 交于点M,N,则图中阴影部分的面积为___________.(结果保留π)
19.如图,正八边形的边长为 2,对角线AB,CD 相交于点 E,则线段 BE 的长为________.
20.如图,在 中, 6cm,∠BAC=50°,以AB 为直径作半圆,交 BC 于点D,交 AC 于点E,则弧 DE 的长为___________cm.
21.[空间观念]如图,将一个球放置在圆柱形玻璃瓶上,测得瓶高底面直径球的最高点到瓶底面的距离为 32 cm,则球的半径为______cm.(玻璃瓶厚度忽略不计)
三、解答题
22.如图,AB 是⊙O 的直径,C 是⊙O 上一点,过点 C 作⊙O 的切线CD,交AB 的延长线于点D,过点A 作 于点 E.
(1)若 求∠ACD 的度数.
(2)若OB=2,BD=1,求CE 的长.
23.已知四边形ABCD内接于⊙O,对角线BD是⊙O的直径.
(1)如图①,连接OA,CA,若 求证:CA 平分
(2)如图②,E 为⊙O 内一点,满足BC, 若 求弦BC的长.
24.如图,AB 是⊙O的直径,AC 是一条弦,D 是弧AC 的中点, 于点E,交 AC 于点F,交⊙O 于点 H,DB 交AC于点 G.
(1)求证:AF=DF.
(2)若 求⊙O 的半径.
25.在⊙O 中,半径OC 垂直于弦AB,垂足为 D, E 为弦AB 所对的优弧上一点.
(1)如图①,求 和 的大小.
(2)如图②,CE 与 AB 相交于点 F, EB,过点 E 作⊙O 的切线,与CO 的延长线相交于点G,若求EG 的长.
26.如图,在菱形ABCD中,对角线AC,BD 相交于点E,⊙O 经过A,D 两点,交对角线 AC 于点 F,连接OF 交 AD 于点G,且AG=GD.
(1)求证:AB 是⊙O 的切线.
(2)已知⊙O 的半径与菱形的边长之比为5:8,求 的值.
27.如图, 内接于⊙ O,过点 B 作 BC 的垂线,交⊙O于点 D,并与CA 的延长线交于点 E,作垂足为M,交⊙O 于点F.
(1)求证:
(2)若⊙O 的半径 求线段 BF的长.
参考答案
1. D 2. D 3. D 4. C 5. C 6. B
7. C [解析]∵弦AD 平分∠BAC,∠EAD=25°,∴∠OAD=∠ODA=25°,∴∠BOD=2∠OAD=50°,故 D正确.∵∠OAD=∠CAD,∴∠CAD=∠ODA,∴OD∥AC,即AE∥OD,故 B正确.∵DE 是⊙O 的切线,∴OD⊥DE,∴AE⊥DE,故 A 正确.如图,过点O作OF⊥AC 于点 F,则四边形OFED 是矩形,∴OF=DE.在Rt△AFO中,OA>OF,又∵OD=OA,∴DE8. B 9. D 10. A 11. B 12. D
13.10 14.52.5° 15.65°
17.64°[解析]如图,连接OC.∵∠A=32°,∴∠DOC=2∠A=64°.∵BC 与⊙O 相切于点C,∴OC⊥BC.∵∠B=90°,∴∠B+∠OCB=180°,∴AB∥OC,∴∠ADO=∠DOC=64°.
18.4-π 19.2+
21.7.5 [解析]如图,设球心为O,过点O作 于点M,连接OA,设球的半径为 r cm.由题意得: OM=(12-r) cm.由垂径定理得: 6cm.在 Rt△OAM中,由勾股定理得 即 解得 r=7.5.
22.解:(1)∵AE⊥CD于点 E,. . (2)∵CD 是⊙O的切线 ∥
23.(1)证明: 即 CA 平分∠BCD. (2)解:如图,延长 AE 交 BC 于点M,延长 CE 交 AB 于点 N.∵AE⊥BC,CE⊥AB,∴∠AMB=∠CNB =90°.∵BD 是 ⊙O 的直径,∠AMB,∴AD∥NC,CD∥AM,∴四边形AECD 是平行四边形,
24.(1)证明:∵D 是弧 AC 的中点, DH,且AB 是⊙O 的直径,
(2)解:∵AB 是⊙O的直径,. 设 AE=x,则DE=2x.∵DF2 或x=0(舍去), ∴⊙O的半径为5.
25.解:(1)∵半径OC 垂直于弦AB, ∠AOC= 60°,∴∠AOB =∠AOC +∠BOC = 120°.
(2)如图,连接OE.∵半径 30°.∵GE 切⊙O 于点E,∴∠OEG=90°,∴tan∠EOG=
26.(1)证明:如图,连接OA,则 OF=OA,∴∠OAF=∵四边形ABCD是菱形,∴∠BAE=∠DAE,∴∠OAB=∠OAF+∠BAE=∠OFA+∠DAE=90°,∴AB⊥OA,∴AB 是⊙O 的切线.
(2)解: 设AG=4m,则OA=5m,∴OF∠AED=∠AGF=90°,∴∠ADB=∠AFG=90°∴tan∠ADB 的值是2.
27.(1)证明:如图,连接 DC,则
(2)解: 为⊙O的直径,. 连接CF,则
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
综合练习
一、选择题
1.如图,点A,B,C,D均在直线上,点 P 在直线外,则经过其中任意三个点,最多可画出圆的个数为( )
A.3 B.4 C.5 D.6
2.如图,⊙O 是 的外接圆,若 则
A.25°
3.如图,正五边形 ABCDE 内接于⊙O,连接 OC,OD,则. ( )
A.60° B.54° C.48° D.36°
4.如图所示,等边△ABC 的顶点A在⊙O 上,边 AB,AC 与⊙O分别交于点D,E,点 F 是劣弧 DE 上一点,且与D,E 不重合,连接 DF,EF,则 的度数为( )
A.115° B.118° C.120°
5.如图,AB切⊙O 于点B,连接OA交⊙O 于点C, ∥交⊙O 于 点D,连接CD,若 则 的度数为( )
6.如图,BC 为⊙O 的直径,弦于点E,直线 切⊙O 于点C,延长OD 交 于点 F,若 则CF 的长度为( )
A.2 D.4
7.如图,AB 是圆O的直径,弦AD平分∠BAC,过点 D 的切线交 AC 于点 E,则下列结论错误的是( )
A. AE⊥DE B. AE∥OD C. DE=OD
8.如图,已知点 C 为圆锥母线SB的中点,AB 为底面圆的直径,SB=6,AB=4,一只蚂蚁沿着圆锥的侧面从 A 点爬到C点,则蚂蚁爬行的最短路程为( )
A.5
9.如图,矩形ABCD内接于⊙O,分别以 AB,BC,CD,AD为直径向外作半圆.若AB=4,BC=5,则阴影部分的面积是( )
C.20π D.20
10.如图,AB 是半圆O的直径,点C,D在半圆上, 连接OC,CA,OD,过点 B 作 交OD 的延长线于点 E.设 的面积为 的面积为若 则 的值为( )
11.《梦溪笔谈》是我国古代科技著作,其中记录了计算圆弧长度的“会圆术”.如图, 是以点O 为圆心、OA 为半径的圆弧,N 是AB 的中点, “会圆术”给出 的弧长 的近似值计算公式: 当 时,则的值为( )
12.如图,在平面直角坐标系 xOy中,直线 与x轴、y轴分别交于A,B 两点,C,D 是y半径为1的⊙O 上两D动点,且 P为弦CD 的中点.当C,D两点在圆上运B动时, 面积的最大值是( )
A.8 B.6 C.4 D.3
二、填空题
13.如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置.要完成这一圆环排列,共需要正五边形的个数是___________.
14.如图,将一个量角器与一把无刻度直尺水平摆放,直尺的长边与量角器的外弧分别交于点A,B,C,D,且A,B,C 处的读数分别是 连接 AB,则的度数为____________.
15.如图,点 A 是⊙O 外一点,AB,AC 分别与⊙O 相切于点 B,C,点 D 在上.已知 则 的度数是____________.
16.如图所示,由边长为1的小正方形组成的网格中,点A,B,C都在格点上,以AB 为直径的圆 经 过 点 C 和点 D,则
17.如图所示,在 中, ⊙O 过点A,C,与AB 交于点 D,与BC相切 于 点 C. 若 则 =_____________.
18.如图,在矩形ABCD中, E 为 BC 的中点,连接AE,DE.以E 为圆心,EB 长为半径画弧,分别与AE,DE 交于点M,N,则图中阴影部分的面积为___________.(结果保留π)
19.如图,正八边形的边长为 2,对角线AB,CD 相交于点 E,则线段 BE 的长为________.
20.如图,在 中, 6cm,∠BAC=50°,以AB 为直径作半圆,交 BC 于点D,交 AC 于点E,则弧 DE 的长为___________cm.
21.[空间观念]如图,将一个球放置在圆柱形玻璃瓶上,测得瓶高底面直径球的最高点到瓶底面的距离为 32 cm,则球的半径为______cm.(玻璃瓶厚度忽略不计)
三、解答题
22.如图,AB 是⊙O 的直径,C 是⊙O 上一点,过点 C 作⊙O 的切线CD,交AB 的延长线于点D,过点A 作 于点 E.
(1)若 求∠ACD 的度数.
(2)若OB=2,BD=1,求CE 的长.
23.已知四边形ABCD内接于⊙O,对角线BD是⊙O的直径.
(1)如图①,连接OA,CA,若 求证:CA 平分
(2)如图②,E 为⊙O 内一点,满足BC, 若 求弦BC的长.
24.如图,AB 是⊙O的直径,AC 是一条弦,D 是弧AC 的中点, 于点E,交 AC 于点F,交⊙O 于点 H,DB 交AC于点 G.
(1)求证:AF=DF.
(2)若 求⊙O 的半径.
25.在⊙O 中,半径OC 垂直于弦AB,垂足为 D, E 为弦AB 所对的优弧上一点.
(1)如图①,求 和 的大小.
(2)如图②,CE 与 AB 相交于点 F, EB,过点 E 作⊙O 的切线,与CO 的延长线相交于点G,若求EG 的长.
26.如图,在菱形ABCD中,对角线AC,BD 相交于点E,⊙O 经过A,D 两点,交对角线 AC 于点 F,连接OF 交 AD 于点G,且AG=GD.
(1)求证:AB 是⊙O 的切线.
(2)已知⊙O 的半径与菱形的边长之比为5:8,求 的值.
27.如图, 内接于⊙ O,过点 B 作 BC 的垂线,交⊙O于点 D,并与CA 的延长线交于点 E,作垂足为M,交⊙O 于点F.
(1)求证:
(2)若⊙O 的半径 求线段 BF的长.
参考答案
1. D 2. D 3. D 4. C 5. C 6. B
7. C [解析]∵弦AD 平分∠BAC,∠EAD=25°,∴∠OAD=∠ODA=25°,∴∠BOD=2∠OAD=50°,故 D正确.∵∠OAD=∠CAD,∴∠CAD=∠ODA,∴OD∥AC,即AE∥OD,故 B正确.∵DE 是⊙O 的切线,∴OD⊥DE,∴AE⊥DE,故 A 正确.如图,过点O作OF⊥AC 于点 F,则四边形OFED 是矩形,∴OF=DE.在Rt△AFO中,OA>OF,又∵OD=OA,∴DE
13.10 14.52.5° 15.65°
17.64°[解析]如图,连接OC.∵∠A=32°,∴∠DOC=2∠A=64°.∵BC 与⊙O 相切于点C,∴OC⊥BC.∵∠B=90°,∴∠B+∠OCB=180°,∴AB∥OC,∴∠ADO=∠DOC=64°.
18.4-π 19.2+
21.7.5 [解析]如图,设球心为O,过点O作 于点M,连接OA,设球的半径为 r cm.由题意得: OM=(12-r) cm.由垂径定理得: 6cm.在 Rt△OAM中,由勾股定理得 即 解得 r=7.5.
22.解:(1)∵AE⊥CD于点 E,. . (2)∵CD 是⊙O的切线 ∥
23.(1)证明: 即 CA 平分∠BCD. (2)解:如图,延长 AE 交 BC 于点M,延长 CE 交 AB 于点 N.∵AE⊥BC,CE⊥AB,∴∠AMB=∠CNB =90°.∵BD 是 ⊙O 的直径,∠AMB,∴AD∥NC,CD∥AM,∴四边形AECD 是平行四边形,
24.(1)证明:∵D 是弧 AC 的中点, DH,且AB 是⊙O 的直径,
(2)解:∵AB 是⊙O的直径,. 设 AE=x,则DE=2x.∵DF2 或x=0(舍去), ∴⊙O的半径为5.
25.解:(1)∵半径OC 垂直于弦AB, ∠AOC= 60°,∴∠AOB =∠AOC +∠BOC = 120°.
(2)如图,连接OE.∵半径 30°.∵GE 切⊙O 于点E,∴∠OEG=90°,∴tan∠EOG=
26.(1)证明:如图,连接OA,则 OF=OA,∴∠OAF=∵四边形ABCD是菱形,∴∠BAE=∠DAE,∴∠OAB=∠OAF+∠BAE=∠OFA+∠DAE=90°,∴AB⊥OA,∴AB 是⊙O 的切线.
(2)解: 设AG=4m,则OA=5m,∴OF∠AED=∠AGF=90°,∴∠ADB=∠AFG=90°∴tan∠ADB 的值是2.
27.(1)证明:如图,连接 DC,则
(2)解: 为⊙O的直径,. 连接CF,则
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
