人教版数学九年级上册 第二十二章 二次函数 学案(无答案)
文档属性
| 名称 | 人教版数学九年级上册 第二十二章 二次函数 学案(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 295.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 00:00:00 | ||
图片预览

文档简介
二次函数总复习
班级: 组号: 姓名:
【课时安排】
1课时
【复习目标】
1. 理解二次函数的概念; 2. 会把二次函数的一般式化为顶点式,确定图象的顶点坐标、对称轴和开口方向,会用描点法画二次函数的图象; 3. 会平移二次函数y=ax2(a≠0)的图象得到二次函数y=a(ax+m)2+k的图象,了解特殊与一般相互联系和转化的思想; 4. 会用待定系数法求二次函数的解析式; 5. 利用二次函数的图象,了解二次函数的增减性,会求二次函数的图象与x轴的交点坐标和函数的最大值、最小值,了解二次函数与一元二次方程和不等式之间的联系。6.用二次函数的相关知识解决实际问题。
一、知识梳理
专题一:二次函数的概念及其相关性质
形如 的函数叫做二次函数。特别注意:最高次项的次数是 且 不等于0.
性质:写出函数+k的相关性质,并思考它是由函数通过怎样的平移得到的?
知识巩固:
1.已知函数是二次函数,其图象开口方向向下,则m=_____,顶点为_____,当x_____0时,y随x的增大而增大,当x_____0时,y随x的增大而减小。
2.抛物线y=(x-2)2+3的对称轴是( )。
A.直线x=-3 B.直线x=3 C.直线x=-2 D.直线x=2
3.把抛物线y=x2+bx+c的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式是y=x2-3x+5,则有( )。
A、B=3,c=7 B.b=-9,c=-15 C.b=3,c=3 D.b=-9,c=21
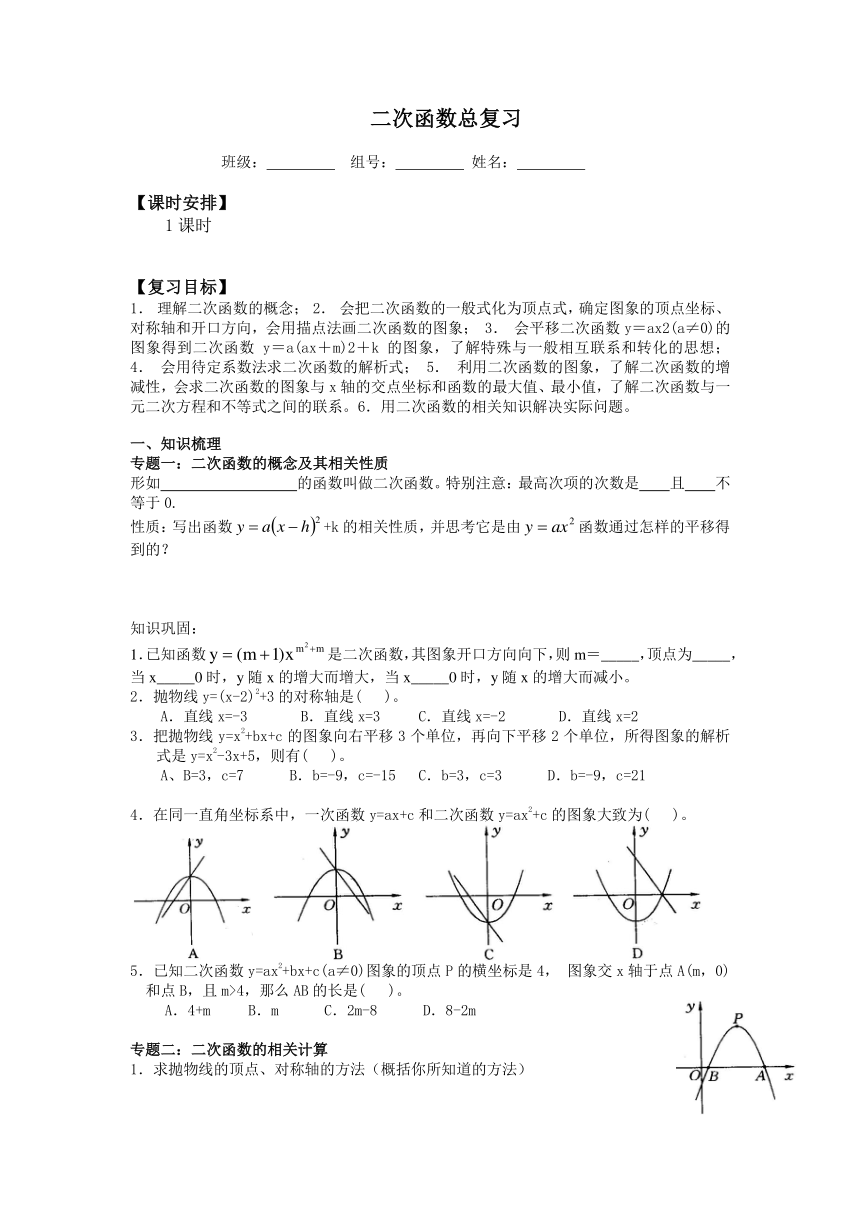
4.在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为( )。
5.已知二次函数y=ax2+bx+c(a≠0)图象的顶点P的横坐标是4,图象交x轴于点A(m,0)和点B,且m>4,那么AB的长是( )。
A.4+m B.m C.2m-8 D.8-2m
专题二:二次函数的相关计算
1.求抛物线的顶点、对称轴的方法(概括你所知道的方法)
2.求二次函数的解析式(写出2种常用的形式)
一般式: 顶点式: 练:
知识巩固:
已知抛物线y=- x2+(6- )x+m-3与x轴有A、B两个交点,且A、B两点关于y轴对称。
(1)求m的值;
(2)写出抛物线解析式及顶点坐标;
(3)根据二次函数与一元二次方程的关系将此题的条件换一种说法写出来。
专题三:二次函数与一元二次方程的关系
1. 已知二次函数y = x2 + (3m -1)x + 2m2 -m,则其图象与x轴( );
A. 一定有两个交点 B. 只有一个交点 C. 没有交点 D. 有一个交点或两个交点
2. 若抛物线y = x2 +2x - m +1与x轴没有交点,则方程x2 + mx +12m -1 = 0的根的情况是( )。
A. 有两个相等的实数根 B. 有两个不相等的实数根 C. 没有实数根 D. 不能确定
专题四:实际应用
一根120cm长的铁丝围成一个矩形,矩形的最大面积为 ;若将其分成两部分,每一部分弯曲成一个正方形,那么两个正方形的面积和最小为 。
二、综合运用
1.如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于A点。
(1)根据图象确定a、b、c的符号,并说明理由;
(2)如果点A的坐标为(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数的解析式。
2.某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱。
(1)求平均每天销售量(箱)与销售价(元/箱)之间的函数关系式。
(2)求该批发商平均每天的销售利润(元)与销售价(元/箱)之间的函数关系式。
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
三、课堂检测
1.若将二次函数y=x2-2x+3配方为y=(x-h)2+k的形式,则 y=_______。
2.请你写出函数y=(x+1)2与y=x2+1具有的一个共同性质_______。
3.二次函数y=x2+x-1,当x=______时,y有最_____值,这个值是____。
4.已知二次函数的图象开口向下,且与y轴的正半轴相交,请你写出一个满足条件的二次函数的解析式:_________。
5.已知抛物线y=ax2+x+c与x轴交点的横坐标为-1,则a+c=_____。
6.已知函数y=x2+bx-1的图象经过点(3,2)。
(1)求这个函数的解析式;
(2)画出它的图象,并指出图象的顶点坐标;
(3)当x>0时,求使y≥2的x取值范围。
四、课堂小结
1.二次函数的图象与性质;2.二次函数的图象的平移;3.二次函数的解析式的确定及应用;
五、拓展探究
如图,在直角坐标系中,正方形ABCD的边长为a,O为原点,点B在x轴的负半轴上,点D在y轴的正半轴上。直线OE的解析式为y=2x,直线CF过x轴上一点C(-a,0)且与OE平行。现正方形以每秒的速度匀速沿x轴正方向平行移动,设运动时间为t秒,正方形被夹在直线OE和CF间的部分的面积为S。
(1)当0≤t<4时,写出S与t的函数关系;
(2)当4≤t≤5时,写出S与t的函数关系,在这个范围内S有无最大值?若有,请求出最大值;若没有,请说明理由。
班级: 组号: 姓名:
【课时安排】
1课时
【复习目标】
1. 理解二次函数的概念; 2. 会把二次函数的一般式化为顶点式,确定图象的顶点坐标、对称轴和开口方向,会用描点法画二次函数的图象; 3. 会平移二次函数y=ax2(a≠0)的图象得到二次函数y=a(ax+m)2+k的图象,了解特殊与一般相互联系和转化的思想; 4. 会用待定系数法求二次函数的解析式; 5. 利用二次函数的图象,了解二次函数的增减性,会求二次函数的图象与x轴的交点坐标和函数的最大值、最小值,了解二次函数与一元二次方程和不等式之间的联系。6.用二次函数的相关知识解决实际问题。
一、知识梳理
专题一:二次函数的概念及其相关性质
形如 的函数叫做二次函数。特别注意:最高次项的次数是 且 不等于0.
性质:写出函数+k的相关性质,并思考它是由函数通过怎样的平移得到的?
知识巩固:
1.已知函数是二次函数,其图象开口方向向下,则m=_____,顶点为_____,当x_____0时,y随x的增大而增大,当x_____0时,y随x的增大而减小。
2.抛物线y=(x-2)2+3的对称轴是( )。
A.直线x=-3 B.直线x=3 C.直线x=-2 D.直线x=2
3.把抛物线y=x2+bx+c的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式是y=x2-3x+5,则有( )。
A、B=3,c=7 B.b=-9,c=-15 C.b=3,c=3 D.b=-9,c=21
4.在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为( )。
5.已知二次函数y=ax2+bx+c(a≠0)图象的顶点P的横坐标是4,图象交x轴于点A(m,0)和点B,且m>4,那么AB的长是( )。
A.4+m B.m C.2m-8 D.8-2m
专题二:二次函数的相关计算
1.求抛物线的顶点、对称轴的方法(概括你所知道的方法)
2.求二次函数的解析式(写出2种常用的形式)
一般式: 顶点式: 练:
知识巩固:
已知抛物线y=- x2+(6- )x+m-3与x轴有A、B两个交点,且A、B两点关于y轴对称。
(1)求m的值;
(2)写出抛物线解析式及顶点坐标;
(3)根据二次函数与一元二次方程的关系将此题的条件换一种说法写出来。
专题三:二次函数与一元二次方程的关系
1. 已知二次函数y = x2 + (3m -1)x + 2m2 -m,则其图象与x轴( );
A. 一定有两个交点 B. 只有一个交点 C. 没有交点 D. 有一个交点或两个交点
2. 若抛物线y = x2 +2x - m +1与x轴没有交点,则方程x2 + mx +12m -1 = 0的根的情况是( )。
A. 有两个相等的实数根 B. 有两个不相等的实数根 C. 没有实数根 D. 不能确定
专题四:实际应用
一根120cm长的铁丝围成一个矩形,矩形的最大面积为 ;若将其分成两部分,每一部分弯曲成一个正方形,那么两个正方形的面积和最小为 。
二、综合运用
1.如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于A点。
(1)根据图象确定a、b、c的符号,并说明理由;
(2)如果点A的坐标为(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数的解析式。
2.某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱。
(1)求平均每天销售量(箱)与销售价(元/箱)之间的函数关系式。
(2)求该批发商平均每天的销售利润(元)与销售价(元/箱)之间的函数关系式。
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
三、课堂检测
1.若将二次函数y=x2-2x+3配方为y=(x-h)2+k的形式,则 y=_______。
2.请你写出函数y=(x+1)2与y=x2+1具有的一个共同性质_______。
3.二次函数y=x2+x-1,当x=______时,y有最_____值,这个值是____。
4.已知二次函数的图象开口向下,且与y轴的正半轴相交,请你写出一个满足条件的二次函数的解析式:_________。
5.已知抛物线y=ax2+x+c与x轴交点的横坐标为-1,则a+c=_____。
6.已知函数y=x2+bx-1的图象经过点(3,2)。
(1)求这个函数的解析式;
(2)画出它的图象,并指出图象的顶点坐标;
(3)当x>0时,求使y≥2的x取值范围。
四、课堂小结
1.二次函数的图象与性质;2.二次函数的图象的平移;3.二次函数的解析式的确定及应用;
五、拓展探究
如图,在直角坐标系中,正方形ABCD的边长为a,O为原点,点B在x轴的负半轴上,点D在y轴的正半轴上。直线OE的解析式为y=2x,直线CF过x轴上一点C(-a,0)且与OE平行。现正方形以每秒的速度匀速沿x轴正方向平行移动,设运动时间为t秒,正方形被夹在直线OE和CF间的部分的面积为S。
(1)当0≤t<4时,写出S与t的函数关系;
(2)当4≤t≤5时,写出S与t的函数关系,在这个范围内S有无最大值?若有,请求出最大值;若没有,请说明理由。
同课章节目录
