人教版数学九年级上册 23.1 图形的旋转 (1-3课时)学案(无答案)
文档属性
| 名称 | 人教版数学九年级上册 23.1 图形的旋转 (1-3课时)学案(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 268.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 17:10:21 | ||
图片预览

文档简介
图形的旋转
班级: 姓名: 组号:
【课时安排】
3课时
(
图1
) 第一课时
一、旧知回顾
1.如图1,△DEF是等边三角形ABC沿从B到C的方向平移得到的。
(1)平移的距离是线段_____的长度;(2)AB∥_____,AB=_____;
(3)∠B与_____是对应角;
2.如图2,△ABC与△A1B1C1关于直线L对称,将△A1B1C1向右平移得到△A2B2C2,
(
图2
)由此得出下列判断:①AB∥A2B2;②∠A=∠A2;③AB=A2B2,其中正确的是( )
A.①② B.②③ C.①③ D.①②③
【新知探究】
4.请举出一个生活中与旋转相关的实例,你能得到旋转的概念是什么?
旋转的概念:
5.在旋转中必须具备 要素:
6.如何快速地找出对应点、对应线段、对应角,以下图为例说明:
(
图3
)如图3,将△AOB逆时针旋转45°到新位置△A′OB′,从图中,可以看到点A旋转到点A′, OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段与角。你还能写出其它的对应关系吗?
思考:△AOB的边OB的中点D的对应点在哪里?
归纳旋转的性质:
(
图4
)试一试
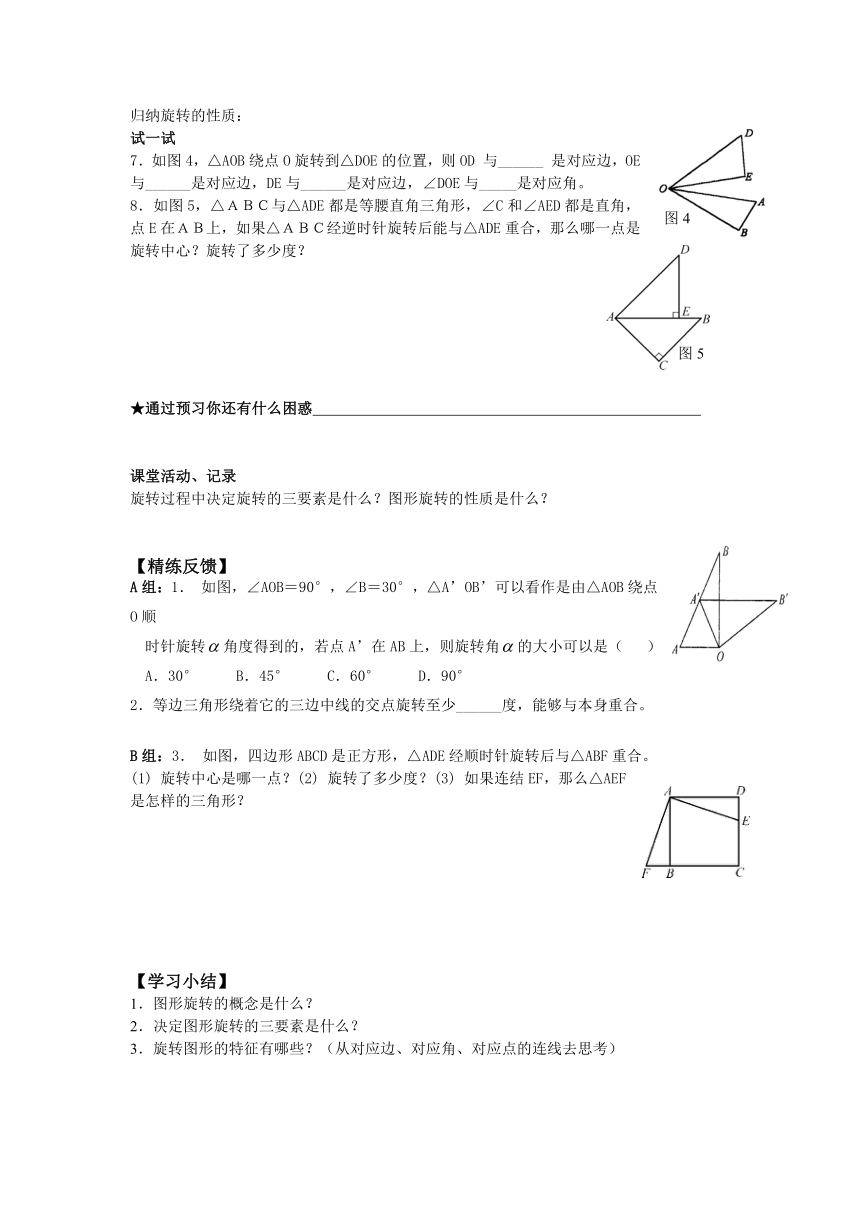
7.如图4,△AOB绕点O旋转到△DOE的位置,则OD与______是对应边,OE与______是对应边,DE与______是对应边,∠DOE与_____是对应角。
(
图5
)8.如图5,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经逆时针旋转后能与△ADE重合,那么哪一点是旋转中心?旋转了多少度?
★通过预习你还有什么困惑
课堂活动、记录
旋转过程中决定旋转的三要素是什么?图形旋转的性质是什么?
【精练反馈】
A组:1. 如图,∠AOB=90°,∠B=30°,△A’OB’可以看作是由△AOB绕点O顺
时针旋转角度得到的,若点A’在AB上,则旋转角的大小可以是( )
A.30° B.45° C.60° D.90°
2.等边三角形绕着它的三边中线的交点旋转至少______度,能够与本身重合。
B组:3. 如图,四边形ABCD是正方形,△ADE经顺时针旋转后与△ABF重合。
(1) 旋转中心是哪一点?(2) 旋转了多少度?(3) 如果连结EF,那么△AEF是怎样的三角形?
【学习小结】
1.图形旋转的概念是什么?
2.决定图形旋转的三要素是什么?
3.旋转图形的特征有哪些?(从对应边、对应角、对应点的连线去思考)
【拓展延伸】
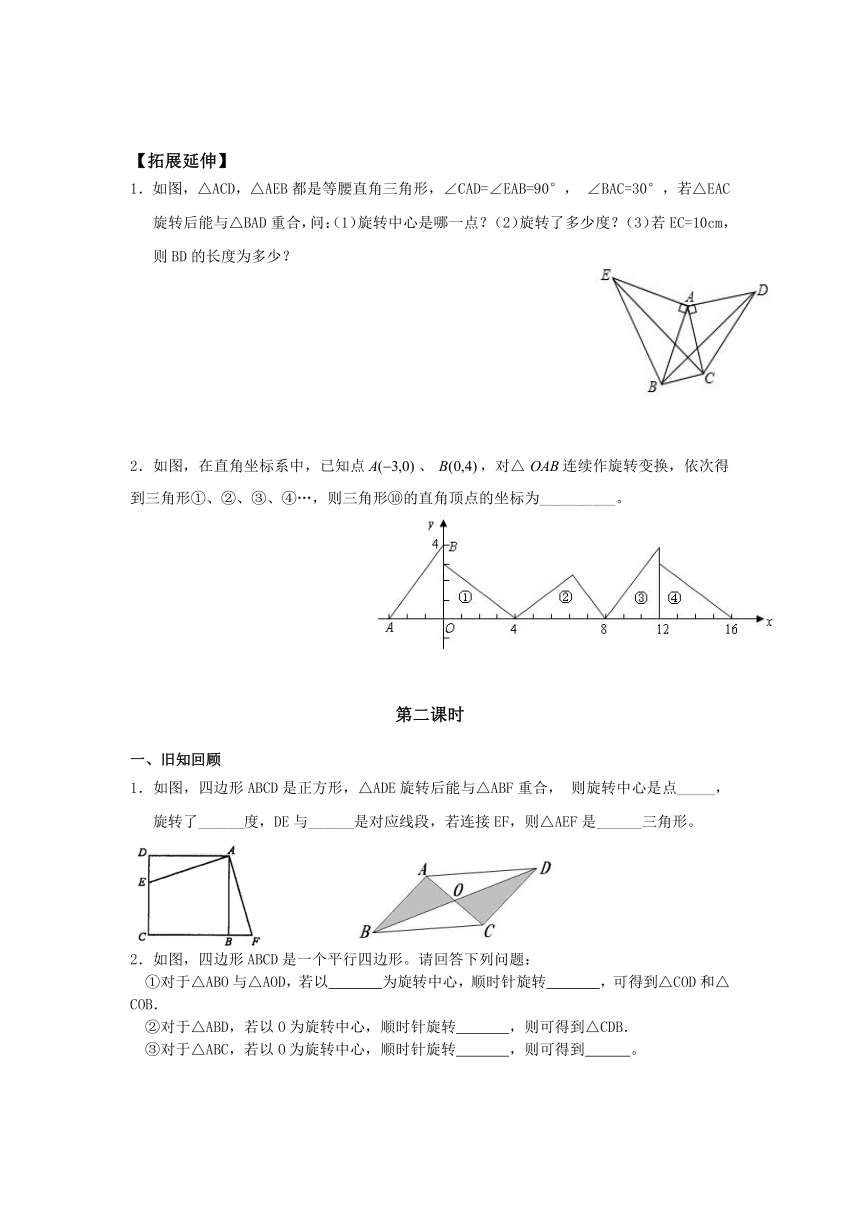
1.如图,△ACD,△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,∠BAC=30°,若△EAC旋转后能与△BAD重合,问:(1)旋转中心是哪一点?(2)旋转了多少度?(3)若EC=10cm,则BD的长度为多少?
2.如图,在直角坐标系中,已知点、,对△连续作旋转变换,依次得到三角形①、②、③、④…,则三角形⑩的直角顶点的坐标为__________。
第二课时
一、旧知回顾
1.如图,四边形ABCD是正方形,△ADE旋转后能与△ABF重合,则旋转中心是点_____,旋转了______度,DE与______是对应线段,若连接EF,则△AEF是______三角形。
2.如图,四边形ABCD是一个平行四边形。请回答下列问题:
①对于△ABO与△AOD,若以 为旋转中心,顺时针旋转 ,可得到△COD和△COB.
②对于△ABD,若以O为旋转中心,顺时针旋转 ,则可得到△CDB.
③对于△ABC,若以O为旋转中心,顺时针旋转 ,则可得到 。
【新知探究】
(1)如图方格中△ABC,按要求作图①点A绕着点C顺时针旋转90度;③线段AB绕着点C逆时针旋转180度;④△ABC绕着点C逆时针旋转90度;
6. 旋转的画法:请归纳一个图形按要求作旋转后的图形的方法?
试一试
5.如图,△ABO绕点O旋转了30°至△DCO,那么∠AOD=____度,
连结AD, △AOD是______三角形, ∠OAD的度数为____。
6.已知:如图,四边形ABCD及一点P。
求作:四边形A′B′C′D′,使得它是由四边形ABCD绕P点顺时针旋转150°得到的。
★通过预习你还有什么困惑
(
课堂探究
)课堂活动、记录
1. 画旋转图形的步骤有哪些?
【精练反馈】
A组:1. 如图,将△ABC绕点A旋转后得到△ADE,则旋转方式是( )。
A.顺时针旋转90° B.逆时针旋转90° C.顺时针旋转45° D.逆时针旋转45°
2.确定图中五角星的旋转中心,它可以看成是由哪个基本图形旋转而生成的,旋转几次,每一次旋转多少度。
B组:3.画出所给图形绕点O顺时针旋转90°后的图形。旋转几次后可以与原图形重合?
(第1题) (第2题) (第3题)
【学习小结】
画旋转图形的步骤有哪些?
【拓展延伸】
1.如图,把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6cm,DC=7cm,把三角板DCE绕点C顺时针旋转15°得到如图乙。这时AB与CD’相交于点O,D’E’与AB相交于点F。
(
(甲)
(乙)
)①求的度数;
②求线段AD’的长。
2.已知:如图,若线段CD是由线段AB经过旋转变换得到的。
求作:旋转中心O点。
第三课时
一、巩固训练
1.如图1,将△ABC绕点A旋转后得到△ADE,则旋转方式是( )
A.顺时针旋转90° B.逆时针旋转90° C.顺时针旋转45° D.逆时针旋转45°
2.如图2是一个旋转对称图形,要使它旋转后与自身重合,应将它绕中心逆时针方向旋转的
度数至少为( )度。
A.30 o B.45 o C.60 o D.90 o
3.如图3,图形旋转一定角度后能与自身重合,则旋转的角度可能是( )
(
图1
图2
图3
图4
) A.300 B.600 C.900 D.1200
4.如图4,把三角形△ABC绕着点C顺时针旋转350,得到△A'B'C,A'B'交AC于点D,若∠A'DC=900,则∠A的度数是__________。
二、错题再现
1.图5有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,那么图中阴影部分的面积是( )。
A.4cm2 B.8cm2 C.16cm2 D.无法确定
2.如图6,将△ABC绕点A旋转一定角度后能与△ADE重合,如果△ABC的面积是12cm2 ,
那么△ADE的面积是 。
(
图6
图7
图5
图8
)3.如图7,△ABC绕点B逆时针方向旋转到△EBD的位置,若∠E=210,∠C=180,E,B,C在同一直线上,则旋转角的度数是__________。
4.如图8所示,已知正方形ABCD中的△DCF可以经过旋转得到△ECB.
(1)图中哪一个点是旋转中心?
(2)按什么方向旋转了多少度?
(3)如果CF=3cm,求EF的长。
三、能力提升
1.已知:如图,在△ABC中,AB=AC,∠BAC=α,且60°<α<120°,P为△ABC内部一点,且PC=AC,∠PCA=120°﹣α。
①用含α的代数式表示∠APC;
②求证:∠BAP=∠PCB;
③求∠PBC的度数。
四、精练反馈
1.如图,△AOB旋转到△A′OB′的位置。若∠AOA′=90°,则旋转中心是点______。旋转角是______。点A的对应点是______。线段AB的对应线段是______。∠B的对应角是______。∠BOB′=______。
1题图 2题图
2.如图,△ABC绕着点O旋转到△DEF的位置,则旋转中心是______。旋转角是______。AO=______,AB=______,∠ACB=∠______。
3.图11,点D是等边△ABC内一点,若△ABD绕点A逆时针旋转后能与△ACE重合,则旋转了____度。
4. 已知正方形ABCD中,点E在边DC上,DE=2,EC=1(如图所示)把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为
(
图11
图12
)
班级: 姓名: 组号:
【课时安排】
3课时
(
图1
) 第一课时
一、旧知回顾
1.如图1,△DEF是等边三角形ABC沿从B到C的方向平移得到的。
(1)平移的距离是线段_____的长度;(2)AB∥_____,AB=_____;
(3)∠B与_____是对应角;
2.如图2,△ABC与△A1B1C1关于直线L对称,将△A1B1C1向右平移得到△A2B2C2,
(
图2
)由此得出下列判断:①AB∥A2B2;②∠A=∠A2;③AB=A2B2,其中正确的是( )
A.①② B.②③ C.①③ D.①②③
【新知探究】
4.请举出一个生活中与旋转相关的实例,你能得到旋转的概念是什么?
旋转的概念:
5.在旋转中必须具备 要素:
6.如何快速地找出对应点、对应线段、对应角,以下图为例说明:
(
图3
)如图3,将△AOB逆时针旋转45°到新位置△A′OB′,从图中,可以看到点A旋转到点A′, OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段与角。你还能写出其它的对应关系吗?
思考:△AOB的边OB的中点D的对应点在哪里?
归纳旋转的性质:
(
图4
)试一试
7.如图4,△AOB绕点O旋转到△DOE的位置,则OD与______是对应边,OE与______是对应边,DE与______是对应边,∠DOE与_____是对应角。
(
图5
)8.如图5,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经逆时针旋转后能与△ADE重合,那么哪一点是旋转中心?旋转了多少度?
★通过预习你还有什么困惑
课堂活动、记录
旋转过程中决定旋转的三要素是什么?图形旋转的性质是什么?
【精练反馈】
A组:1. 如图,∠AOB=90°,∠B=30°,△A’OB’可以看作是由△AOB绕点O顺
时针旋转角度得到的,若点A’在AB上,则旋转角的大小可以是( )
A.30° B.45° C.60° D.90°
2.等边三角形绕着它的三边中线的交点旋转至少______度,能够与本身重合。
B组:3. 如图,四边形ABCD是正方形,△ADE经顺时针旋转后与△ABF重合。
(1) 旋转中心是哪一点?(2) 旋转了多少度?(3) 如果连结EF,那么△AEF是怎样的三角形?
【学习小结】
1.图形旋转的概念是什么?
2.决定图形旋转的三要素是什么?
3.旋转图形的特征有哪些?(从对应边、对应角、对应点的连线去思考)
【拓展延伸】
1.如图,△ACD,△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,∠BAC=30°,若△EAC旋转后能与△BAD重合,问:(1)旋转中心是哪一点?(2)旋转了多少度?(3)若EC=10cm,则BD的长度为多少?
2.如图,在直角坐标系中,已知点、,对△连续作旋转变换,依次得到三角形①、②、③、④…,则三角形⑩的直角顶点的坐标为__________。
第二课时
一、旧知回顾
1.如图,四边形ABCD是正方形,△ADE旋转后能与△ABF重合,则旋转中心是点_____,旋转了______度,DE与______是对应线段,若连接EF,则△AEF是______三角形。
2.如图,四边形ABCD是一个平行四边形。请回答下列问题:
①对于△ABO与△AOD,若以 为旋转中心,顺时针旋转 ,可得到△COD和△COB.
②对于△ABD,若以O为旋转中心,顺时针旋转 ,则可得到△CDB.
③对于△ABC,若以O为旋转中心,顺时针旋转 ,则可得到 。
【新知探究】
(1)如图方格中△ABC,按要求作图①点A绕着点C顺时针旋转90度;③线段AB绕着点C逆时针旋转180度;④△ABC绕着点C逆时针旋转90度;
6. 旋转的画法:请归纳一个图形按要求作旋转后的图形的方法?
试一试
5.如图,△ABO绕点O旋转了30°至△DCO,那么∠AOD=____度,
连结AD, △AOD是______三角形, ∠OAD的度数为____。
6.已知:如图,四边形ABCD及一点P。
求作:四边形A′B′C′D′,使得它是由四边形ABCD绕P点顺时针旋转150°得到的。
★通过预习你还有什么困惑
(
课堂探究
)课堂活动、记录
1. 画旋转图形的步骤有哪些?
【精练反馈】
A组:1. 如图,将△ABC绕点A旋转后得到△ADE,则旋转方式是( )。
A.顺时针旋转90° B.逆时针旋转90° C.顺时针旋转45° D.逆时针旋转45°
2.确定图中五角星的旋转中心,它可以看成是由哪个基本图形旋转而生成的,旋转几次,每一次旋转多少度。
B组:3.画出所给图形绕点O顺时针旋转90°后的图形。旋转几次后可以与原图形重合?
(第1题) (第2题) (第3题)
【学习小结】
画旋转图形的步骤有哪些?
【拓展延伸】
1.如图,把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6cm,DC=7cm,把三角板DCE绕点C顺时针旋转15°得到如图乙。这时AB与CD’相交于点O,D’E’与AB相交于点F。
(
(甲)
(乙)
)①求的度数;
②求线段AD’的长。
2.已知:如图,若线段CD是由线段AB经过旋转变换得到的。
求作:旋转中心O点。
第三课时
一、巩固训练
1.如图1,将△ABC绕点A旋转后得到△ADE,则旋转方式是( )
A.顺时针旋转90° B.逆时针旋转90° C.顺时针旋转45° D.逆时针旋转45°
2.如图2是一个旋转对称图形,要使它旋转后与自身重合,应将它绕中心逆时针方向旋转的
度数至少为( )度。
A.30 o B.45 o C.60 o D.90 o
3.如图3,图形旋转一定角度后能与自身重合,则旋转的角度可能是( )
(
图1
图2
图3
图4
) A.300 B.600 C.900 D.1200
4.如图4,把三角形△ABC绕着点C顺时针旋转350,得到△A'B'C,A'B'交AC于点D,若∠A'DC=900,则∠A的度数是__________。
二、错题再现
1.图5有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,那么图中阴影部分的面积是( )。
A.4cm2 B.8cm2 C.16cm2 D.无法确定
2.如图6,将△ABC绕点A旋转一定角度后能与△ADE重合,如果△ABC的面积是12cm2 ,
那么△ADE的面积是 。
(
图6
图7
图5
图8
)3.如图7,△ABC绕点B逆时针方向旋转到△EBD的位置,若∠E=210,∠C=180,E,B,C在同一直线上,则旋转角的度数是__________。
4.如图8所示,已知正方形ABCD中的△DCF可以经过旋转得到△ECB.
(1)图中哪一个点是旋转中心?
(2)按什么方向旋转了多少度?
(3)如果CF=3cm,求EF的长。
三、能力提升
1.已知:如图,在△ABC中,AB=AC,∠BAC=α,且60°<α<120°,P为△ABC内部一点,且PC=AC,∠PCA=120°﹣α。
①用含α的代数式表示∠APC;
②求证:∠BAP=∠PCB;
③求∠PBC的度数。
四、精练反馈
1.如图,△AOB旋转到△A′OB′的位置。若∠AOA′=90°,则旋转中心是点______。旋转角是______。点A的对应点是______。线段AB的对应线段是______。∠B的对应角是______。∠BOB′=______。
1题图 2题图
2.如图,△ABC绕着点O旋转到△DEF的位置,则旋转中心是______。旋转角是______。AO=______,AB=______,∠ACB=∠______。
3.图11,点D是等边△ABC内一点,若△ABD绕点A逆时针旋转后能与△ACE重合,则旋转了____度。
4. 已知正方形ABCD中,点E在边DC上,DE=2,EC=1(如图所示)把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为
(
图11
图12
)
同课章节目录
