人教版数学九年级上册 第二十三章 旋转——半角模型的应用 学案(表格式)
文档属性
| 名称 | 人教版数学九年级上册 第二十三章 旋转——半角模型的应用 学案(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 00:00:00 | ||
图片预览



文档简介
旋转复习
——半角模型的应用
人民教育出版社 初中数学 九年级上册 第二十三章
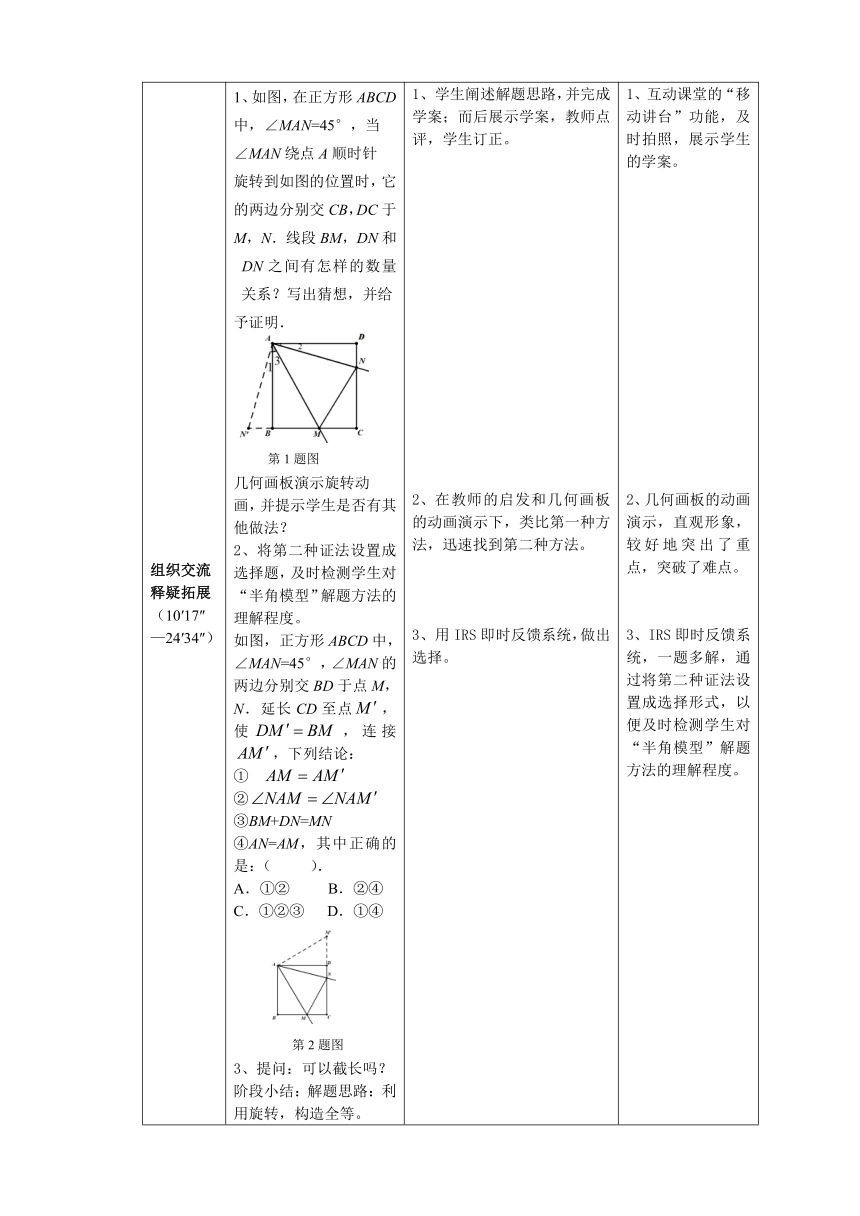
教材分析 “旋转变换”是初中图形变换中的一个重要内容,本节课是在学生学完了第二十三章《旋转》后的复习课,旨在帮助学生进一步理解旋转的概念和性质,并能用旋转变换深入理解“半角模型”。
学情分析 学生已经学移变换、轴对称变换、旋转变换这三个重要的图形变换,对几何图形已经具备了一定的认识,但是还缺乏一定的动态认识,对于在复杂图形中利用旋转变换解决问题,还存在一定难度。
教学目标 知识与技能 复习旋转的概念与性质;掌握利用旋转,构造全等的解题思路。
过程与方法 1、在问题的探讨中,通过一题多解,培养分析问题,多角度看待问题的能力;2、借助智慧课堂(网络空间的“教学助手”“互动课堂”“家校帮”、Hiteach软件、几何画板)等信息技术的使用,提高教与学的有效性、高效性。
情感、态度与价值观 在分组讨论、合作交流中,培养学生善于观察、勇于探索和勤于思考、合作交流的能力;体会从特殊到一般、转化等数学思想。
教学重点 复习旋转的概念与性质 简述解决重、难点的措施 课前推送微课和习题,让学生复习旋转的概念与性质,并完成自我检测,课堂复习环节,进一步通过检测形式,让学生继续复习旋转的概念与性质,突出重点。
教学难点 掌握利用旋转,构造全等的解题思路。 借助几何画板演示旋转动画,让学生直观感受旋转变换,突破难点,通过HITEACH的即时反馈、网络空间的拍照展示等功能,及时了解学情,进一步突破难点。
教学环境 云端一体互动课堂(“教学助手”课前推送导学单、“互动课堂”进行授课、“教学助手”课后推送课堂实录、思考题、课后检测题,学生登录“家校帮”观看微课、完成课前导学和课后思考题及检测。) 教学方法 自主合作探究与启发引导相结合
教学过程
教学环节 教师活动 学生活动 媒体作用及分析
推送导学自主学习(前一天晚上+课前)(0′06″—0′27″) 课前推送导学单(微课、课前检测题),提前了解学情,以学定教。 通过观看微课,复习旋转的概念与性质,并且初步认识半角模型的解题思路,完成习题,进行自我检测。 通过网络空间的“教学助手”推送导学单(微课、课前检测题),提前了解学情,以调整教学策略,实现以学定教的目的。
复习旧知检测反馈(0′28″—10′16″) 复习旋转概念与性质讲评课前导学情况;如图,△ABC和△ADE均为正三角形,则图中可看作是旋转关系的三角形是( ).△ABC和△ADE B.△ABC和△ABD C.△ABD和△ACE D.△ACE和△ADE4、如图,△ABC和△ADE都是等腰三角形,AB=AC,AD=AE,且∠DAE= ∠BAC,若∠DBA=25°,则∠ECA=( ).A.30° B.25° C.20° D.5°5、如图,△ADN是直角三角形,将△ADN绕点A顺时针旋转90°后,能与△ABE重合,如果AN=4,那么EN=______. 根据图形,复习旋转的概念和性质。让学生进行自我纠正。使用互动课堂的随机挑人功能,检测基本知识点的掌握情况。用HITEACH TBL2的IRS即时反馈,检测学生的知识运用情况。5、使用抢答功能,进一步巩固旧知。 让学生对导学单里的题目进行自我纠正,进一步加深学生对旋转概念、性质的理解;互动课堂的随机挑人,可以保证所有学生都有机会被抽到,能较客观地反映学生对基础知识的掌握情况;IRS即时反馈,能及时检测学生的知识运用情况,便于教师及时调整教学策略;使用抢答功能,进一步巩固旧知的同时,也能激发学生的学习兴趣。
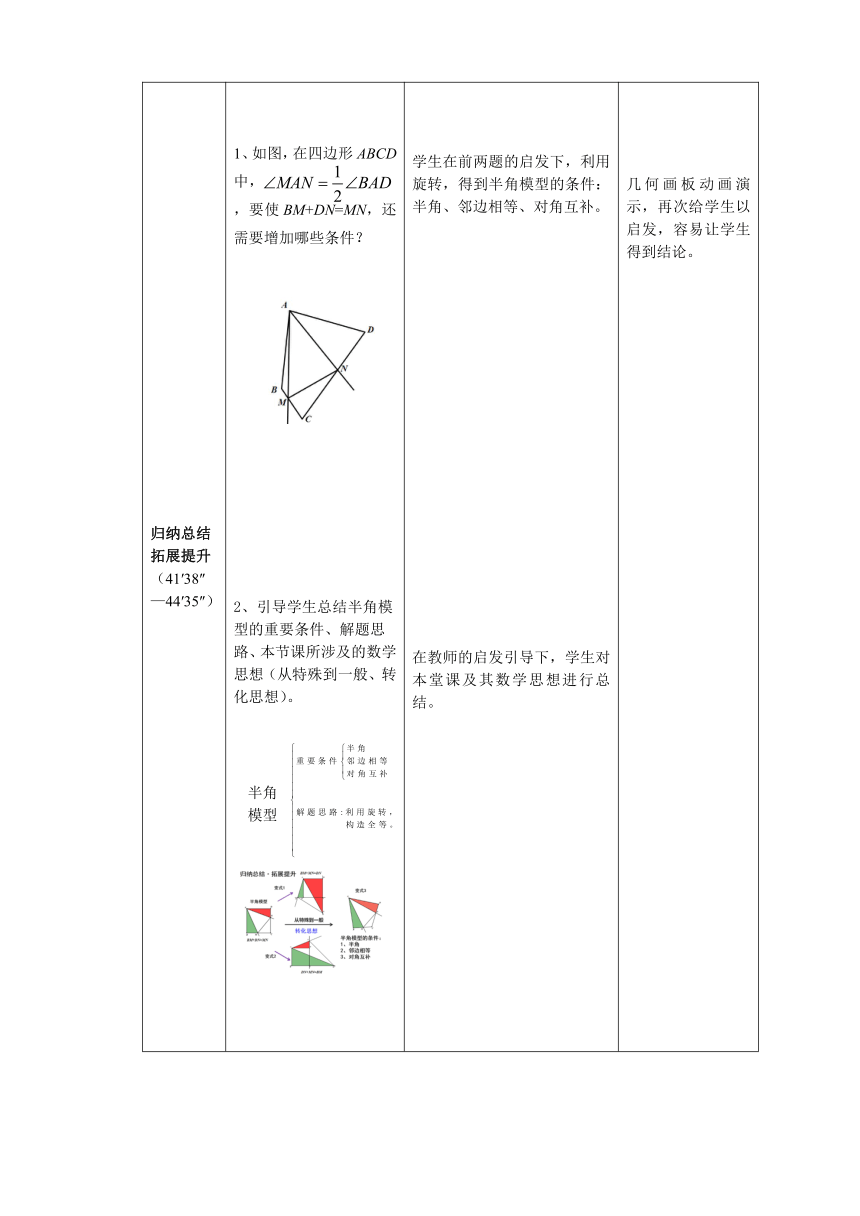
组织交流释疑拓展(10′17″—24′34″) 1、如图,在正方形ABCD 中,∠MAN=45°,当 ∠MAN绕点A顺时针 旋转到如图的位置时,它的 的两边分别交CB,DC于点 M,N.线段BM,DN和M DN之间有怎样的数量关 关系?写出猜想,并给 予证明.几何画板演示旋转动画,并提示学生是否有其他做法?2、将第二种证法设置成选择题,及时检测学生对
“半角模型”解题方法的理解程度。如图,正方形ABCD中,∠MAN=45°,∠MAN的两边分别交BD于点M,N.延长CD至点,使,连接,下列结论:① ②③BM+DN=MN ④AN=AM,其中正确的是:( ).A.①② B.②④ C.①②③ D.①④3、提问:可以截长吗?阶段小结:解题思路:利用旋转,构造全等。 学生阐述解题思路,并完成学案;而后展示学案,教师点评,学生订正。在教师的启发和几何画板的动画演示下,类比第一种方法,迅速找到第二种方法。用IRS即时反馈系统,做出选择。 1、互动课堂的“移动讲台”功能,及时拍照,展示学生的学案。2、几何画板的动画演示,直观形象,较好地突出了重点,突破了难点。3、IRS即时反馈系统,一题多解,通过将第二种证法设置成选择形式,以便及时检测学生对“半角模型”解题方法的理解程度。
变式教学检测反馈(24′35″—41′37″) (变式1)如图,正方形ABCD中,∠MAN=45°,当∠MAN绕点A顺时针旋转到如图的位置时,它的两边分别交CB,DC的延长线于点M,N.线段BM,DN和MN之间有怎样的数量关系?写出猜想,并给予证明.引导学生动手测量(测量前,几何画板演示AN与BC的交点的情况),得到猜想,接着类比前两种方法进行解题,同时用几何画板演示动画演示突破难点。2、(变式2·课后思考)如图,正方形ABCD中,∠MAN=45°,当∠MAN绕点A逆时针旋转到如图的位置时,它的两边分别交CB,DC的反向延长线于点M,N.线段BM,DN和MN之间有怎样的数量关系?写出猜想,并给予证明. 第一、二两组的同学采用第一种方法进行证明;四两组的同学采用第二种方法进行证明。四人讨论,学生上台讲题,培养学生合作交流、自主探究的能力。学生在课后完成这道思考题。 用几何画板演示图形的变化过程,进行变式教学,让整堂复习课脉络清晰。互动课堂的“移动讲台”功能,及时将学生的解题思路拍照上传,学生上台利用互动课堂进行白板放大和书写,方便清晰,效果很好。利用家校帮推送这道思考题,及时有效。
归纳总结拓展提升(41′38″—44′35″) 1、如图,在四边形ABCD中,,要使BM+DN=MN,还需要增加哪些条件?引导学生总结半角模型的重要条件、解题思路、本节课所涉及的数学思想(从特殊到一般、转化思想)。 学生在前两题的启发下,利用旋转,得到半角模型的条件:半角、邻边相等、对角互补。在教师的启发引导下,学生对本堂课及其数学思想进行总结。 几何画板动画演示,再次给学生以启发,容易让学生得到结论。
云端补救布置作业(44′36″—44′59″) 1、登录“家校帮”,观看课堂实录和微课,进行复习,完成推送的思考题和检测题.2、完成学案上的练习.3、选做题(1)如图,正方形ABCD中,∠MAN=45°,∠MAN的两边分别交BD于点M,N.求证: . (2)如图,在Rt△ABD中,∠BAD=90°,AB=AD,点M、N均在边BD上,且∠MAN=45°.求证: 学生课后登录“家校帮”,可以看到这节课的课堂实录,同时可以继续观看微课,根据自身情况,不断复习基本模型,并完成家校帮推送的课后检测习题,并完成学案。 使用“教学助手”推送本堂课的课堂实录、微课、思考题、检测题,学生可以登录“家校帮”,根据自身情况,不断观看课堂实录和微课,不断复习基本模型。同时,教师可以通过习题的完成情况,了解学情,为后续的教学提供依据。
教学流程图
【课堂实录】
1、环节:推送导学·自主学习
2、环节:复习旧知·检测反馈
(1)复习旧知
师:最近我们学习了旋转有关的概念,在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。这个定点称为什么?
生:旋转中心
师:转动的角称为什么?
生:旋转角
师:转动的方向称为什么?
生:旋转方向
师:旋转方向有几类?
生:两类,顺时针、逆时针
师:很好,这就是我们经常强调的旋转的三要素:旋转中心、旋转角、旋转方向。(板书)
师:此外,我们还学习了旋转的基本性质,大家观察这个图,将△ABC绕点O顺时针旋转一定的角度得到△,请问,在这个变换中,有什么结论呢?
生:
师:用文字怎么描述呢?
生:对应点到旋转中心的距离相等
师:很好,那么角度上有什么结论呢?
生:
师:用文字怎么描述呢?
生:对应点与旋转中心所连线段的夹角等于旋转角
师:很好,那么图形上有什么结论呢?
生:旋转前、后的图形全等。
师:很好,也就是哪两个图形全等?
生:△△
师:很好,既然有全等,那么我们就对应边相等、对应角相等。今天我们就继续学习旋转的应用。
(2)讲评课前导学
师:这是昨天“家校帮”导学单里的一道习题,老师看到88.2%的同学都回答正确了,但还是有一部分同学回答错误,现在请XX同学,你来回答一下,昨晚你选的是C,今天你能自我纠正一下吗?
生:不是旋转角
师:为什么不是呢?
生:因为点C与B不是对应点
师:那么C的对应点是哪个点?
生:点E
师:所以哪个角是旋转角?
生:
师:非常好,那么还有哪个角也是旋转角?
生:
检测反馈
师:这是两个等边三角形同一个顶点重合,其实就是我们很熟悉的手拉手模型,那么图中可以看作是旋转关系的是哪一对三角形呢?现在我们用随机抽人的方式完成这道题。(板书:等边三角形)
生:选C
师:很好,你能不能进一步告诉大家,此时的旋转角是多少度?
生:60°
师:为什么呢:
生:因为它是等边三角形
师:等边三角形与旋转角又有什么关系呢?
生:因为B与C是对应点,所以是旋转角,而它是60°
师:非常好,接着大家看这道题,这是两个等腰三角形同一个顶点重合,且顶角相等,请大家拿起
遥控器,做出选择。
(学生做出选择)
师:好的,大部分同学都选择正确了,大家告诉老师,这是为什么呀?
生:因为全等
师:哪一对全等?
生:△△
师:根据哪个判定?
生:SAS
师:很好,那么夹角是哪一对?
生:
师:很好,那么要注意用已知条件的角减去哪个角?
生:公共角
师:很好,接着,我们再看这道题目,两个直角三角形,同一个顶点重合,将△ADN绕点A顺时针旋转90°后,能与△ABE重合,如果AN=4,那么EN等于多少?现在,请同学们按下遥控器,进行抢答。
(某学生获得抢答权)
生:因为旋转,所以AE=AN=4,而,因此利用勾股定理,就得到
师:非常好。
环节:组织交流·释疑拓展
(1)组织交流
师:刚才我们的研究都是在三角形背景下,现在老师将这道题稍微做一些变化,延长EB、DN,相交于点C,这个时候的四边形ABCD就是一个什么图形?
生:正方形
师:很好,因为∠BAD=∠D=∠ABC=90°,而AB=AD,可以证明它是正方形。
现在,老师再添一条射线AM,使∠MAN=45°,于是,就在这个图形里出现了45°与90°,这就是我们今天要研究的半角模型,这其实是半角模型里非常特殊的一类,45°与90°。
那么,大家知道BM、MN、DN三者的数量关系是什么吗?
生:BM+DN=MN
师:很好,说明大家昨天有认真地预习这个微课视频,结论都记得,那么怎么证明呢?
生:将三角形ADN绕点A顺时针旋转90°,
师:很好,那么为什么你会选择这样的旋转呢?
生:因为我们有三条线段,这样做,可以让我们要它转化到两个两个三角形里面,然后利用它们对应边相等去证明。
师:很好,他其实已经想得很远了,这里涉及到三条线段,那么我们如果能够把这两条线段转移到一条直线上,就可以了,那么这样的旋转,这三点一定共线吗?
生:因为旋转,那两个对应角相等,所以这两个角相加等于180°
师:很好,因为旋转的辅助线经常涉及到三点共线,大家又经常忘记,所以我们以前常用什么辅助线添加方法?
生:截长补短
师:很好,准确说是截长补短中的补短,那么补短的目的是为了什么?
生:构造全等
师:那么如何证明全等呢?
生:SAS
师:然后呢?
生:因为这对全等,所以,∠1=∠2,∵∠BAD=90°,∠MAN=45°,
∴∠2+∠3=45°,∴∠1+∠3=45°,
师:很好,这是一个难点,接着证明哪个全等?
生:证明△≌△
师:很好,他已经把大概的方法说出来了,一开始用的是旋转的方法,那么一定要交代三点共线,为了避免这个问题,我们可以采取截长补短,关键是构造这两个三角形全等。现在请大家打开学案的第2页,完成第1题。
如图,在正方形ABCD中,∠MAN=45°,当∠MAN绕点A顺时针旋转到如图的位置时,它的两边分别交CB,DC于点M,N.线段BM,DN和MN之间有怎样的数量关系?写出猜想,并给予证明.
猜想:_________________________
证明:延长CB至点,使________,连接
∵四边形ABCD是正方形
∴AB=AD,∠ABC=∠D=90°∴
在△和△中,
∴△≌△(______),
∴,∠1=∠____,
∵∠BAD=90°,∠MAN=45°,
∴∠2+∠3=____°,∴∠1+∠3=____°,
∴,
在△和△中,
∴△≌△(______),∴,
又,
完成学案,教师点评
释疑拓展
师:刚才的这个方法是将红色的三角形进行旋转,那么还可以怎么旋转呢?
生:旋转绿色的三角形。
师:很好,准确地应该怎么说?
生:将△ABM绕点A逆时针旋转90°
师:那么用旋转又要涉及三点共线,我如果要避开旋转,应该怎么说?
生:延长CD至点,使=BM
师:很好,这个思路与刚才类似,现在请大家拿起遥控器,完成这道题。
学生选择,然后教师请选择正确的同学来解释。
师:请X号,你来告诉大家,为什么第1个结论是正确的?
生:因为可以证△≌△,就可以得到结论
师:很好,那么第2个结论为什么正确呢?
生:因为∠1=∠2,∠1+∠3=45°,所以∠2+∠3=45°,就可以证得第2个结论
师:很好,现在请X号来解释第3个结论
生:接下来,可以证明△≌△,就可以得到,等量代换,就可以得到第3个结论
师:非常好,刚才的两种辅助线都是在补短,那么本题可以截长吗?
生:可以
师:如果可以,应该怎么截?
生:在MN上截取ME=BM
师:可以构造全等吗?条件够吗?
生:不够
师:因此,请大家注意,截长补短因题而异
环节:变式教学·检测反馈
变式教学
师:现在,老师将这个图形再做变化,将∠MAN绕点A继续逆时针旋转,此时角的一边AM与CB的延长线相交,另一边与CB和DC的延长线都相交,我将与CB的交点命名为P,我用几何画板演示与P有关的线段,他们有数量关系吗?
生:没有
师:既然没有特别关系,那我们就不再研究了,我们依然研究BM、MN、DN的数量关系,现在请大家拿起刻度尺,测量一下这三条线段,它们有没有特殊的关系?
学生度量,并写出猜想。
生:BM+MN=DN
师:很好,老师还是先用几何画板看看是否成立。
几何画板初步验证结论
师:那么,应该如何证明呢?你能否从刚才得到结论?
生:旋转三角形ABM,绕点A逆时针旋转90°
师:很好,那么辅助线应该怎么写?
生:在DN上截取,
师:很好,现在请三四两组的同学完成这个证明。一二两组的同学,请思考,还能旋转哪个三角形,也能证明结论?
生:△ADN,绕点A顺时针旋转90°
师:很好,辅助线应该怎么写?
生:延长CB至点,使得
师:很好,请一二两组的同学,完成这个证明,这个问题有点难,请大家四人小组为单位,讨论一下,并写出你大概的证明思路。
(2)检测反馈
学生花5分钟讨论,并写出证明思路,教师请学生上台,阐述自己的证明思路:
方法一、
生:在DC上取点,使
师:很好,那么第一次是哪个全等?
生:
师:哪个判定?
生:SAS
师:那么这个全等可以得到什么结论?
生:∠1=∠2,
师:那么∠1+∠3=45°
生:所以∠2+∠3=45°,所以
师:很好,这个难点他突破了,接下来证哪个全等?
生:
师:很好,基本思路都对了,大家掌声鼓励。
方法二、
生:延长CB至点,使
师:证得哪对全等?
生:
师:用哪个判定?
生:SAS
师:由这个全等得到什么结论?
生:
师:接下来角度上有什么结论?
生:
师:而∠DAN+∠BAN=90°
生:所以,即
而∠MAN=45°,所以
师:很好,接下来证哪一对全等?
生:
师:很好,基本思路都对了,大家掌声鼓励。
刚才的图形是将这个45°的角绕点A顺时针旋转,如果老师将其逆时针旋转,能得到类似的结论吗?这道题作为课后的思考题,老师用“家校帮”推送给大家,请大家课后完成。
环节:归纳总结·拓展提升
拓展提升
师:刚才所有的研究都是在正方形的背景之下,那么对于矩形和菱形,等我们学习完相似后,再进行研究。现在我们来看这个更加一般的图形,没有了45°与90°,但是依然有半角关系,你能否给这个四边形增加条件,使得BM+MN=DN这个结论依然成立?能否由刚才的旋转得到启发?
生:AB=AD
师:很好,这个条件对于四边形而言,可以描述为什么?
生:邻边相等
师:很好,那么角度上有没有要求呢?
生:∠B+∠D=180°
师:用文字语言怎么描述?
生:对角互补
师:因此,我们得到半角模型的三个条件:半角、邻边相等、对角互补,只要具备了这些条件,我们就能用上今天的方法。
归纳总结
师:当我们从原来对正方形的研究上升到对一般四边形的研究,这体现了什么数学思想?
生:从特殊到一般
师:很好,那么在解题中,我们利用旋转,构造全等,把不熟悉的问题转化为熟悉的问题,这又体
现了什么数学思想?
生:转化思想
环节:云端补救·布置作业
(1)登录“家校帮”,观看课堂实录和微课,进行复习,完成推送的思考题和检测题.
(2)完成学案上的练习.
【教学反思】
基于智慧课堂的初中数学高效教学的实践研究
在移动互联网时代,“智慧课堂”是以建构主义学习理论为依据,利用大数据分析、教育云端、物联网等新一代信息技术打造的智能、高效的课堂,而《新课标》指出数学教学活动应激发学生兴趣,调动学生积极性,引发学生的数学思考,鼓励学生的创造性思维,在本堂课的教学中,我将智慧课堂与初中数学教学相结合,应用“336教学模式”,以学生为中心,以学定教,具体流程如下:
本堂课主要围绕“半角模型的应用”展开旋转复习,复习课是所有课型里比较难上的一种,所以在教学设计上,我主要采取变式教学,由易到难,从特殊到一般,让学生层层深入,体会旋转这一重要方法的运用,教学中也不断渗透从特殊到一般、转化等数学思想,同时,在课堂的组织教学中,也通过抢答、分组讨论、几何画板演示、学生讲题等多种形式调动学生的积极性,增强学生的自我探究能力。在教学模式上,围绕着“基于智慧课堂的初中数学高效教学的实践研究”这一课题,积极探索以学定教、提高课堂效率的方式,采用了“336教学模式”,将智慧课堂的课前推送、课中即时反馈,课后云端补救和检测等融入到授课环节中。
课前,我通过网络空间的教学助手推送导学单,让学生事先观看微课并完成检测,能让教师在授课前就较全面地了解学情,以学定教。课中,通过动手操作、分组讨论,引导学生利用旋转,构造全等,几何画板的动画演示,让学生直观感受了旋转在此类题型中的重要作用,有效突出了重点,突破了难点。此外,HITEACH TBL2的IRS即时反馈系统、抢答和互动课堂“移动讲台”的拍照功能,都能让我在授课中及时了解学情,以便迅速调整教学策略。课后,我通过教学助手推送“课堂实录”、微课、课堂思考题、课后检测习题,并让学生登录家校帮,根据自身情况及时观看课堂实录和微课,不断复习并检测,也能让教师及时了解到学生的学习效果,从而为后续的教学制定教学策略,实现以学定教的目的。
整堂课的教学中,我应用“336教学模式”,将信息技术与初中数学教学恰倒好处地结合,无论是课前推送的导学单、课中的即时反馈,还是课后的云端补救和检测等,都是以学生为中心,及时根据学情制定和调整教学策略,以学定教,实现了智慧课堂与初中数学教学的融合,从而提高了教学的有效性和针对性,促进了数学高效课堂的形成。
【点评】
翁希凡老师的这节课教学目标明确具体,知识目标达成很清晰,教师的教态自然大方、语言规范准确,讲解到位,采用“336教学模式”,以学定教,以学生为主体,重视学生学习方法的培养,重视探究能力的培养,重视逻辑思维的发展,题型设置从易到难,采用变式教学循序渐进,根据教学内容和学生实际恰当地选择教学手段和教学媒体,将网络空间、智慧教室、几何画板等信息化工具,有机结合,融入到数学课堂中,学生能积极主动参与各环节,参与度高,课堂衔接流畅,教学效果良好。
课前让学生观看微课、完成习题,有助于培养学生的自主学习能力,也可以让教师提前了解学情,以学定教。在课中对“课前预习”的习题讲评,让学生的预习效果得到进一步巩固和提升。同时,授课教师采用动手操作、分组讨论、学生讲题等教学形式,培养了学生的自主探究能力,教师注重对学生的引导,善于激发学生的学习热情。几何画板的动画演示,突出了重点,突破了难点。随机抽人、IRS即时反馈、抢答、互动课堂的拍照展示等,都很好地展示了学生的学习情况,教师能根据学情及时调整教学策略,面向全体学生反馈信息。在习题设置中,采取变式教学,层层递进,渗透了从特殊到一般、转化等数学思想,有利于学生养成良好的逻辑思维习惯。课后的及时推送,可以让学生观看到课堂实录等,让学生根据自身情况进行复习,课后的检测也可以让教师及时了解到学生的掌握情况,从而有的放矢地进行下节课的教学。
翁希凡老师的这节课主要是围绕“半角模型的应用”进行旋转复习,教师能根据教学目标,采用“336教学模式”,从学生学情出发,熟练地运用信息技术,以学定教,整个教学过程井然有序,实现了智慧课堂与初中数学教学的融合,提高了课堂教学的高效性,教学效果良好。
点评:叶蓉
第4题图
第3题图
第5题图
第1题图
第2题图
半角
模型
第1题图
PAGE
——半角模型的应用
人民教育出版社 初中数学 九年级上册 第二十三章
教材分析 “旋转变换”是初中图形变换中的一个重要内容,本节课是在学生学完了第二十三章《旋转》后的复习课,旨在帮助学生进一步理解旋转的概念和性质,并能用旋转变换深入理解“半角模型”。
学情分析 学生已经学移变换、轴对称变换、旋转变换这三个重要的图形变换,对几何图形已经具备了一定的认识,但是还缺乏一定的动态认识,对于在复杂图形中利用旋转变换解决问题,还存在一定难度。
教学目标 知识与技能 复习旋转的概念与性质;掌握利用旋转,构造全等的解题思路。
过程与方法 1、在问题的探讨中,通过一题多解,培养分析问题,多角度看待问题的能力;2、借助智慧课堂(网络空间的“教学助手”“互动课堂”“家校帮”、Hiteach软件、几何画板)等信息技术的使用,提高教与学的有效性、高效性。
情感、态度与价值观 在分组讨论、合作交流中,培养学生善于观察、勇于探索和勤于思考、合作交流的能力;体会从特殊到一般、转化等数学思想。
教学重点 复习旋转的概念与性质 简述解决重、难点的措施 课前推送微课和习题,让学生复习旋转的概念与性质,并完成自我检测,课堂复习环节,进一步通过检测形式,让学生继续复习旋转的概念与性质,突出重点。
教学难点 掌握利用旋转,构造全等的解题思路。 借助几何画板演示旋转动画,让学生直观感受旋转变换,突破难点,通过HITEACH的即时反馈、网络空间的拍照展示等功能,及时了解学情,进一步突破难点。
教学环境 云端一体互动课堂(“教学助手”课前推送导学单、“互动课堂”进行授课、“教学助手”课后推送课堂实录、思考题、课后检测题,学生登录“家校帮”观看微课、完成课前导学和课后思考题及检测。) 教学方法 自主合作探究与启发引导相结合
教学过程
教学环节 教师活动 学生活动 媒体作用及分析
推送导学自主学习(前一天晚上+课前)(0′06″—0′27″) 课前推送导学单(微课、课前检测题),提前了解学情,以学定教。 通过观看微课,复习旋转的概念与性质,并且初步认识半角模型的解题思路,完成习题,进行自我检测。 通过网络空间的“教学助手”推送导学单(微课、课前检测题),提前了解学情,以调整教学策略,实现以学定教的目的。
复习旧知检测反馈(0′28″—10′16″) 复习旋转概念与性质讲评课前导学情况;如图,△ABC和△ADE均为正三角形,则图中可看作是旋转关系的三角形是( ).△ABC和△ADE B.△ABC和△ABD C.△ABD和△ACE D.△ACE和△ADE4、如图,△ABC和△ADE都是等腰三角形,AB=AC,AD=AE,且∠DAE= ∠BAC,若∠DBA=25°,则∠ECA=( ).A.30° B.25° C.20° D.5°5、如图,△ADN是直角三角形,将△ADN绕点A顺时针旋转90°后,能与△ABE重合,如果AN=4,那么EN=______. 根据图形,复习旋转的概念和性质。让学生进行自我纠正。使用互动课堂的随机挑人功能,检测基本知识点的掌握情况。用HITEACH TBL2的IRS即时反馈,检测学生的知识运用情况。5、使用抢答功能,进一步巩固旧知。 让学生对导学单里的题目进行自我纠正,进一步加深学生对旋转概念、性质的理解;互动课堂的随机挑人,可以保证所有学生都有机会被抽到,能较客观地反映学生对基础知识的掌握情况;IRS即时反馈,能及时检测学生的知识运用情况,便于教师及时调整教学策略;使用抢答功能,进一步巩固旧知的同时,也能激发学生的学习兴趣。
组织交流释疑拓展(10′17″—24′34″) 1、如图,在正方形ABCD 中,∠MAN=45°,当 ∠MAN绕点A顺时针 旋转到如图的位置时,它的 的两边分别交CB,DC于点 M,N.线段BM,DN和M DN之间有怎样的数量关 关系?写出猜想,并给 予证明.几何画板演示旋转动画,并提示学生是否有其他做法?2、将第二种证法设置成选择题,及时检测学生对
“半角模型”解题方法的理解程度。如图,正方形ABCD中,∠MAN=45°,∠MAN的两边分别交BD于点M,N.延长CD至点,使,连接,下列结论:① ②③BM+DN=MN ④AN=AM,其中正确的是:( ).A.①② B.②④ C.①②③ D.①④3、提问:可以截长吗?阶段小结:解题思路:利用旋转,构造全等。 学生阐述解题思路,并完成学案;而后展示学案,教师点评,学生订正。在教师的启发和几何画板的动画演示下,类比第一种方法,迅速找到第二种方法。用IRS即时反馈系统,做出选择。 1、互动课堂的“移动讲台”功能,及时拍照,展示学生的学案。2、几何画板的动画演示,直观形象,较好地突出了重点,突破了难点。3、IRS即时反馈系统,一题多解,通过将第二种证法设置成选择形式,以便及时检测学生对“半角模型”解题方法的理解程度。
变式教学检测反馈(24′35″—41′37″) (变式1)如图,正方形ABCD中,∠MAN=45°,当∠MAN绕点A顺时针旋转到如图的位置时,它的两边分别交CB,DC的延长线于点M,N.线段BM,DN和MN之间有怎样的数量关系?写出猜想,并给予证明.引导学生动手测量(测量前,几何画板演示AN与BC的交点的情况),得到猜想,接着类比前两种方法进行解题,同时用几何画板演示动画演示突破难点。2、(变式2·课后思考)如图,正方形ABCD中,∠MAN=45°,当∠MAN绕点A逆时针旋转到如图的位置时,它的两边分别交CB,DC的反向延长线于点M,N.线段BM,DN和MN之间有怎样的数量关系?写出猜想,并给予证明. 第一、二两组的同学采用第一种方法进行证明;四两组的同学采用第二种方法进行证明。四人讨论,学生上台讲题,培养学生合作交流、自主探究的能力。学生在课后完成这道思考题。 用几何画板演示图形的变化过程,进行变式教学,让整堂复习课脉络清晰。互动课堂的“移动讲台”功能,及时将学生的解题思路拍照上传,学生上台利用互动课堂进行白板放大和书写,方便清晰,效果很好。利用家校帮推送这道思考题,及时有效。
归纳总结拓展提升(41′38″—44′35″) 1、如图,在四边形ABCD中,,要使BM+DN=MN,还需要增加哪些条件?引导学生总结半角模型的重要条件、解题思路、本节课所涉及的数学思想(从特殊到一般、转化思想)。 学生在前两题的启发下,利用旋转,得到半角模型的条件:半角、邻边相等、对角互补。在教师的启发引导下,学生对本堂课及其数学思想进行总结。 几何画板动画演示,再次给学生以启发,容易让学生得到结论。
云端补救布置作业(44′36″—44′59″) 1、登录“家校帮”,观看课堂实录和微课,进行复习,完成推送的思考题和检测题.2、完成学案上的练习.3、选做题(1)如图,正方形ABCD中,∠MAN=45°,∠MAN的两边分别交BD于点M,N.求证: . (2)如图,在Rt△ABD中,∠BAD=90°,AB=AD,点M、N均在边BD上,且∠MAN=45°.求证: 学生课后登录“家校帮”,可以看到这节课的课堂实录,同时可以继续观看微课,根据自身情况,不断复习基本模型,并完成家校帮推送的课后检测习题,并完成学案。 使用“教学助手”推送本堂课的课堂实录、微课、思考题、检测题,学生可以登录“家校帮”,根据自身情况,不断观看课堂实录和微课,不断复习基本模型。同时,教师可以通过习题的完成情况,了解学情,为后续的教学提供依据。
教学流程图
【课堂实录】
1、环节:推送导学·自主学习
2、环节:复习旧知·检测反馈
(1)复习旧知
师:最近我们学习了旋转有关的概念,在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。这个定点称为什么?
生:旋转中心
师:转动的角称为什么?
生:旋转角
师:转动的方向称为什么?
生:旋转方向
师:旋转方向有几类?
生:两类,顺时针、逆时针
师:很好,这就是我们经常强调的旋转的三要素:旋转中心、旋转角、旋转方向。(板书)
师:此外,我们还学习了旋转的基本性质,大家观察这个图,将△ABC绕点O顺时针旋转一定的角度得到△,请问,在这个变换中,有什么结论呢?
生:
师:用文字怎么描述呢?
生:对应点到旋转中心的距离相等
师:很好,那么角度上有什么结论呢?
生:
师:用文字怎么描述呢?
生:对应点与旋转中心所连线段的夹角等于旋转角
师:很好,那么图形上有什么结论呢?
生:旋转前、后的图形全等。
师:很好,也就是哪两个图形全等?
生:△△
师:很好,既然有全等,那么我们就对应边相等、对应角相等。今天我们就继续学习旋转的应用。
(2)讲评课前导学
师:这是昨天“家校帮”导学单里的一道习题,老师看到88.2%的同学都回答正确了,但还是有一部分同学回答错误,现在请XX同学,你来回答一下,昨晚你选的是C,今天你能自我纠正一下吗?
生:不是旋转角
师:为什么不是呢?
生:因为点C与B不是对应点
师:那么C的对应点是哪个点?
生:点E
师:所以哪个角是旋转角?
生:
师:非常好,那么还有哪个角也是旋转角?
生:
检测反馈
师:这是两个等边三角形同一个顶点重合,其实就是我们很熟悉的手拉手模型,那么图中可以看作是旋转关系的是哪一对三角形呢?现在我们用随机抽人的方式完成这道题。(板书:等边三角形)
生:选C
师:很好,你能不能进一步告诉大家,此时的旋转角是多少度?
生:60°
师:为什么呢:
生:因为它是等边三角形
师:等边三角形与旋转角又有什么关系呢?
生:因为B与C是对应点,所以是旋转角,而它是60°
师:非常好,接着大家看这道题,这是两个等腰三角形同一个顶点重合,且顶角相等,请大家拿起
遥控器,做出选择。
(学生做出选择)
师:好的,大部分同学都选择正确了,大家告诉老师,这是为什么呀?
生:因为全等
师:哪一对全等?
生:△△
师:根据哪个判定?
生:SAS
师:很好,那么夹角是哪一对?
生:
师:很好,那么要注意用已知条件的角减去哪个角?
生:公共角
师:很好,接着,我们再看这道题目,两个直角三角形,同一个顶点重合,将△ADN绕点A顺时针旋转90°后,能与△ABE重合,如果AN=4,那么EN等于多少?现在,请同学们按下遥控器,进行抢答。
(某学生获得抢答权)
生:因为旋转,所以AE=AN=4,而,因此利用勾股定理,就得到
师:非常好。
环节:组织交流·释疑拓展
(1)组织交流
师:刚才我们的研究都是在三角形背景下,现在老师将这道题稍微做一些变化,延长EB、DN,相交于点C,这个时候的四边形ABCD就是一个什么图形?
生:正方形
师:很好,因为∠BAD=∠D=∠ABC=90°,而AB=AD,可以证明它是正方形。
现在,老师再添一条射线AM,使∠MAN=45°,于是,就在这个图形里出现了45°与90°,这就是我们今天要研究的半角模型,这其实是半角模型里非常特殊的一类,45°与90°。
那么,大家知道BM、MN、DN三者的数量关系是什么吗?
生:BM+DN=MN
师:很好,说明大家昨天有认真地预习这个微课视频,结论都记得,那么怎么证明呢?
生:将三角形ADN绕点A顺时针旋转90°,
师:很好,那么为什么你会选择这样的旋转呢?
生:因为我们有三条线段,这样做,可以让我们要它转化到两个两个三角形里面,然后利用它们对应边相等去证明。
师:很好,他其实已经想得很远了,这里涉及到三条线段,那么我们如果能够把这两条线段转移到一条直线上,就可以了,那么这样的旋转,这三点一定共线吗?
生:因为旋转,那两个对应角相等,所以这两个角相加等于180°
师:很好,因为旋转的辅助线经常涉及到三点共线,大家又经常忘记,所以我们以前常用什么辅助线添加方法?
生:截长补短
师:很好,准确说是截长补短中的补短,那么补短的目的是为了什么?
生:构造全等
师:那么如何证明全等呢?
生:SAS
师:然后呢?
生:因为这对全等,所以,∠1=∠2,∵∠BAD=90°,∠MAN=45°,
∴∠2+∠3=45°,∴∠1+∠3=45°,
师:很好,这是一个难点,接着证明哪个全等?
生:证明△≌△
师:很好,他已经把大概的方法说出来了,一开始用的是旋转的方法,那么一定要交代三点共线,为了避免这个问题,我们可以采取截长补短,关键是构造这两个三角形全等。现在请大家打开学案的第2页,完成第1题。
如图,在正方形ABCD中,∠MAN=45°,当∠MAN绕点A顺时针旋转到如图的位置时,它的两边分别交CB,DC于点M,N.线段BM,DN和MN之间有怎样的数量关系?写出猜想,并给予证明.
猜想:_________________________
证明:延长CB至点,使________,连接
∵四边形ABCD是正方形
∴AB=AD,∠ABC=∠D=90°∴
在△和△中,
∴△≌△(______),
∴,∠1=∠____,
∵∠BAD=90°,∠MAN=45°,
∴∠2+∠3=____°,∴∠1+∠3=____°,
∴,
在△和△中,
∴△≌△(______),∴,
又,
完成学案,教师点评
释疑拓展
师:刚才的这个方法是将红色的三角形进行旋转,那么还可以怎么旋转呢?
生:旋转绿色的三角形。
师:很好,准确地应该怎么说?
生:将△ABM绕点A逆时针旋转90°
师:那么用旋转又要涉及三点共线,我如果要避开旋转,应该怎么说?
生:延长CD至点,使=BM
师:很好,这个思路与刚才类似,现在请大家拿起遥控器,完成这道题。
学生选择,然后教师请选择正确的同学来解释。
师:请X号,你来告诉大家,为什么第1个结论是正确的?
生:因为可以证△≌△,就可以得到结论
师:很好,那么第2个结论为什么正确呢?
生:因为∠1=∠2,∠1+∠3=45°,所以∠2+∠3=45°,就可以证得第2个结论
师:很好,现在请X号来解释第3个结论
生:接下来,可以证明△≌△,就可以得到,等量代换,就可以得到第3个结论
师:非常好,刚才的两种辅助线都是在补短,那么本题可以截长吗?
生:可以
师:如果可以,应该怎么截?
生:在MN上截取ME=BM
师:可以构造全等吗?条件够吗?
生:不够
师:因此,请大家注意,截长补短因题而异
环节:变式教学·检测反馈
变式教学
师:现在,老师将这个图形再做变化,将∠MAN绕点A继续逆时针旋转,此时角的一边AM与CB的延长线相交,另一边与CB和DC的延长线都相交,我将与CB的交点命名为P,我用几何画板演示与P有关的线段,他们有数量关系吗?
生:没有
师:既然没有特别关系,那我们就不再研究了,我们依然研究BM、MN、DN的数量关系,现在请大家拿起刻度尺,测量一下这三条线段,它们有没有特殊的关系?
学生度量,并写出猜想。
生:BM+MN=DN
师:很好,老师还是先用几何画板看看是否成立。
几何画板初步验证结论
师:那么,应该如何证明呢?你能否从刚才得到结论?
生:旋转三角形ABM,绕点A逆时针旋转90°
师:很好,那么辅助线应该怎么写?
生:在DN上截取,
师:很好,现在请三四两组的同学完成这个证明。一二两组的同学,请思考,还能旋转哪个三角形,也能证明结论?
生:△ADN,绕点A顺时针旋转90°
师:很好,辅助线应该怎么写?
生:延长CB至点,使得
师:很好,请一二两组的同学,完成这个证明,这个问题有点难,请大家四人小组为单位,讨论一下,并写出你大概的证明思路。
(2)检测反馈
学生花5分钟讨论,并写出证明思路,教师请学生上台,阐述自己的证明思路:
方法一、
生:在DC上取点,使
师:很好,那么第一次是哪个全等?
生:
师:哪个判定?
生:SAS
师:那么这个全等可以得到什么结论?
生:∠1=∠2,
师:那么∠1+∠3=45°
生:所以∠2+∠3=45°,所以
师:很好,这个难点他突破了,接下来证哪个全等?
生:
师:很好,基本思路都对了,大家掌声鼓励。
方法二、
生:延长CB至点,使
师:证得哪对全等?
生:
师:用哪个判定?
生:SAS
师:由这个全等得到什么结论?
生:
师:接下来角度上有什么结论?
生:
师:而∠DAN+∠BAN=90°
生:所以,即
而∠MAN=45°,所以
师:很好,接下来证哪一对全等?
生:
师:很好,基本思路都对了,大家掌声鼓励。
刚才的图形是将这个45°的角绕点A顺时针旋转,如果老师将其逆时针旋转,能得到类似的结论吗?这道题作为课后的思考题,老师用“家校帮”推送给大家,请大家课后完成。
环节:归纳总结·拓展提升
拓展提升
师:刚才所有的研究都是在正方形的背景之下,那么对于矩形和菱形,等我们学习完相似后,再进行研究。现在我们来看这个更加一般的图形,没有了45°与90°,但是依然有半角关系,你能否给这个四边形增加条件,使得BM+MN=DN这个结论依然成立?能否由刚才的旋转得到启发?
生:AB=AD
师:很好,这个条件对于四边形而言,可以描述为什么?
生:邻边相等
师:很好,那么角度上有没有要求呢?
生:∠B+∠D=180°
师:用文字语言怎么描述?
生:对角互补
师:因此,我们得到半角模型的三个条件:半角、邻边相等、对角互补,只要具备了这些条件,我们就能用上今天的方法。
归纳总结
师:当我们从原来对正方形的研究上升到对一般四边形的研究,这体现了什么数学思想?
生:从特殊到一般
师:很好,那么在解题中,我们利用旋转,构造全等,把不熟悉的问题转化为熟悉的问题,这又体
现了什么数学思想?
生:转化思想
环节:云端补救·布置作业
(1)登录“家校帮”,观看课堂实录和微课,进行复习,完成推送的思考题和检测题.
(2)完成学案上的练习.
【教学反思】
基于智慧课堂的初中数学高效教学的实践研究
在移动互联网时代,“智慧课堂”是以建构主义学习理论为依据,利用大数据分析、教育云端、物联网等新一代信息技术打造的智能、高效的课堂,而《新课标》指出数学教学活动应激发学生兴趣,调动学生积极性,引发学生的数学思考,鼓励学生的创造性思维,在本堂课的教学中,我将智慧课堂与初中数学教学相结合,应用“336教学模式”,以学生为中心,以学定教,具体流程如下:
本堂课主要围绕“半角模型的应用”展开旋转复习,复习课是所有课型里比较难上的一种,所以在教学设计上,我主要采取变式教学,由易到难,从特殊到一般,让学生层层深入,体会旋转这一重要方法的运用,教学中也不断渗透从特殊到一般、转化等数学思想,同时,在课堂的组织教学中,也通过抢答、分组讨论、几何画板演示、学生讲题等多种形式调动学生的积极性,增强学生的自我探究能力。在教学模式上,围绕着“基于智慧课堂的初中数学高效教学的实践研究”这一课题,积极探索以学定教、提高课堂效率的方式,采用了“336教学模式”,将智慧课堂的课前推送、课中即时反馈,课后云端补救和检测等融入到授课环节中。
课前,我通过网络空间的教学助手推送导学单,让学生事先观看微课并完成检测,能让教师在授课前就较全面地了解学情,以学定教。课中,通过动手操作、分组讨论,引导学生利用旋转,构造全等,几何画板的动画演示,让学生直观感受了旋转在此类题型中的重要作用,有效突出了重点,突破了难点。此外,HITEACH TBL2的IRS即时反馈系统、抢答和互动课堂“移动讲台”的拍照功能,都能让我在授课中及时了解学情,以便迅速调整教学策略。课后,我通过教学助手推送“课堂实录”、微课、课堂思考题、课后检测习题,并让学生登录家校帮,根据自身情况及时观看课堂实录和微课,不断复习并检测,也能让教师及时了解到学生的学习效果,从而为后续的教学制定教学策略,实现以学定教的目的。
整堂课的教学中,我应用“336教学模式”,将信息技术与初中数学教学恰倒好处地结合,无论是课前推送的导学单、课中的即时反馈,还是课后的云端补救和检测等,都是以学生为中心,及时根据学情制定和调整教学策略,以学定教,实现了智慧课堂与初中数学教学的融合,从而提高了教学的有效性和针对性,促进了数学高效课堂的形成。
【点评】
翁希凡老师的这节课教学目标明确具体,知识目标达成很清晰,教师的教态自然大方、语言规范准确,讲解到位,采用“336教学模式”,以学定教,以学生为主体,重视学生学习方法的培养,重视探究能力的培养,重视逻辑思维的发展,题型设置从易到难,采用变式教学循序渐进,根据教学内容和学生实际恰当地选择教学手段和教学媒体,将网络空间、智慧教室、几何画板等信息化工具,有机结合,融入到数学课堂中,学生能积极主动参与各环节,参与度高,课堂衔接流畅,教学效果良好。
课前让学生观看微课、完成习题,有助于培养学生的自主学习能力,也可以让教师提前了解学情,以学定教。在课中对“课前预习”的习题讲评,让学生的预习效果得到进一步巩固和提升。同时,授课教师采用动手操作、分组讨论、学生讲题等教学形式,培养了学生的自主探究能力,教师注重对学生的引导,善于激发学生的学习热情。几何画板的动画演示,突出了重点,突破了难点。随机抽人、IRS即时反馈、抢答、互动课堂的拍照展示等,都很好地展示了学生的学习情况,教师能根据学情及时调整教学策略,面向全体学生反馈信息。在习题设置中,采取变式教学,层层递进,渗透了从特殊到一般、转化等数学思想,有利于学生养成良好的逻辑思维习惯。课后的及时推送,可以让学生观看到课堂实录等,让学生根据自身情况进行复习,课后的检测也可以让教师及时了解到学生的掌握情况,从而有的放矢地进行下节课的教学。
翁希凡老师的这节课主要是围绕“半角模型的应用”进行旋转复习,教师能根据教学目标,采用“336教学模式”,从学生学情出发,熟练地运用信息技术,以学定教,整个教学过程井然有序,实现了智慧课堂与初中数学教学的融合,提高了课堂教学的高效性,教学效果良好。
点评:叶蓉
第4题图
第3题图
第5题图
第1题图
第2题图
半角
模型
第1题图
PAGE
同课章节目录
