数学人教A版(2019)选择性必修第二册4.2.2等差数列的前n项和公式 课件(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册4.2.2等差数列的前n项和公式 课件(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 561.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 20:04:10 | ||
图片预览







文档简介
(共20张PPT)
4.2.2 等差数列的前 n 项和公式
第4章
高中数学人教A版选修第二册(新课标)
等差数列的前n项和公式的推导.
(一)教学内容
1.了解等差数列的前n项和公式的推导.
2.推导并掌握等差数列的前n项和公式,提升逻辑推理和数学运算素养.
(二)教学目标
重点:等差数列前n项和公式的推导.
难点:等差数列前n项和公式的推导.
(三)教学重、难点
古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数.他们研究过三角形数:1,3,6,10,15,…,如图所示,这个图案中有n层.
问题情境
问题1: 如果图中的石子有100层,那么第1层到第100层一共用了多少石子?
追问1:高斯采用的是什么算法?
追问2:高斯在求和过程中利用了数列1,2,…,n,…的什么性质?
追问3:高斯求和法的实质是什么?
1+2+3+4+……+97+98+99+100=?
问题情境
高斯算法的实质:通过配对凑成相同的数,变“多步求和”为“一步相乘”,即将“不同数的求和”归化为“相同数的求和”
等差数列的下标和性质
首尾配对法
问题2: 如果图中的石子有101层,那么第1层到第101层一共用了多少石子?
思路2.(拿出中间项,再首尾配对):
原式=(1+101)+(2+100)+ +(50+52)+51
思路1.(拿出末项,再首尾配对):
原式=(1+2+ +100)+101
思路3.(先凑成偶数项,再配对):
原式=(0+1+2+ +101)
思路4.(先凑成偶数项,再配对):
原式=(1+2+ +101+102)
问题情境
问题3: 如果图中的石子有n层,那么第1层到第n层一共用了多少石子?
新知探究
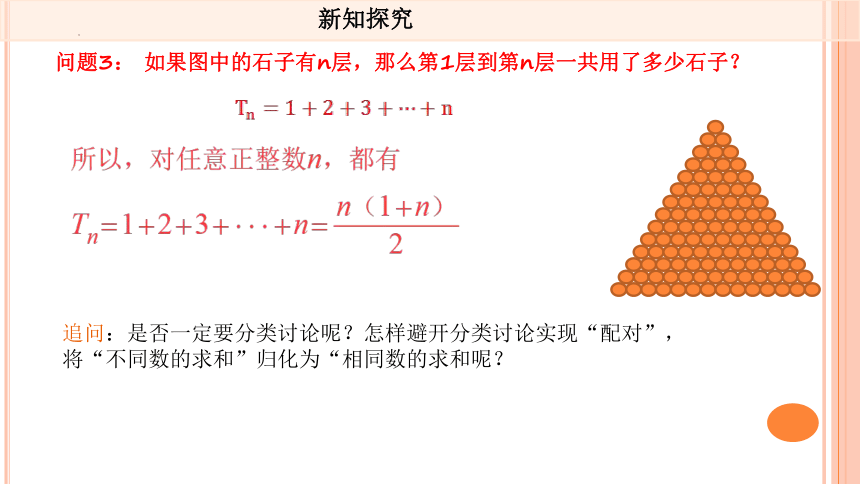
问题3: 如果图中的石子有n层,那么第1层到第n层一共用了多少石子?
新知探究
问题3: 如果图中的石子有n层,那么第1层到第n层一共用了多少石子?
追问:是否一定要分类讨论呢?怎样避开分类讨论实现“配对”,将“不同数的求和”归化为“相同数的求和呢?
新知探究
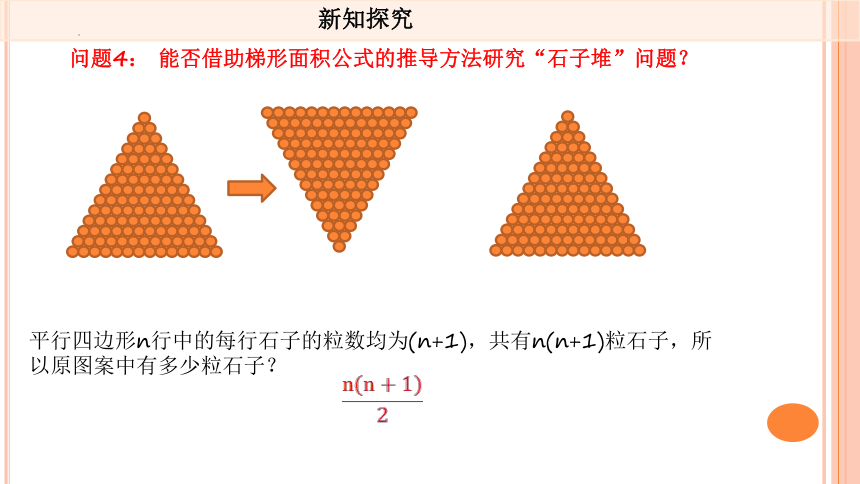
问题4: 能否借助梯形面积公式的推导方法研究“石子堆”问题?
平行四边形n行中的每行石子的粒数均为(n+1),共有n(n+1)粒石子,所以原图案中有多少粒石子?
新知探究
问题5: 你能用数学符号来表示图中的求解过程吗?
新知探究
问题6: 如何将这种“倒序相加法”推广到求公差为d的等差数列{an}的前n项和Sn呢?
新知探究
或者,利用通项公式an=a1+(n-1)d代入公式(1),可得公式(2)
Sn=a1+a2+…+an=a1+( a1+d)+…+[ a1+(n-1)d]=na1+[1+2+3+…+(n-1)]d
经过整理得到:
等差数列的前n项和公式
问题7: 根据前面的类比推导过程,你能说出等差数列{an}的前n项和公式与梯形的面积公式有什么联系吗?
追问:等差数列{an}的前n项和公式与一元二次函数有什么关系?
类比探究
a1
an
n
a1
a1
(n-1)d
n
等腰梯形的面积=平行四边形面积+三角形面积
追问:等差数列{an}的前n项和公式与一元二次函数有什么关系?
类比探究
(3)式是二次式.
课堂巩固
课堂巩固
课堂巩固
课堂巩固
例7: 已知一个等差数列{an}的前10项和是310,前20项和是1220,由这些条件能确定这个等差数列的首项和公差吗?
问题:请总结一下本节课的主要内容和思想方法.
课堂小结
布置作业
教科书第21页练习第1~4题
4.2.2 等差数列的前 n 项和公式
第4章
高中数学人教A版选修第二册(新课标)
等差数列的前n项和公式的推导.
(一)教学内容
1.了解等差数列的前n项和公式的推导.
2.推导并掌握等差数列的前n项和公式,提升逻辑推理和数学运算素养.
(二)教学目标
重点:等差数列前n项和公式的推导.
难点:等差数列前n项和公式的推导.
(三)教学重、难点
古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数.他们研究过三角形数:1,3,6,10,15,…,如图所示,这个图案中有n层.
问题情境
问题1: 如果图中的石子有100层,那么第1层到第100层一共用了多少石子?
追问1:高斯采用的是什么算法?
追问2:高斯在求和过程中利用了数列1,2,…,n,…的什么性质?
追问3:高斯求和法的实质是什么?
1+2+3+4+……+97+98+99+100=?
问题情境
高斯算法的实质:通过配对凑成相同的数,变“多步求和”为“一步相乘”,即将“不同数的求和”归化为“相同数的求和”
等差数列的下标和性质
首尾配对法
问题2: 如果图中的石子有101层,那么第1层到第101层一共用了多少石子?
思路2.(拿出中间项,再首尾配对):
原式=(1+101)+(2+100)+ +(50+52)+51
思路1.(拿出末项,再首尾配对):
原式=(1+2+ +100)+101
思路3.(先凑成偶数项,再配对):
原式=(0+1+2+ +101)
思路4.(先凑成偶数项,再配对):
原式=(1+2+ +101+102)
问题情境
问题3: 如果图中的石子有n层,那么第1层到第n层一共用了多少石子?
新知探究
问题3: 如果图中的石子有n层,那么第1层到第n层一共用了多少石子?
新知探究
问题3: 如果图中的石子有n层,那么第1层到第n层一共用了多少石子?
追问:是否一定要分类讨论呢?怎样避开分类讨论实现“配对”,将“不同数的求和”归化为“相同数的求和呢?
新知探究
问题4: 能否借助梯形面积公式的推导方法研究“石子堆”问题?
平行四边形n行中的每行石子的粒数均为(n+1),共有n(n+1)粒石子,所以原图案中有多少粒石子?
新知探究
问题5: 你能用数学符号来表示图中的求解过程吗?
新知探究
问题6: 如何将这种“倒序相加法”推广到求公差为d的等差数列{an}的前n项和Sn呢?
新知探究
或者,利用通项公式an=a1+(n-1)d代入公式(1),可得公式(2)
Sn=a1+a2+…+an=a1+( a1+d)+…+[ a1+(n-1)d]=na1+[1+2+3+…+(n-1)]d
经过整理得到:
等差数列的前n项和公式
问题7: 根据前面的类比推导过程,你能说出等差数列{an}的前n项和公式与梯形的面积公式有什么联系吗?
追问:等差数列{an}的前n项和公式与一元二次函数有什么关系?
类比探究
a1
an
n
a1
a1
(n-1)d
n
等腰梯形的面积=平行四边形面积+三角形面积
追问:等差数列{an}的前n项和公式与一元二次函数有什么关系?
类比探究
(3)式是二次式.
课堂巩固
课堂巩固
课堂巩固
课堂巩固
例7: 已知一个等差数列{an}的前10项和是310,前20项和是1220,由这些条件能确定这个等差数列的首项和公差吗?
问题:请总结一下本节课的主要内容和思想方法.
课堂小结
布置作业
教科书第21页练习第1~4题
