鲁教版九年级下册期中检测数学题(含答案)
文档属性
| 名称 | 鲁教版九年级下册期中检测数学题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期中检测题
(时间:120 分钟 满分:120分)
一、选择题(每题3分,共 30分)
1.若圆的半径为4cm,一个点和该圆的圆心的距离为6cm,则这个点和这个圆的位置关系是( )
A.点在圆上 B.点在圆外 C.点在圆内 D.点在圆内或点在圆外
2.如图,AB 是⊙O 的直径,C,D是⊙O 上两点,CD⊥AB,若∠DAB=65°,则∠BOC=( )
A.25° B.50° C.130° D.155°
3.如图,AB 是⊙O 的直径,CD 是⊙O 的弦,∠ABD=55°,则∠BCD的度数为( )
A.35° B.45° C.55° D.75°
4.如图,MN是半径为1 的⊙O 的直径,点 A 在⊙O 上,∠AMN=30°,B为 的中点,P 是直径MN 上一动点,则PA+PB 的最小值为( )
B. C.1 D.2
5.如图,已知AB 是⊙O 的直径,点 C 是 AB 延长线上一点,BC=OB,CE 是⊙O 的切线,切点为点 D,过点 A 作AE⊥CE,垂足为点 E,则CD:DE 的值是( )
A. B.1 C.2 D.3
6.半径为 R 的圆内接正四边形的周长为( )
A.2πR
7.用一个圆心角为120°、半径为2 的扇形作一个圆锥的侧面,则这个圆锥的底面圆的半径为( )
8.如图,直线 AB 与⊙O 相切于点A,弦CD∥AB,E,F 为圆上的两点,且∠CDE=∠ADF.若⊙O 的半径为 4,则弦 EF 的长为( )
A.4 C.5 D.6
9.如图,在扇形OAB中,已知∠AOB=90°,OA=过 的中点C 作CD⊥OA,CE⊥OB,垂足分别为D,E,则图中阴影部分的面积为( )
A.π-1
10.如图,正三角形ABC的边长为3,将△ABC绕它的外心O逆时针旋转 60°得到△A'B'C',则它们重叠部分的面积是( )
D.
二、填空题(每题3分,共24 分)
11.如图,在正十边形 A A A A A A A A A A 中,连接A A ,A A ,则
12.如图,在⊙O 中,四边形OABC 为菱形,点 D在 上,则∠ADC 的度数是_________.
13.已知圆锥的底面半径为1cm,高为 则它的侧面展开图的面积为__________cm .
14.如图所示,⊙O 是四边形ABCD的内切圆,E,F,G,H 是切点,点 P 是 上异于 E,H 的点,若 则∠EPH=___________.
15.如图,△ABC的三个顶点坐标分别为A(-1,3),B(-2,-2),C(4,- 2),则△ABC 外接圆半 径的 长 度为___________.
16.如图,量角器的直径与直角三角尺 ABC 的斜边AB 重合,其中量角器零度刻度线的端点 N 与点A 重合,射线CP从CA 处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第35 秒时,点 E 在量角器上对应的读数是_________度.
17.如图,⊙O 是△ABC 的外接圆, AD⊥BC 于点D,延长AD 交⊙O 于点E,若 BD=4,CD=1,则DE 的长是____________.
18.如图,在矩形 ABCD 中,BC=4,CD=2,以 AD 为直径的半圆O 与BC相切于点E,连接BD,则阴影部分的面积为____________.(结果保留π)
三、解答题(共66 分)
19.(10分)如图,在⊙O 中,直径 AB 与弦CD 相交于点 P,
(1)求的大小.
(2)已知 求圆心O到BD的距离.
20.(10 分)已知⊙O 的直径为 10,点 A,B,C 在⊙O 上,的平分线交⊙O于 点D.
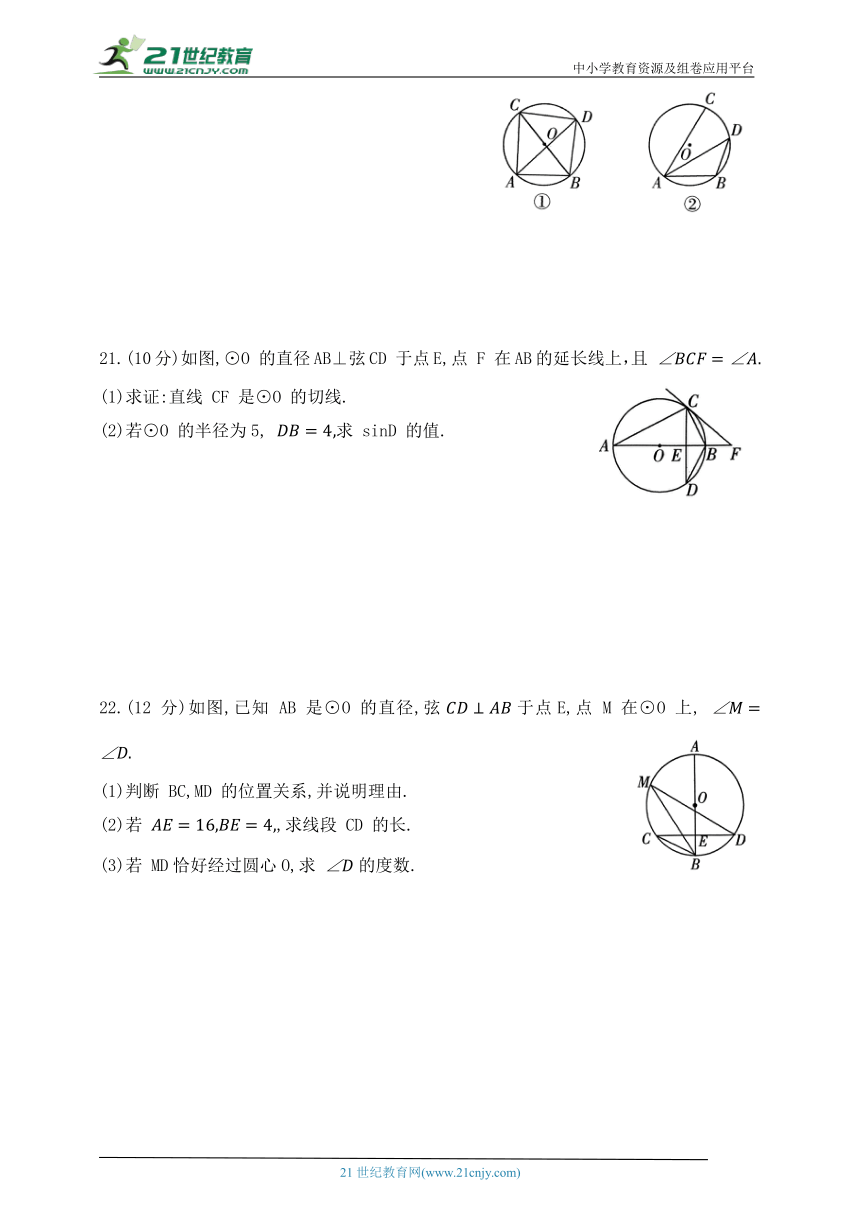
(1)如图①,若 BC 为⊙O 的直径, 求AC,BD,CD的长.
(2)如图②,若 求 BD的长.
21.(10分)如图,⊙O 的直径AB⊥弦CD 于点E,点 F 在AB的延长线上,且
(1)求证:直线 CF 是⊙O 的切线.
(2)若⊙O 的半径为5, 求 sinD 的值.
22.(12 分)如图,已知 AB 是⊙O 的直径,弦于点E,点 M 在⊙O 上,
(1)判断 BC,MD 的位置关系,并说明理由.
(2)若 ,求线段 CD 的长.
(3)若 MD恰好经过圆心O,求 的度数.
23.(12分)(扬州中考)如图,AB 是⊙O 的弦,过点O作OA,OC 交AB 于点P,
(1)求证:BC 是⊙O 的切线.
(2)已知 点 Q 是优弧AQB 上的一点.
①求 的度数.
②若 求优弧 AQB 的长.
24.(12分)(安徽中考)如图,AB 是半圆O的直径,C,D 是半圆O上不同于 A,B 的两点, AC 与 BD 相交于点F. BE 是半圆O所在圆的切线,与AC 的延长线相交于点 E.
(1)求证:
(2)若 求证:AC 平分
参考答案
1. B 2. C 3. A 4. B 5. C 6. C 7. D 8. B 9. B 10. C
11.54 12.60° 13.2π 14.65° 16.140 17. -5 18.π
19.解:(1)
(2)作( 于点E,则 DE又 即圆心O到BD 的距离为 3.
20.解:(1)由 BC 为⊙O 的直径,得 在中, 平分 BD.在Rt△BDC中,
(2)连接OB,OD.∵AD平分 ∠CAB,且∠CAB = 60°, ∴∠DAB= 又∵OB=OD,∴△OBD是等边三角形,∴BD=OB.∵⊙O的直径为10,∴OB=5,∴BD=5.
21.(1)证明:连接CO.∵AB 是直径,∴∠ACB=90°.∵OA= CO,∴∠A =∠OCA, ∴∠A+∠OCB =90°.又∵∠BCF=∠A,∴∠BCF+∠OCB=90°,∴直线CF是⊙O的切线. (2)解:∵⊙O的直径AB⊥弦CD 于点E,∴BC=BD.∵⊙O 的半径为5,DB=4,∴AB=10,
22.解:(1)BC∥MD.理由:∵∠M=∠D,∠M=∠C,∴∠D=∠C,∴BC∥MD.
(2)如图①,连接OC.∵AE=16,
在Rt△OCE 中,. 即 解得CE=8,∴CD=2CE=16.
(3)如图② 即∠BOD=2∠D.∵AB⊥CD,∴∠BOD+∠D=90°,即3∠D=90°,解得∠D=30°.
23.(1)证明:连接OB.∵OA=OB,∴∠OAB=∠OBA.∵PC=CB,∴∠CPB=∠PBC.∵∠APO=∠CPB,
∴∠APO=∠CBP.∵OC⊥OA,∴∠AOP = 90°,∴∠OAP+∠APO=90°,∴∠CBP +∠ABO=90°,
∴∠CBO=90°,∴BC 是⊙O 的切线.
(2)解:①∵∠BAO=25°,∴∠ABO=25°,∴∠AOB=1,②∵OA=18,∠AOB=130°,∴优弧 AQB 的长 =23π.
24.证明:(1)∵AB 是半圆O的直径,∴∠ACB=∠ADB=90°.
在 Rt△CBA 与 Rt△DAB 中, ∴Rt△CBA≌Rt△DAB(HL).
(2)∵BE=BF,∴∠E=∠BFE.∵BE 是半圆O所在圆的切线,∴∠ABE=90°,∴∠E+∠BAE=90°.由(1)知∠D=90°,∴∠DAF+∠AFD=90°.∵∠AFD=∠BFE,∴∠AFD=∠E.
∵∠DAF=90°-∠AFD,∠BAF=90°-∠E,∴∠DAF=∠BAF,∴AC平分∠DAB.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期中检测题
(时间:120 分钟 满分:120分)
一、选择题(每题3分,共 30分)
1.若圆的半径为4cm,一个点和该圆的圆心的距离为6cm,则这个点和这个圆的位置关系是( )
A.点在圆上 B.点在圆外 C.点在圆内 D.点在圆内或点在圆外
2.如图,AB 是⊙O 的直径,C,D是⊙O 上两点,CD⊥AB,若∠DAB=65°,则∠BOC=( )
A.25° B.50° C.130° D.155°
3.如图,AB 是⊙O 的直径,CD 是⊙O 的弦,∠ABD=55°,则∠BCD的度数为( )
A.35° B.45° C.55° D.75°
4.如图,MN是半径为1 的⊙O 的直径,点 A 在⊙O 上,∠AMN=30°,B为 的中点,P 是直径MN 上一动点,则PA+PB 的最小值为( )
B. C.1 D.2
5.如图,已知AB 是⊙O 的直径,点 C 是 AB 延长线上一点,BC=OB,CE 是⊙O 的切线,切点为点 D,过点 A 作AE⊥CE,垂足为点 E,则CD:DE 的值是( )
A. B.1 C.2 D.3
6.半径为 R 的圆内接正四边形的周长为( )
A.2πR
7.用一个圆心角为120°、半径为2 的扇形作一个圆锥的侧面,则这个圆锥的底面圆的半径为( )
8.如图,直线 AB 与⊙O 相切于点A,弦CD∥AB,E,F 为圆上的两点,且∠CDE=∠ADF.若⊙O 的半径为 4,则弦 EF 的长为( )
A.4 C.5 D.6
9.如图,在扇形OAB中,已知∠AOB=90°,OA=过 的中点C 作CD⊥OA,CE⊥OB,垂足分别为D,E,则图中阴影部分的面积为( )
A.π-1
10.如图,正三角形ABC的边长为3,将△ABC绕它的外心O逆时针旋转 60°得到△A'B'C',则它们重叠部分的面积是( )
D.
二、填空题(每题3分,共24 分)
11.如图,在正十边形 A A A A A A A A A A 中,连接A A ,A A ,则
12.如图,在⊙O 中,四边形OABC 为菱形,点 D在 上,则∠ADC 的度数是_________.
13.已知圆锥的底面半径为1cm,高为 则它的侧面展开图的面积为__________cm .
14.如图所示,⊙O 是四边形ABCD的内切圆,E,F,G,H 是切点,点 P 是 上异于 E,H 的点,若 则∠EPH=___________.
15.如图,△ABC的三个顶点坐标分别为A(-1,3),B(-2,-2),C(4,- 2),则△ABC 外接圆半 径的 长 度为___________.
16.如图,量角器的直径与直角三角尺 ABC 的斜边AB 重合,其中量角器零度刻度线的端点 N 与点A 重合,射线CP从CA 处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第35 秒时,点 E 在量角器上对应的读数是_________度.
17.如图,⊙O 是△ABC 的外接圆, AD⊥BC 于点D,延长AD 交⊙O 于点E,若 BD=4,CD=1,则DE 的长是____________.
18.如图,在矩形 ABCD 中,BC=4,CD=2,以 AD 为直径的半圆O 与BC相切于点E,连接BD,则阴影部分的面积为____________.(结果保留π)
三、解答题(共66 分)
19.(10分)如图,在⊙O 中,直径 AB 与弦CD 相交于点 P,
(1)求的大小.
(2)已知 求圆心O到BD的距离.
20.(10 分)已知⊙O 的直径为 10,点 A,B,C 在⊙O 上,的平分线交⊙O于 点D.
(1)如图①,若 BC 为⊙O 的直径, 求AC,BD,CD的长.
(2)如图②,若 求 BD的长.
21.(10分)如图,⊙O 的直径AB⊥弦CD 于点E,点 F 在AB的延长线上,且
(1)求证:直线 CF 是⊙O 的切线.
(2)若⊙O 的半径为5, 求 sinD 的值.
22.(12 分)如图,已知 AB 是⊙O 的直径,弦于点E,点 M 在⊙O 上,
(1)判断 BC,MD 的位置关系,并说明理由.
(2)若 ,求线段 CD 的长.
(3)若 MD恰好经过圆心O,求 的度数.
23.(12分)(扬州中考)如图,AB 是⊙O 的弦,过点O作OA,OC 交AB 于点P,
(1)求证:BC 是⊙O 的切线.
(2)已知 点 Q 是优弧AQB 上的一点.
①求 的度数.
②若 求优弧 AQB 的长.
24.(12分)(安徽中考)如图,AB 是半圆O的直径,C,D 是半圆O上不同于 A,B 的两点, AC 与 BD 相交于点F. BE 是半圆O所在圆的切线,与AC 的延长线相交于点 E.
(1)求证:
(2)若 求证:AC 平分
参考答案
1. B 2. C 3. A 4. B 5. C 6. C 7. D 8. B 9. B 10. C
11.54 12.60° 13.2π 14.65° 16.140 17. -5 18.π
19.解:(1)
(2)作( 于点E,则 DE又 即圆心O到BD 的距离为 3.
20.解:(1)由 BC 为⊙O 的直径,得 在中, 平分 BD.在Rt△BDC中,
(2)连接OB,OD.∵AD平分 ∠CAB,且∠CAB = 60°, ∴∠DAB= 又∵OB=OD,∴△OBD是等边三角形,∴BD=OB.∵⊙O的直径为10,∴OB=5,∴BD=5.
21.(1)证明:连接CO.∵AB 是直径,∴∠ACB=90°.∵OA= CO,∴∠A =∠OCA, ∴∠A+∠OCB =90°.又∵∠BCF=∠A,∴∠BCF+∠OCB=90°,∴直线CF是⊙O的切线. (2)解:∵⊙O的直径AB⊥弦CD 于点E,∴BC=BD.∵⊙O 的半径为5,DB=4,∴AB=10,
22.解:(1)BC∥MD.理由:∵∠M=∠D,∠M=∠C,∴∠D=∠C,∴BC∥MD.
(2)如图①,连接OC.∵AE=16,
在Rt△OCE 中,. 即 解得CE=8,∴CD=2CE=16.
(3)如图② 即∠BOD=2∠D.∵AB⊥CD,∴∠BOD+∠D=90°,即3∠D=90°,解得∠D=30°.
23.(1)证明:连接OB.∵OA=OB,∴∠OAB=∠OBA.∵PC=CB,∴∠CPB=∠PBC.∵∠APO=∠CPB,
∴∠APO=∠CBP.∵OC⊥OA,∴∠AOP = 90°,∴∠OAP+∠APO=90°,∴∠CBP +∠ABO=90°,
∴∠CBO=90°,∴BC 是⊙O 的切线.
(2)解:①∵∠BAO=25°,∴∠ABO=25°,∴∠AOB=1,②∵OA=18,∠AOB=130°,∴优弧 AQB 的长 =23π.
24.证明:(1)∵AB 是半圆O的直径,∴∠ACB=∠ADB=90°.
在 Rt△CBA 与 Rt△DAB 中, ∴Rt△CBA≌Rt△DAB(HL).
(2)∵BE=BF,∴∠E=∠BFE.∵BE 是半圆O所在圆的切线,∴∠ABE=90°,∴∠E+∠BAE=90°.由(1)知∠D=90°,∴∠DAF+∠AFD=90°.∵∠AFD=∠BFE,∴∠AFD=∠E.
∵∠DAF=90°-∠AFD,∠BAF=90°-∠E,∴∠DAF=∠BAF,∴AC平分∠DAB.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
