第五章 圆单元检测题(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
第五章检测题
(时间:90分钟 满分:120分)
一、选择题(每题3分,共30分)
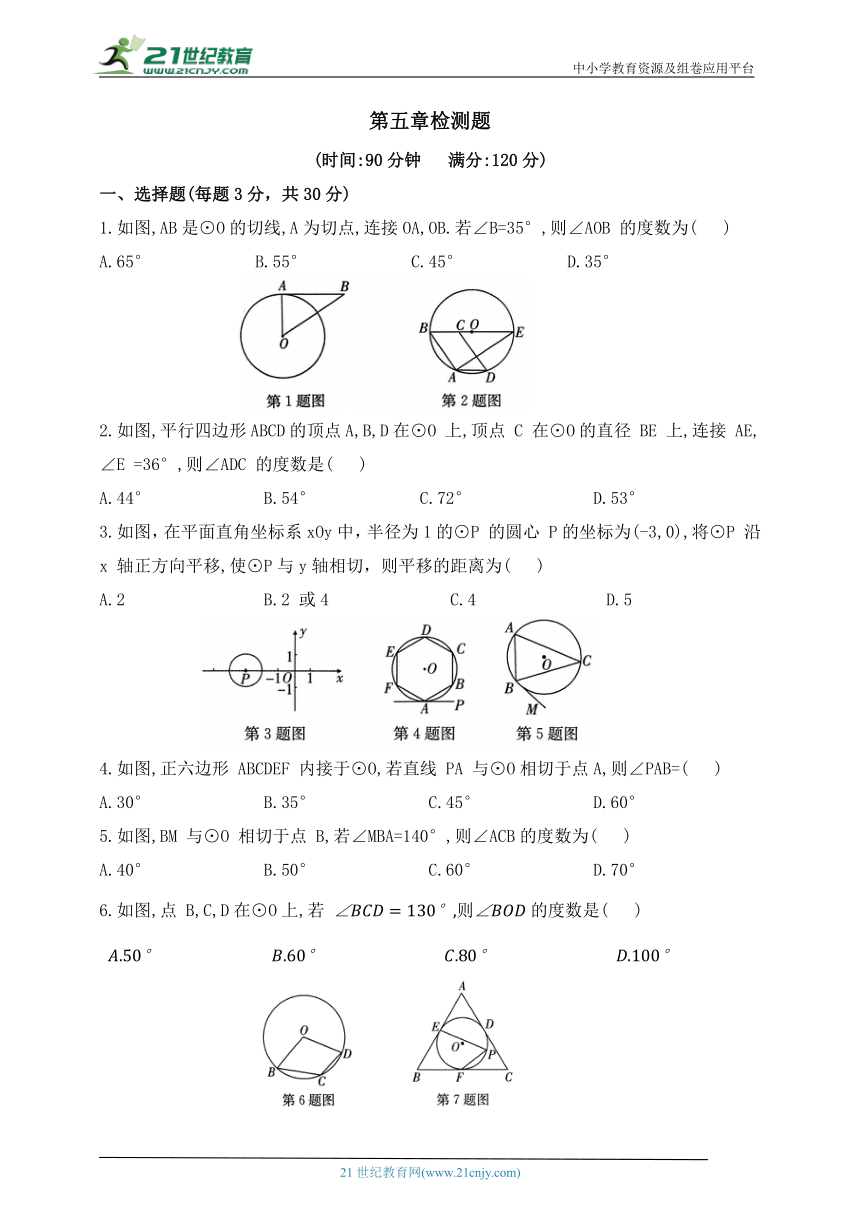
1.如图,AB是⊙O的切线,A为切点,连接OA,OB.若∠B=35°,则∠AOB 的度数为( )
A.65° B.55° C.45° D.35°
2.如图,平行四边形ABCD的顶点A,B,D在⊙O 上,顶点 C 在⊙O的直径 BE 上,连接 AE,∠E =36°,则∠ADC 的度数是( )
A.44° B.54° C.72° D.53°
3.如图,在平面直角坐标系xOy中,半径为1的⊙P 的圆心 P的坐标为(-3,0),将⊙P 沿x 轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
A.2 B.2 或4 C.4 D.5
4.如图,正六边形 ABCDEF 内接于⊙O,若直线 PA 与⊙O相切于点A,则∠PAB=( )
A.30° B.35° C.45° D.60°
5.如图,BM 与⊙O 相切于点 B,若∠MBA=140°,则∠ACB的度数为( )
A.40° B.50° C.60° D.70°
6.如图,点 B,C,D在⊙O上,若 则的度数是( )
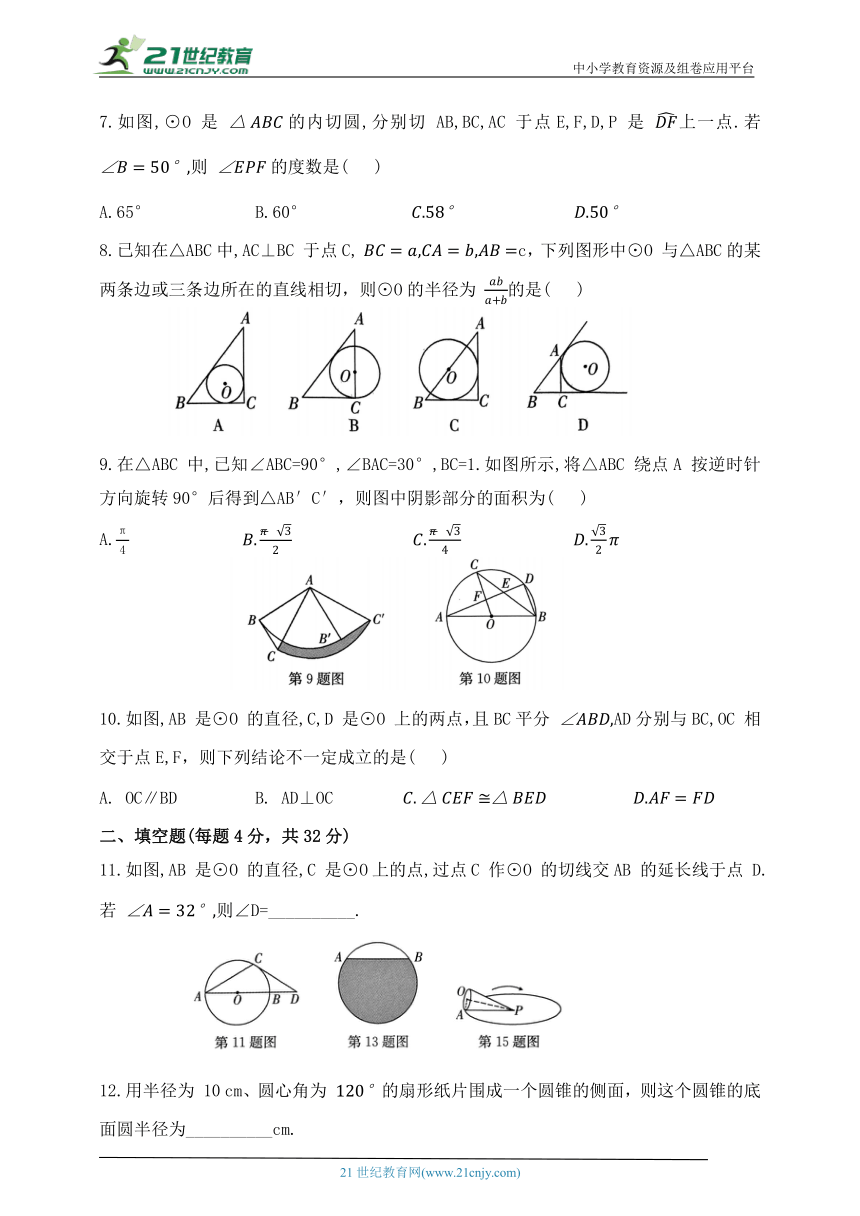
7.如图,⊙O 是 的内切圆,分别切 AB,BC,AC 于点E,F,D,P 是 上一点.若 则 的度数是( )
A.65° B.60°
8.已知在△ABC中,AC⊥BC 于点C, c,下列图形中⊙O 与△ABC的某两条边或三条边所在的直线相切,则⊙O的半径为 的是( )
9.在△ABC 中,已知∠ABC=90°,∠BAC=30°,BC=1.如图所示,将△ABC 绕点A 按逆时针方向旋转90°后得到△AB′C′,则图中阴影部分的面积为( )
A.
10.如图,AB 是⊙O 的直径,C,D 是⊙O 上的两点,且BC平分 AD分别与BC,OC 相交于点E,F,则下列结论不一定成立的是( )
A. OC∥BD B. AD⊥OC
二、填空题(每题4分,共32分)
11.如图,AB 是⊙O 的直径,C 是⊙O上的点,过点C 作⊙O 的切线交AB 的延长线于点 D.若 则∠D=__________.
12.用半径为 10 cm、圆心角为 的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为__________cm.
13.如图,水平放置的圆柱形排水管的截面直径是1m,其中水面的宽AB 为0.8m,则排水管内水的深度为__________m.
14.已知△ABC的三边a,b,c满足 ,则△ABC的外接圆半径是_____________.
15.如图,圆锥的底面圆心为O,半径OA=1,顶点为 P,将圆锥置于平面上,若保持顶点 P 位置不变,将圆锥顺时针滚动三周后点 A 恰好第一次回到原处,则圆锥的高OP=___________.
16.如图,以O为圆心的两个同心圆中,大圆的弦AB 与小圆相切于点C,若大圆的半径为 10cm,小圆的半径为 6cm,则弦AB 的长为__________cm.
17.如图,正方形ABCD 的边长为2,以BC 为直径的半圆O交对角线BD 于点E,则阴影部分的面积为_____________.(结果保留π)
18.如图,在扇形CAB 中,CD⊥AB,垂足为 D,⊙E 是△ACD 的内切圆,连接AE,BE,则∠AEB 的度数为_____________.
三、解答题(共 58分)
19.(10分) 如图,在⊙O 中,D,E 分别是半径OA,OB 的中点,点 C 在⊙O 上, 求证:
20.(12分)在⊙O 中,直径. BC 是弦, 点P 在BC 上,点Q 在⊙O 上,且
(1)如图①,当. ∥时,求P Q的 长.
(2)如图②,当点 P 在BC 上移动时,求 PQ 长的最大值.
21.(12分)如图,已知AB 是⊙O的直径,C,D 是⊙O 上的点,( 交AD于点E,连接BC.
(1)求证:
(2)若 求 的长.
22.(12 分)如图,已知⊙O 是等边三角形 ABC 的外接圆,点 D 在⊙O 上,在CD 的延长线上有一点 F,使DF=DA,AE∥BC交CF 于点E.
(1)求证:EA 是⊙O 的切线.
(2)求证:
23.(12分)如图,⊙O 的直径 弦AB 于点H,E 是 上一动点,连接AE 交 DF 于点G,连接FE 并延长交AB 的延长线于点C,
(1)求 FD 的长.
(2)在点 E 运动的过程中,EF·CF 的值是否为定值 若是,求出其定值;若不是,请说明理由.
(3)当点 E 运动到 的中点时,求 的面积.
参考答案
1. B 2. B 3. B 4. A 5. A 6. D
7. A [解析]连接OE,OF.∵⊙O是 的内切圆,E,F是切点,
8. C
9. B [解析]∵
10. C [解析]由圆周角定理的推论和角平分线得出∠ADB=90°,∠OBC=∠DBC,由等腰三角形的性质得出∠OCB=∠OBC,进一步得出∠DBC=∠OCB,证出OC∥BD,故选项 A成立;由平行线的性质得出AD⊥OC,故选项B成立;由垂径定理得出AF=FD,故选项D成立;△CEF 和△BED中,边的关系不确定,△CEF 与△BED不一定全等,故选项C不一定成立.
11.26° 12. 13.0.8 14. 15.2 16.16 18.135°
证明:∵D,E 分别是半径OA,OB 的中点,∴OD=OE.
在△ODC 与△OEC 中, (SSS),∴∠AOC=∠BOC,∴AC=CB.
20.解:(1)连接OQ.∵OP⊥PQ,PQ∥AB,∴OP⊥AB.
在Rt△OPB中,OP=OB·tan∠ABC=3tan30°= .
在Rt△OPQ中,
(2)连接OC 当OP 最小时,PQ最大,此时OP⊥BC,OP=OB·sin∠ABC=∴PQ长的最大值为
21.(1)证明:∵AB 是⊙O 的直径,∴∠ADB = 90°.
∵OC∥BD,∴∠AEO=∠ADB=90°,即 OC⊥AD,∴AE=ED.
(2)解: ∴∠ABC=∠CBD=36°,∴∠AOC=2∠ABC=2×36°
的长
22.证明:(1)连接OD,OA.∵⊙O 是等边三角形ABC 的外接圆,∴∠OAC =30°,∠BCA =60°. ∵AE∥BC,∴∠EAC=∠BCA=60°,∴∠OAE=∠OAC+∠EAC=30°+60°=90°,∴EA 是⊙O 的切线.
(2)∵△ABC是等边三角形,∴AB=AC,∠BAC=∠ABC=60°.∵A,B,C,D四点共圆,∴∠ADF=∠ABC=60°.∵DA=DF,∴△ADF 是等边三角形,∴AD=AF,∠DAF=60°,∴∠BAC+∠CAD=∠DAF+∠CAD,即∠BAD=∠CAF.
在△BAD 和△CAF 中, ∴△BAD≌△CAF,∴BD=CF.
23.解:(1)连接OA.∵直径 FD⊥弦 AB 于点 H,∴AH= 设 OA =x,在 Rt△OAH 中, 即
(2)EF·CF 的值是定值.∵直径 FD⊥弦 AB 于点 H,∴AF=BF,.∴∠BAF=∠AEF.
∵∠AFE=∠CFA,在
Rt△AFH 中, ·CF = 80.
(3)连 接 OE. ∵E 点 是 的 中点,∴∠FAE=45°,∠EOF =90°,∴∠EOH =∠AHG.
即
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章检测题
(时间:90分钟 满分:120分)
一、选择题(每题3分,共30分)
1.如图,AB是⊙O的切线,A为切点,连接OA,OB.若∠B=35°,则∠AOB 的度数为( )
A.65° B.55° C.45° D.35°
2.如图,平行四边形ABCD的顶点A,B,D在⊙O 上,顶点 C 在⊙O的直径 BE 上,连接 AE,∠E =36°,则∠ADC 的度数是( )
A.44° B.54° C.72° D.53°
3.如图,在平面直角坐标系xOy中,半径为1的⊙P 的圆心 P的坐标为(-3,0),将⊙P 沿x 轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
A.2 B.2 或4 C.4 D.5
4.如图,正六边形 ABCDEF 内接于⊙O,若直线 PA 与⊙O相切于点A,则∠PAB=( )
A.30° B.35° C.45° D.60°
5.如图,BM 与⊙O 相切于点 B,若∠MBA=140°,则∠ACB的度数为( )
A.40° B.50° C.60° D.70°
6.如图,点 B,C,D在⊙O上,若 则的度数是( )
7.如图,⊙O 是 的内切圆,分别切 AB,BC,AC 于点E,F,D,P 是 上一点.若 则 的度数是( )
A.65° B.60°
8.已知在△ABC中,AC⊥BC 于点C, c,下列图形中⊙O 与△ABC的某两条边或三条边所在的直线相切,则⊙O的半径为 的是( )
9.在△ABC 中,已知∠ABC=90°,∠BAC=30°,BC=1.如图所示,将△ABC 绕点A 按逆时针方向旋转90°后得到△AB′C′,则图中阴影部分的面积为( )
A.
10.如图,AB 是⊙O 的直径,C,D 是⊙O 上的两点,且BC平分 AD分别与BC,OC 相交于点E,F,则下列结论不一定成立的是( )
A. OC∥BD B. AD⊥OC
二、填空题(每题4分,共32分)
11.如图,AB 是⊙O 的直径,C 是⊙O上的点,过点C 作⊙O 的切线交AB 的延长线于点 D.若 则∠D=__________.
12.用半径为 10 cm、圆心角为 的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为__________cm.
13.如图,水平放置的圆柱形排水管的截面直径是1m,其中水面的宽AB 为0.8m,则排水管内水的深度为__________m.
14.已知△ABC的三边a,b,c满足 ,则△ABC的外接圆半径是_____________.
15.如图,圆锥的底面圆心为O,半径OA=1,顶点为 P,将圆锥置于平面上,若保持顶点 P 位置不变,将圆锥顺时针滚动三周后点 A 恰好第一次回到原处,则圆锥的高OP=___________.
16.如图,以O为圆心的两个同心圆中,大圆的弦AB 与小圆相切于点C,若大圆的半径为 10cm,小圆的半径为 6cm,则弦AB 的长为__________cm.
17.如图,正方形ABCD 的边长为2,以BC 为直径的半圆O交对角线BD 于点E,则阴影部分的面积为_____________.(结果保留π)
18.如图,在扇形CAB 中,CD⊥AB,垂足为 D,⊙E 是△ACD 的内切圆,连接AE,BE,则∠AEB 的度数为_____________.
三、解答题(共 58分)
19.(10分) 如图,在⊙O 中,D,E 分别是半径OA,OB 的中点,点 C 在⊙O 上, 求证:
20.(12分)在⊙O 中,直径. BC 是弦, 点P 在BC 上,点Q 在⊙O 上,且
(1)如图①,当. ∥时,求P Q的 长.
(2)如图②,当点 P 在BC 上移动时,求 PQ 长的最大值.
21.(12分)如图,已知AB 是⊙O的直径,C,D 是⊙O 上的点,( 交AD于点E,连接BC.
(1)求证:
(2)若 求 的长.
22.(12 分)如图,已知⊙O 是等边三角形 ABC 的外接圆,点 D 在⊙O 上,在CD 的延长线上有一点 F,使DF=DA,AE∥BC交CF 于点E.
(1)求证:EA 是⊙O 的切线.
(2)求证:
23.(12分)如图,⊙O 的直径 弦AB 于点H,E 是 上一动点,连接AE 交 DF 于点G,连接FE 并延长交AB 的延长线于点C,
(1)求 FD 的长.
(2)在点 E 运动的过程中,EF·CF 的值是否为定值 若是,求出其定值;若不是,请说明理由.
(3)当点 E 运动到 的中点时,求 的面积.
参考答案
1. B 2. B 3. B 4. A 5. A 6. D
7. A [解析]连接OE,OF.∵⊙O是 的内切圆,E,F是切点,
8. C
9. B [解析]∵
10. C [解析]由圆周角定理的推论和角平分线得出∠ADB=90°,∠OBC=∠DBC,由等腰三角形的性质得出∠OCB=∠OBC,进一步得出∠DBC=∠OCB,证出OC∥BD,故选项 A成立;由平行线的性质得出AD⊥OC,故选项B成立;由垂径定理得出AF=FD,故选项D成立;△CEF 和△BED中,边的关系不确定,△CEF 与△BED不一定全等,故选项C不一定成立.
11.26° 12. 13.0.8 14. 15.2 16.16 18.135°
证明:∵D,E 分别是半径OA,OB 的中点,∴OD=OE.
在△ODC 与△OEC 中, (SSS),∴∠AOC=∠BOC,∴AC=CB.
20.解:(1)连接OQ.∵OP⊥PQ,PQ∥AB,∴OP⊥AB.
在Rt△OPB中,OP=OB·tan∠ABC=3tan30°= .
在Rt△OPQ中,
(2)连接OC 当OP 最小时,PQ最大,此时OP⊥BC,OP=OB·sin∠ABC=∴PQ长的最大值为
21.(1)证明:∵AB 是⊙O 的直径,∴∠ADB = 90°.
∵OC∥BD,∴∠AEO=∠ADB=90°,即 OC⊥AD,∴AE=ED.
(2)解: ∴∠ABC=∠CBD=36°,∴∠AOC=2∠ABC=2×36°
的长
22.证明:(1)连接OD,OA.∵⊙O 是等边三角形ABC 的外接圆,∴∠OAC =30°,∠BCA =60°. ∵AE∥BC,∴∠EAC=∠BCA=60°,∴∠OAE=∠OAC+∠EAC=30°+60°=90°,∴EA 是⊙O 的切线.
(2)∵△ABC是等边三角形,∴AB=AC,∠BAC=∠ABC=60°.∵A,B,C,D四点共圆,∴∠ADF=∠ABC=60°.∵DA=DF,∴△ADF 是等边三角形,∴AD=AF,∠DAF=60°,∴∠BAC+∠CAD=∠DAF+∠CAD,即∠BAD=∠CAF.
在△BAD 和△CAF 中, ∴△BAD≌△CAF,∴BD=CF.
23.解:(1)连接OA.∵直径 FD⊥弦 AB 于点 H,∴AH= 设 OA =x,在 Rt△OAH 中, 即
(2)EF·CF 的值是定值.∵直径 FD⊥弦 AB 于点 H,∴AF=BF,.∴∠BAF=∠AEF.
∵∠AFE=∠CFA,在
Rt△AFH 中, ·CF = 80.
(3)连 接 OE. ∵E 点 是 的 中点,∴∠FAE=45°,∠EOF =90°,∴∠EOH =∠AHG.
即
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
