苏科版八年级数学下册试题 9.5三角形的中位线 同步练习 (含答案)
文档属性
| 名称 | 苏科版八年级数学下册试题 9.5三角形的中位线 同步练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 189.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-04 08:29:13 | ||
图片预览




文档简介
9.5三角形的中位线
一.选择题
1.顺次连结对角线互相垂直的四边形各边中点所构成的四边形一定是( )
A.矩形 B.菱形 C.正方形 D.不确定
2.△ABC中,AB=7,BC=6,AC=5,点D、E、F分别是三边的中点,则△DEF的周长为( )
A.4.5 B.9 C.10 D.12
3.已知等腰三角形的两条中位线的长分别为3和5,则此等腰三角形的周长为( )
A.22 B.26 C.22或26 D.13
4.如图,在△ABC中,D是AC的中点,且BD⊥AC,DE∥BC,交AB于点E,BC=7cm,AC=6cm,则△AED的周长等于( )
A.12cm B.10cm C.7cm D.9cm
5.四边形ABCD中,AB=1,CD=4,M、N分别是AD、BC的中点,则线段MN的取值范围是( )
A.3<MN<5 B.3<MN≤5 C.MN D.MN
6.如图,D、E分别为△ABC中AB、AC边上的中点,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
A.1 B. C.2 D.
7.如图,四边形ABCD中,∠A=90°,AB=2,AD=2,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A.3 B.2 C.4 D.2
8.如图,在四边形ABCD中,AB=6,BC=10,∠A=130°,∠D=100°,AD=CD.若点E,F分别是边AD,CD的中点,则EF的长是( )
A.3 B.4 C.2 D.
9.如图,依次连接任意四边形ABCD四条边的中点得到四边形EFGH,添加下列条件能判断四边形EFGH是菱形的是( )
A.AB=BC B.AB⊥BC C.AC⊥BD D.AC=BD
10.已知在四边形ABCD中,AB=3,CD=5,M,N分别是AD,BC的中点,则线段MN的取值范围是( )
A.1<MN<4 B.1<MN≤4 C.2<MN<8 D.2<MN≤8
11.如图,在Rt△ABC中,∠B=90°,BC=5,AB=12,点D,E分别是AB,AC的中点,CF平分Rt△ABC的一个外角∠ACM,交DE的延长线于点F,则DF的长为( )
A.5 B.8.5 C.9 D.12
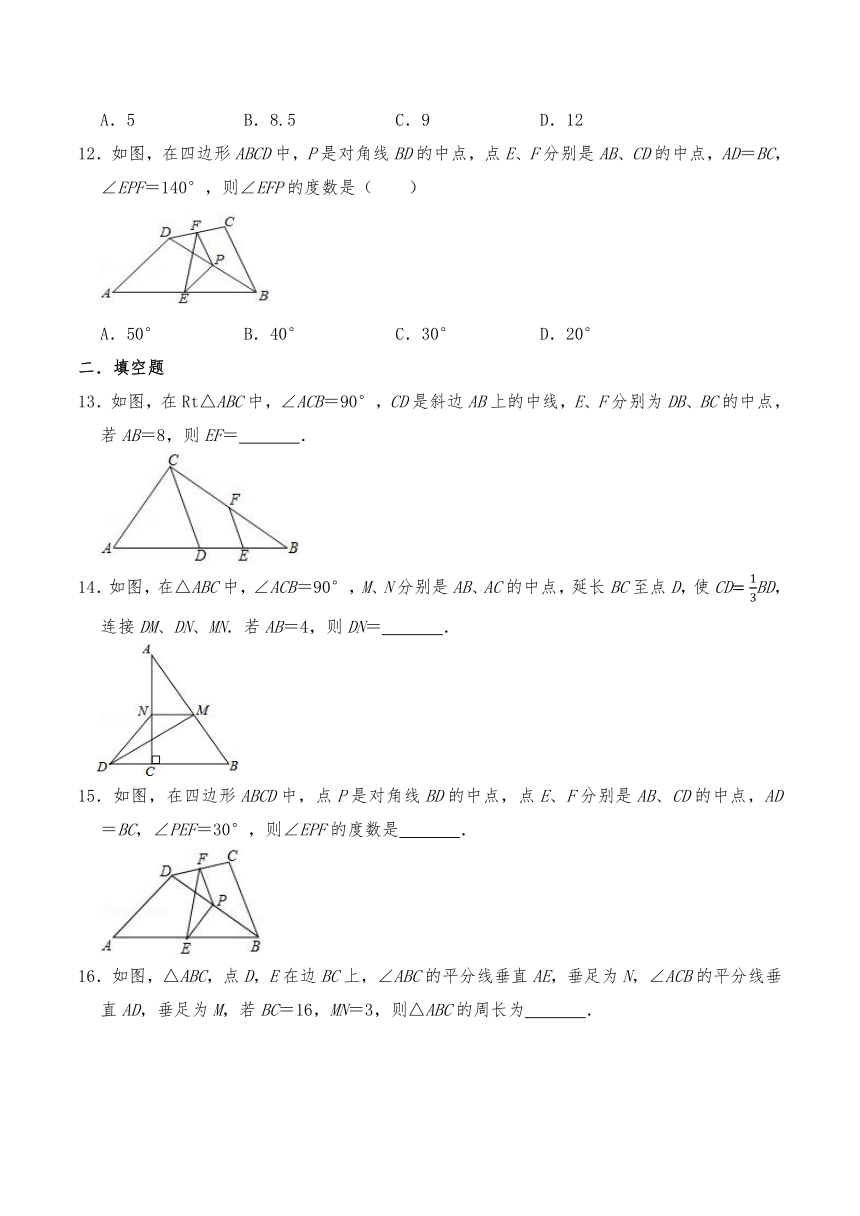
12.如图,在四边形ABCD中,P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠EPF=140°,则∠EFP的度数是( )
A.50° B.40° C.30° D.20°
二.填空题
13.如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,E、F分别为DB、BC的中点,若AB=8,则EF= .
14.如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CDBD,连接DM、DN、MN.若AB=4,则DN= .
15.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是 .
16.如图,△ABC,点D,E在边BC上,∠ABC的平分线垂直AE,垂足为N,∠ACB的平分线垂直AD,垂足为M,若BC=16,MN=3,则△ABC的周长为 .
17.如图,在四边形BCDE中,BC⊥CD,DE⊥CD,AB⊥AE,垂足分别为C,D,A,BC≠AC,点M,N,F分别为AB,AE,BE的中点,连接MN,MF,NF.当BC=4,DE=5,∠FMN=45°时,则BE的长为 .
18.如图,AD为△ABC中∠BAC的外角平分线,BD⊥AD于点D,E为BC中点,DE=4,AC=2,则AB长为 .
19.如图,Rt△ABC中,∠C=90°,BC=6,AC=10,D,E分别是AC和BC上的点,且CE=2,CD=4,连接BD,AE.G、H分别是AE和BD的中点,连接GH,则线段GH的长为 .
20.如图,△ABC中,AB=10,AC=7,AD平分∠BAC,AE是BC边上的中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为 .
三.解答题
21.如图,在等边△ABC中,D,E分别为AB,AC的中点,延长BC至点F,使CFBC,连结CD和EF.
(1)求证:CD=EF;
(2)猜想:△ABC的面积与四边形BDEF的面积的关系,并说明理由.
22.一个对角线相等的四边形ABCD,E、F分别为AB,CD的中点,EF分别交对角线BD,AC于M,N,求证:△OMN是等腰三角形.
23.如图,在四边形ABCD中,对角线AC=BD,E,F为AB、CD的中点,连接EF交BD、AC于P、Q,取BC中点G,连EG、FG,求证:OP=OQ.
24.如图,在四边形ABCD中,AB⊥BC,连接AC,E,F,M分别是AD,DC,AC的中点,连接EF,BM.求证:EF=BM.
25.如图,在△ABC中,AB=12cm,AC=8cm,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于点F,交AB于点G,连接EF,求线段EF的长.
26.如图,△ABC中,AH⊥BC于点H,点D,E分别是AB,AC的中点,连接DH,EH,DE.
(1)求证:AD=DH;
(2)若四边形ADHE的周长是30,△ADE的周长是21,求BC的长.
27.如图,已知AO是△ABC的∠A的平分线,BD⊥AO的延长线于D,E是BC的中点.
求证:DE(AB﹣AC)
28.已知:△ABC中,D是BC上的一点,E、F、G、H分别是BD、BC、AC、AD的中点,
求证:EG、HF互相平分.
29.△ABC的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证:EF∥DG,且EF=DG.
30.如图,在△ABC中,BD、CE分别是边AC、AB上的中线,BD与CE相交于点O,点M、N分别是OB、OC的中点.
(1)求证:EN与DM互相平分;
(2)若AB=AC,判断四边形DEMN的形状,并说明理由.
答案
一.选择题
A.B.C.B.D.B.D.B.D.B.C.D.
二.填空题
13.2.
14.2.
15.120°.
16.38.
17..
18.6.
19..
20.1.5.
三.解答题
21.解:(1)∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,DEBC,
∵CFBC,
∴DE=FC,
∵DE∥FC,
∴四边形DCFE是平行四边形,
∴CD=EF;
(2)猜想:△ABC的面积=四边形BDEF的面积,理由如下:
∵DE为△ABC的中位线,
∴DE∥BC,DEBC
∴△ADE的面积=△DEC的面积,
∴四边形DCFE是平行四边形,
∴△DEC的面积=△ECF的面积,
∴△ADE的面积=△ECF的面积,
∴△ABC的面积=四边形BDEF的面积.
22.证明:取AD的中点Q,连接EQ、FQ,
∵E,F、Q分别为AB,CD、AD的中点,
∴EQ∥BD,EQBD,FQAC,FQ∥AC,
∴∠QEF=∠OMN,∠QFE=∠ONM,
∵AC=BD,
∴QE=QF,
∴∠QEF=∠QFE,
∴∠OMN=∠ONM,
∴OM=ON,即△OMN是等腰三角形.
23.证明:∵E,G为AB、BC中点,
∴EGAC,EG∥AC,
∴∠FEG=∠OQP,
同理,FGBD,FG∥BD,
∴∠EFG=∠OPQ,
∵AC=BD,
∴EG=FG,
∴∠FEG=∠EFG,
∴∠OPQ=∠OQP,
∴OP=OQ.
24.证明:∵E,F分别是AD,DC的中点,
∴EF是△ADC的中位线,
∴,
∵AB⊥BC,M是AC的中点,
∴,
∴EF=BM.
25.解:在△AGF和△ACF中,
,
∴△AGF≌△ACF(ASA).
∴AG=AC=8cm,
∴GF=CF,则BG=AB﹣AG=12﹣8=4(cm).
又∵BE=CE,
∴EF是△BCG的中位线.
∴EFBG=2cm.
答:EF的长为2cm,
26.解:(1)∵AH⊥BC,
∴∠AHB=90°,
∵点D是AB的中点,
∴AD=DHAB;
(2)∵AH⊥BC,
∴∠AHB=∠AHC=90°,
∵点D,E分别是AB,AC的中点,
∴AD=DHAB,AE=HEAC,
∵四边形ADHE的周长是30,
∴AD+AE30=15,
∵△ADE的周长是21,
∴DE=21﹣15=6,
∵点D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE=12.
27.证明:延长AC、BD交于点F,
∵在△ABD和△AFD中,
,
∴△ABD≌△AFD(ASA),
∴AB=AF,BD=DF,
又∵E是BC的中点,即ED是△BCF中位线,
∴DECF(AB﹣AC).
28.证明:连接EH,GH,GF,
∵E、F、G、H分别是BD、BC、AC、AD的中点,
∴AB∥EH∥GF,GH∥BC∥BF.
∴四边形EHGF为平行四边形.
∵GE,HF分别为其对角线,
∴EG、HF互相平分.
29.证明:连接DE,FG,
∵BD,CE是△ABC的中线,
∴D,E是AB,AC的中点,
∴DE∥BC,DEBC,
同理:FG∥BC,FGBC,
∴DE∥FG,DE=FG,
∴四边形DEFG是平行四边形,
∴EF∥DG,EF=DG.
30.解:
(1)证明:∵BD、CE分别是边AC、AB上的中线,
∴点D、E分别是边AC、AB的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DEBC,
同理得:MN∥BC,MNBC,
∴DE∥MN,DE=MN,
∴四边形DEMN是平行四边形,
∴EN与DM互相平分;
(2)四边形DEMN是矩形;
理由:∵AB=AC
∴∠EBC=∠DCB
∵点D、E分别是边AC、AB的中点
∴EB=DC
又BC=CB
∴△EBC≌△DCB,
∴EC=DB
∵EN与DM互相平分,点M、N分别是OB、OC的中点,
∴OEEC,ODBD
∴OE=OD,
即EN=DM,
∴□DEMN是矩形.
一.选择题
1.顺次连结对角线互相垂直的四边形各边中点所构成的四边形一定是( )
A.矩形 B.菱形 C.正方形 D.不确定
2.△ABC中,AB=7,BC=6,AC=5,点D、E、F分别是三边的中点,则△DEF的周长为( )
A.4.5 B.9 C.10 D.12
3.已知等腰三角形的两条中位线的长分别为3和5,则此等腰三角形的周长为( )
A.22 B.26 C.22或26 D.13
4.如图,在△ABC中,D是AC的中点,且BD⊥AC,DE∥BC,交AB于点E,BC=7cm,AC=6cm,则△AED的周长等于( )
A.12cm B.10cm C.7cm D.9cm
5.四边形ABCD中,AB=1,CD=4,M、N分别是AD、BC的中点,则线段MN的取值范围是( )
A.3<MN<5 B.3<MN≤5 C.MN D.MN
6.如图,D、E分别为△ABC中AB、AC边上的中点,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
A.1 B. C.2 D.
7.如图,四边形ABCD中,∠A=90°,AB=2,AD=2,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A.3 B.2 C.4 D.2
8.如图,在四边形ABCD中,AB=6,BC=10,∠A=130°,∠D=100°,AD=CD.若点E,F分别是边AD,CD的中点,则EF的长是( )
A.3 B.4 C.2 D.
9.如图,依次连接任意四边形ABCD四条边的中点得到四边形EFGH,添加下列条件能判断四边形EFGH是菱形的是( )
A.AB=BC B.AB⊥BC C.AC⊥BD D.AC=BD
10.已知在四边形ABCD中,AB=3,CD=5,M,N分别是AD,BC的中点,则线段MN的取值范围是( )
A.1<MN<4 B.1<MN≤4 C.2<MN<8 D.2<MN≤8
11.如图,在Rt△ABC中,∠B=90°,BC=5,AB=12,点D,E分别是AB,AC的中点,CF平分Rt△ABC的一个外角∠ACM,交DE的延长线于点F,则DF的长为( )
A.5 B.8.5 C.9 D.12
12.如图,在四边形ABCD中,P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠EPF=140°,则∠EFP的度数是( )
A.50° B.40° C.30° D.20°
二.填空题
13.如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,E、F分别为DB、BC的中点,若AB=8,则EF= .
14.如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CDBD,连接DM、DN、MN.若AB=4,则DN= .
15.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是 .
16.如图,△ABC,点D,E在边BC上,∠ABC的平分线垂直AE,垂足为N,∠ACB的平分线垂直AD,垂足为M,若BC=16,MN=3,则△ABC的周长为 .
17.如图,在四边形BCDE中,BC⊥CD,DE⊥CD,AB⊥AE,垂足分别为C,D,A,BC≠AC,点M,N,F分别为AB,AE,BE的中点,连接MN,MF,NF.当BC=4,DE=5,∠FMN=45°时,则BE的长为 .
18.如图,AD为△ABC中∠BAC的外角平分线,BD⊥AD于点D,E为BC中点,DE=4,AC=2,则AB长为 .
19.如图,Rt△ABC中,∠C=90°,BC=6,AC=10,D,E分别是AC和BC上的点,且CE=2,CD=4,连接BD,AE.G、H分别是AE和BD的中点,连接GH,则线段GH的长为 .
20.如图,△ABC中,AB=10,AC=7,AD平分∠BAC,AE是BC边上的中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为 .
三.解答题
21.如图,在等边△ABC中,D,E分别为AB,AC的中点,延长BC至点F,使CFBC,连结CD和EF.
(1)求证:CD=EF;
(2)猜想:△ABC的面积与四边形BDEF的面积的关系,并说明理由.
22.一个对角线相等的四边形ABCD,E、F分别为AB,CD的中点,EF分别交对角线BD,AC于M,N,求证:△OMN是等腰三角形.
23.如图,在四边形ABCD中,对角线AC=BD,E,F为AB、CD的中点,连接EF交BD、AC于P、Q,取BC中点G,连EG、FG,求证:OP=OQ.
24.如图,在四边形ABCD中,AB⊥BC,连接AC,E,F,M分别是AD,DC,AC的中点,连接EF,BM.求证:EF=BM.
25.如图,在△ABC中,AB=12cm,AC=8cm,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于点F,交AB于点G,连接EF,求线段EF的长.
26.如图,△ABC中,AH⊥BC于点H,点D,E分别是AB,AC的中点,连接DH,EH,DE.
(1)求证:AD=DH;
(2)若四边形ADHE的周长是30,△ADE的周长是21,求BC的长.
27.如图,已知AO是△ABC的∠A的平分线,BD⊥AO的延长线于D,E是BC的中点.
求证:DE(AB﹣AC)
28.已知:△ABC中,D是BC上的一点,E、F、G、H分别是BD、BC、AC、AD的中点,
求证:EG、HF互相平分.
29.△ABC的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证:EF∥DG,且EF=DG.
30.如图,在△ABC中,BD、CE分别是边AC、AB上的中线,BD与CE相交于点O,点M、N分别是OB、OC的中点.
(1)求证:EN与DM互相平分;
(2)若AB=AC,判断四边形DEMN的形状,并说明理由.
答案
一.选择题
A.B.C.B.D.B.D.B.D.B.C.D.
二.填空题
13.2.
14.2.
15.120°.
16.38.
17..
18.6.
19..
20.1.5.
三.解答题
21.解:(1)∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,DEBC,
∵CFBC,
∴DE=FC,
∵DE∥FC,
∴四边形DCFE是平行四边形,
∴CD=EF;
(2)猜想:△ABC的面积=四边形BDEF的面积,理由如下:
∵DE为△ABC的中位线,
∴DE∥BC,DEBC
∴△ADE的面积=△DEC的面积,
∴四边形DCFE是平行四边形,
∴△DEC的面积=△ECF的面积,
∴△ADE的面积=△ECF的面积,
∴△ABC的面积=四边形BDEF的面积.
22.证明:取AD的中点Q,连接EQ、FQ,
∵E,F、Q分别为AB,CD、AD的中点,
∴EQ∥BD,EQBD,FQAC,FQ∥AC,
∴∠QEF=∠OMN,∠QFE=∠ONM,
∵AC=BD,
∴QE=QF,
∴∠QEF=∠QFE,
∴∠OMN=∠ONM,
∴OM=ON,即△OMN是等腰三角形.
23.证明:∵E,G为AB、BC中点,
∴EGAC,EG∥AC,
∴∠FEG=∠OQP,
同理,FGBD,FG∥BD,
∴∠EFG=∠OPQ,
∵AC=BD,
∴EG=FG,
∴∠FEG=∠EFG,
∴∠OPQ=∠OQP,
∴OP=OQ.
24.证明:∵E,F分别是AD,DC的中点,
∴EF是△ADC的中位线,
∴,
∵AB⊥BC,M是AC的中点,
∴,
∴EF=BM.
25.解:在△AGF和△ACF中,
,
∴△AGF≌△ACF(ASA).
∴AG=AC=8cm,
∴GF=CF,则BG=AB﹣AG=12﹣8=4(cm).
又∵BE=CE,
∴EF是△BCG的中位线.
∴EFBG=2cm.
答:EF的长为2cm,
26.解:(1)∵AH⊥BC,
∴∠AHB=90°,
∵点D是AB的中点,
∴AD=DHAB;
(2)∵AH⊥BC,
∴∠AHB=∠AHC=90°,
∵点D,E分别是AB,AC的中点,
∴AD=DHAB,AE=HEAC,
∵四边形ADHE的周长是30,
∴AD+AE30=15,
∵△ADE的周长是21,
∴DE=21﹣15=6,
∵点D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE=12.
27.证明:延长AC、BD交于点F,
∵在△ABD和△AFD中,
,
∴△ABD≌△AFD(ASA),
∴AB=AF,BD=DF,
又∵E是BC的中点,即ED是△BCF中位线,
∴DECF(AB﹣AC).
28.证明:连接EH,GH,GF,
∵E、F、G、H分别是BD、BC、AC、AD的中点,
∴AB∥EH∥GF,GH∥BC∥BF.
∴四边形EHGF为平行四边形.
∵GE,HF分别为其对角线,
∴EG、HF互相平分.
29.证明:连接DE,FG,
∵BD,CE是△ABC的中线,
∴D,E是AB,AC的中点,
∴DE∥BC,DEBC,
同理:FG∥BC,FGBC,
∴DE∥FG,DE=FG,
∴四边形DEFG是平行四边形,
∴EF∥DG,EF=DG.
30.解:
(1)证明:∵BD、CE分别是边AC、AB上的中线,
∴点D、E分别是边AC、AB的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DEBC,
同理得:MN∥BC,MNBC,
∴DE∥MN,DE=MN,
∴四边形DEMN是平行四边形,
∴EN与DM互相平分;
(2)四边形DEMN是矩形;
理由:∵AB=AC
∴∠EBC=∠DCB
∵点D、E分别是边AC、AB的中点
∴EB=DC
又BC=CB
∴△EBC≌△DCB,
∴EC=DB
∵EN与DM互相平分,点M、N分别是OB、OC的中点,
∴OEEC,ODBD
∴OE=OD,
即EN=DM,
∴□DEMN是矩形.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
