人教版六年级下册数学第5单元《鸽巢问题》课件(17张ppt)
文档属性
| 名称 | 人教版六年级下册数学第5单元《鸽巢问题》课件(17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 69.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 22:39:26 | ||
图片预览





文档简介
(共17张PPT)
问 题
(抽屉原理)
鸽 巢
游戏导入
一副牌,取出大小王,还剩52张,请5人每人随意抽一张,我知道至少有2张牌是同花色的。相信吗?请五位同学揭晓答案,老师猜的对吗
返回目录
探究新知(一)
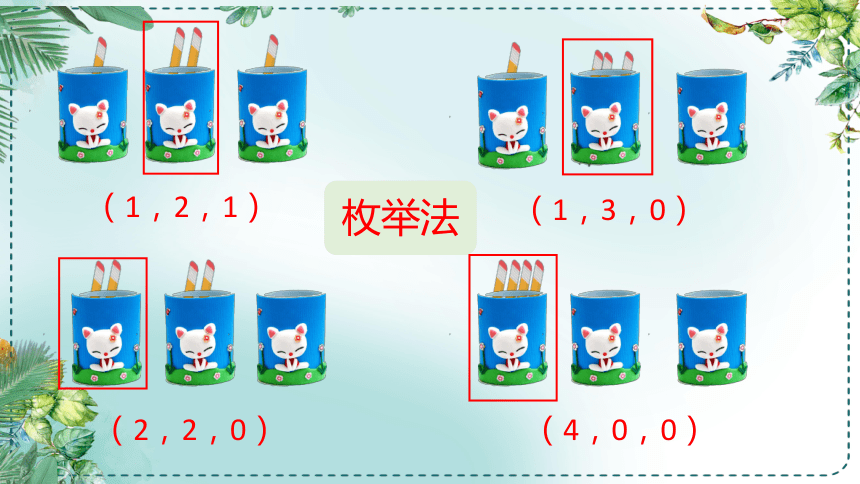
把4支铅笔放进3个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。为什么呢?
(1,2,1)
(1,3,0)
(2,2,0)
(4,0,0)
枚举法
不管怎么放,总有一个笔筒里至少放进( )支笔。
2
假设法
4÷3=1(支)...... 1(支) 1+1=2(支)
摆一摆,画一画。
5支铅笔放进4个笔筒中,总有一个笔筒里至少有( )支铅笔。
6支铅笔放进5个笔筒中,总有一个笔筒里至少有( )支铅笔。
10支铅笔放进9个笔筒呢?
100支铅笔放进99个笔筒呢?
2
2
2支
2支
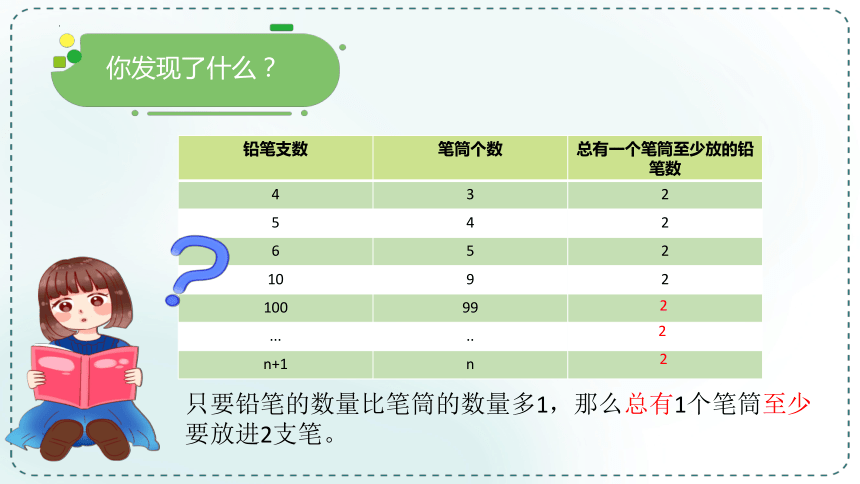
你发现了什么?
铅笔支数 笔筒个数 总有一个笔筒至少放的铅笔数
4 3 2
5 4 2
6 5 2
10 9 2
100 99
... ..
n+1 n
2
2
2
只要铅笔的数量比笔筒的数量多1,那么总有1个笔筒至少要放进2支笔。
把(n+1)个物体任意放进n个鸽巢中(n是非0自然数),一定有一个鸽巢中至少放进了2个物体。
算式表示:
(n+1)÷n=1……1
1+1=2(个)
1.某一小学六年级有367名学生,其中至少有两人是同一天生日。请说明理由。
一年最多有366天,我们把366天看成“366个鸽巢”,把367名学生放进“366个鸽巢”中,必然有一个鸽巢至少放进2名学生,即至少有2名同学是同一天生日的。
用除法算式表示:367÷366=1(名)......1(名)
1+1=2(名)
小试牛刀
返回目录
把7本数学书放进3个抽屉,不管怎么放,总有一个抽屉里至少放进3本书。为什么?
假设法
7本书平均放在3个抽屉中,每个抽屉放2本,还剩余1本,不管放在哪个抽屉中,总有一个抽屉里至少放进3本书。
探索新知(二)
枚举法:
列式:
把7分解成3个数,共有8种情况。每一种情况中,至少有一个数大于或等于3。
7÷3=2(本)......1(本)
2+1=3(本)
如果有 8 本书会怎么样呢?
用算式表示:8÷3=2(本)......2(本)
2+1=3(本)
10 本书呢?
用算式表示:10÷3=3(本)......1(本)
3+1=4(本)
规律:如果物体数除以抽屉数有余数,用所得的商加 1 。
物体数÷抽屉数=商......余数
至少数=商+1
资料卡
小视频
下一页
返回目录
11只鸽子飞进了4个鸽笼,总有一个鸽笼至少飞进了3只鸽子。为什么?
11÷4=2(只)…… 3(只)
2+1=3(只)
巩固提升
返回目录
生1
把(n+1)个物体任意放进n个鸽巢中(n是非0自然数),一定有一个鸽巢中至少放进了2个物体。
生2
我们可以用枚举法、假设法,列式等方式来解决鸽巢问题。
生3
我们可以用以下公式快速解决这类问题
物体数÷抽屉数=商......余数 至少数=商+1
通过本节课的学习你有哪些新的收获呢?
......
课堂小结
返回目录
课外作业
找一找生活中有哪些事物或者现象可以用抽屉原理来解释。
。
返回目录
谢谢观看!
返回
问 题
(抽屉原理)
鸽 巢
游戏导入
一副牌,取出大小王,还剩52张,请5人每人随意抽一张,我知道至少有2张牌是同花色的。相信吗?请五位同学揭晓答案,老师猜的对吗
返回目录
探究新知(一)
把4支铅笔放进3个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。为什么呢?
(1,2,1)
(1,3,0)
(2,2,0)
(4,0,0)
枚举法
不管怎么放,总有一个笔筒里至少放进( )支笔。
2
假设法
4÷3=1(支)...... 1(支) 1+1=2(支)
摆一摆,画一画。
5支铅笔放进4个笔筒中,总有一个笔筒里至少有( )支铅笔。
6支铅笔放进5个笔筒中,总有一个笔筒里至少有( )支铅笔。
10支铅笔放进9个笔筒呢?
100支铅笔放进99个笔筒呢?
2
2
2支
2支
你发现了什么?
铅笔支数 笔筒个数 总有一个笔筒至少放的铅笔数
4 3 2
5 4 2
6 5 2
10 9 2
100 99
... ..
n+1 n
2
2
2
只要铅笔的数量比笔筒的数量多1,那么总有1个笔筒至少要放进2支笔。
把(n+1)个物体任意放进n个鸽巢中(n是非0自然数),一定有一个鸽巢中至少放进了2个物体。
算式表示:
(n+1)÷n=1……1
1+1=2(个)
1.某一小学六年级有367名学生,其中至少有两人是同一天生日。请说明理由。
一年最多有366天,我们把366天看成“366个鸽巢”,把367名学生放进“366个鸽巢”中,必然有一个鸽巢至少放进2名学生,即至少有2名同学是同一天生日的。
用除法算式表示:367÷366=1(名)......1(名)
1+1=2(名)
小试牛刀
返回目录
把7本数学书放进3个抽屉,不管怎么放,总有一个抽屉里至少放进3本书。为什么?
假设法
7本书平均放在3个抽屉中,每个抽屉放2本,还剩余1本,不管放在哪个抽屉中,总有一个抽屉里至少放进3本书。
探索新知(二)
枚举法:
列式:
把7分解成3个数,共有8种情况。每一种情况中,至少有一个数大于或等于3。
7÷3=2(本)......1(本)
2+1=3(本)
如果有 8 本书会怎么样呢?
用算式表示:8÷3=2(本)......2(本)
2+1=3(本)
10 本书呢?
用算式表示:10÷3=3(本)......1(本)
3+1=4(本)
规律:如果物体数除以抽屉数有余数,用所得的商加 1 。
物体数÷抽屉数=商......余数
至少数=商+1
资料卡
小视频
下一页
返回目录
11只鸽子飞进了4个鸽笼,总有一个鸽笼至少飞进了3只鸽子。为什么?
11÷4=2(只)…… 3(只)
2+1=3(只)
巩固提升
返回目录
生1
把(n+1)个物体任意放进n个鸽巢中(n是非0自然数),一定有一个鸽巢中至少放进了2个物体。
生2
我们可以用枚举法、假设法,列式等方式来解决鸽巢问题。
生3
我们可以用以下公式快速解决这类问题
物体数÷抽屉数=商......余数 至少数=商+1
通过本节课的学习你有哪些新的收获呢?
......
课堂小结
返回目录
课外作业
找一找生活中有哪些事物或者现象可以用抽屉原理来解释。
。
返回目录
谢谢观看!
返回
