苏科版八年级数学下册试题 9.1图形的旋转(含答案)
文档属性
| 名称 | 苏科版八年级数学下册试题 9.1图形的旋转(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 175.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-04 08:32:24 | ||
图片预览



文档简介
9.1图形的旋转
一、选择题.
1.如图,点A、B、C、D、O都在方格纸的格点上,若△CDO是由△ABO绕点O按顺时针方向旋转而得,则旋转的角度是( )
A.30° B.45° C.60° D.90°
2.如图,在△ABC中,∠B=50°,将△ABC绕点A按逆时针方向旋转得到△A′B′C′.若点B′恰好落在BC边上,则∠CB′C′的度数为( )
A.50° B.60° C.80° D.100°
3.如图,等边三角形ABC与等边三角形EFB共端点B,BC=2,BF,△EFB绕点B旋转,∠BCF的最大度数( )
A.30° B.45° C.60° D.90°
4.如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=2,BD=3,则CD的长为( )
A. B.4 C. D.
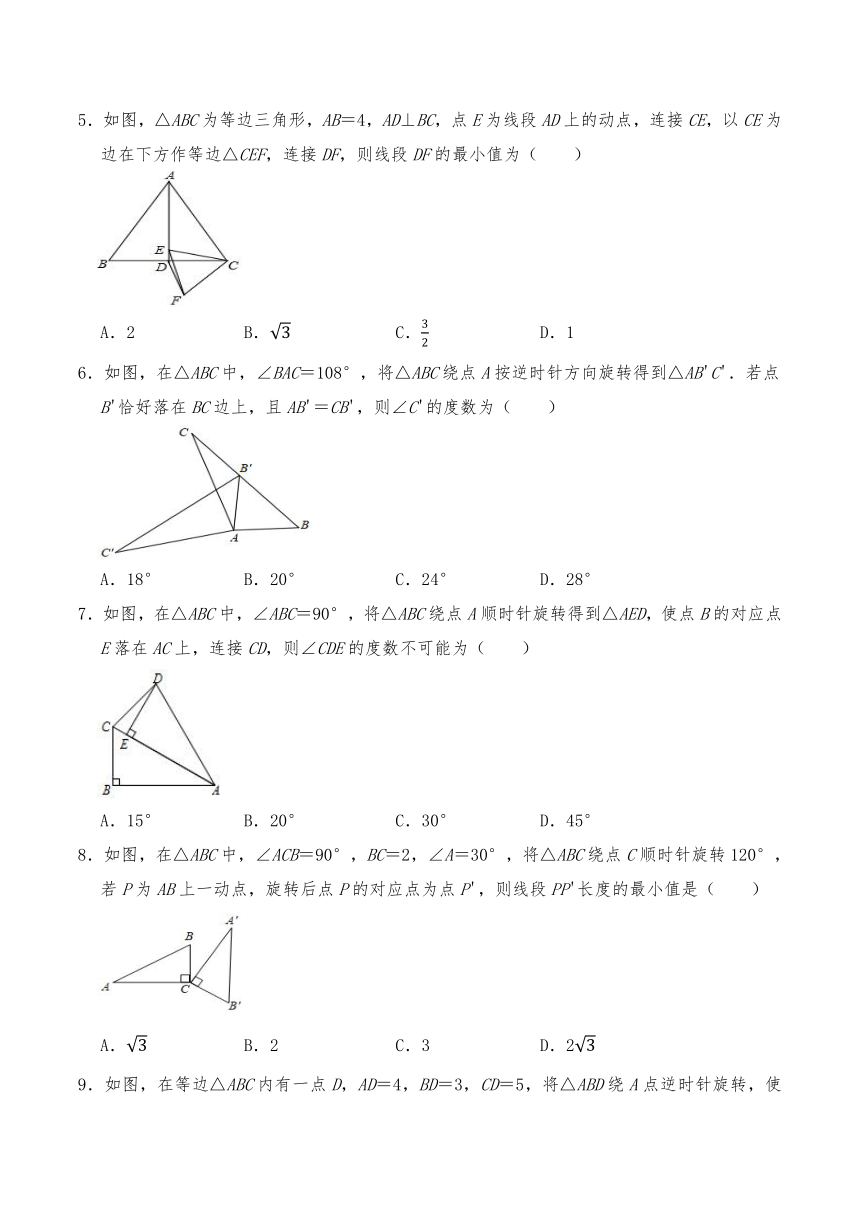
5.如图,△ABC为等边三角形,AB=4,AD⊥BC,点E为线段AD上的动点,连接CE,以CE为边在下方作等边△CEF,连接DF,则线段DF的最小值为( )
A.2 B. C. D.1
6.如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'恰好落在BC边上,且AB'=CB',则∠C'的度数为( )
A.18° B.20° C.24° D.28°
7.如图,在△ABC中,∠ABC=90°,将△ABC绕点A顺时针旋转得到△AED,使点B的对应点E落在AC上,连接CD,则∠CDE的度数不可能为( )
A.15° B.20° C.30° D.45°
8.如图,在△ABC中,∠ACB=90°,BC=2,∠A=30°,将△ABC绕点C顺时针旋转120°,若P为AB上一动点,旋转后点P的对应点为点P',则线段PP'长度的最小值是( )
A. B.2 C.3 D.2
9.如图,在等边△ABC内有一点D,AD=4,BD=3,CD=5,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则四边形ADCE的面积为( )
A.12 B. C. D.
10.如图,在Rt△ABC中,∠C=90°,把△ABC绕AC边的中点M旋转后得△DEF,若直角顶点F恰好落在AB边上,且DE边交AB边于点G,若AC=4,BC=3,则AG的长为( )
A. B. C. D.1
二、填空题
11.如图,△COD是由△AOB绕点O按顺时针方向旋转40°后得到的图形,点C恰好在边AB上.若∠AOD=100°,则∠D的度数是 °.
12.如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,则∠A的度数是 .
13.如图,△ABC中,∠BAC=95°,将△ABC绕点A逆时针旋转60°得到△AB'C',∠B'AC的大小为 °.
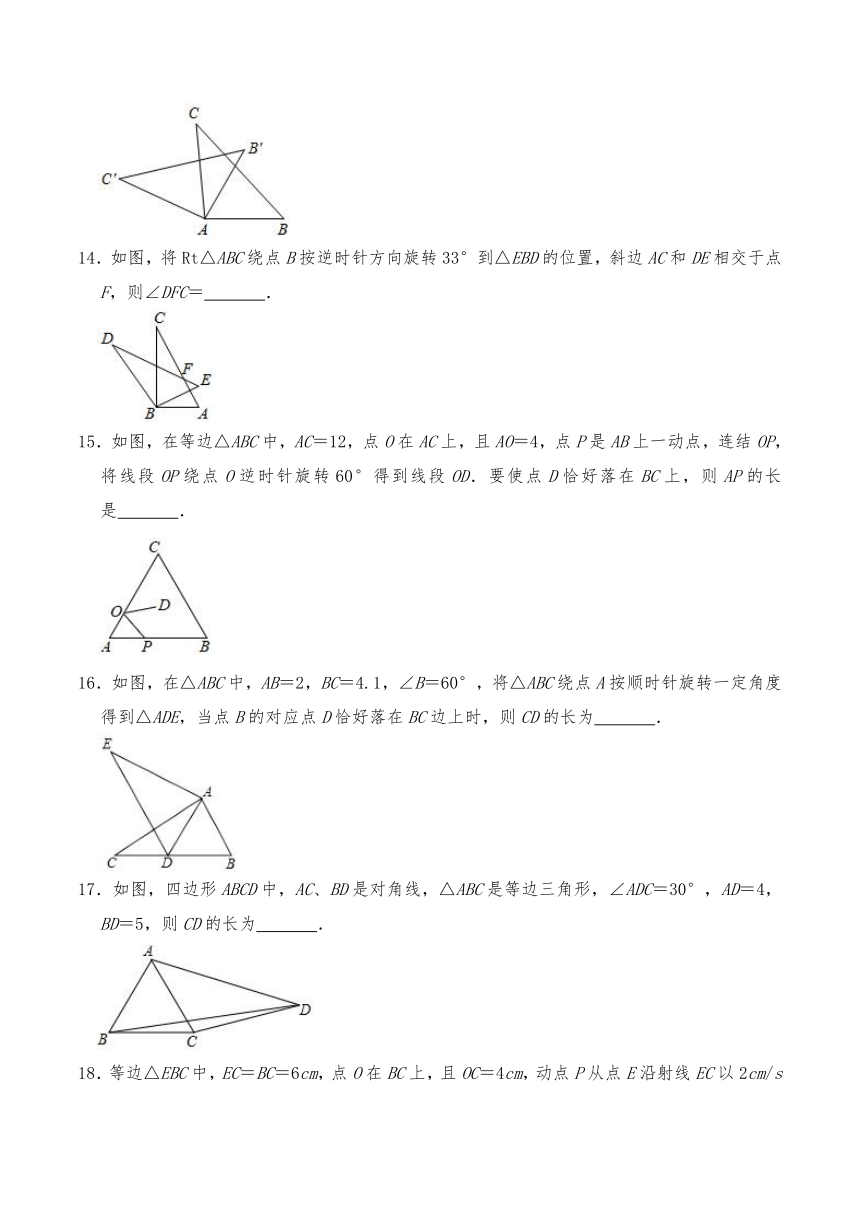
14.如图,将Rt△ABC绕点B按逆时针方向旋转33°到△EBD的位置,斜边AC和DE相交于点F,则∠DFC= .
15.如图,在等边△ABC中,AC=12,点O在AC上,且AO=4,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是 .
16.如图,在△ABC中,AB=2,BC=4.1,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为 .
17.如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=4,BD=5,则CD的长为 .
18.等边△EBC中,EC=BC=6cm,点O在BC上,且OC=4cm,动点P从点E沿射线EC以2cm/s速度运动,连结OP,将线段OP绕点O逆时针旋转120°得到线段OF.则当点F运动 s时,点F恰好落在射线EB上.
三、解答题
19.如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上.
(1)将△ABC向右平移6个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)画出△A1B1C1关于点O的中心对称图形△A2B2C2;
(3)若将△ABC绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
20.如图,在10×10的网格中建立平面直角坐标系,△ABC是格点三角形(顶点在网格线的交点上).
(1)先作△ABC关于原点O的成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位得到△A2B2C2;
(2)A2点的坐标为 ;
(3)请直接写出CC1+C1C2= .
21.如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.求证:AB⊥AE.
22.如图,已知△ABC是等边三角形,在△ABC外有一点D,连接AD,BD,CD,将△ACD绕点A按顺时针方向旋转得到△ABE,AD与BE交于点F,∠BFD=97°(sin37°=0.6).
(1)求∠ADC的大小;
(2)若∠BDC=7°,BD=3,CD=5,求AD的长.
23.如图,△ABC与△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE.
(1)将△ADE旋转,使得D、E、B三点在一条直线上时,求证:BD=CE;
(2)在(1)的条件下,当BC=10,BE=6时,求DE的长.
24.如图1,等边三角形△ABC中,D为△ABC内一点,将△CAD绕点C按逆时针方向旋转角60°得到△CBE,点A,D的对应点分别为点B、E,且A、D、E三点在同一直线上.
(1)填空:∠CDE= ;
(2)若过点C作CF⊥AE于点F,然后探究线段CF,AE,BE之间的数量关系,并证明你的结论.
答案
一、选择题.
D.C.C.A.D.C.D.C.C.A.
二、填空题
11.50.
12.70°.
13.35.
14.33°.
15.8.
16.2.1.
17.3.
18.4.
三、解答题
19.(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)根据图形可知:
旋转中心的坐标为:(﹣3,0).
20.(1)如图,△A1B1C1和△A2B2C2为所作;
(2)A2点的坐标为(3,4);
(3)CC1+C1C224.
故答案为(3,4),24.
21.证明:∵∠ACB=90°,AC=BC,
∴△ABC为等腰直角三角形,
∴∠B=∠BAC=45°,
∵线段CD绕点C顺时针旋转90°至CE位置,
∴CD=CE,∠DCE=90°,
∴△CBD绕点C顺时针旋转90°得到△CAE,
∴∠CAE=∠CBD=45°,
∴∠BAE=∠BAC+∠CAE=90°,
∴AB⊥AE.
22.(1)∵将△ACD绕点A按顺时针方向旋转得到△ABE,
∴AB=AC,∠ADC=∠E,∠CAB=∠DAE=60°,
∵∠BFD=97°=∠AFE,
∴∠E=180°﹣97°﹣60°=23°,
∴∠ADC=∠E=23°;
(2)如图,连接DE,
∵AD=AE,∠DAE=60°,
∴△AED是等边三角形,
∴∠ADE=60°,AD=DE,
∵将△ACD绕点A按顺时针方向旋转得到△ABE,
∴△ACD≌△ABE,
∴CD=BE=5,
∵∠BDC=7°,∠ADC=23°,∠ADE=60°,
∴∠BDE=90°,
∴DE4,
∴AD=DE=4.
23.证明:(1)∵∠BAC=∠DAE=90°,
∴∠BAC+∠EAB=∠DAE+∠EAB,
即∠DAB=∠EAC,
在△ABD和△ACE中,
,
∴△DAB≌△EAC(SAS),
∴DB=EC;
(2)由(1)知△DAB≌△EAB,
∴∠DBA=∠ECA,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,
即∠ABC+(∠BCE+∠ACE)=90°,
∴∠ABC+∠DBA+∠BCE=90°,
即∠DBA+∠BCE=90°,
∴∠BEC=90°,
∵BC=10,BE=6,
∴EC2=BC2﹣BE2=102﹣62=64,
∴EC=8,
∴DE=DB﹣BE=DB﹣CE=8﹣6=2.
24.(1)∵如图,
∵将△CAD绕点C按逆时针方向旋转角60°得到△CBE,
∴△CAD≌△CBE,
∴CD=CE,∠DCE=60°,
∴△CDE是等边三角形,
∴∠CDE=60°,
故答案为:60°;
(2)AE=BECF,
理由如下:
∵将△CAD绕点C按逆时针方向旋转角60°得到△CBE,
∴BE=AD,
∵△CDE是等边三角形,CF⊥AE,
∴DF=EF,∠DCF=30°,
∴CFDF,
∴DFCF,
∵AE=AD+DE,
∴AE=BECF.
一、选择题.
1.如图,点A、B、C、D、O都在方格纸的格点上,若△CDO是由△ABO绕点O按顺时针方向旋转而得,则旋转的角度是( )
A.30° B.45° C.60° D.90°
2.如图,在△ABC中,∠B=50°,将△ABC绕点A按逆时针方向旋转得到△A′B′C′.若点B′恰好落在BC边上,则∠CB′C′的度数为( )
A.50° B.60° C.80° D.100°
3.如图,等边三角形ABC与等边三角形EFB共端点B,BC=2,BF,△EFB绕点B旋转,∠BCF的最大度数( )
A.30° B.45° C.60° D.90°
4.如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=2,BD=3,则CD的长为( )
A. B.4 C. D.
5.如图,△ABC为等边三角形,AB=4,AD⊥BC,点E为线段AD上的动点,连接CE,以CE为边在下方作等边△CEF,连接DF,则线段DF的最小值为( )
A.2 B. C. D.1
6.如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B'恰好落在BC边上,且AB'=CB',则∠C'的度数为( )
A.18° B.20° C.24° D.28°
7.如图,在△ABC中,∠ABC=90°,将△ABC绕点A顺时针旋转得到△AED,使点B的对应点E落在AC上,连接CD,则∠CDE的度数不可能为( )
A.15° B.20° C.30° D.45°
8.如图,在△ABC中,∠ACB=90°,BC=2,∠A=30°,将△ABC绕点C顺时针旋转120°,若P为AB上一动点,旋转后点P的对应点为点P',则线段PP'长度的最小值是( )
A. B.2 C.3 D.2
9.如图,在等边△ABC内有一点D,AD=4,BD=3,CD=5,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则四边形ADCE的面积为( )
A.12 B. C. D.
10.如图,在Rt△ABC中,∠C=90°,把△ABC绕AC边的中点M旋转后得△DEF,若直角顶点F恰好落在AB边上,且DE边交AB边于点G,若AC=4,BC=3,则AG的长为( )
A. B. C. D.1
二、填空题
11.如图,△COD是由△AOB绕点O按顺时针方向旋转40°后得到的图形,点C恰好在边AB上.若∠AOD=100°,则∠D的度数是 °.
12.如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,则∠A的度数是 .
13.如图,△ABC中,∠BAC=95°,将△ABC绕点A逆时针旋转60°得到△AB'C',∠B'AC的大小为 °.
14.如图,将Rt△ABC绕点B按逆时针方向旋转33°到△EBD的位置,斜边AC和DE相交于点F,则∠DFC= .
15.如图,在等边△ABC中,AC=12,点O在AC上,且AO=4,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是 .
16.如图,在△ABC中,AB=2,BC=4.1,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为 .
17.如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=4,BD=5,则CD的长为 .
18.等边△EBC中,EC=BC=6cm,点O在BC上,且OC=4cm,动点P从点E沿射线EC以2cm/s速度运动,连结OP,将线段OP绕点O逆时针旋转120°得到线段OF.则当点F运动 s时,点F恰好落在射线EB上.
三、解答题
19.如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上.
(1)将△ABC向右平移6个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)画出△A1B1C1关于点O的中心对称图形△A2B2C2;
(3)若将△ABC绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
20.如图,在10×10的网格中建立平面直角坐标系,△ABC是格点三角形(顶点在网格线的交点上).
(1)先作△ABC关于原点O的成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位得到△A2B2C2;
(2)A2点的坐标为 ;
(3)请直接写出CC1+C1C2= .
21.如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.求证:AB⊥AE.
22.如图,已知△ABC是等边三角形,在△ABC外有一点D,连接AD,BD,CD,将△ACD绕点A按顺时针方向旋转得到△ABE,AD与BE交于点F,∠BFD=97°(sin37°=0.6).
(1)求∠ADC的大小;
(2)若∠BDC=7°,BD=3,CD=5,求AD的长.
23.如图,△ABC与△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE.
(1)将△ADE旋转,使得D、E、B三点在一条直线上时,求证:BD=CE;
(2)在(1)的条件下,当BC=10,BE=6时,求DE的长.
24.如图1,等边三角形△ABC中,D为△ABC内一点,将△CAD绕点C按逆时针方向旋转角60°得到△CBE,点A,D的对应点分别为点B、E,且A、D、E三点在同一直线上.
(1)填空:∠CDE= ;
(2)若过点C作CF⊥AE于点F,然后探究线段CF,AE,BE之间的数量关系,并证明你的结论.
答案
一、选择题.
D.C.C.A.D.C.D.C.C.A.
二、填空题
11.50.
12.70°.
13.35.
14.33°.
15.8.
16.2.1.
17.3.
18.4.
三、解答题
19.(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)根据图形可知:
旋转中心的坐标为:(﹣3,0).
20.(1)如图,△A1B1C1和△A2B2C2为所作;
(2)A2点的坐标为(3,4);
(3)CC1+C1C224.
故答案为(3,4),24.
21.证明:∵∠ACB=90°,AC=BC,
∴△ABC为等腰直角三角形,
∴∠B=∠BAC=45°,
∵线段CD绕点C顺时针旋转90°至CE位置,
∴CD=CE,∠DCE=90°,
∴△CBD绕点C顺时针旋转90°得到△CAE,
∴∠CAE=∠CBD=45°,
∴∠BAE=∠BAC+∠CAE=90°,
∴AB⊥AE.
22.(1)∵将△ACD绕点A按顺时针方向旋转得到△ABE,
∴AB=AC,∠ADC=∠E,∠CAB=∠DAE=60°,
∵∠BFD=97°=∠AFE,
∴∠E=180°﹣97°﹣60°=23°,
∴∠ADC=∠E=23°;
(2)如图,连接DE,
∵AD=AE,∠DAE=60°,
∴△AED是等边三角形,
∴∠ADE=60°,AD=DE,
∵将△ACD绕点A按顺时针方向旋转得到△ABE,
∴△ACD≌△ABE,
∴CD=BE=5,
∵∠BDC=7°,∠ADC=23°,∠ADE=60°,
∴∠BDE=90°,
∴DE4,
∴AD=DE=4.
23.证明:(1)∵∠BAC=∠DAE=90°,
∴∠BAC+∠EAB=∠DAE+∠EAB,
即∠DAB=∠EAC,
在△ABD和△ACE中,
,
∴△DAB≌△EAC(SAS),
∴DB=EC;
(2)由(1)知△DAB≌△EAB,
∴∠DBA=∠ECA,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,
即∠ABC+(∠BCE+∠ACE)=90°,
∴∠ABC+∠DBA+∠BCE=90°,
即∠DBA+∠BCE=90°,
∴∠BEC=90°,
∵BC=10,BE=6,
∴EC2=BC2﹣BE2=102﹣62=64,
∴EC=8,
∴DE=DB﹣BE=DB﹣CE=8﹣6=2.
24.(1)∵如图,
∵将△CAD绕点C按逆时针方向旋转角60°得到△CBE,
∴△CAD≌△CBE,
∴CD=CE,∠DCE=60°,
∴△CDE是等边三角形,
∴∠CDE=60°,
故答案为:60°;
(2)AE=BECF,
理由如下:
∵将△CAD绕点C按逆时针方向旋转角60°得到△CBE,
∴BE=AD,
∵△CDE是等边三角形,CF⊥AE,
∴DF=EF,∠DCF=30°,
∴CFDF,
∴DFCF,
∵AE=AD+DE,
∴AE=BECF.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
