苏科版八年级数学下册试题 9.4.3正方形综合问题 专练(含答案)
文档属性
| 名称 | 苏科版八年级数学下册试题 9.4.3正方形综合问题 专练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 355.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-04 08:40:30 | ||
图片预览

文档简介
9.4.3正方形综合问题专练
一.解答题
1.如图,四边形ABCD是正方形,点E是BC边上的动点(不与点B、C重合),将射线AE绕点A按逆时针方向旋转45°后交CD边于点F,AE、AF分别交BD于G、H两点.
(1)当∠BEA=55°时,求∠HAD的度数;
(2)设∠BEA=α,试用含α的代数式表示∠DFA的大小;
(3)点E运动的过程中,试探究∠BEA与∠FEA有怎样的数量关系,并说明理由.
2.如图,正方形ABCD的对角线AC、BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
(1)判断四边形AECF的形状,并证明你的猜想;
(2)若AB=3,BE=3,求四边形AECF的周长.
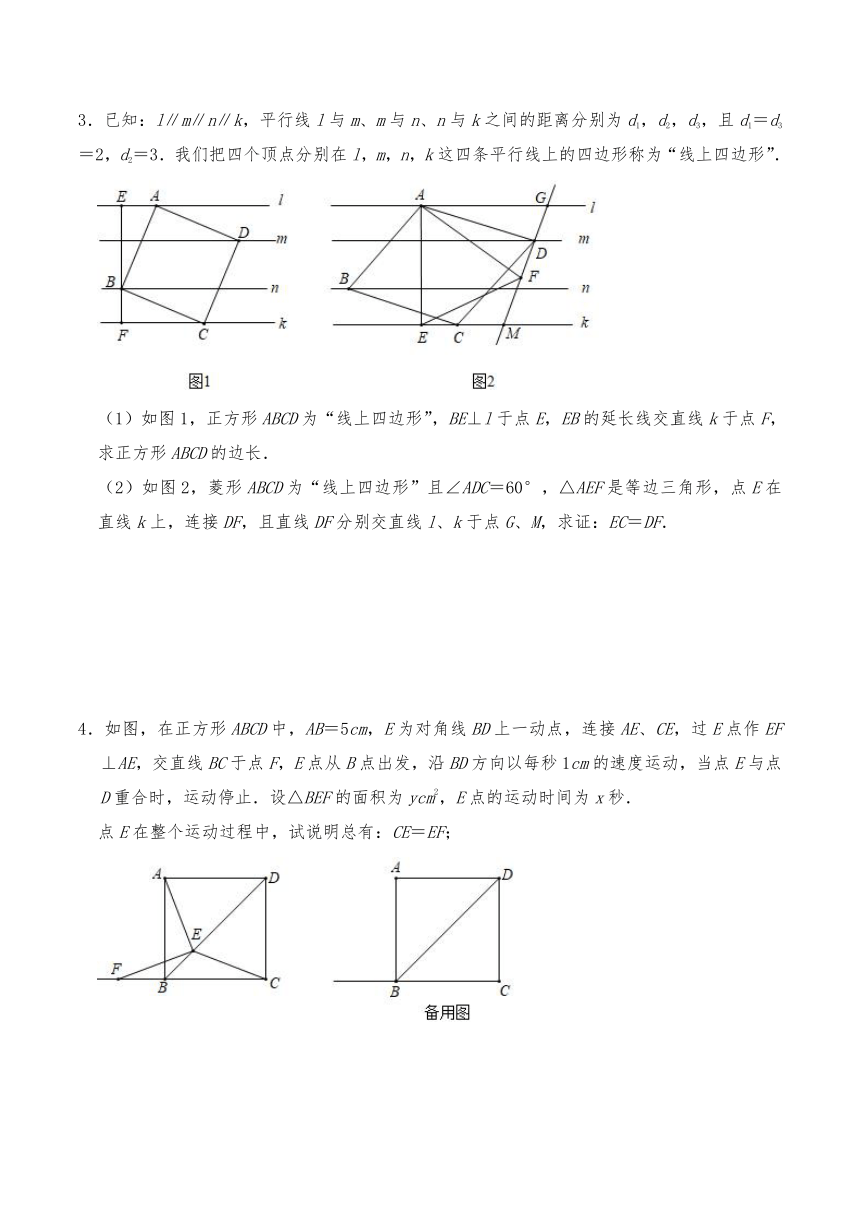
3.已知:l∥m∥n∥k,平行线l与m、m与n、n与k之间的距离分别为d1,d2,d3,且d1=d3=2,d2=3.我们把四个顶点分别在l,m,n,k这四条平行线上的四边形称为“线上四边形”.
(1)如图1,正方形ABCD为“线上四边形”,BE⊥l于点E,EB的延长线交直线k于点F,求正方形ABCD的边长.
(2)如图2,菱形ABCD为“线上四边形”且∠ADC=60°,△AEF是等边三角形,点E在直线k上,连接DF,且直线DF分别交直线l、k于点G、M,求证:EC=DF.
4.如图,在正方形ABCD中,AB=5cm,E为对角线BD上一动点,连接AE、CE,过E点作EF⊥AE,交直线BC于点F,E点从B点出发,沿BD方向以每秒1cm的速度运动,当点E与点D重合时,运动停止.设△BEF的面积为ycm2,E点的运动时间为x秒.
点E在整个运动过程中,试说明总有:CE=EF;
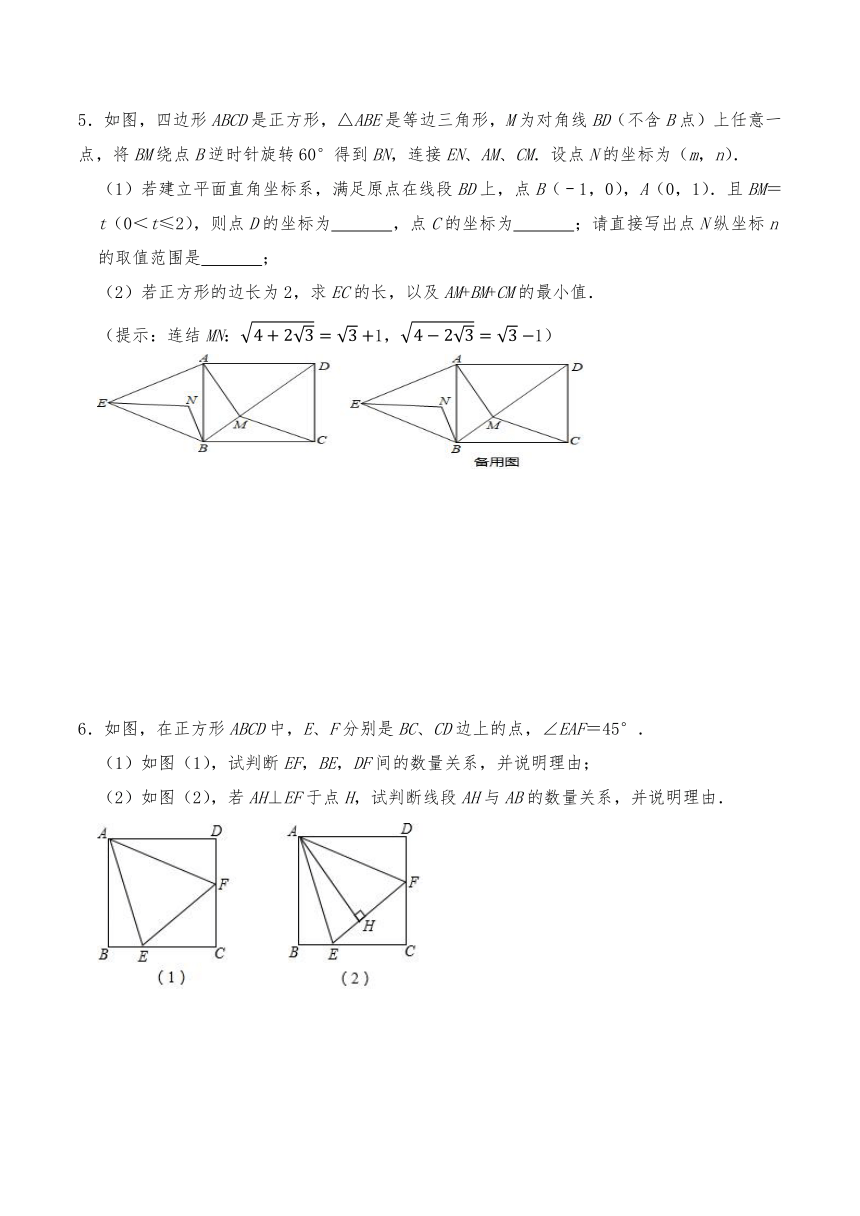
5.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.设点N的坐标为(m,n).
(1)若建立平面直角坐标系,满足原点在线段BD上,点B(﹣1,0),A(0,1).且BM=t(0<t≤2),则点D的坐标为 ,点C的坐标为 ;请直接写出点N纵坐标n的取值范围是 ;
(2)若正方形的边长为2,求EC的长,以及AM+BM+CM的最小值.
(提示:连结MN:1,1)
6.如图,在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°.
(1)如图(1),试判断EF,BE,DF间的数量关系,并说明理由;
(2)如图(2),若AH⊥EF于点H,试判断线段AH与AB的数量关系,并说明理由.
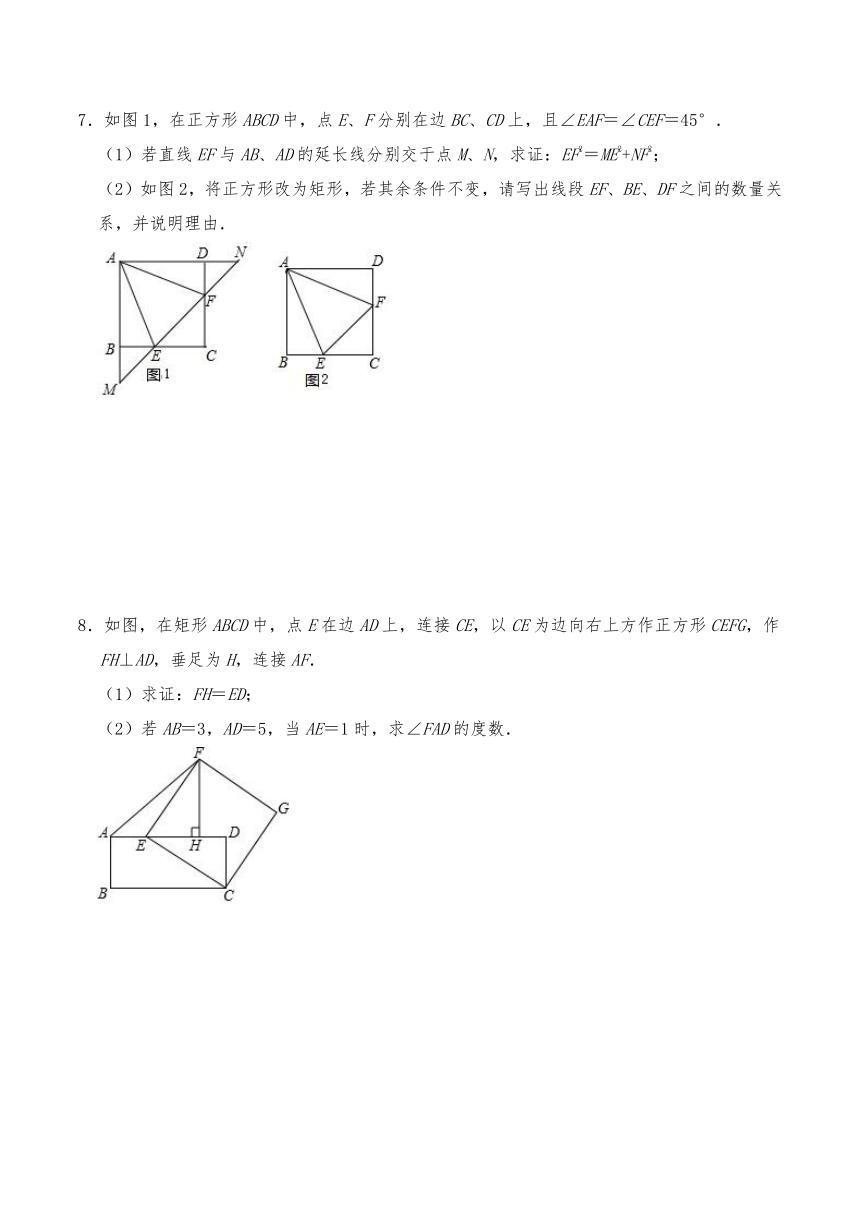
7.如图1,在正方形ABCD中,点E、F分别在边BC、CD上,且∠EAF=∠CEF=45°.
(1)若直线EF与AB、AD的延长线分别交于点M、N,求证:EF2=ME2+NF2;
(2)如图2,将正方形改为矩形,若其余条件不变,请写出线段EF、BE、DF之间的数量关系,并说明理由.
8.如图,在矩形ABCD中,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,垂足为H,连接AF.
(1)求证:FH=ED;
(2)若AB=3,AD=5,当AE=1时,求∠FAD的度数.
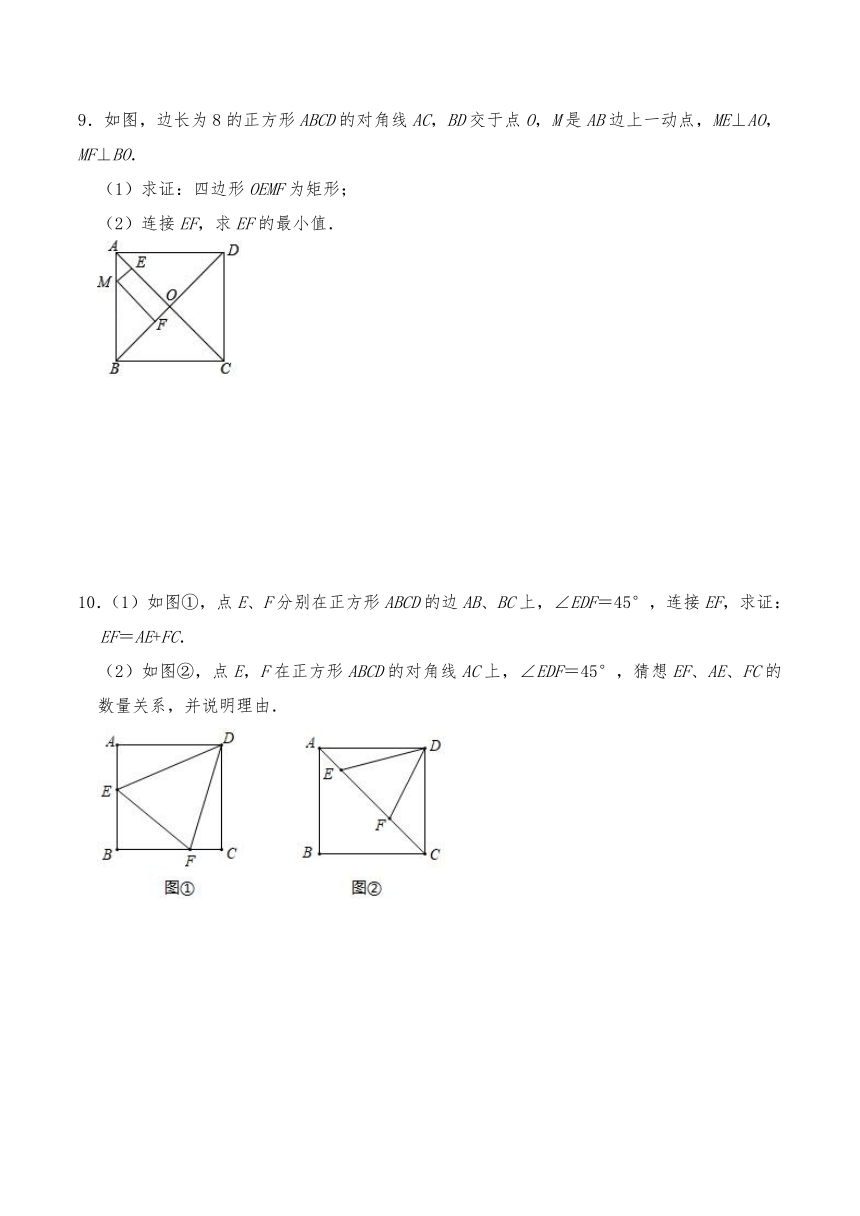
9.如图,边长为8的正方形ABCD的对角线AC,BD交于点O,M是AB边上一动点,ME⊥AO,MF⊥BO.
(1)求证:四边形OEMF为矩形;
(2)连接EF,求EF的最小值.
10.(1)如图①,点E、F分别在正方形ABCD的边AB、BC上,∠EDF=45°,连接EF,求证:EF=AE+FC.
(2)如图②,点E,F在正方形ABCD的对角线AC上,∠EDF=45°,猜想EF、AE、FC的数量关系,并说明理由.
11.如图,在正方形ABCD中,点E是BC上的一点,点F是CD延长线上的一点,且BE=DF,连结AE、AF、EF.求证:△ABE≌△ADF.
12.(1)如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,求证:EF=BE+FD;
(2)如图2,四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足什么关系时,仍有EF=BE+FD,说明理由.
13.如图,在正方形ABCD中,点G在对角线BD上(不与点B,点D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG,
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由.
(2)若正方形ABCD的边长为,∠BAG=75°,求线段BG的长.
14.如图,已知正方形ABCD的边长为6,点E在CD边上,以线段CE为边长在正方形ABCD的外部作正方形CEFG,以线段AD和DE为邻边作矩形ADEH,若S正方形CEFG=S矩形ADEH.
(1)求线段CE的长;
(2)若点M为BC边的中点,连结MD,求证:MD=MG.
15.如图,四边形ABCD是正方形,点E,H分别在BC,AB上,点G在BA的延长线上,且CE=AG,DE⊥CH于F.
(1)求证:四边形GHCD为平行四边形.
(2)在不添加任何辅助线的情况下,请直接写出图中所有与∠ECF互余的角.
16.如图,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且∠PAE=∠E,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数.
17.如图,P为正方形ABCD的对角线上任一点,PE⊥AB于E,PF⊥BC于F.
(1)判断DP与EF的关系,并证明;
(2)若正方形ABCD的边长为6,∠ADP:∠PDC=1:3.求PE的长.
18.如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.
(1)求证:OM=ON.
(2)若正方形ABCD的边长为8,E为OM的中点,求MN的长.
19.(1)如图1,在正方形ABCD中,E是AB上一点,G是AD上一点,∠ECG=45°,那么EG与图中两条线段的和相等?证明你的结论.
(2)请用(1)中所积累的经验和知识完成此题,如图2,在四边形ABCD中,AG∥BC(BC>AG),∠B=90°,AB=BC=12,E是AB上一点,且∠ECG=45°,BE=4,求EG的长?
20.如图,在正方形ABCD中,点E是对角线BD上的一点(DE<BE),连接AE,过点E分别作EF⊥AE交BC于点F,EG⊥BD交BC的延长线于点G.
(1)若AD=2,DE=1,求EG的长度;
(2)求证:FG=AB.
21.如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,经通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明.
22.已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为射线CB上一点.以AD为边做正方形ADEF,连接CF,且点A,F分别在直线BC的两侧.
(1)请直接写出CF,BC,CD三条线段之间的关系;
(2)若正方形ADEF的边长为2,对角线AE,DF相交于点O,连接OC.求OC的长度.
23.如图1,在正方形ABCD中,对角线AC与BD相交于点O,R是AC上任意一点,连接BR,过点A作AQ⊥BR,垂足为点Q,AQ与BD交于点P.
(1)求证:OP=OR;
(2)如图2,若点R在AC的延长线上,AQ⊥BR于点Q,AQ与DB的延长线交于点P,其他条件不变,判断线段DP与AR的数量关系: .
24.四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(1)求证:AM=AD+MC.
(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,试判断AM=AD+MC是否成立?若成立,请给出证明,若不成立,请说明理由;
25.如图,正方形ABCD的边长为2.以对角线BD为边作菱形BEFD.点C,E,F在同一直线上,求CE的长.
26.(1)如图1,已知正方形ABCD,点E在BC上,点F在DC上,且∠EAF=45°,则有BE+DF= .若AB=4,则△CEF的周长为 .
(2)如图2,四边形ABCD中,∠BAD=∠C=90°,AB=AD,点E,F分别在BC,CD上,且∠EAF=45°,试判断BE,EF,DF之间的数量关系,并说明理由.
27.如图,正方形ABCD边长为8,E,F分别是BC,CD上的点,且AE⊥BF.
(1)求证:AE=BF.
(2)若AF=10,求AE的长.
28.正方形ABCD中,点E是BD上一点,过点E作EF⊥AE交射线CB于点F,连结CE.
(1)已知点F在线段BC上
①若AB=BE,求∠DAE度数;
②求证:CE=EF
(2)已知正方形边长为2,且BC=2BF,请直接写出线段DE的长.
答案
一.解答题
1.(1)∵四边形ABCD是正方形,
∴∠EBA=∠BAD=90°,
∴∠EAB=90°﹣∠BAE=90°﹣55°=35°,
∴∠HAD=∠BAD﹣∠EAF﹣∠EAB=90°﹣45°﹣35°=10°;
(2)∵四边形ABCD是正方形,
∴∠EBA=∠BAD=∠ADF=90°,
∴∠EAB=90°﹣∠BAE=90°﹣α,
∴∠DAF=∠BAD﹣∠EAF﹣∠EAB=90°﹣45°﹣(90°﹣α)=α﹣45°,
∴∠DFA=90°﹣∠DAF=90°﹣(α﹣45°)=135°﹣α;
(3)∠BEA=∠FEA,理由如下:
延长CB至I,使BI=DF,连接AI.
∵四边形ABCD是正方形,
∴AD=AB,∠ADF=∠ABC=90°,
∴∠ABI=90°,
又∵BI=DF,
∴△DAF≌△BAI(SAS),
∴AF=AI,∠DAF=∠BAI,
∴∠EAI=∠BAI+∠BAE=∠DAF+∠BAE=45°=∠EAF,
又∵AE是△EAI与△EAF的公共边,
∴△EAI≌△EAF(SAS),
∴∠BEA=∠FEA.
2.(1)证明:∵正方形ABCD的对角线AC,BD相交于点O,
∴OA=OC,OB=OD,
AC⊥BD.
∵BE=DF,
∴OB+BE=OD+DF,即OE=OF.
∴四边形AECF是平行四边形.
∵AC⊥EF,
∴四边形AECF是菱形.
(2)∵四边形ABCD是正方形,
∴AOAC,BOBD,AC=BD,AC⊥BD,
∴AO=BO,∠AOB=90°.
在直角△AOB中,由勾股定理知:AB3,
∴AO=BO=3.
∴EO=OB+BE=6.
在△AOE中,∠AOE=90°,AE3.
∵四边形AECF是菱形,
∴AE=EC=CF=AF.
∴四边形AECF的周长=4AE=12.
∴四边形AECF的周长是12.
3.(1)如图1,∵l∥m∥n∥k,BE⊥l,
∴BE⊥k,BE⊥m,BE⊥n,
∴∠AEB=∠BFC=90°,BE=5,BF=2,
∴∠CBF+∠BCF=90°,
∵正方形ABCD为“线上四边形”,
∴AB=BC,∠ABC=90°,
∴∠ABE+∠CBF=90°,
∴∠ABE=∠BCF,
∴△ABE≌△BCF(AAS),
∴FC=BE=5,
∴BC;
(2)如图2,连接AC,
∵四边形ABCD是菱形,
∴AD=CD,
∵∠ADC=60°,
∴△ADC是等边三角形,
∴AD=AC,∠CAD=60°,
∵△AEF是等边三角形,
∴AE=AF,∠EAF=60°,
∴∠EAF=∠CAD,
∴∠EAC=∠DAF,
∴△EAC≌△FAD(SAS),
∴EC=DF.
4.证明:(1)如图1,过E作MN∥AB,交AD于M,交BC于N,
∵四边形ABCD是正方形,
∴AD∥BC,AB⊥AD,
∴MN⊥AD,MN⊥BC,
∴∠AME=∠FNE=90°=∠NFE+∠FEN,
∵AE⊥EF,
∴∠AEF=∠AEM+∠FEN=90°,
∴∠AEM=∠NFE,
∵∠DBC=45°,∠BNE=90°,
∴BN=EN=AM,
∴△AEM≌△EFN(AAS),
∴AE=EF,
∵四边形ABCD是正方形,
∴AD=CD,∠ADE=∠CDE,
∵DE=DE,
∴△ADE≌△CDE(SAS),
∴AE=CE,
∴CE=EF;
5.(1)如图1,以直线BD为x轴,直线AC为y轴,建立平面直角坐标系,
∵四边形ABCD是正方形,
∴OA=OB=OC=OD,
∵点B(﹣1,0),A(0,1),
∴D(1,0),C(0,﹣1);
过N作NH⊥BD于h,
∴∠NHB=90°,
∵将BM绕点B逆时针旋转60°得到BN,
∴∠NBH=60°,BM=BN,
∴NHBNt,
∵0<t≤2,
∴点N纵坐标n的取值范围是0<n;
故答案为:(1,0),(0,﹣1);0<n;
(2)如图所示,连接MN,过E作EH⊥BC,交CB的延长线于H,
由旋转可得,BM=BN,∠NBM=60°,
∴△BMN是等边三角形,
∴MN=BM,
∵△ABE是等边三角形,
∴BE=BA,∠ABE=60°,
∴∠ABM=∠EBN,
∴△ABM≌△EBN(SAS),
∴AM=EN,
∴AM+BM+CM=EN+MN+CM,
∴当E,N,M,C在同一直线上时,AM+BM+CN的最小值是CE的长,
又∵∠ABE=60°,∠ABH=90°,
∴∠EBH=30°,
∴Rt△EBH中,EHEB2=1,
∴BH,
∴CH=2,
∴Rt△CEH中,CE;
∴AM+BM+CM的最小值为.
6.(1)解:BE+DF=EF;理由如下:
如图1,延长FD到G,使DG=BE,连接AG,
∵在△GDA和△EBA中,
,
∴△GDA≌△EBA(SAS),
∴AG=AE,∠GAD=∠EAB,
故∠GAF=45°,
在△GAF和△EAF中,
∵,
∴△GAF≌△EAF(SAS),
∴GF=EF,
即GD+DF=BE+DF=EF;
(2)AH=AB,理由如下:
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴把△ADF绕点A顺时针旋转90°得到△ABQ,如图2,
∴AQ=AF,∠FAQ=90°,∠ABQ=∠D=90°,
而∠ABC=90°,
∴点Q在CB的延长线上,
∵∠EAF=45°,
∴∠QAE=90°﹣∠EAF=45°,
∴∠EAF=∠QAE,
在△AEQ和△AEF中,
,
∴△AEQ≌△AEF(SAS),
∴EQ=EF,
∵AB⊥EQ,AH⊥FE,
∴AB=AH.
7.(1)证明:如图1,设正方形ABCD的边长为a.
将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.
则△ADF≌△ABG,DF=BG.
∴AF=AG,∠FAG=90°,
∵∠EAF=45°,
∴∠GAE=45°,
在△AGE与△AFE中,
,
∴△AGE≌△AFE(SAS);
∴EG=EF.
∵∠CEF=45°,
∴△BME、△DNF、△CEF均为等腰直角三角形,
∴CE=CF,BE=BM,NFDF,
∴a﹣BE=a﹣DF,
∴BE=DF,
∴BE=BM=DF=BG,
∴∠BMG=45°,
∴∠GME=45°+45°=90°,
∴EG2=ME2+MG2,
∵EG=EF,MGBMDF=NF,
∴EF2=ME2+NF2;
(2)解:EF2=2BE2+2DF2.
如图2所示,延长EF交AB延长线于M点,交AD延长线于N点,
将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.
由(1)知△AEH≌△AEF,
则由勾股定理有(GH+BE)2+BG2=EH2,
即(GH+BE)2+(BM﹣GM)2=EH2
又∴EF=HE,DF=GH=GM,BE=BM,所以有(GH+BE)2+(BE﹣GH)2=EF2,
即2(DF2+BE2)=EF2,
8.(1)证明:∵四边形CEFG是正方形,
∴CE=EF,
∵∠FEC=∠FEH+∠CED=90°,∠DCE+∠CED=90°,
∴∠FEH=∠DCE,
在△FEH和△ECD中,
∴△FEH≌△ECD(AAS),
∴FH=ED;
(2)解:∵在矩形ABCD中,AB=3,AD=5,
∴CD=AB=3,
∵AE=1,
∴DE=4,
∵△FEH≌△ECD,
∴FH=DE=4,EH=CD=3,
∴AH=4,
∴AH=FH,
∵∠FHE=90°,
∴∠FAD=45°.
9.(1)∵ME⊥AO,MF⊥BO,
∴∠MEO=90°,∠MFO=90°,
∵正方形ABCD的对角线AC,BD交于点O,
∴∠EOF=90°,
∴四边形OEMF为矩形;
(2)∵边长为8的正方形ABCD的对角线AC,BD交于点O,
∴OA=OB=4,
当M在AB的中点时,EF有最小值,最小值.
10.证明:(1)∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠C=∠ADC=∠DAB=90°,
如图①:延长BA,使AM=CF,连接MD,
在△AMD和△CFD中,
,
∴△AMD≌△CFD(SAS),
∴∠MDA=∠CDF,MD=DF,
∵∠EDF=45°,
∴∠ADE+∠FDC=45°,
∴∠ADM+∠ADE=45°=∠MDE,
∴∠MDE=∠EDF,
在△EDF和△EDM中,
,
∴△EDF≌△EDM(SAS),
∴EF=EM,
∵EM=AM+AE=AE+CF,
∴EF=AE+CF;
(2)EF2=AE2+CF2,
理由如下:
如图②,将△CDF绕点D顺时针旋转90°,可得△ADN,
由旋转的性质可得DN=DF,AN=CF,∠DAN=∠DCF=45°,∠CDF=∠ADN,
∴∠CAN=∠CAD+∠DAN=90°,
∴EN2=AE2+AN2,
∵∠EDF=45°,
∴∠CDF+∠ADE=45°,
∴∠ADE+∠ADN=45°=∠NDE=∠EDF,
在△EDF和△EDN中,
,
∴△EDF≌△EDN(SAS),
∴EF=EN,
∴EF2=AE2+CF2.
11.证明:∵四边形ABCD是正方形,
∴AB=AD,∠B=∠ADC=90°,
∴∠ADF=90°,
∴∠B=∠ADF,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(SAS).
12.证明:(1)如图1:把△ABE绕点A逆时针旋转90°至△ADG,
则△ADG≌△ABE,
∴AG=AE,∠DAG=∠BAE,DG=BE,
又∵∠EAF=45°,即∠DAF+∠BEA=∠EAF=45°,
∴∠GAF=∠FAE,
在△GAF和△EAF中,
,
∴△GAF≌△EAF(SAS).
∴GF=EF.
又∵DG=BE,
∴GF=BE+DF,
∴BE+DF=EF;
(2)当∠BAD=2∠EAF时,仍有EF=BE+FD,
理由如下:如图2,延长CB至M,使BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,
∴∠D=∠ABM,
在△ABM和△ADF中,
,
∴△ABM≌△ADF(SAS)
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=2∠EAF,
∴∠DAF+∠BAE=∠EAF,
∴∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,
,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE+BM=BE+DF,
即EF=BE+DF.
13.(1)结论:AG2=GE2+GF2.
理由:连接CG.
∵四边形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形EGFC是矩形,
∴CF=GE,
在Rt△GFC中,∵CG2=GF2+CF2,
∴AG2=GF2+GE2;
(2)过点A作AH⊥BG于H,
∵四边形ABCD是正方形,
∴∠ABD=∠GBF=45°,
∵GF⊥BC,
∴∠BGF=45°,
∵∠BAG=75°,
∴∠AGB=180°﹣∠ABD﹣∠BAG=60°,
∴∠GAH=30°,
在Rt△ABH中,∵AB,
∴AH2=BH23,
∴AH=BH,
在Rt△AGH中,∵AH,∠GAH=30°,
∴AG=2HG,
∵AG2=HG2+AH2,
∴(2HG)2=HG2+()2,
解得:HG=1,
∴BG=BH+HG1.
14.(1)解:设CE=x,则FG=EF=x,FH=6+x,
∵S正方形CEFG=S矩形ADEH,
∴S正方形CEFG+S矩形BCEH=S矩形BCEH+S矩形ADEH,
即S矩形BGFE=S正方形ABCD,
∴x(x+6)=36,解得x1=33,x2=﹣33(舍去),
即CE的长为33;
(2)证明:∵点M为BC边的中点,
∴MC=3,
在Rt△MCD中,DM3,
∵MG=MC+CG=3+33=3,
∴MD=MG.
15.(1)证明:∵四边形ABCD是正方形,
∴AD=DC,∠GAD=∠DCE=90°,
在△GAD和△ECD中,
,
∴△GAD≌△ECD(SAS),
∴DE=DG,∠GDA=∠EDC,
∴∠GDA+∠ADF=∠EDC+∠ADF,
即∠GDF=∠ADC=90°,
∵DE⊥CH,
∴∠DFH=∠CFD=90°,
∴DG∥CH,
∵∠HCB+∠HCD=∠EDC+∠DCF=90°,
∴∠HCB=∠EDC,
在△HBC和△ECD中,
,
∴△HBC≌△ECD(ASA)
∴CH=DE,
∴DG=CH,
∵DG∥CH,
∴四边形GHCD为平行四边形;
(2)∵△HBC≌△ECD,
∴∠BHC=∠CED,
∵∠ECF+∠FEC=90°,
∴∠FEC,∠BHC与∠ECF互余;
∵AD∥BC,
∴∠ADE=∠DEC,
∴∠ADE与∠ECF互余;
∵∠DGA=∠CHB,
∴∠DGA与∠ECF互余;
∵∠DCF+∠ECF=90°,
∴∠DCF与∠ECF互余;
∴与∠ECF互余的角有:∠FEC、∠DCF、∠BHC、∠DGA、∠ADE.
16.(1)证明:在正方形ABCD中,AD=DC,∠ADP=∠CDP=45°,
在△ADP和△CDP中
,
∴△ADP≌△CDP(SAS),
∴PA=PC,
∵∠PAE=∠E,
∴PA=PE,
∴PC=PE;
(2)∵在正方形ABCD中,∠ADC=90°,
∴∠EDF=90°,
由(1)知,△ADP≌△CDP,
∴∠DAP=∠DCP,
∵∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=90°.
17.(1)DP=EF,且DP⊥EF,理由是:
如图1所示:连接PB,
∵四边形ABCD是正方形,
∴BC=DC,∠BCP=∠DCP=45°,
∵在△CBP和△CDP中,
,
∴△CBP≌△CDP(SAS),
∴DP=BP,
∵PE⊥AB,PF⊥BC,
∴∠PEB=∠ABC=∠PFB=90°,
∴四边形BFPE是矩形,
∴BP=EF,
∴DP=EF;
如图2所示:延长DP交EF于G,延长EP交CD于H,连接PB.
∵△CBP≌△CDP,
∴∠CDP=∠CBP,
∵四边形BFPE是矩形,
∴∠CBP=∠FEP,
∴∠CDP=∠FEP,
又∵∠EPG=∠DPH,
∴∠EGP=∠DHP,
∵PE⊥AB,AB∥DC,
∴PH⊥DC.即∠DHP=90°,
∴∠EGP=∠DHP=90°,
∴PG⊥EF,即DP⊥EF;
(2)Rt△ADC中,AD=CD=6,
∴AC6,
∵∠ADP:∠PDC=1:3,∠ADC=90°,
∴∠CDP=67.5°,
∵∠DCP=45°,
∴∠CPD=180°﹣45°﹣67.5°=67.5°,
∴∠CPD=∠CDP,
∴PC=CD=6,
∴AP=66,
∵∠EAP=45°,∠AEP=90°,
∴△AEP是等腰直角三角形,
∴PE6﹣3.
18.(1)证明:∵四边形ABCD是正方形,
∴OA=OB,∠DAO=45°,∠OBA=45°,
∴∠OAM=∠OBN=135°,
∵∠EOF=90°,∠AOB=90°,
∴∠AOM=∠BON,
在△OAM和△OBN中,
∴△OAM≌△OBN(ASA),
∴OM=ON;
(2)如图,过点O作OH⊥AD于点H,
∵正方形的边长为8,
∴OH=HA=4,
∵E为OM的中点,
∴HM=8,
则OM4,
∴MNOM=4.
19.(1)EG=BE+DG.
如图1,延长AD至F,使DF=BE,连接CF,
∵四边形ABCD为正方形,
∴BC=DC,∠ABC=∠ADC=∠BCD=90°,
∵∠CDF=180﹣∠ADC,
∴∠CDF=90°,
∴∠ABC=∠CDF,
∵BE=DF,
∴△EBC≌△FDC(SAS),
∴∠BCE=∠DCF,EC=FC,
∵∠ECG=45°,
∴∠BCE+∠GCD=∠BCD﹣∠ECG=90°﹣45°=45°,
∴∠GCD+DCF=∠FCG=45°,
∴∠ECG=∠FCG,
∵GC=GC,
∴△ECG≌△FCG(SAS),
∴EG=GF,
∵GF=GD+DF=GD+BE,
∴EG=GD+BE.
(2)如图2,过点C作CD⊥AG,交AG的延长线于D.
∵AG∥BC,
∴∠A+∠B=180°,
∵∠B=90°,
∴∠A=180°﹣∠B=90°,
∵∠CDA=90°,AB=BC,
∴四边形ABCD是正方形,
∵AB=BC=12,
∴CD=AD=12,
∵BE=4,
∴AE=AB﹣BE=8,
设EG=x,由(1)知EG=BE+GD,
∴GD=x﹣4,
∴AG=AD﹣GD=12﹣(x﹣4)=16﹣x,
在Rt△AEG中:GE2=AG2+AE2,
∴x2=(16﹣x)2+82,解得x=10,
∴EG=10.
20.解:(1)∵四边形ABCD是正方形,
∴AD=AB=2,BDAD=2,∠ABD=∠CBD=45°,
∴BE=BD﹣DE=21,
∵EG⊥BD,∠DBG=45°,
∴∠DBG=∠EGB=45°,
∴EB=EG=21;
(2)∵AE⊥EF,
∴∠AEF=∠BEG=90°,
∴∠AEB=∠GEF,
又∵BE=EG,∠ABD=∠FGE=45°,
∴△ABE≌△FGE(AAS),
∴FG=AB.
21.证明:(1)四边形APQD是平行四边形,理由是:
∵四边形ABCD为正方形,
∴AD=BC,AD∥BC,
由平移得:BC=PQ,
∴AD∥PQ,AD=PQ,
∴四边形APQD是平行四边形;
(2)OA⊥OP,OA=OP,理由是:
∵四边形ABCD为正方形,
∴∠ABO=∠OBC=45°,
∵OQ⊥BD,
∴∠BOQ=90°,
∴∠OQB=45°,
∴∠OQB=∠ABO=∠OBQ=45°,
∴OB=OQ,
在△ABO和△PQO中,
∵,
∴△ABO≌△PQO(SAS),
∴OA=OP,∠AOB=∠POQ,
∵∠BOQ=∠BOP+∠POQ=90°,
∴∠BOP+∠AOB=∠AOP=90°,
∴OA⊥OP.
22.(1)CF+BC=CD.理由如下:
∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°﹣∠DAC,∠CAF=90°﹣∠DAC,
∴∠BAD=∠CAF,
在△ABD和△ACF中,
,
∴△ABD≌△ACF(SAS),
∴BD=CF,
∵BD+BC=CD,
∴CF+BC=CD;
(2)∵△ABD≌△ACF,
∴∠ACF=∠ABD,
∵∠ABC=45°,
∴∠ABD=135°,
∴∠ACF=∠ABD=135°,
∴∠FCD=90°,
∴△FCD是直角三角形.
∵正方形ADEF的边长为2,且对角线AE、DF相交于点O.
∴DFAD=4,O为DF中点.
∴OCDF=2.
23.证明:(1)∵四边形ABCD是正方形,
∴AC⊥BD,AO=BO=CO=DO,
∵AQ⊥BR,
∴∠AQR=∠AOP=90°,
∴∠QAR+∠ARQ=90°,∠PAO+∠APO=90°,
∴∠APO=∠ARQ,
∴△AOP≌△BOR(AAS),
∴OP=OR;
(2)∵四边形ABCD是正方形,
∴AC⊥BD,AO=BO=CO=DO,
∵AQ⊥BR,
∴∠AQR=∠AOP=90°,
∴∠QAR+∠ARQ=90°,∠PAO+∠APO=90°,
∴∠APO=∠ARQ,
∴△AOP≌△BOR(AAS),
∴OP=OR;
∴AO+OR=DO+OP,
∴AR=DP,
故答案为:AR=DP.
24.(1)如图1,过点E作EF⊥AM于点F,连接EM,
∵四边形ABCD是正方形,
∴∠D=∠C=90°,
∴∠D=∠AFE,
∵AE平分∠DAM,
∴∠DAE=∠FAE,
AE=AE,
∴△ADE≌△AFE(AAS),
∴AD=AF,DE=FE,
∵E是CD边的中点,
∴DE=EC,
∴FE=EC,
EM=EM,
∴Rt△EFM≌Rt△ECM(HL),
∴FM=MC.
∴AM=AF+FM=AD+MC.
(2)AM=AD+MC成立,理由如下:
如图2,过点E作EF⊥AM于点F,连接EM,
∵四边形ABCD是矩形,
∴∠D=∠C=90°,
∴∠D=∠AFE,
∵AE平分∠DAM,
∴∠DAE=∠FAE,
AE=AE,
∴△ADE≌△AFE(AAS),
∴AD=AF,DE=FE,
∵E是CD边的中点,
∴DE=EC,
∴FE=EC,
EM=EM,
∴Rt△EFM≌Rt△ECM(HL),
∴FM=MC.
∴AM=AF+FM=AD+MC.
所以AM=AD+MC成立.
25.过点E作EG⊥BC,交BC的延长线于点G.
∵BD∥EF,
∴∠ECG=∠DBC=45°,
∴△ECG是等腰直角三角形,
∴EG=CG,
设EG=x,则BG=2+x,
在Rt△BEG中,BE2=BG2+EG2,
即(2)2=(2+x)2+x2,
即x2+2x﹣2=0,
解得:x1或x1(舍去),
∴EG1,
∴CEEG.
26.(1)延长EB至H,使BH=DF,连接AH,如图1,
∵在正方形ABCD中,
∴∠ADF=∠ABH,AD=AB,
在△ADF和△ABH中,,
∴△ADF≌△ABH(SAS),
∴∠BAH=∠DAF,AF=AH,
∴∠FAH=90°,
∴∠EAF=∠EAH=45°,
在△FAE和△HAE中,,
∴△FAE≌△HAE(SAS),
∴EF=HE=BE+HB,
∴EF=BE+DF,
∴△CEF的周长=EF+CE+CF=BE+CE+DF+CF=BC+CD=2AB=8.
故答案为:EF;8.
(2)EF=BE+DF,理由如下:
延长CB至M,使BM=DF,连接AM,如图2,
∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,
∴∠D=∠ABM,
在△ABM和△ADF中,,
∴△ABM≌△ADF(SAS),
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=∠C=90°,∠EAF=45°,
即∠BAD=2∠EAF,
∴∠DAF+∠BAE=∠EAF,
∴∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE+BM=BE+DF,
即EF=BE+DF.
27.证明;(1)∵四边形ABCD是正方形,
∴∠ABC=90°=∠C,AB=BC,
∴∠ABF+∠CBF=90°,
∵AE⊥BF,
∴∠ABF+∠BAE=90°,
∴∠BAE=∠CBF,
∴△ABE≌△BCF(ASA),
∴AE=BF;
(2)∵AF=10,AD=8,
∴DF6,
∴CF=8﹣6=2,
∴BF2,
∴AE=2.
28.解:(1)①∵ABCD为正方形,
∴∠ABE=45°.
又∵AB=BE,
∴∠BAE(180°﹣45°)=67.5°.
∴∠DAE=90°﹣67.5°=22.5°
②证明:∵正方形ABCD关于BD对称,
∴△ABE≌△CBE,
∴∠BAE=∠BCE.
又∵∠ABC=∠AEF=90°,
∴∠BAE=∠EFC,
∴∠BCE=∠EFC,
∴CE=EF.
(2)如下图所示:过点E作MN⊥BC,垂足为N,交AD于M.
∵CE=EF,
∴N是CF的中点.
∵BC=2BF,
∴.
又∵四边形CDMN是矩形,△DME为等腰直角三角形,
∴CN=DM=ME,
∴EDDMCN.
如下图所示:过点E作MN⊥BC,垂足为N,交AD于M.
∵正方形ABCD关于BD对称,
∴△ABE≌△CBE,
∴∠BAE=∠BCE.
又∵∠ABF=∠AEF=90°,
∴∠BAE=∠EFC,
∴∠BCE=∠EFC,
∴CE=EF.
∴FN=CN.
又∵BC=2BF,
∴FC=3,
∴CN,
∴EN=BN,
∴DE.
综上所述,ED的长为或
一.解答题
1.如图,四边形ABCD是正方形,点E是BC边上的动点(不与点B、C重合),将射线AE绕点A按逆时针方向旋转45°后交CD边于点F,AE、AF分别交BD于G、H两点.
(1)当∠BEA=55°时,求∠HAD的度数;
(2)设∠BEA=α,试用含α的代数式表示∠DFA的大小;
(3)点E运动的过程中,试探究∠BEA与∠FEA有怎样的数量关系,并说明理由.
2.如图,正方形ABCD的对角线AC、BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
(1)判断四边形AECF的形状,并证明你的猜想;
(2)若AB=3,BE=3,求四边形AECF的周长.
3.已知:l∥m∥n∥k,平行线l与m、m与n、n与k之间的距离分别为d1,d2,d3,且d1=d3=2,d2=3.我们把四个顶点分别在l,m,n,k这四条平行线上的四边形称为“线上四边形”.
(1)如图1,正方形ABCD为“线上四边形”,BE⊥l于点E,EB的延长线交直线k于点F,求正方形ABCD的边长.
(2)如图2,菱形ABCD为“线上四边形”且∠ADC=60°,△AEF是等边三角形,点E在直线k上,连接DF,且直线DF分别交直线l、k于点G、M,求证:EC=DF.
4.如图,在正方形ABCD中,AB=5cm,E为对角线BD上一动点,连接AE、CE,过E点作EF⊥AE,交直线BC于点F,E点从B点出发,沿BD方向以每秒1cm的速度运动,当点E与点D重合时,运动停止.设△BEF的面积为ycm2,E点的运动时间为x秒.
点E在整个运动过程中,试说明总有:CE=EF;
5.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.设点N的坐标为(m,n).
(1)若建立平面直角坐标系,满足原点在线段BD上,点B(﹣1,0),A(0,1).且BM=t(0<t≤2),则点D的坐标为 ,点C的坐标为 ;请直接写出点N纵坐标n的取值范围是 ;
(2)若正方形的边长为2,求EC的长,以及AM+BM+CM的最小值.
(提示:连结MN:1,1)
6.如图,在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°.
(1)如图(1),试判断EF,BE,DF间的数量关系,并说明理由;
(2)如图(2),若AH⊥EF于点H,试判断线段AH与AB的数量关系,并说明理由.
7.如图1,在正方形ABCD中,点E、F分别在边BC、CD上,且∠EAF=∠CEF=45°.
(1)若直线EF与AB、AD的延长线分别交于点M、N,求证:EF2=ME2+NF2;
(2)如图2,将正方形改为矩形,若其余条件不变,请写出线段EF、BE、DF之间的数量关系,并说明理由.
8.如图,在矩形ABCD中,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,垂足为H,连接AF.
(1)求证:FH=ED;
(2)若AB=3,AD=5,当AE=1时,求∠FAD的度数.
9.如图,边长为8的正方形ABCD的对角线AC,BD交于点O,M是AB边上一动点,ME⊥AO,MF⊥BO.
(1)求证:四边形OEMF为矩形;
(2)连接EF,求EF的最小值.
10.(1)如图①,点E、F分别在正方形ABCD的边AB、BC上,∠EDF=45°,连接EF,求证:EF=AE+FC.
(2)如图②,点E,F在正方形ABCD的对角线AC上,∠EDF=45°,猜想EF、AE、FC的数量关系,并说明理由.
11.如图,在正方形ABCD中,点E是BC上的一点,点F是CD延长线上的一点,且BE=DF,连结AE、AF、EF.求证:△ABE≌△ADF.
12.(1)如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,求证:EF=BE+FD;
(2)如图2,四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足什么关系时,仍有EF=BE+FD,说明理由.
13.如图,在正方形ABCD中,点G在对角线BD上(不与点B,点D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG,
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由.
(2)若正方形ABCD的边长为,∠BAG=75°,求线段BG的长.
14.如图,已知正方形ABCD的边长为6,点E在CD边上,以线段CE为边长在正方形ABCD的外部作正方形CEFG,以线段AD和DE为邻边作矩形ADEH,若S正方形CEFG=S矩形ADEH.
(1)求线段CE的长;
(2)若点M为BC边的中点,连结MD,求证:MD=MG.
15.如图,四边形ABCD是正方形,点E,H分别在BC,AB上,点G在BA的延长线上,且CE=AG,DE⊥CH于F.
(1)求证:四边形GHCD为平行四边形.
(2)在不添加任何辅助线的情况下,请直接写出图中所有与∠ECF互余的角.
16.如图,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且∠PAE=∠E,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数.
17.如图,P为正方形ABCD的对角线上任一点,PE⊥AB于E,PF⊥BC于F.
(1)判断DP与EF的关系,并证明;
(2)若正方形ABCD的边长为6,∠ADP:∠PDC=1:3.求PE的长.
18.如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.
(1)求证:OM=ON.
(2)若正方形ABCD的边长为8,E为OM的中点,求MN的长.
19.(1)如图1,在正方形ABCD中,E是AB上一点,G是AD上一点,∠ECG=45°,那么EG与图中两条线段的和相等?证明你的结论.
(2)请用(1)中所积累的经验和知识完成此题,如图2,在四边形ABCD中,AG∥BC(BC>AG),∠B=90°,AB=BC=12,E是AB上一点,且∠ECG=45°,BE=4,求EG的长?
20.如图,在正方形ABCD中,点E是对角线BD上的一点(DE<BE),连接AE,过点E分别作EF⊥AE交BC于点F,EG⊥BD交BC的延长线于点G.
(1)若AD=2,DE=1,求EG的长度;
(2)求证:FG=AB.
21.如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,经通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明.
22.已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为射线CB上一点.以AD为边做正方形ADEF,连接CF,且点A,F分别在直线BC的两侧.
(1)请直接写出CF,BC,CD三条线段之间的关系;
(2)若正方形ADEF的边长为2,对角线AE,DF相交于点O,连接OC.求OC的长度.
23.如图1,在正方形ABCD中,对角线AC与BD相交于点O,R是AC上任意一点,连接BR,过点A作AQ⊥BR,垂足为点Q,AQ与BD交于点P.
(1)求证:OP=OR;
(2)如图2,若点R在AC的延长线上,AQ⊥BR于点Q,AQ与DB的延长线交于点P,其他条件不变,判断线段DP与AR的数量关系: .
24.四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(1)求证:AM=AD+MC.
(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,试判断AM=AD+MC是否成立?若成立,请给出证明,若不成立,请说明理由;
25.如图,正方形ABCD的边长为2.以对角线BD为边作菱形BEFD.点C,E,F在同一直线上,求CE的长.
26.(1)如图1,已知正方形ABCD,点E在BC上,点F在DC上,且∠EAF=45°,则有BE+DF= .若AB=4,则△CEF的周长为 .
(2)如图2,四边形ABCD中,∠BAD=∠C=90°,AB=AD,点E,F分别在BC,CD上,且∠EAF=45°,试判断BE,EF,DF之间的数量关系,并说明理由.
27.如图,正方形ABCD边长为8,E,F分别是BC,CD上的点,且AE⊥BF.
(1)求证:AE=BF.
(2)若AF=10,求AE的长.
28.正方形ABCD中,点E是BD上一点,过点E作EF⊥AE交射线CB于点F,连结CE.
(1)已知点F在线段BC上
①若AB=BE,求∠DAE度数;
②求证:CE=EF
(2)已知正方形边长为2,且BC=2BF,请直接写出线段DE的长.
答案
一.解答题
1.(1)∵四边形ABCD是正方形,
∴∠EBA=∠BAD=90°,
∴∠EAB=90°﹣∠BAE=90°﹣55°=35°,
∴∠HAD=∠BAD﹣∠EAF﹣∠EAB=90°﹣45°﹣35°=10°;
(2)∵四边形ABCD是正方形,
∴∠EBA=∠BAD=∠ADF=90°,
∴∠EAB=90°﹣∠BAE=90°﹣α,
∴∠DAF=∠BAD﹣∠EAF﹣∠EAB=90°﹣45°﹣(90°﹣α)=α﹣45°,
∴∠DFA=90°﹣∠DAF=90°﹣(α﹣45°)=135°﹣α;
(3)∠BEA=∠FEA,理由如下:
延长CB至I,使BI=DF,连接AI.
∵四边形ABCD是正方形,
∴AD=AB,∠ADF=∠ABC=90°,
∴∠ABI=90°,
又∵BI=DF,
∴△DAF≌△BAI(SAS),
∴AF=AI,∠DAF=∠BAI,
∴∠EAI=∠BAI+∠BAE=∠DAF+∠BAE=45°=∠EAF,
又∵AE是△EAI与△EAF的公共边,
∴△EAI≌△EAF(SAS),
∴∠BEA=∠FEA.
2.(1)证明:∵正方形ABCD的对角线AC,BD相交于点O,
∴OA=OC,OB=OD,
AC⊥BD.
∵BE=DF,
∴OB+BE=OD+DF,即OE=OF.
∴四边形AECF是平行四边形.
∵AC⊥EF,
∴四边形AECF是菱形.
(2)∵四边形ABCD是正方形,
∴AOAC,BOBD,AC=BD,AC⊥BD,
∴AO=BO,∠AOB=90°.
在直角△AOB中,由勾股定理知:AB3,
∴AO=BO=3.
∴EO=OB+BE=6.
在△AOE中,∠AOE=90°,AE3.
∵四边形AECF是菱形,
∴AE=EC=CF=AF.
∴四边形AECF的周长=4AE=12.
∴四边形AECF的周长是12.
3.(1)如图1,∵l∥m∥n∥k,BE⊥l,
∴BE⊥k,BE⊥m,BE⊥n,
∴∠AEB=∠BFC=90°,BE=5,BF=2,
∴∠CBF+∠BCF=90°,
∵正方形ABCD为“线上四边形”,
∴AB=BC,∠ABC=90°,
∴∠ABE+∠CBF=90°,
∴∠ABE=∠BCF,
∴△ABE≌△BCF(AAS),
∴FC=BE=5,
∴BC;
(2)如图2,连接AC,
∵四边形ABCD是菱形,
∴AD=CD,
∵∠ADC=60°,
∴△ADC是等边三角形,
∴AD=AC,∠CAD=60°,
∵△AEF是等边三角形,
∴AE=AF,∠EAF=60°,
∴∠EAF=∠CAD,
∴∠EAC=∠DAF,
∴△EAC≌△FAD(SAS),
∴EC=DF.
4.证明:(1)如图1,过E作MN∥AB,交AD于M,交BC于N,
∵四边形ABCD是正方形,
∴AD∥BC,AB⊥AD,
∴MN⊥AD,MN⊥BC,
∴∠AME=∠FNE=90°=∠NFE+∠FEN,
∵AE⊥EF,
∴∠AEF=∠AEM+∠FEN=90°,
∴∠AEM=∠NFE,
∵∠DBC=45°,∠BNE=90°,
∴BN=EN=AM,
∴△AEM≌△EFN(AAS),
∴AE=EF,
∵四边形ABCD是正方形,
∴AD=CD,∠ADE=∠CDE,
∵DE=DE,
∴△ADE≌△CDE(SAS),
∴AE=CE,
∴CE=EF;
5.(1)如图1,以直线BD为x轴,直线AC为y轴,建立平面直角坐标系,
∵四边形ABCD是正方形,
∴OA=OB=OC=OD,
∵点B(﹣1,0),A(0,1),
∴D(1,0),C(0,﹣1);
过N作NH⊥BD于h,
∴∠NHB=90°,
∵将BM绕点B逆时针旋转60°得到BN,
∴∠NBH=60°,BM=BN,
∴NHBNt,
∵0<t≤2,
∴点N纵坐标n的取值范围是0<n;
故答案为:(1,0),(0,﹣1);0<n;
(2)如图所示,连接MN,过E作EH⊥BC,交CB的延长线于H,
由旋转可得,BM=BN,∠NBM=60°,
∴△BMN是等边三角形,
∴MN=BM,
∵△ABE是等边三角形,
∴BE=BA,∠ABE=60°,
∴∠ABM=∠EBN,
∴△ABM≌△EBN(SAS),
∴AM=EN,
∴AM+BM+CM=EN+MN+CM,
∴当E,N,M,C在同一直线上时,AM+BM+CN的最小值是CE的长,
又∵∠ABE=60°,∠ABH=90°,
∴∠EBH=30°,
∴Rt△EBH中,EHEB2=1,
∴BH,
∴CH=2,
∴Rt△CEH中,CE;
∴AM+BM+CM的最小值为.
6.(1)解:BE+DF=EF;理由如下:
如图1,延长FD到G,使DG=BE,连接AG,
∵在△GDA和△EBA中,
,
∴△GDA≌△EBA(SAS),
∴AG=AE,∠GAD=∠EAB,
故∠GAF=45°,
在△GAF和△EAF中,
∵,
∴△GAF≌△EAF(SAS),
∴GF=EF,
即GD+DF=BE+DF=EF;
(2)AH=AB,理由如下:
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴把△ADF绕点A顺时针旋转90°得到△ABQ,如图2,
∴AQ=AF,∠FAQ=90°,∠ABQ=∠D=90°,
而∠ABC=90°,
∴点Q在CB的延长线上,
∵∠EAF=45°,
∴∠QAE=90°﹣∠EAF=45°,
∴∠EAF=∠QAE,
在△AEQ和△AEF中,
,
∴△AEQ≌△AEF(SAS),
∴EQ=EF,
∵AB⊥EQ,AH⊥FE,
∴AB=AH.
7.(1)证明:如图1,设正方形ABCD的边长为a.
将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.
则△ADF≌△ABG,DF=BG.
∴AF=AG,∠FAG=90°,
∵∠EAF=45°,
∴∠GAE=45°,
在△AGE与△AFE中,
,
∴△AGE≌△AFE(SAS);
∴EG=EF.
∵∠CEF=45°,
∴△BME、△DNF、△CEF均为等腰直角三角形,
∴CE=CF,BE=BM,NFDF,
∴a﹣BE=a﹣DF,
∴BE=DF,
∴BE=BM=DF=BG,
∴∠BMG=45°,
∴∠GME=45°+45°=90°,
∴EG2=ME2+MG2,
∵EG=EF,MGBMDF=NF,
∴EF2=ME2+NF2;
(2)解:EF2=2BE2+2DF2.
如图2所示,延长EF交AB延长线于M点,交AD延长线于N点,
将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.
由(1)知△AEH≌△AEF,
则由勾股定理有(GH+BE)2+BG2=EH2,
即(GH+BE)2+(BM﹣GM)2=EH2
又∴EF=HE,DF=GH=GM,BE=BM,所以有(GH+BE)2+(BE﹣GH)2=EF2,
即2(DF2+BE2)=EF2,
8.(1)证明:∵四边形CEFG是正方形,
∴CE=EF,
∵∠FEC=∠FEH+∠CED=90°,∠DCE+∠CED=90°,
∴∠FEH=∠DCE,
在△FEH和△ECD中,
∴△FEH≌△ECD(AAS),
∴FH=ED;
(2)解:∵在矩形ABCD中,AB=3,AD=5,
∴CD=AB=3,
∵AE=1,
∴DE=4,
∵△FEH≌△ECD,
∴FH=DE=4,EH=CD=3,
∴AH=4,
∴AH=FH,
∵∠FHE=90°,
∴∠FAD=45°.
9.(1)∵ME⊥AO,MF⊥BO,
∴∠MEO=90°,∠MFO=90°,
∵正方形ABCD的对角线AC,BD交于点O,
∴∠EOF=90°,
∴四边形OEMF为矩形;
(2)∵边长为8的正方形ABCD的对角线AC,BD交于点O,
∴OA=OB=4,
当M在AB的中点时,EF有最小值,最小值.
10.证明:(1)∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠C=∠ADC=∠DAB=90°,
如图①:延长BA,使AM=CF,连接MD,
在△AMD和△CFD中,
,
∴△AMD≌△CFD(SAS),
∴∠MDA=∠CDF,MD=DF,
∵∠EDF=45°,
∴∠ADE+∠FDC=45°,
∴∠ADM+∠ADE=45°=∠MDE,
∴∠MDE=∠EDF,
在△EDF和△EDM中,
,
∴△EDF≌△EDM(SAS),
∴EF=EM,
∵EM=AM+AE=AE+CF,
∴EF=AE+CF;
(2)EF2=AE2+CF2,
理由如下:
如图②,将△CDF绕点D顺时针旋转90°,可得△ADN,
由旋转的性质可得DN=DF,AN=CF,∠DAN=∠DCF=45°,∠CDF=∠ADN,
∴∠CAN=∠CAD+∠DAN=90°,
∴EN2=AE2+AN2,
∵∠EDF=45°,
∴∠CDF+∠ADE=45°,
∴∠ADE+∠ADN=45°=∠NDE=∠EDF,
在△EDF和△EDN中,
,
∴△EDF≌△EDN(SAS),
∴EF=EN,
∴EF2=AE2+CF2.
11.证明:∵四边形ABCD是正方形,
∴AB=AD,∠B=∠ADC=90°,
∴∠ADF=90°,
∴∠B=∠ADF,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(SAS).
12.证明:(1)如图1:把△ABE绕点A逆时针旋转90°至△ADG,
则△ADG≌△ABE,
∴AG=AE,∠DAG=∠BAE,DG=BE,
又∵∠EAF=45°,即∠DAF+∠BEA=∠EAF=45°,
∴∠GAF=∠FAE,
在△GAF和△EAF中,
,
∴△GAF≌△EAF(SAS).
∴GF=EF.
又∵DG=BE,
∴GF=BE+DF,
∴BE+DF=EF;
(2)当∠BAD=2∠EAF时,仍有EF=BE+FD,
理由如下:如图2,延长CB至M,使BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,
∴∠D=∠ABM,
在△ABM和△ADF中,
,
∴△ABM≌△ADF(SAS)
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=2∠EAF,
∴∠DAF+∠BAE=∠EAF,
∴∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,
,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE+BM=BE+DF,
即EF=BE+DF.
13.(1)结论:AG2=GE2+GF2.
理由:连接CG.
∵四边形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形EGFC是矩形,
∴CF=GE,
在Rt△GFC中,∵CG2=GF2+CF2,
∴AG2=GF2+GE2;
(2)过点A作AH⊥BG于H,
∵四边形ABCD是正方形,
∴∠ABD=∠GBF=45°,
∵GF⊥BC,
∴∠BGF=45°,
∵∠BAG=75°,
∴∠AGB=180°﹣∠ABD﹣∠BAG=60°,
∴∠GAH=30°,
在Rt△ABH中,∵AB,
∴AH2=BH23,
∴AH=BH,
在Rt△AGH中,∵AH,∠GAH=30°,
∴AG=2HG,
∵AG2=HG2+AH2,
∴(2HG)2=HG2+()2,
解得:HG=1,
∴BG=BH+HG1.
14.(1)解:设CE=x,则FG=EF=x,FH=6+x,
∵S正方形CEFG=S矩形ADEH,
∴S正方形CEFG+S矩形BCEH=S矩形BCEH+S矩形ADEH,
即S矩形BGFE=S正方形ABCD,
∴x(x+6)=36,解得x1=33,x2=﹣33(舍去),
即CE的长为33;
(2)证明:∵点M为BC边的中点,
∴MC=3,
在Rt△MCD中,DM3,
∵MG=MC+CG=3+33=3,
∴MD=MG.
15.(1)证明:∵四边形ABCD是正方形,
∴AD=DC,∠GAD=∠DCE=90°,
在△GAD和△ECD中,
,
∴△GAD≌△ECD(SAS),
∴DE=DG,∠GDA=∠EDC,
∴∠GDA+∠ADF=∠EDC+∠ADF,
即∠GDF=∠ADC=90°,
∵DE⊥CH,
∴∠DFH=∠CFD=90°,
∴DG∥CH,
∵∠HCB+∠HCD=∠EDC+∠DCF=90°,
∴∠HCB=∠EDC,
在△HBC和△ECD中,
,
∴△HBC≌△ECD(ASA)
∴CH=DE,
∴DG=CH,
∵DG∥CH,
∴四边形GHCD为平行四边形;
(2)∵△HBC≌△ECD,
∴∠BHC=∠CED,
∵∠ECF+∠FEC=90°,
∴∠FEC,∠BHC与∠ECF互余;
∵AD∥BC,
∴∠ADE=∠DEC,
∴∠ADE与∠ECF互余;
∵∠DGA=∠CHB,
∴∠DGA与∠ECF互余;
∵∠DCF+∠ECF=90°,
∴∠DCF与∠ECF互余;
∴与∠ECF互余的角有:∠FEC、∠DCF、∠BHC、∠DGA、∠ADE.
16.(1)证明:在正方形ABCD中,AD=DC,∠ADP=∠CDP=45°,
在△ADP和△CDP中
,
∴△ADP≌△CDP(SAS),
∴PA=PC,
∵∠PAE=∠E,
∴PA=PE,
∴PC=PE;
(2)∵在正方形ABCD中,∠ADC=90°,
∴∠EDF=90°,
由(1)知,△ADP≌△CDP,
∴∠DAP=∠DCP,
∵∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=90°.
17.(1)DP=EF,且DP⊥EF,理由是:
如图1所示:连接PB,
∵四边形ABCD是正方形,
∴BC=DC,∠BCP=∠DCP=45°,
∵在△CBP和△CDP中,
,
∴△CBP≌△CDP(SAS),
∴DP=BP,
∵PE⊥AB,PF⊥BC,
∴∠PEB=∠ABC=∠PFB=90°,
∴四边形BFPE是矩形,
∴BP=EF,
∴DP=EF;
如图2所示:延长DP交EF于G,延长EP交CD于H,连接PB.
∵△CBP≌△CDP,
∴∠CDP=∠CBP,
∵四边形BFPE是矩形,
∴∠CBP=∠FEP,
∴∠CDP=∠FEP,
又∵∠EPG=∠DPH,
∴∠EGP=∠DHP,
∵PE⊥AB,AB∥DC,
∴PH⊥DC.即∠DHP=90°,
∴∠EGP=∠DHP=90°,
∴PG⊥EF,即DP⊥EF;
(2)Rt△ADC中,AD=CD=6,
∴AC6,
∵∠ADP:∠PDC=1:3,∠ADC=90°,
∴∠CDP=67.5°,
∵∠DCP=45°,
∴∠CPD=180°﹣45°﹣67.5°=67.5°,
∴∠CPD=∠CDP,
∴PC=CD=6,
∴AP=66,
∵∠EAP=45°,∠AEP=90°,
∴△AEP是等腰直角三角形,
∴PE6﹣3.
18.(1)证明:∵四边形ABCD是正方形,
∴OA=OB,∠DAO=45°,∠OBA=45°,
∴∠OAM=∠OBN=135°,
∵∠EOF=90°,∠AOB=90°,
∴∠AOM=∠BON,
在△OAM和△OBN中,
∴△OAM≌△OBN(ASA),
∴OM=ON;
(2)如图,过点O作OH⊥AD于点H,
∵正方形的边长为8,
∴OH=HA=4,
∵E为OM的中点,
∴HM=8,
则OM4,
∴MNOM=4.
19.(1)EG=BE+DG.
如图1,延长AD至F,使DF=BE,连接CF,
∵四边形ABCD为正方形,
∴BC=DC,∠ABC=∠ADC=∠BCD=90°,
∵∠CDF=180﹣∠ADC,
∴∠CDF=90°,
∴∠ABC=∠CDF,
∵BE=DF,
∴△EBC≌△FDC(SAS),
∴∠BCE=∠DCF,EC=FC,
∵∠ECG=45°,
∴∠BCE+∠GCD=∠BCD﹣∠ECG=90°﹣45°=45°,
∴∠GCD+DCF=∠FCG=45°,
∴∠ECG=∠FCG,
∵GC=GC,
∴△ECG≌△FCG(SAS),
∴EG=GF,
∵GF=GD+DF=GD+BE,
∴EG=GD+BE.
(2)如图2,过点C作CD⊥AG,交AG的延长线于D.
∵AG∥BC,
∴∠A+∠B=180°,
∵∠B=90°,
∴∠A=180°﹣∠B=90°,
∵∠CDA=90°,AB=BC,
∴四边形ABCD是正方形,
∵AB=BC=12,
∴CD=AD=12,
∵BE=4,
∴AE=AB﹣BE=8,
设EG=x,由(1)知EG=BE+GD,
∴GD=x﹣4,
∴AG=AD﹣GD=12﹣(x﹣4)=16﹣x,
在Rt△AEG中:GE2=AG2+AE2,
∴x2=(16﹣x)2+82,解得x=10,
∴EG=10.
20.解:(1)∵四边形ABCD是正方形,
∴AD=AB=2,BDAD=2,∠ABD=∠CBD=45°,
∴BE=BD﹣DE=21,
∵EG⊥BD,∠DBG=45°,
∴∠DBG=∠EGB=45°,
∴EB=EG=21;
(2)∵AE⊥EF,
∴∠AEF=∠BEG=90°,
∴∠AEB=∠GEF,
又∵BE=EG,∠ABD=∠FGE=45°,
∴△ABE≌△FGE(AAS),
∴FG=AB.
21.证明:(1)四边形APQD是平行四边形,理由是:
∵四边形ABCD为正方形,
∴AD=BC,AD∥BC,
由平移得:BC=PQ,
∴AD∥PQ,AD=PQ,
∴四边形APQD是平行四边形;
(2)OA⊥OP,OA=OP,理由是:
∵四边形ABCD为正方形,
∴∠ABO=∠OBC=45°,
∵OQ⊥BD,
∴∠BOQ=90°,
∴∠OQB=45°,
∴∠OQB=∠ABO=∠OBQ=45°,
∴OB=OQ,
在△ABO和△PQO中,
∵,
∴△ABO≌△PQO(SAS),
∴OA=OP,∠AOB=∠POQ,
∵∠BOQ=∠BOP+∠POQ=90°,
∴∠BOP+∠AOB=∠AOP=90°,
∴OA⊥OP.
22.(1)CF+BC=CD.理由如下:
∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°﹣∠DAC,∠CAF=90°﹣∠DAC,
∴∠BAD=∠CAF,
在△ABD和△ACF中,
,
∴△ABD≌△ACF(SAS),
∴BD=CF,
∵BD+BC=CD,
∴CF+BC=CD;
(2)∵△ABD≌△ACF,
∴∠ACF=∠ABD,
∵∠ABC=45°,
∴∠ABD=135°,
∴∠ACF=∠ABD=135°,
∴∠FCD=90°,
∴△FCD是直角三角形.
∵正方形ADEF的边长为2,且对角线AE、DF相交于点O.
∴DFAD=4,O为DF中点.
∴OCDF=2.
23.证明:(1)∵四边形ABCD是正方形,
∴AC⊥BD,AO=BO=CO=DO,
∵AQ⊥BR,
∴∠AQR=∠AOP=90°,
∴∠QAR+∠ARQ=90°,∠PAO+∠APO=90°,
∴∠APO=∠ARQ,
∴△AOP≌△BOR(AAS),
∴OP=OR;
(2)∵四边形ABCD是正方形,
∴AC⊥BD,AO=BO=CO=DO,
∵AQ⊥BR,
∴∠AQR=∠AOP=90°,
∴∠QAR+∠ARQ=90°,∠PAO+∠APO=90°,
∴∠APO=∠ARQ,
∴△AOP≌△BOR(AAS),
∴OP=OR;
∴AO+OR=DO+OP,
∴AR=DP,
故答案为:AR=DP.
24.(1)如图1,过点E作EF⊥AM于点F,连接EM,
∵四边形ABCD是正方形,
∴∠D=∠C=90°,
∴∠D=∠AFE,
∵AE平分∠DAM,
∴∠DAE=∠FAE,
AE=AE,
∴△ADE≌△AFE(AAS),
∴AD=AF,DE=FE,
∵E是CD边的中点,
∴DE=EC,
∴FE=EC,
EM=EM,
∴Rt△EFM≌Rt△ECM(HL),
∴FM=MC.
∴AM=AF+FM=AD+MC.
(2)AM=AD+MC成立,理由如下:
如图2,过点E作EF⊥AM于点F,连接EM,
∵四边形ABCD是矩形,
∴∠D=∠C=90°,
∴∠D=∠AFE,
∵AE平分∠DAM,
∴∠DAE=∠FAE,
AE=AE,
∴△ADE≌△AFE(AAS),
∴AD=AF,DE=FE,
∵E是CD边的中点,
∴DE=EC,
∴FE=EC,
EM=EM,
∴Rt△EFM≌Rt△ECM(HL),
∴FM=MC.
∴AM=AF+FM=AD+MC.
所以AM=AD+MC成立.
25.过点E作EG⊥BC,交BC的延长线于点G.
∵BD∥EF,
∴∠ECG=∠DBC=45°,
∴△ECG是等腰直角三角形,
∴EG=CG,
设EG=x,则BG=2+x,
在Rt△BEG中,BE2=BG2+EG2,
即(2)2=(2+x)2+x2,
即x2+2x﹣2=0,
解得:x1或x1(舍去),
∴EG1,
∴CEEG.
26.(1)延长EB至H,使BH=DF,连接AH,如图1,
∵在正方形ABCD中,
∴∠ADF=∠ABH,AD=AB,
在△ADF和△ABH中,,
∴△ADF≌△ABH(SAS),
∴∠BAH=∠DAF,AF=AH,
∴∠FAH=90°,
∴∠EAF=∠EAH=45°,
在△FAE和△HAE中,,
∴△FAE≌△HAE(SAS),
∴EF=HE=BE+HB,
∴EF=BE+DF,
∴△CEF的周长=EF+CE+CF=BE+CE+DF+CF=BC+CD=2AB=8.
故答案为:EF;8.
(2)EF=BE+DF,理由如下:
延长CB至M,使BM=DF,连接AM,如图2,
∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,
∴∠D=∠ABM,
在△ABM和△ADF中,,
∴△ABM≌△ADF(SAS),
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=∠C=90°,∠EAF=45°,
即∠BAD=2∠EAF,
∴∠DAF+∠BAE=∠EAF,
∴∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE+BM=BE+DF,
即EF=BE+DF.
27.证明;(1)∵四边形ABCD是正方形,
∴∠ABC=90°=∠C,AB=BC,
∴∠ABF+∠CBF=90°,
∵AE⊥BF,
∴∠ABF+∠BAE=90°,
∴∠BAE=∠CBF,
∴△ABE≌△BCF(ASA),
∴AE=BF;
(2)∵AF=10,AD=8,
∴DF6,
∴CF=8﹣6=2,
∴BF2,
∴AE=2.
28.解:(1)①∵ABCD为正方形,
∴∠ABE=45°.
又∵AB=BE,
∴∠BAE(180°﹣45°)=67.5°.
∴∠DAE=90°﹣67.5°=22.5°
②证明:∵正方形ABCD关于BD对称,
∴△ABE≌△CBE,
∴∠BAE=∠BCE.
又∵∠ABC=∠AEF=90°,
∴∠BAE=∠EFC,
∴∠BCE=∠EFC,
∴CE=EF.
(2)如下图所示:过点E作MN⊥BC,垂足为N,交AD于M.
∵CE=EF,
∴N是CF的中点.
∵BC=2BF,
∴.
又∵四边形CDMN是矩形,△DME为等腰直角三角形,
∴CN=DM=ME,
∴EDDMCN.
如下图所示:过点E作MN⊥BC,垂足为N,交AD于M.
∵正方形ABCD关于BD对称,
∴△ABE≌△CBE,
∴∠BAE=∠BCE.
又∵∠ABF=∠AEF=90°,
∴∠BAE=∠EFC,
∴∠BCE=∠EFC,
∴CE=EF.
∴FN=CN.
又∵BC=2BF,
∴FC=3,
∴CN,
∴EN=BN,
∴DE.
综上所述,ED的长为或
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
