八年级数学下册试题 11.3用反比例函数解决问题 苏科版(含答案)
文档属性
| 名称 | 八年级数学下册试题 11.3用反比例函数解决问题 苏科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 116.2KB | ||
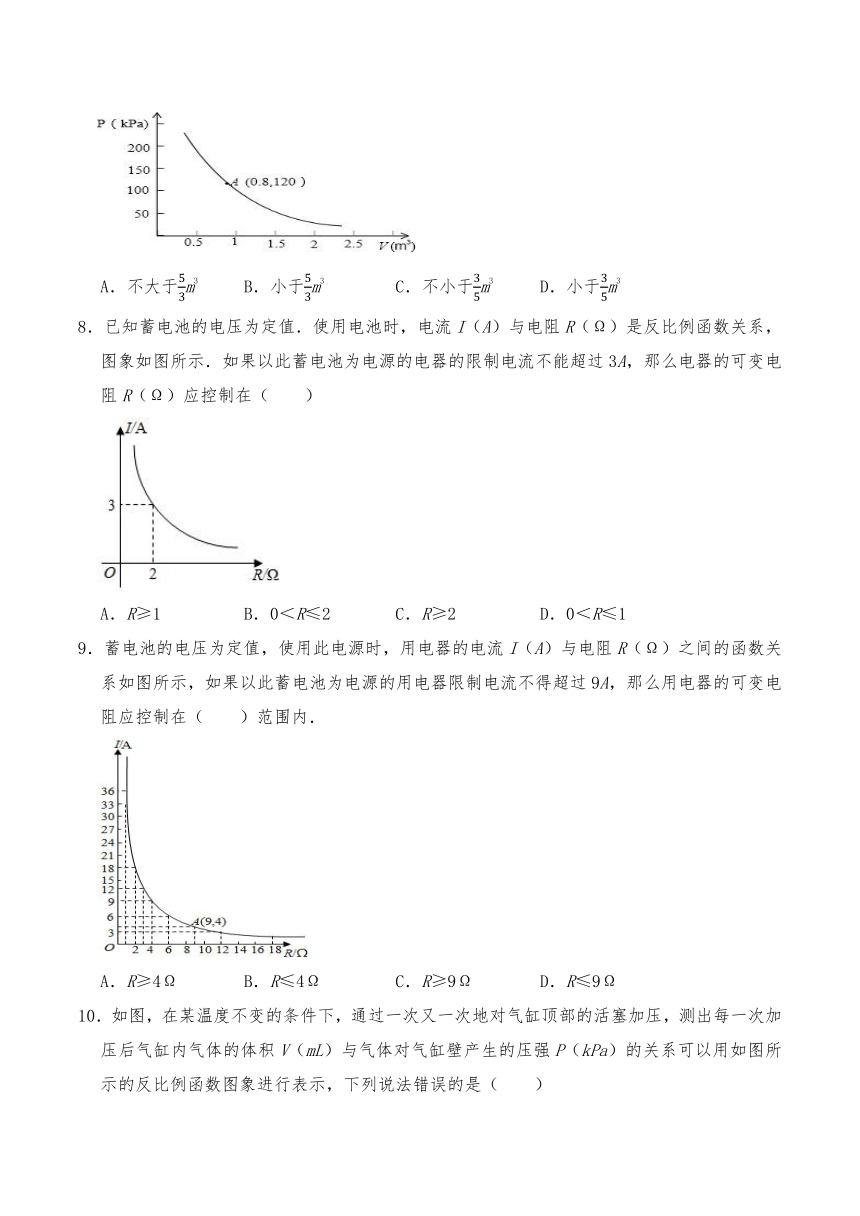
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-04 08:38:54 | ||
图片预览



文档简介
11.3用反比例函数解决问题
一、选择题.
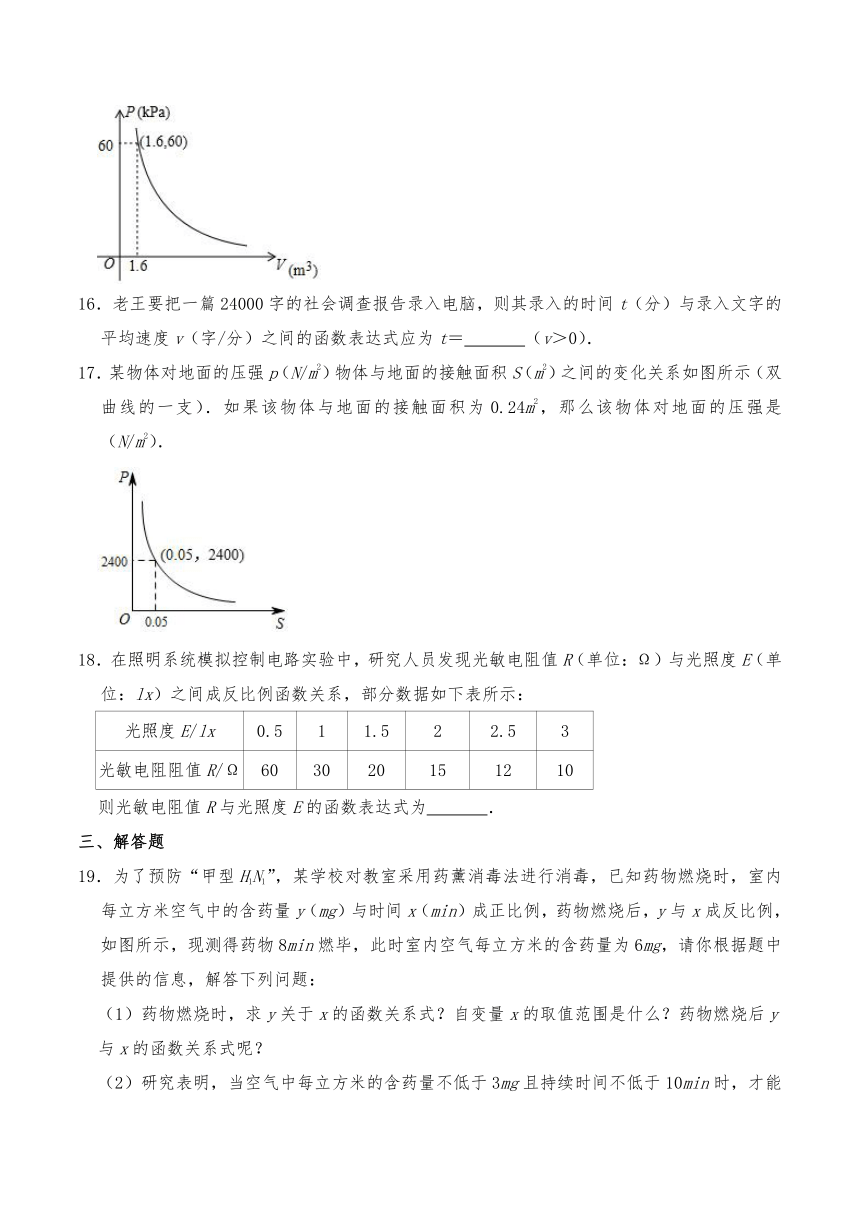
1.当压力F(N)一定时,物体所受的压强P(Pa)与受力面积S(m2)的函数关系式为P(S≠0),这个反比例函数的图象大致是( )
A. B.
C. D.
2.验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表,根据表中数据,可得y关于x的函数表达式为( )
近视眼镜的度数y(度) 200 250 400 500 1000
镜片焦距x(米) 0.50 0.40 0.25 0.20 0.10
A. B. C. D.
3.已知某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
A.不小于m3 B.小于m3 C.不小于m3 D.小于m3
4.1888年,海因里希 鲁道夫 赫兹证实了电磁波的存在,这成了后来大部分无线科技的基础.电磁波波长λ(单位:米)、频率f(单位:赫兹)满足函数关系λf=3×108,下列说法正确的是( )
A.电磁波波长是频率的正比例函数
B.电磁波波长20000米时,对应的频率1500赫兹
C.电磁波波长小于30000米时,频率小于10000赫兹
D.电磁波波长大于50000米时,频率小于6000赫兹
5.某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数,且当V=1.5m3时,p=16000Pa,当气球内的气压大于40000Pa时,气球将爆炸,为确保气球不爆炸,气球的体积应( )
A.不小于0.5m3 B.不大于0.5m3
C.不小于0.6m3 D.不大于0.6m3
6.当矩形面积一定时,下列图象中能表示它的长y和宽x之间函数关系的是( )
A. B.
C. D.
7.某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气球体积V的反比例函数,其图象如图所示,当气球内的气压大于160kPa时,气球将爆炸,为了安全,气球的体积应该( )
A.不大于m3 B.小于m3 C.不小于m3 D.小于m3
8.已知蓄电池的电压为定值.使用电池时,电流I(A)与电阻R(Ω)是反比例函数关系,图象如图所示.如果以此蓄电池为电源的电器的限制电流不能超过3A,那么电器的可变电阻R(Ω)应控制在( )
A.R≥1 B.0<R≤2 C.R≥2 D.0<R≤1
9.蓄电池的电压为定值,使用此电源时,用电器的电流I(A)与电阻R(Ω)之间的函数关系如图所示,如果以此蓄电池为电源的用电器限制电流不得超过9A,那么用电器的可变电阻应控制在( )范围内.
A.R≥4Ω B.R≤4Ω C.R≥9Ω D.R≤9Ω
10.如图,在某温度不变的条件下,通过一次又一次地对气缸顶部的活塞加压,测出每一次加压后气缸内气体的体积V(mL)与气体对气缸壁产生的压强P(kPa)的关系可以用如图所示的反比例函数图象进行表示,下列说法错误的是( )
A.气压P与体积V表达式为P,则k>0
B.当气压P=70时,体积V的取值范围为70<V<80
C.当体积V变为原来的时,对应的气压P变为原来的
D.当60≤V≤100时,气压P随着体积V的增大而减小
二、填空题
11.某厂计划建造一个容积为5×104m3的长方体蓄水池,则蓄水池的底面积S(m2)与其深度h(m)的函数关系式是 .
12.某高科技开发公司从2008年起开始投入技术改进资金,经过技术改进后,其产品的生产成本不断降低,具体数据如下表:请你认真分析表中数据,写出可以表示该变化规律的表达式是
年 度 2008 2009 2010 2011
投入技术改进资金x(万元) 2.5 3 4 4.5
产品成本y(万元∕件) 7.2 6 4.5 4
13.调查显示,某商场一款运动鞋的售价是销量的反比例函数(调查获得的部分数据如下表).
售价x(元/双) 200 240 250 400
销售量y(双) 30 25 24 15
已知该运动鞋的进价为180元/双,要使该款运动鞋每天的销售利润达到2400元,则其售价应定为 元.
14.面积一定的长方形,长为8时宽为5,当长为10时,宽为 .
15.某气球内充满了一定量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.则其函数解析式为 .
16.老王要把一篇24000字的社会调查报告录入电脑,则其录入的时间t(分)与录入文字的平均速度v(字/分)之间的函数表达式应为t= (v>0).
17.某物体对地面的压强p(N/m2)物体与地面的接触面积S(m2)之间的变化关系如图所示(双曲线的一支).如果该物体与地面的接触面积为0.24m2,那么该物体对地面的压强是 (N/m2).
18.在照明系统模拟控制电路实验中,研究人员发现光敏电阻值R(单位:Ω)与光照度E(单位:lx)之间成反比例函数关系,部分数据如下表所示:
光照度E/lx 0.5 1 1.5 2 2.5 3
光敏电阻阻值R/Ω 60 30 20 15 12 10
则光敏电阻值R与光照度E的函数表达式为 .
三、解答题
19.为了预防“甲型H1N1”,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
20.在压力不变的情况下,某物体所受到的压强p(Pa)与它的受力面积S(m2)之间成反比例函数关系,其图象如图所示.
(1)求p与S之间的函数表达式;
(2)当S=0.4m2时,求该物体所受到的压强p.
21.某种气球内充满了一定质量的气体.当温度不变时,气球内气体的压强P/(kPa)是气球体积V/(m3)的反比例函数,其图象如图所示.
(1)求这个反比例函数的表达式;
(2)当气球内气体的气压大于120 kPa时,气球将爆炸.为了安全起见,气球体积应该不小于多少立方米?
22.一辆货车和一辆轿车从南京出发,均沿沪宁高速公路匀速驶向目的地上海,已知沪宁高速公路全长约300km.设货车的速度是xkm/h,到达上海所用的时间为yh.
(1)写出y关于x的函数表达式;
(2)沪宁高速公路规定:货车的速度不得超过90km/h,求货车到达上海所需的最短时间;
(3)若轿车的速度是货车的1.5倍,轿车到达上海所用的时间比货车少1小时15分钟,求轿车的速度.
23.码头工人往一艘轮船上装载一批货物,每天装载30吨,8天装载完毕.
(1)轮船到达目的地后开始卸货,卸货速度v(吨/天)与卸货天数t之间有怎样的函数关系?
(2)由于遇到紧急情况,要求船上的货物5天之内卸载完毕,那么每天至少要卸货多少吨?
24.饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热,此过程中水温y(℃)与开机时间x(分)满足一次函数关系,当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系,当水温降至20℃时,饮水机又自动开始加热……,重复上述程序(如图所示),根据图中提供的信息,解答问题:
(1)当0≤x<8时,求水温y(℃)与开机时间x(分)的函数关系式.
(2)求图中t的值;
(3)若在通电开机后即外出散步,请你预测散步42分钟回到家时,饮水机内水的温度约为多少℃?
答案
一、选择题.
A.B.A.D.C.B.C.C.A.B.
二、填空题
11.S.
12.y.
13.300.
14.4.
15.P.
16..
17.500.
18.R.
三、解答题
19.(1)设药物燃烧时y关于x的函数关系式为y=k1x(k1>0),
代入(8,6)得6=8k1,
∴k1,
设药物燃烧后y关于x的函数关系式为y(k2>0),
代入(8,6)得
6,
∴k2=48,
∴药物燃烧时y关于x的函数关系式为(0≤x≤8)药物燃烧后y关于x的函数关系式为:
(x>8),
∴;
(2)把y=3代入,得:x=4,
把y=3代入,得:x=16,
∵16﹣4=12,
所以这次消毒是有效的.
20.(1)解:设 p(k≠0),
∵图象过点(0.1,1000)
∴1000
解得,k=100,
∴p与S之间的函数表达式是p;
(2)当S=0.4时,则 p250,
答:当S=0.4m2时,该物体所受到的压强p是250Pa.
21.(1)设P与V的函数关系式为P,
则60,
解得k=96,
∴函数关系式为P;
(2)当P>120KPa时,气球将爆炸,
∴P≤120,即120,
解得V≥0.8(m3).
故为了安全起见,气体的体积应不小于0.8(m3).
22.(1)设货车的速度是xkm/h,到达上海所用的时间为yh,根据题意可得:
xy=300,
故y;
(2)把x=90代入y,得y,
根据反比例函数的性质,当x>0时,y随x的增大而减小,
所以当x≤90km/h时,货车到达上海所需的最短时间为小时;
(3)根据题意可得:,
解方程得:x=80,
经检验得:x=80是原方程的解,且符合题意,
1.5x=120,
答:轿车的速度为120km/h.
23.(1)轮船上的货物总量为:30×8=240(吨),
故v关于t的函数表达式为v;
(2)把t=5代入v,得
v48,
∵t>0时,
∴v随t的增大而减小,
故船上的货物5天之内卸载完毕,每天至少要卸货48吨.
24.(1)当0≤x≤8时,设水温y(℃)与开机时间x(分)的函数关系式为y=kx+b(k≠0),
将(0,20)、(8,100)代入y=kx+b中,
,解得:,
∴当0≤x≤8时,水温y(℃)与开机时间x(分)的函数关系式为y=10x+20.
(2)当8≤x≤t时,设水温y(℃)与开机时间x(分)的函数关系式为y(m≠0),
将(8,100)代入y中,
100,解得:m=800,
∴当8≤x≤t时,水温y(℃)与开机时间x(分)的函数关系式为y.
当y20时,x=40,
∴图中t的值为40.
(3)∵42﹣40=2≤8,
∴当x=2时,y=2×10+20=40,
答:散步42分钟回到家时,饮水机内水的温度约为40℃.
一、选择题.
1.当压力F(N)一定时,物体所受的压强P(Pa)与受力面积S(m2)的函数关系式为P(S≠0),这个反比例函数的图象大致是( )
A. B.
C. D.
2.验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表,根据表中数据,可得y关于x的函数表达式为( )
近视眼镜的度数y(度) 200 250 400 500 1000
镜片焦距x(米) 0.50 0.40 0.25 0.20 0.10
A. B. C. D.
3.已知某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
A.不小于m3 B.小于m3 C.不小于m3 D.小于m3
4.1888年,海因里希 鲁道夫 赫兹证实了电磁波的存在,这成了后来大部分无线科技的基础.电磁波波长λ(单位:米)、频率f(单位:赫兹)满足函数关系λf=3×108,下列说法正确的是( )
A.电磁波波长是频率的正比例函数
B.电磁波波长20000米时,对应的频率1500赫兹
C.电磁波波长小于30000米时,频率小于10000赫兹
D.电磁波波长大于50000米时,频率小于6000赫兹
5.某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数,且当V=1.5m3时,p=16000Pa,当气球内的气压大于40000Pa时,气球将爆炸,为确保气球不爆炸,气球的体积应( )
A.不小于0.5m3 B.不大于0.5m3
C.不小于0.6m3 D.不大于0.6m3
6.当矩形面积一定时,下列图象中能表示它的长y和宽x之间函数关系的是( )
A. B.
C. D.
7.某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气球体积V的反比例函数,其图象如图所示,当气球内的气压大于160kPa时,气球将爆炸,为了安全,气球的体积应该( )
A.不大于m3 B.小于m3 C.不小于m3 D.小于m3
8.已知蓄电池的电压为定值.使用电池时,电流I(A)与电阻R(Ω)是反比例函数关系,图象如图所示.如果以此蓄电池为电源的电器的限制电流不能超过3A,那么电器的可变电阻R(Ω)应控制在( )
A.R≥1 B.0<R≤2 C.R≥2 D.0<R≤1
9.蓄电池的电压为定值,使用此电源时,用电器的电流I(A)与电阻R(Ω)之间的函数关系如图所示,如果以此蓄电池为电源的用电器限制电流不得超过9A,那么用电器的可变电阻应控制在( )范围内.
A.R≥4Ω B.R≤4Ω C.R≥9Ω D.R≤9Ω
10.如图,在某温度不变的条件下,通过一次又一次地对气缸顶部的活塞加压,测出每一次加压后气缸内气体的体积V(mL)与气体对气缸壁产生的压强P(kPa)的关系可以用如图所示的反比例函数图象进行表示,下列说法错误的是( )
A.气压P与体积V表达式为P,则k>0
B.当气压P=70时,体积V的取值范围为70<V<80
C.当体积V变为原来的时,对应的气压P变为原来的
D.当60≤V≤100时,气压P随着体积V的增大而减小
二、填空题
11.某厂计划建造一个容积为5×104m3的长方体蓄水池,则蓄水池的底面积S(m2)与其深度h(m)的函数关系式是 .
12.某高科技开发公司从2008年起开始投入技术改进资金,经过技术改进后,其产品的生产成本不断降低,具体数据如下表:请你认真分析表中数据,写出可以表示该变化规律的表达式是
年 度 2008 2009 2010 2011
投入技术改进资金x(万元) 2.5 3 4 4.5
产品成本y(万元∕件) 7.2 6 4.5 4
13.调查显示,某商场一款运动鞋的售价是销量的反比例函数(调查获得的部分数据如下表).
售价x(元/双) 200 240 250 400
销售量y(双) 30 25 24 15
已知该运动鞋的进价为180元/双,要使该款运动鞋每天的销售利润达到2400元,则其售价应定为 元.
14.面积一定的长方形,长为8时宽为5,当长为10时,宽为 .
15.某气球内充满了一定量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.则其函数解析式为 .
16.老王要把一篇24000字的社会调查报告录入电脑,则其录入的时间t(分)与录入文字的平均速度v(字/分)之间的函数表达式应为t= (v>0).
17.某物体对地面的压强p(N/m2)物体与地面的接触面积S(m2)之间的变化关系如图所示(双曲线的一支).如果该物体与地面的接触面积为0.24m2,那么该物体对地面的压强是 (N/m2).
18.在照明系统模拟控制电路实验中,研究人员发现光敏电阻值R(单位:Ω)与光照度E(单位:lx)之间成反比例函数关系,部分数据如下表所示:
光照度E/lx 0.5 1 1.5 2 2.5 3
光敏电阻阻值R/Ω 60 30 20 15 12 10
则光敏电阻值R与光照度E的函数表达式为 .
三、解答题
19.为了预防“甲型H1N1”,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
20.在压力不变的情况下,某物体所受到的压强p(Pa)与它的受力面积S(m2)之间成反比例函数关系,其图象如图所示.
(1)求p与S之间的函数表达式;
(2)当S=0.4m2时,求该物体所受到的压强p.
21.某种气球内充满了一定质量的气体.当温度不变时,气球内气体的压强P/(kPa)是气球体积V/(m3)的反比例函数,其图象如图所示.
(1)求这个反比例函数的表达式;
(2)当气球内气体的气压大于120 kPa时,气球将爆炸.为了安全起见,气球体积应该不小于多少立方米?
22.一辆货车和一辆轿车从南京出发,均沿沪宁高速公路匀速驶向目的地上海,已知沪宁高速公路全长约300km.设货车的速度是xkm/h,到达上海所用的时间为yh.
(1)写出y关于x的函数表达式;
(2)沪宁高速公路规定:货车的速度不得超过90km/h,求货车到达上海所需的最短时间;
(3)若轿车的速度是货车的1.5倍,轿车到达上海所用的时间比货车少1小时15分钟,求轿车的速度.
23.码头工人往一艘轮船上装载一批货物,每天装载30吨,8天装载完毕.
(1)轮船到达目的地后开始卸货,卸货速度v(吨/天)与卸货天数t之间有怎样的函数关系?
(2)由于遇到紧急情况,要求船上的货物5天之内卸载完毕,那么每天至少要卸货多少吨?
24.饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热,此过程中水温y(℃)与开机时间x(分)满足一次函数关系,当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系,当水温降至20℃时,饮水机又自动开始加热……,重复上述程序(如图所示),根据图中提供的信息,解答问题:
(1)当0≤x<8时,求水温y(℃)与开机时间x(分)的函数关系式.
(2)求图中t的值;
(3)若在通电开机后即外出散步,请你预测散步42分钟回到家时,饮水机内水的温度约为多少℃?
答案
一、选择题.
A.B.A.D.C.B.C.C.A.B.
二、填空题
11.S.
12.y.
13.300.
14.4.
15.P.
16..
17.500.
18.R.
三、解答题
19.(1)设药物燃烧时y关于x的函数关系式为y=k1x(k1>0),
代入(8,6)得6=8k1,
∴k1,
设药物燃烧后y关于x的函数关系式为y(k2>0),
代入(8,6)得
6,
∴k2=48,
∴药物燃烧时y关于x的函数关系式为(0≤x≤8)药物燃烧后y关于x的函数关系式为:
(x>8),
∴;
(2)把y=3代入,得:x=4,
把y=3代入,得:x=16,
∵16﹣4=12,
所以这次消毒是有效的.
20.(1)解:设 p(k≠0),
∵图象过点(0.1,1000)
∴1000
解得,k=100,
∴p与S之间的函数表达式是p;
(2)当S=0.4时,则 p250,
答:当S=0.4m2时,该物体所受到的压强p是250Pa.
21.(1)设P与V的函数关系式为P,
则60,
解得k=96,
∴函数关系式为P;
(2)当P>120KPa时,气球将爆炸,
∴P≤120,即120,
解得V≥0.8(m3).
故为了安全起见,气体的体积应不小于0.8(m3).
22.(1)设货车的速度是xkm/h,到达上海所用的时间为yh,根据题意可得:
xy=300,
故y;
(2)把x=90代入y,得y,
根据反比例函数的性质,当x>0时,y随x的增大而减小,
所以当x≤90km/h时,货车到达上海所需的最短时间为小时;
(3)根据题意可得:,
解方程得:x=80,
经检验得:x=80是原方程的解,且符合题意,
1.5x=120,
答:轿车的速度为120km/h.
23.(1)轮船上的货物总量为:30×8=240(吨),
故v关于t的函数表达式为v;
(2)把t=5代入v,得
v48,
∵t>0时,
∴v随t的增大而减小,
故船上的货物5天之内卸载完毕,每天至少要卸货48吨.
24.(1)当0≤x≤8时,设水温y(℃)与开机时间x(分)的函数关系式为y=kx+b(k≠0),
将(0,20)、(8,100)代入y=kx+b中,
,解得:,
∴当0≤x≤8时,水温y(℃)与开机时间x(分)的函数关系式为y=10x+20.
(2)当8≤x≤t时,设水温y(℃)与开机时间x(分)的函数关系式为y(m≠0),
将(8,100)代入y中,
100,解得:m=800,
∴当8≤x≤t时,水温y(℃)与开机时间x(分)的函数关系式为y.
当y20时,x=40,
∴图中t的值为40.
(3)∵42﹣40=2≤8,
∴当x=2时,y=2×10+20=40,
答:散步42分钟回到家时,饮水机内水的温度约为40℃.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
