1.1.2集合间的基本方法(浙江省杭州市西湖区)
文档属性
| 名称 | 1.1.2集合间的基本方法(浙江省杭州市西湖区) | 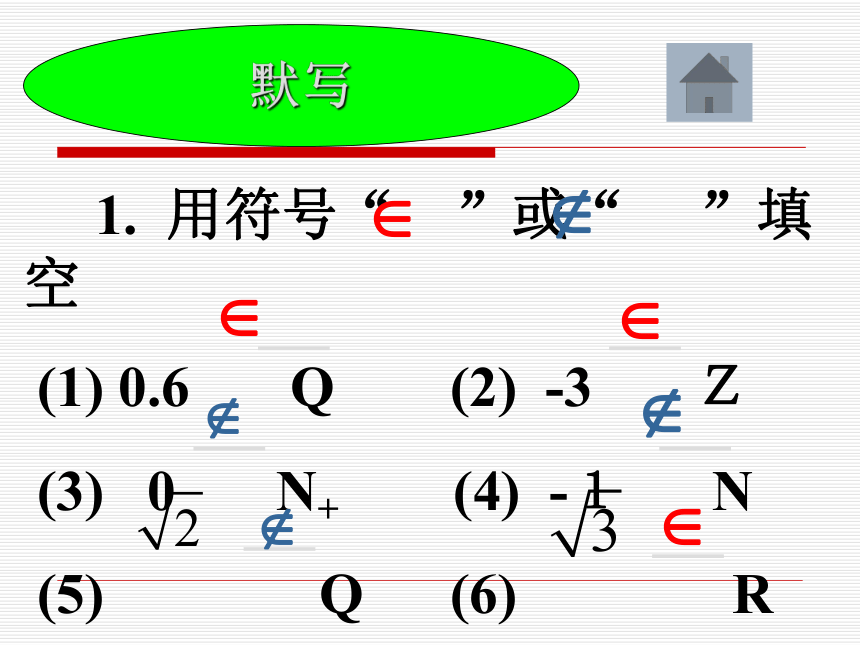 | |
| 格式 | rar | ||
| 文件大小 | 96.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-09-05 11:08:00 | ||
图片预览







文档简介
课件19张PPT。 1. 用符号“ ”或“ ”填空
(1) 0.6 Q (2) -3 Z
(3) 0 N+ (4) -1 N
(5) Q (6) R默写(7)若
0 A, 1.33 A选用合适的方法表示下列集合1由方程 的所有实数根组成的集合;
2由大于-5小于5的奇数组成的集合;
3不等式2x>3-x的解集;
4二次函数 的函数值组成的集合.
1.1.2集合间的基本关系思考:实数有相等关系,大小关系,如2=2,2<3,
3>2,4≤5等等,类比实数之间的关系,
你会想到集合之间的什么关系?观察下面的例子,你能发现两个集合之间的关系吗?(1) 设A={x|x是两条边相等的三角形},
B={x|x是等腰三角形}.
(2) A ={1,2,3},B={1,2,3,4,5};子集定义:自然语言:如果集合A中任意一个元素都是集合B中的元素,称集合A是集合B的子集.
符号语言: 读作“A含于B”(B包含A)
图形语言:
Venn图:用平面上封闭曲线的内部代表集合的图形.它可以是圆,椭圆,矩形等等.
A 1,2,3B
4,5集合的四种表示方法自然语言:大于0小于10的所有偶数的集合
列举法:
描述法:
Venn图法:
2,4,6,8从子集角度进一步理解“集合的相等” 设A={1,2},
B={1,2}. 真子集(2) A ={1,2,3},B={1,2,3,4,5};
自然语言:如果集合 ,但存在元素 称集合A是集合B的真子集.
符号语言: 读作“A真含于B”(B真包含A)
图形语言:
A1,2,3 B 4,5 ≠≠观察下面的例子,你能发现两个集合之间的关系吗?(1) 设A={x|x是两条边相等的三角形},
B={x|x是等腰三角形}.
(2) A ={1,2,3},B={1,2,3,4,5};集合与集合的关系有几种?子集,真子集,相等.BAA(B)若A是B的真子集则A一定是B的子集,
若A是B的子集,但A不一定是B的真子集.不含任何元素的集合叫做空集,记
规定:空集是任何集合的子集.
区别:0,{0},思考:如何用集合来表示方程 的实数根?例题1: 写出集合{a,b}的所有子集,并指出哪些是它的真子集.练习1具体写出集合{a,b,c} 的子集,真子集.思考:集合的性质用适当的符号填空:A(非空)AAACAC( ){x|x是平行四边形} {x|x是正方形}( = )小结集合的四种表示方法
集合与集合间的关系:子集,真子集,相等
集合的性质
空集
包含关系与属于关系的区别
(1) 0.6 Q (2) -3 Z
(3) 0 N+ (4) -1 N
(5) Q (6) R默写(7)若
0 A, 1.33 A选用合适的方法表示下列集合1由方程 的所有实数根组成的集合;
2由大于-5小于5的奇数组成的集合;
3不等式2x>3-x的解集;
4二次函数 的函数值组成的集合.
1.1.2集合间的基本关系思考:实数有相等关系,大小关系,如2=2,2<3,
3>2,4≤5等等,类比实数之间的关系,
你会想到集合之间的什么关系?观察下面的例子,你能发现两个集合之间的关系吗?(1) 设A={x|x是两条边相等的三角形},
B={x|x是等腰三角形}.
(2) A ={1,2,3},B={1,2,3,4,5};子集定义:自然语言:如果集合A中任意一个元素都是集合B中的元素,称集合A是集合B的子集.
符号语言: 读作“A含于B”(B包含A)
图形语言:
Venn图:用平面上封闭曲线的内部代表集合的图形.它可以是圆,椭圆,矩形等等.
A 1,2,3B
4,5集合的四种表示方法自然语言:大于0小于10的所有偶数的集合
列举法:
描述法:
Venn图法:
2,4,6,8从子集角度进一步理解“集合的相等” 设A={1,2},
B={1,2}. 真子集(2) A ={1,2,3},B={1,2,3,4,5};
自然语言:如果集合 ,但存在元素 称集合A是集合B的真子集.
符号语言: 读作“A真含于B”(B真包含A)
图形语言:
A1,2,3 B 4,5 ≠≠观察下面的例子,你能发现两个集合之间的关系吗?(1) 设A={x|x是两条边相等的三角形},
B={x|x是等腰三角形}.
(2) A ={1,2,3},B={1,2,3,4,5};集合与集合的关系有几种?子集,真子集,相等.BAA(B)若A是B的真子集则A一定是B的子集,
若A是B的子集,但A不一定是B的真子集.不含任何元素的集合叫做空集,记
规定:空集是任何集合的子集.
区别:0,{0},思考:如何用集合来表示方程 的实数根?例题1: 写出集合{a,b}的所有子集,并指出哪些是它的真子集.练习1具体写出集合{a,b,c} 的子集,真子集.思考:集合的性质用适当的符号填空:A(非空)AAACAC( ){x|x是平行四边形} {x|x是正方形}( = )小结集合的四种表示方法
集合与集合间的关系:子集,真子集,相等
集合的性质
空集
包含关系与属于关系的区别
