全等三角形的判定(SAS)(河南省洛阳市)
文档属性
| 名称 | 全等三角形的判定(SAS)(河南省洛阳市) |

|
|
| 格式 | rar | ||
| 文件大小 | 600.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-09-04 00:00:00 | ||
图片预览




文档简介
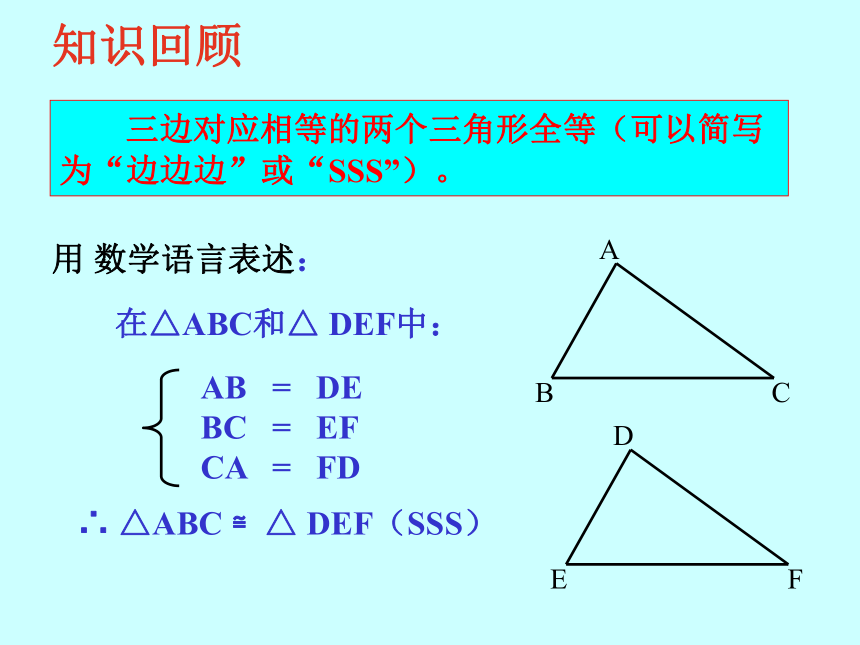
课件18张PPT。请 大 家 保 持 安 静 !祝同学们学习进步13.2探索三角形全等的判定(SAS)知识回顾 三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。用 数学语言表述:在△ABC和△ DEF中:∴ △ABC ≌△ DEF(SSS) AB = DE
BC = EF
CA = FD确定目标 合作探究1、两边和它们的夹角对应相等的两个三角形全等吗?(SAS)
2、两边和其中一边的对角对应相等的两个三角形全等吗?(SSA)
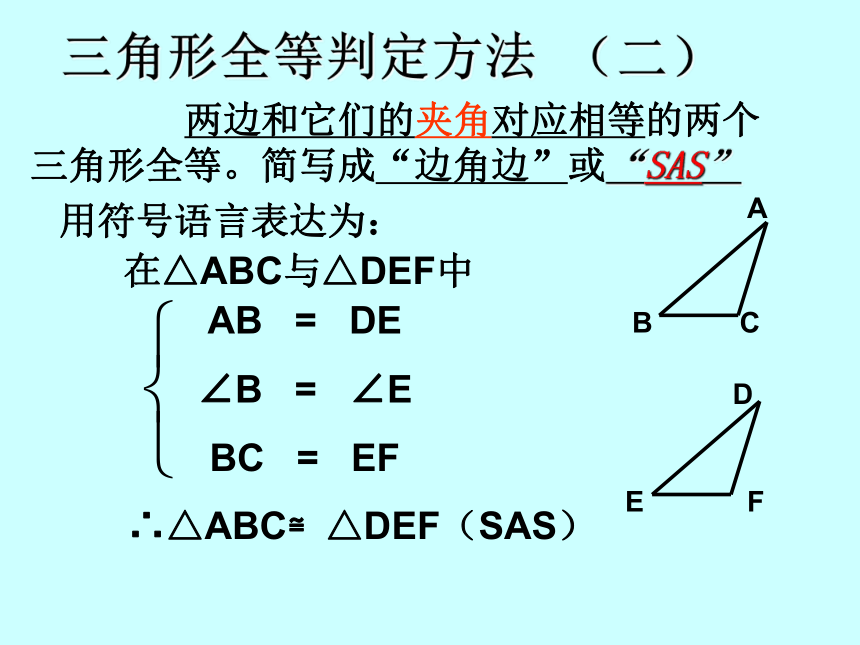
3、边角边(SAS)判定全等的步骤是什么?做一做:任意画△ABC,再画一个△A’B’C’使A’B’=AB,A’C’=AC ,∠A’= ∠A (即使两边和它们的夹角对应相等。把画出来的△A’B’C’剪下,放到△ABC上,它们全等吗? 画法:2. 在射线A’D上截取A’B’= AB3. 在射线A’E上截取A’C’=AC 1. 画∠DA’E= ∠A 4. 连接B’C’∴△A’B’C’就是所求的三角形比较结果:它们能 互相重合 。探究 1 三角形全等判定方法 (二)用符号语言表达为:在△ABC与△DEF中AB = DE
∠B = ∠E
BC = EF∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”
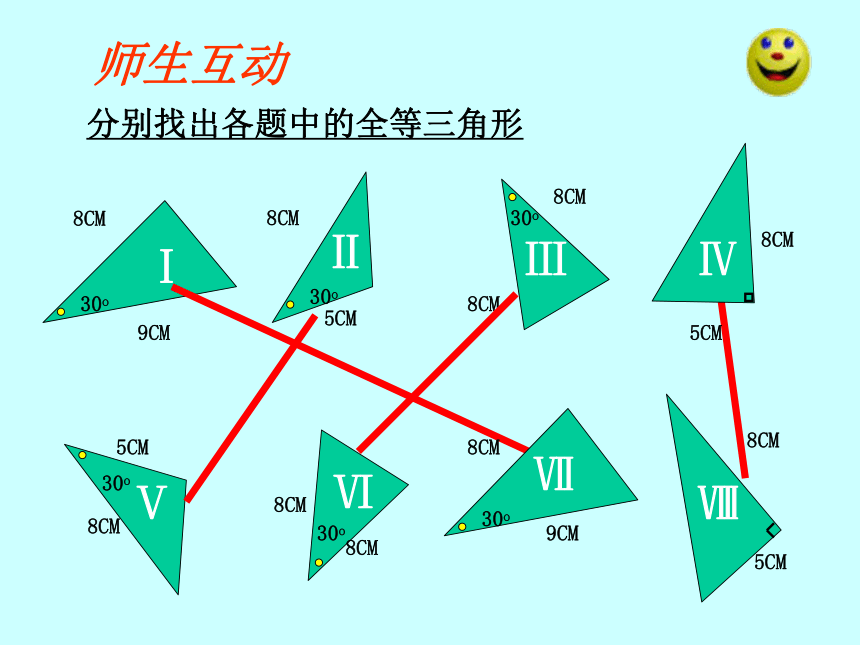
师生互动分别找出各题中的全等三角形已知:如图, AB=CB ,∠ABD=∠CBD
问:△ ABD 和△ CBD 全等吗?
分析:△ ABD ≌△ CBDAB=CB(已知)∠ABD= ∠CBD(已知)?ABCD检测:
1、 如图AC与BD相交于点O,已知OA=OC,OB=OD,说明△AOB≌△COD的理由。证明:在△ AOB 和 △ COD 中OA = OC
∠AOB = ∠COD
OB = OD
∴△AOB≌△COD(SAS)2、已知:如图, AD=CD ,∠ADB=∠CDB
求证: AB=CB , ∠ABD=∠CBD 。
ABCD归纳:判定两条线段相等或二个角相等可以通过从它们所在的两个三角形全等而得到。检测:证明:在△ ABD 和 △ CBD 中AD = CD
∠ADB = ∠CDB
BD = BD
∴△ABD≌△CBD(SAS)∴AB=CB, ∠ABD=∠CBD 理解新知 活学活用 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。请你设计一种方案,粗略测出A、B两杆之间的距离。。AB 小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。想一想 AC=DC?
∠ACB=∠DCE
BC=EC △ACB≌△DCE
AB=DE 若AB=AC则添加什么条件可得ΔABD≌ΔACDADBC∠BAD= ∠ CAD师生互动BD=CD 以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?ABCDEF2.5cm3.5cm40°40°3.5cm2.5cm结论:两边及其一边所对的角相等,两个三角形不一定全等探究2猜一猜:是不是二条边和一个角对应相等,这样的两个三角形一定全等吗?你能举例说明吗?如图△ABC与△ABD中,AB=AB,AC=AD, ∠B=∠B他们全等吗?注:“边角边(SAS)定理”中要求的这个角(A)一定是这两边所夹的角才行。课堂小结:1、 三角形全等的判定(二):
两边和它们的夹角对应相等的两个三角形全等 。简称 :边角边或 SAS。2、 判定两条线段相等或两个角相等可以通过证明它们所在的两个三角形全等来得到。A拓展延伸如图:在△AFD和△ CEB中,点A、E、F、C在同一直线上,有以下四个论断:
(1)AD=CB;(2)AE=CF;(3) ∠ B =∠ D;(4)AD∥BC。 请用其中三个作为条件,余下一个作为结论,编一道数学题,并写出规范的解答过程。作业P15、作业题 3、4。
BC = EF
CA = FD确定目标 合作探究1、两边和它们的夹角对应相等的两个三角形全等吗?(SAS)
2、两边和其中一边的对角对应相等的两个三角形全等吗?(SSA)
3、边角边(SAS)判定全等的步骤是什么?做一做:任意画△ABC,再画一个△A’B’C’使A’B’=AB,A’C’=AC ,∠A’= ∠A (即使两边和它们的夹角对应相等。把画出来的△A’B’C’剪下,放到△ABC上,它们全等吗? 画法:2. 在射线A’D上截取A’B’= AB3. 在射线A’E上截取A’C’=AC 1. 画∠DA’E= ∠A 4. 连接B’C’∴△A’B’C’就是所求的三角形比较结果:它们能 互相重合 。探究 1 三角形全等判定方法 (二)用符号语言表达为:在△ABC与△DEF中AB = DE
∠B = ∠E
BC = EF∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”
师生互动分别找出各题中的全等三角形已知:如图, AB=CB ,∠ABD=∠CBD
问:△ ABD 和△ CBD 全等吗?
分析:△ ABD ≌△ CBDAB=CB(已知)∠ABD= ∠CBD(已知)?ABCD检测:
1、 如图AC与BD相交于点O,已知OA=OC,OB=OD,说明△AOB≌△COD的理由。证明:在△ AOB 和 △ COD 中OA = OC
∠AOB = ∠COD
OB = OD
∴△AOB≌△COD(SAS)2、已知:如图, AD=CD ,∠ADB=∠CDB
求证: AB=CB , ∠ABD=∠CBD 。
ABCD归纳:判定两条线段相等或二个角相等可以通过从它们所在的两个三角形全等而得到。检测:证明:在△ ABD 和 △ CBD 中AD = CD
∠ADB = ∠CDB
BD = BD
∴△ABD≌△CBD(SAS)∴AB=CB, ∠ABD=∠CBD 理解新知 活学活用 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。请你设计一种方案,粗略测出A、B两杆之间的距离。。AB 小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。想一想 AC=DC?
∠ACB=∠DCE
BC=EC △ACB≌△DCE
AB=DE 若AB=AC则添加什么条件可得ΔABD≌ΔACDADBC∠BAD= ∠ CAD师生互动BD=CD 以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?ABCDEF2.5cm3.5cm40°40°3.5cm2.5cm结论:两边及其一边所对的角相等,两个三角形不一定全等探究2猜一猜:是不是二条边和一个角对应相等,这样的两个三角形一定全等吗?你能举例说明吗?如图△ABC与△ABD中,AB=AB,AC=AD, ∠B=∠B他们全等吗?注:“边角边(SAS)定理”中要求的这个角(A)一定是这两边所夹的角才行。课堂小结:1、 三角形全等的判定(二):
两边和它们的夹角对应相等的两个三角形全等 。简称 :边角边或 SAS。2、 判定两条线段相等或两个角相等可以通过证明它们所在的两个三角形全等来得到。A拓展延伸如图:在△AFD和△ CEB中,点A、E、F、C在同一直线上,有以下四个论断:
(1)AD=CB;(2)AE=CF;(3) ∠ B =∠ D;(4)AD∥BC。 请用其中三个作为条件,余下一个作为结论,编一道数学题,并写出规范的解答过程。作业P15、作业题 3、4。
